邻频干扰对跳频系统中断概率的影响研究

李梓宁

（长讯通信服务有限公司）

邻频干扰对跳频系统中断概率的影响研究

李梓宁

（长讯通信服务有限公司）

本文以跳频系统中的某个特定通信频点为切入点，对该通信频点的邻频干扰功率进行假设，并以此为前提，进行邻频干扰对跳频系统中断概率的影响研究。并通过对接收端SINR的分布函数的分析，得出以可用频点数、干扰台站数以及信道参数为变量的中断概率公式，并进行仿真验证，以期能为台站布置及跳频系统的性能分析提供参考。

邻频干扰；跳频系统；中断概率；影响研究

1 引言

通信站台布置在同一区域内会相互产生干扰，如何依据已知的系统配置，对系统性能的影响，是当前系统配置中必须解决的问题。国内外学者主要从接收端干扰信号的特征函数和联合概率密度函数分析接收端的信干噪比（Signal－to－Interference－and－NoiseRatio，SINR），得到误码率、传输容量以及中断概率等性能指标。如果服从空间泊松对干扰台站进行分布，从能量层与信号层两个角度分析干扰信号的特征函数，得到接收端干扰功率服从S（α，β，γ）偏正态分布的结论，并将其应用于通信系统、分组交换网、AdHoc网中。在上述研究的基础上，针对蜂窝通信系统，假定干扰台站分布于圆环区域内分布，得到中断概率的上、下限。上述研究都是基于系统内通信台站服从某一分布的假设上展开并取得的结论，并没有对系统内通信台站服从于任意位置的情况进行考虑。以联合概率密度函数为切入点，对处于不同位置上的干扰站台进行分析，即空间泊松分布、均匀分布以及位置固定，跳频系统受邻频干扰影响的传输容量与中断概率。通过频表规划，传跳频系统，有效减小了同频干扰，但基于对用频效率的考虑，邻频干扰在一定程度上仍然存在。因此，本文中对邻频干扰对跳频系统中段概率的影响研究具有很强的现实意义。

2 系统模型

2．1 系统布置

如图1所示，为典型的美国陆军超短波跳频系统应用场景，接收方R0在周边布置多个通信台站i={1，2，…，M}，其中M所代表的是通信台站在区域内总和。接收远端在向外进行信号发射时，很容易受附近台站信号发射的邻频干扰。

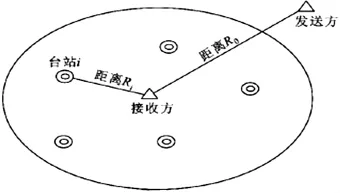
图1 系统配置

以接收方所在位置为原点，建立极坐标系，Ri为接收方与第i个干扰台站的间距，R0为通信距离，各台站在进行通信过程中，必须始终维持在固定的位置上。干扰台站i频谱发射的邻频功率为Pi，i={1，2，…，M}，信号功率为P0。邻频干扰概率为：

F为区域整体所分配的可用频点数。基于对频表计划所产生的邻频干扰概率增益的考虑，式（1）还可以表现为：

其中，G所代表的就是利用频表规划所可能增长的邻频干扰概率。

2.2 信道模型

信道的功能主要体现在小尺度衰落、阴影衰落以及路径损耗上，利用信道的作用，接收端与干扰台站i之间功率为：

εi～N（0，σ）为第i条信道的阴影衰落因子。n为路径损耗指数，通常在3～8范围内；gi=α2i且E[gi]=1，αi为小尺度衰落因子。因为αi的分布遵循Nakagami-m，所以gi也需遵循进行分布，中段概率中反映密度的函数为：

其中假定mi在一个符号周期内保持不变。其所表示的就是第i条信道上的Nakagami参数。

2.3 接收端信干噪比

接收端干扰功率与信号功率之间的比率即为接收端信干噪比，以公式来说明就是：

3 系统中断概率

跳频通信系统中断概率具体就是指出现某一中段门限高于接收端SINR的概率，以公式进行表现就是：

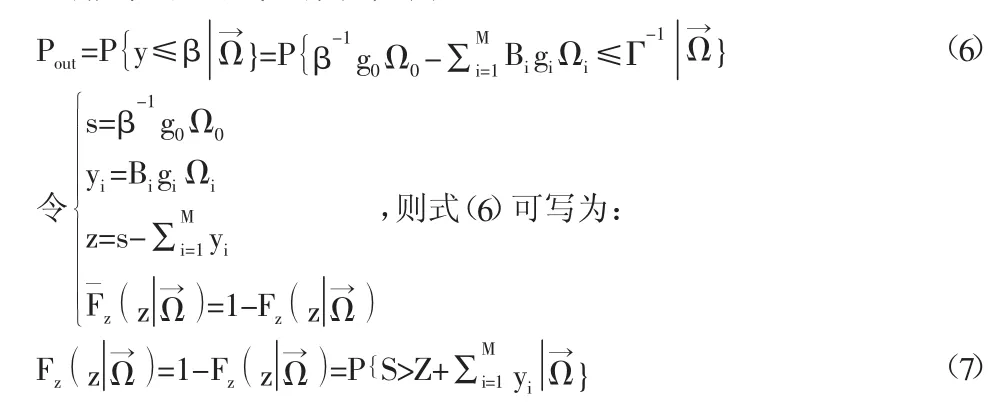
其中，fyy→（）为接收端干扰功率的联合概率密度函数为接收端信号功率的概率密度函数。结合上式（4）可求出s的概率密度函数的公式为｝。其中，M为干扰台站数，mi，i={0，1，…M}为对应的信道参数，其他参数为中间变量。

4 仿真结果

以美陆军超短波频段中55MHz的频点作为对象，对上述中断概率公式是否正确进行验证。跳频系统中断概率的仿真模拟，应当在充分考虑到多种条件下的Nak-agami可用频点数、台站数量和信道参数的基础上进行。仿真实验进行100000次。首先，对仿真实验中所需的3个仿真参数进行确定：信噪比在-5～25dB范围内转换，干扰台站发射频谱的邻频功率Pi=-20dBm，i={1，2，…，M}，噪声功率N=-30dBm。干扰台站均匀的分布于2～8km范围内，通信双方之间的距离为10km，中断门限β=0dB，邻频干扰概率增益G=1。结果详情可见图2～4。

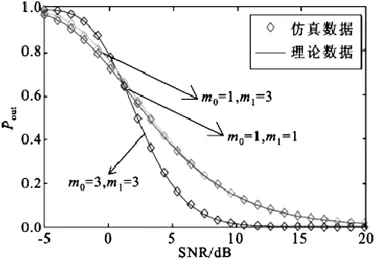
图2 pa=1、M=4时，Pout与SNR关系Fig

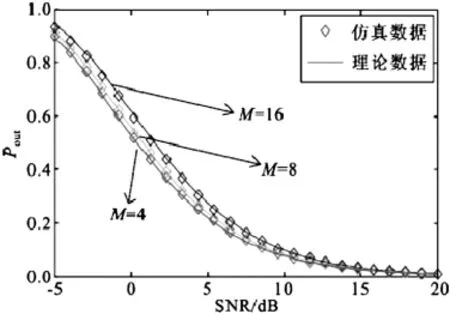
图3 F=10、m0=1、mi=3时，Pout与SNR关系

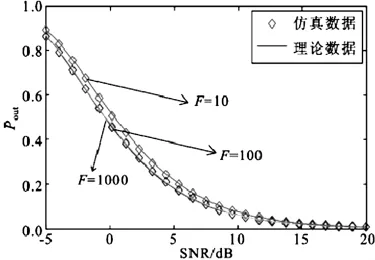
图4 M=4、m0=1、mi=3时，Pout与SNR关系

利用Rice因子与KNakagami信道参数m之间的关系m=（K+1）22K+1（20），表明m在某种层面上来讲直接表示的是直射路径的能量，也就是Nakagami信道中K0=4.5，Ki=4.5，i={1，2，…，M}，混合信道中K0= 0，Ki=4.5，i={1，2，…，M}和Rayleigh信道中K0=0，Ki=0，i={1，2，…，M}。对图2进行分析，可以得出：当SNR较大时，Nakagami信道与对比混合信道相比，后者由于通信信道没有直射能量存在，相较于Nakagami信道中断概率更小；当SNR较小时，Rayleigh信道与对比混合信道相比较，后者由于干扰信道中有直射能量存在，相较于Rayleigh信道，中断概率也会更大；但随着SNR的不断升高，中断概率受台站干扰的程度越来越低，Nakagami信道、对比混合信道、Rayleigh信道三者的中断概率也会逐步趋于0。为使试验更加简单与便捷，实验3和4中，使4个干扰信道的均在同样的信道状态下（混合信道条件）进行。如图3所示：可用频点数与信道参数在相同的状态下，如果SNR较小时，影响中段概率吧的主要因素就在于干扰能量，如果干扰台站数越多，其中断概率也会随之增大。但随着SNR的不断升高，中断概率受台站干扰的程度越来越低，Nakagami信道、对比混合信道、Rayleigh信道三者的中断概率也会逐步趋于0。图4表明：干扰台站数与信道状态相同的情况下，依照干扰频数与可用频点数的联系，中断概率变小，可用频点数增多；但邻频干扰概率与可用频点数之间呈类反比关系。但如果可用频点数越来越多，中断概率变化也会越来越小，邻频干扰概率也越小。

5 结束语

综上，文章中以跳频通信中的某一通信频点，针对邻频干扰对跳频系统中断概率的影响，在干扰台站布置已知的基础上，进行仿真实验，并得出跳频系统中断概率的计算式，并就跳频系统中的可用频点数、干扰台站数及信道参数等重要参数进行科学计算。理论和仿真结果表明：信道参数与干扰台站数对于跳频系统中断概率之间存在着密切的关联，有效证实了理论的正确性，为跳频系统的性能分析和不同信道条件下的台站布置提供了指导。

[1]VALENTI M C，TORRIERI D，TALARICO S.A Direct Approach to Computing Spatially Averaged Outage Probability[J].IEEE CommunicationsLetters，2014，18（7）：1103～1106.

[2]寇治刚.跳频通信系统干扰技术研究与仿真[J].通信技术，2012，16（5）：43～44.

[3]赵诗琴，杜荣，李剑，李生红.基于干扰建模的通信中断概率分析[J].计算机工程，2013（07）.

TN914.41

A

1004-7344（2016）24-0274-02

2016-8-8