基于频率分解及倾斜叠加法的面波频散曲线提取方法

■徐维

（甘肃煤田地质局一四九队甘肃兰州730020）

基于频率分解及倾斜叠加法的面波频散曲线提取方法

■徐维

（甘肃煤田地质局一四九队甘肃兰州730020）

面波有着衰减小、信噪比高、抗干扰能力强以及在层状介质中具有频散特性的优点在浅层勘探中得以广泛应用。面波频散曲线在反演浅层地下结构、工程地质勘察、地下空间及掩埋物的探测、无损检测等领域有着至关重要的作用。如何提取准确可靠的频散曲线是瑞利波勘探应用中的关键问题之一，传统的面波频散曲线提取方法主要是利用傅里叶变换，得到两信号的自功率谱、互功率谱、传递函数和相干函数，由互功率谱可以得到两信号由于波传播过程中的时间滞后所产生的相位差，进而求得实测的频散曲线。本文主要介绍了频率分解与倾斜叠加法提取面波频散曲线的方法、特点及实例应用。

面波 频散曲线 频率分解 倾斜叠加

1　基本原理

设x(d，t)为d～t域的多道地震数据，其中d为偏移距（震源和接收器间的距离）。首先通过频率分解将x（d，t）（Coruh，1985）转换成X(d，t)。X(d，t)为伪震源数据或扫频数据。公式如下：

其中，X是卷积操作，S（t）是一定频率范围内的一个线性或非线性扫描。卷积计算多用FFT法。GOUPILLAUD（1976）给出了S(t)的一般形式：

其中f(t)为瞬时频率，它确定了时间和频率之间的一对一的关系。只要瑞利波的频带在扫描的频带范围内，就可以对任何扫描进行频率分解。因为线性扫描具有简单性（时间和频率之间的线性关系）和均一性（‘box card’频谱）的优点，所以在做频率分解时，我们通常选择线性扫描。频谱分析可以确定瑞利波的频带，从而可以设置优于频率分解的扫描的频带。在频率分解（公式(1)）后便将数据由时间向频率转换。如果最初的数据为可控震源数据，那么这种分解过程就可以省略。

在一个预定的相速度范围内，对X（d，t）倾斜叠加。关于倾斜叠加的讨论见YILMAZ(1987,p.430)。这里只列出算法中用到的相关方程。第一步，通过坐标转换对进行线性动校正（CLAERBOUT，1978年），即：

第二步，对进行线性动校正后，以的1/v进行平滑，并在炮检距的轴对获得数据求和，得：

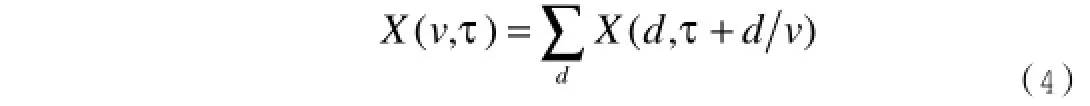
2　理论模型

我们利用一个三层介质模型，具体模型参数如图1，图2(左)为上述理论模型面波合成记录。具体参数为60道接收，采样率为400μs，炮检距1m，道间距1m。

利用上述方法对该理论数据进行处理，我们得到如图2(右)所示的f～v图，从图中可以看出提取的横波速度与图1理论模型中的速度接近，验证了该算法及其实现的正确性。

3　实际应用

如图3(左)所示，为某地野外实测记录，施工参数为：采样率0.25ms，炮检距1m，道间距1m，24道的接收。对该数据提取频散曲线得到图3(右)。

从图3(右)中可以看出，频率分解与倾斜叠加法所提取的频谱能够分离低频和高频部分，且其分辨率很高。

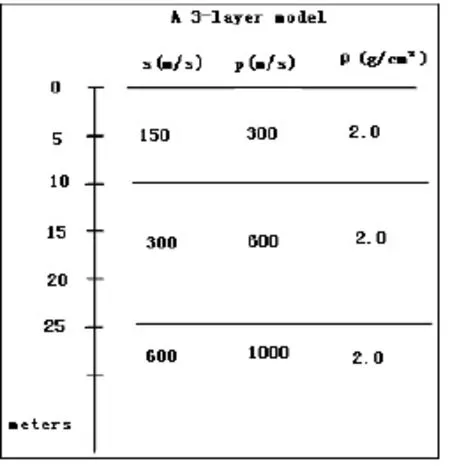
图1　理论模型及参数

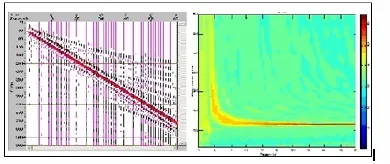
图2　理论模型合成面波记录(左)及处理后f～v图(右)

图3　实测记录(左)与处理后f～v图

4　结论及存在问题

通过以上理论验证及实际应用效果，充分验证了该方法的正确性，其最大特点为算法只用到了炮间距这唯一的信息，所以对于任意采集观测系统所采集到的数据都可以利用该算法提取频散曲线；其次该算法简单、明了，且对于对于基阶和高阶的面波，均能提取很好的频散曲线。

在实践过程中发现利用频率分解与倾斜叠加法提取频散曲线时，当各种转换波与面波严重耦合在一起时，难以选择最佳的观测窗口；由于时间有限，对该方法的算法的实现优化程度有待进一步完善，有些细节还需完善。

[1]秦臻，姚姚，张才，宋建勇，频率域速度谱中提取面波的多模频散曲线方法.人民长江,2009.40(11):1001～1013.

[2]鲁来玉，张碧星，汪承灏，基于瑞利波高阶模式反演的实验研究.地球物理学报. 2006.49(4):1082～1091.

P624文献码]B

1000～405X（2016）～4～323～1