同轴圆筒流变仪初始瞬态黏度的解析与数值研究

徐睿妤，刘　刚，陈　雷，滕厚兴，卢兴国，许继凯

（中国石油大学（华东）储运与建筑工程学院，山东 青岛 266580）



同轴圆筒流变仪初始瞬态黏度的解析与数值研究

徐睿妤，刘刚，陈雷，滕厚兴，卢兴国，许继凯

（中国石油大学（华东）储运与建筑工程学院，山东 青岛 266580）

同轴圆筒流变仪在恒剪速或恒应力测试初始过程中测试黏度远高于真实值的现象与流场非稳态作用等因素有关。测量间隙内的Couette流动研究主要集中在边界条件为恒值或某一具体时间函数下的理论推导，而测量间隙的边界条件实际为某一动边界。假设动边界为任意f（t），将同轴圆筒间Newtonian流体初始流变测试过程简化为无限大平板间Couette流动，采用特征函数法和Laplace变换推导应力和剪速边界下流场及表观黏度精确解，同时依据不同间隙尺寸和运动黏度对6种边界条件下的瞬态表观黏度进行数值计算。结果表明：当υ ＜20 mm2·s-1时，控制剪速边界下流场及表观黏度平衡时间更短；当20 mm2·s-1＜υ＜20000 mm2·s-1时，控制应力边界下流场及表观黏度平衡时间更短；当υ ＞20000 mm2·s-1时，两类边界条件下的平衡时间相近。

黏度；流体动力学；数值分析；同轴圆筒流变仪；Couette流动；动边界函数；特征函数法

DOI：10.11949/j.issn.0438-1157.20150865

引　言

旋转流变仪作为流变测量的重要工具，其准确测量将为工业及科研领域的物料流变性研究提供一系列可靠的基础数据。然而，在流变仪转子由静止逐步达到设定转速或扭矩的瞬态过程中流场非稳态与仪器机械性能的综合作用导致牛顿流体测试黏度远高于真实值。启动初始，转子加速的机械反馈调节复杂，使得流变仪加载应力或剪速的有效值低于设定值，实际边界条件形式不便描述，边界条件的动态变化最终也体现为流场非稳态。若待测介质为牛顿流体，可待数据稳定后再进行采集；若待测介质为非牛顿流体（如黏弹性和触变性流体），则其流变性对加载条件与剪切历史极为敏感，数据采集应从测量夹具旋转开始，初始非稳态数据失真将直接影响研究者对物料属性的判断。

旋转流变测量即建立测量间隙内流场的边界测量值与流变参数间的力学响应，测量间隙内介质的初始流动过程类似于平板拖动或旋转体系下的Couette流动。已有诸多学者开展了瞬态Couette流动的理论与实验研究。针对平板拖动Couette流动（一板运动、一板静止），学者们推导了不同运动边界下的流场解析解。如Erdoǧan等［1-4］求解了恒速边界下的瞬态流场，Papanastasiou等［5］求解了振荡速度u（t）=u0cos（ωt）边界下的瞬态流场。针对旋转体系Couette流动，平行平板［6-8］、同轴圆筒体系［9］研究的边界条件亦包括恒角速度边界、振荡速度边界等［10］。Parter等［11］和Rajagopal［12］进一步在平行平板体系下考虑了黏性不可压缩流体以相同角速度绕不同轴旋转的不对称流场分布，Lai等［13］和Daniel［14］依据其理论开展了数值验证。除此之外，为增加工程适用性，一些学者考虑了加载外力、摩损、压降等外部因素对旋转体系的瞬态流场影响。Seth等［15］在平板旋转体系中加载横向电磁场，求解了黏性电导不可压缩流体的非稳态流动；Daniel［14］和Sheikholeslami等［16］则分别对平行平板中上板具有摩擦损耗的恒速度边界进行了解析与数值求解；Danish等［17］考虑恒蒸发损耗率和恒压降梯度，求解了受上板转速U（t）驱动的旋转平板间瞬态流场。尽管Couette流动的解析研究众多，但针对旋转流变仪边界、几何规格、测试结果建立流动参数与“瞬态黏度值”的研究尚不多见。

事实上，理论分析的模型均为无限大平板或无限长同轴圆筒，无限大空间尺寸导致流场最终达到均一而非稳态。Varsakelis等［18］采用Chebyshev多项式法求解并分析特征问题，通过线性稳定性分析研究单向非稳态Couette流动的稳定性，证明了流动始终非稳态，但由于流场变化的增长率很小而导致辨别非稳态十分困难。尽管如此，数值计算在一定的精度范围内仍可视其为稳态值。

除了流变仪测量间隙内流场本身的非稳态外，流变仪启动过程中转子系统的启动加速、机械惯性和反馈调节也会导致流场边界条件动态变化。Ravey等［19-21］指出，惯性空气轴承式黏度计的剪速或扭矩均非直接加载于转子，在电磁场一定时转子有效扭矩取决于转子瞬时角速度，转子需经历静止到设定值的加速过程，并不能瞬间达到预设值。Gleissle［22］在研究仪器非稳态机械特征时也指出，在控制剪速条件下测试黏弹性流体黏度时，若忽略剪切速率加速至预设值的阶段将导致黏度计算结果出现明显错误，其测试高分子硅油的表观黏度与稳态黏度关系得到了Hua［23］和Borg等［24］的认可。可见，有必要对旋转流变仪内初始瞬态过程做进一步研究。

因此，考虑已有研究的边界条件与旋转流变仪实际边界条件的差距，本研究假设控制应力及控制剪速边界条件为任意f（t），将同轴圆筒流变仪测量间隙内的瞬态流动简化为无限大平行平板间的Couette流动，忽略重力作用，进行理论模型解析求解。同时，采用两种间隙尺寸和不同运动黏度对不同边界条件下的初始表观黏度进行数值计算。

1　数学描述及其精确解

旋转流变仪同轴圆筒测量系统的测量间隙相对于转子长度非常小（比值约1%），若忽略转子端部效应，则间隙内的流动可简化为两无限长同轴圆筒间的流动。测量间隙的边界包括动边界与静边界，动边界在初始过程由静止逐步达到稳定，流场也由静止逐步发展并趋于稳定。根据同轴圆筒内流场的轴对称性，进一步将模型简化为流场沿径向变化的一维瞬态模型，即两无限大平板间的Couette流动，如图1（a）和图1（b）所示。化简平板间牛顿流体的NS方程，可得控制方程为

旋转流变仪可实现控制应力加载或控制剪速加载，常用加载方式为恒应力或恒剪速加载。根据流变仪厂家空载试验的经验值，采用恒应力加载模式时转子达到设定应力需5～10 ms，采用恒剪速加载模式时转子达到设定剪速需30～50 ms。由于与机械响应有关，施加的应力或剪速随时间动态变化并趋于稳定，因而将边界条件设为与时间有关的动边界条件。

1.1控制应力边界加载

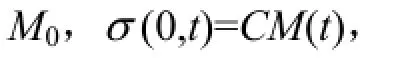
边界条件：移动边界处σ（0，t）= μ （∂u/∂x）|x=0，其剪切速率随时间变化，（∂u/∂x）|x=0=f（t）；固定边界处速度始终为0，u（d，t）=0。

初始条件：平板间隙内流体初始速度全部为0，u（x，t）=0（0≤x≤d）。该问题数学描述为

求解式（2）问题时，通过构造辅助函数将具有非齐次边界条件的齐次方程转化为具有齐次边界的非齐次泛定方程。u（x，t）=v（x，t）+w（x，t）为辅助函数，w（x，t）=f（t）（x-d），采用特征函数法及Laplace变换求解可得速度分布，如式（3）所示

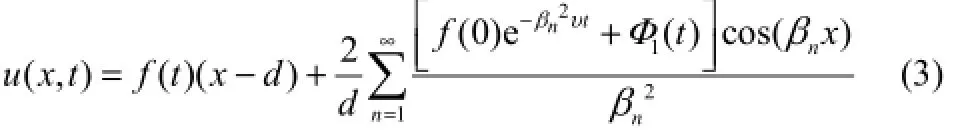
其中

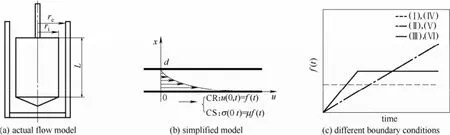
图1　实际及模型简图、边界函数形式Fig .1　Actual and simplified models and different boundary conditions

上述u（x，t）表达式中包含边界剪速函数的导数f′（t）。若f（t）在整个初始过程内连续可导，则上述公式适用；若f（t）在初始过程存在不可导点，如f（t）在转子自平衡时间t0内由0线性增加到设定值，此后保持设定值不变，t0为不可导点［如图1（c）中边界（Ⅲ）和（Ⅵ）］，则仍需进一步推导。

取t0为新的时间起点，计算t＞t0的速度分布。x=0处边界条件为（∂u/∂x）|x=0=σ0/μ，初始条件为u（x，0）= u（x，t0）。同样运用边界条件齐次化和固有函数法，可得t＞0（t0为时间起点）速度分布。利用t=t-t0统一时间起点，得整个初始过程的速度分布，如式（4）所示

其中

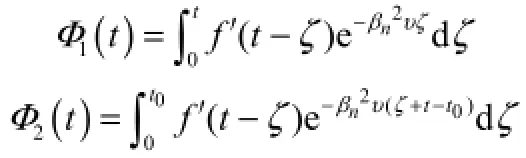
式中，f′（t-ζ）始终指t≤t0时的导数。

测试黏度为

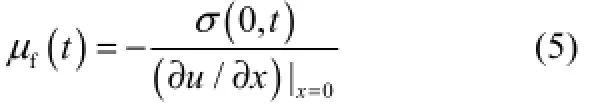
故理论相对黏度系数为

1.2控制剪速边界加载

流变仪控制剪速加载通过控制转速实现，σ ∝n。初始启动过程中，转速n由0逐渐增长至设定值n0，故u（0，t）=2πrn=f（t）。设t0为转子自平衡时间，即达到设定剪速值的时间，当t＞t0时u（0，t）=u0。

边界条件：移动边界处u（0，t）=f（t）；固定边界处速度始终为0，u（d，t）=0。

初始条件：平板间隙内流体初始速度全部为0，u（0，t）=0 （0≤x≤d）。

该问题的数学描述为

假设内边界上f（t）在t0处存在不可导点，采用如同1.1节的处理可得该加载方式下的速度分布，如式（8）所示。

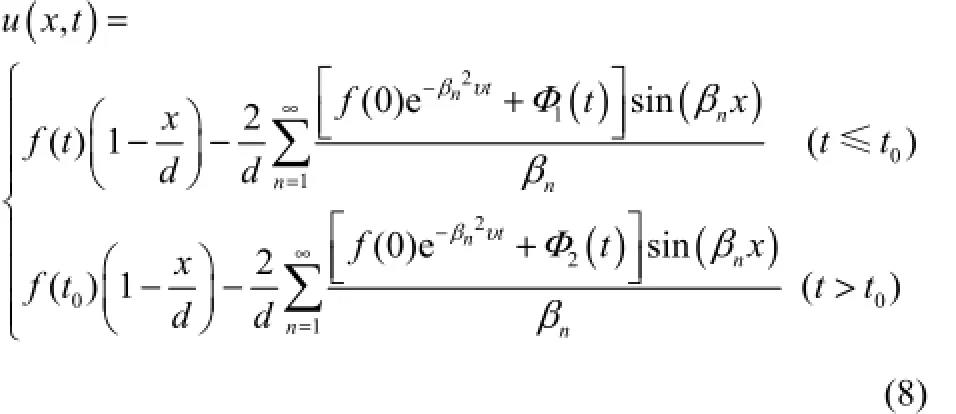
其中

理论黏度为

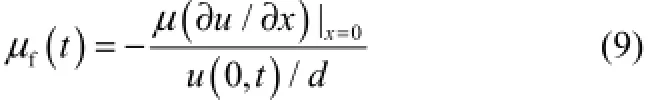
1.36种边界条件下相对黏度系数

根据控制应力和控制剪速在任意边界条件f（t）下的Couette解析解推导了6种特殊边界函数f（t）下的相对黏度系数ϕ。控制应力下的3种边界：（Ⅰ）恒应力；（Ⅱ）应力由0线性增加；（Ⅲ）应力由0线性增加至设定值后保持恒定。控制剪速下的3种边界：（Ⅳ）恒速度；（Ⅴ）速度由0线性增加；（Ⅵ）速度由0线性增加至设定值后保持恒定。

边界函数的形式如图1（c）所示。6种边界下的相对黏度系数见表1。ϕ趋近于1，表明瞬态过程逐步趋于稳态，表观黏度μf越接近牛顿流体的真实黏度μ。

表1　R6种边界条件下的相对黏度系数ϕTable 1　Relative viscosity coefficient ϕ under six kinds of boundary conditions

2　数值计算

根据（Ⅰ）～（Ⅵ）边界条件下相对黏度系数的解析解编制Matlab程序，对初始瞬态过程进行数值计算。空间尺度采用d=0.712 mm和d=1.136 mm两种规格；时间尺度取0～T；牛顿流体运动黏度选取2～200000 mm2·s-1。在计算域（0～d，0～T）内设置时空节点完成区域离散。

2.1转子自平衡时间处的“流场趋势变化”

图2　6种边界条件下ϕ随t的变化Fig. 2　Variation of ϕ with t under six boundary conditions υ=1000 mm2·s-1，d= 0.712 mm

为了分析不同边界条件下的瞬态黏度变化，分别模拟了6种边界条件下（d= 0.712 mm，υ = 1000 mm2·s-1）的ϕ=μf/μ随时间的变化（图2）和边界条件（Ⅲ）下测试不同黏度标准黏度液的ϕτic随时间的变化（图3）。当边界条件为（Ⅲ）时，参考MCR 102达到设定应力的实际时间为5～10 ms，取t0=10 ms；当边界条件为（Ⅵ）时，参考MCR 102达到设定剪速的实际时间为30～50 ms，取t0=50 ms。

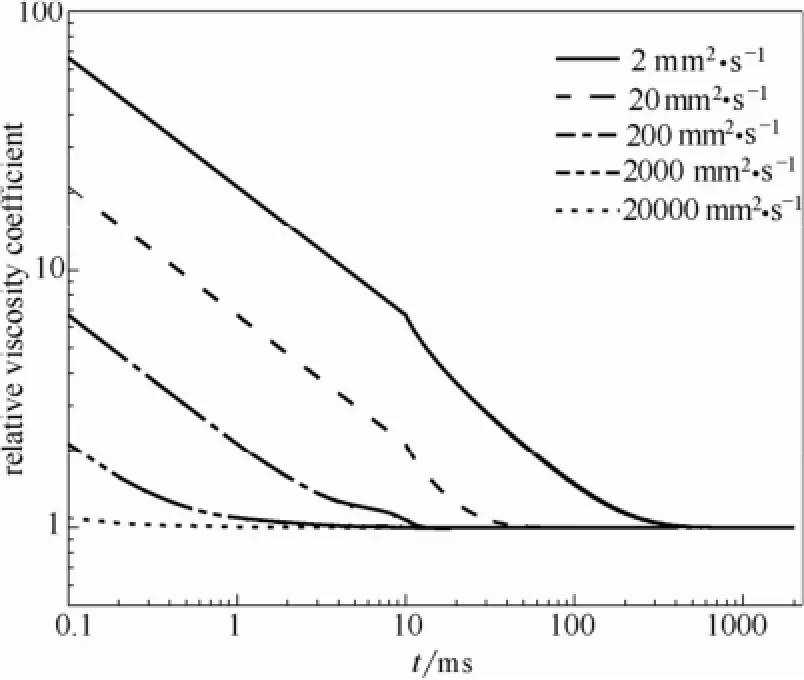
图3　不同运动黏度下ϕτic随t的变化Fig.3　Variation of ϕτicwith t under six boundary conditions υ=2—20000 mm2·s-1，d=0.712 mm，Ⅲ

2.2介质真实黏度、加载边界、测量间隙对瞬态平

衡时间的影响

采用运动黏度υ =2～200000 mm2·s-1和两种间隙尺寸计算（Ⅰ）～（Ⅵ）6种边界条件下的相对黏度平衡时间，如图4所示。相对黏度系数的平衡时间检出时，认为|ϕ （t）-1|＜0.1%时流场达到稳态，取td=t。

由图4可知，运动黏度增大时不同加载边界及测量间隙下的黏度平衡时间迅速减小，这是因为黏度大的流体层间内摩擦力增大，动边界的剪切传递效果得到强化，故而黏度平衡时间短。另外，不同测量间隙内流场的平衡时间不同，测量间隙越小，平衡时间越短，表观黏度将更快地接近真实值，这是因为剪切传递速度相同时测量间隙小的系统内的黏度平衡更快。在6种加载边界中，若计算时间足够长，则（Ⅰ）、（Ⅲ）、（Ⅳ）、（Ⅵ）4种边界下的表观黏度可达到其真实值，而（Ⅱ）、（Ⅴ）边界下的流场由于边界加载随时间线性增加，将始终不能达到真正的稳态，仅能达到流场均一化，ϕ （t）将趋近于1并大于1。因此，在控制应力边界和控制剪速边界中，分段边界下的黏度平衡过程均体现为恒定边界和线性增加边界下平衡过程的过渡。

在控制应力边界条件下，当υ＞200 mm2·s-1时，黏度平衡时间略滞后于转子自平衡时间（10 ms）；当υ＜100 mm2·s-1时，流场平衡过程趋近于（Ⅰ）恒应力或（Ⅳ）恒剪速边界下的平衡过程；当υ＞5000 mm2·s-1时，流场平衡过程趋近于（Ⅱ）应力线性增加或（Ⅴ）速度线性增加边界下的平衡过程。在控制剪速边界条件下，当υ＞20 mm2·s-1时，黏度平衡时间略滞后于转子自平衡时间（50 ms）；υ＜20 mm2·s-1时，流场平衡过程趋近于（Ⅰ）恒应力或（Ⅳ）恒剪速边界下的平衡过程；υ＞1000 mm2·s-1时，流场平衡过程趋近于（Ⅱ）应力线性增加或（Ⅴ）速度线性增加边界下的平衡过程。

图4　6种边界下不同运动黏度的牛顿流体平衡时间Fig. 4　Balance time of Newton fluid with different viscosity under six kinds of boundary conditions

图5　不同边界下不同运动黏度流体的平衡时间Fig. 5　Balance time of Newton fluid with different viscosity under different boundary conditions

两种测量间隙内6种边界条件下的表观黏度平衡如图5所示。在同一测量系统间隙下比较不同的6种边界条件下的相对黏度平衡时间，可知（Ⅱ）≈（Ⅴ）＞（Ⅰ）＞（Ⅳ）。当υ处于20～20000 mm2·s-1范围内时，6种边界条件下表观黏度平衡时间的关系为：（Ⅱ）≈（Ⅴ）＞（Ⅵ）＞（Ⅲ）＞（Ⅰ）＞（Ⅳ）。若测试介质黏度在该范围内，则控制应力边界下或控制剪速边界下不同运动黏度流体的瞬态平衡时间相差不大，均略滞后于转子自平衡时间（10 ms或50 ms），而且在该黏度范围内控制应力边界下流体的非稳态平衡时间更短。若υ＜20 mm2·s-1，采用控制剪速边界的平衡时间更短；若υ＞20000 mm2·s-1，则两类边界下的平衡时间相近。可见，表观黏度平衡时间除了取决于启动本身非稳态过程外，边界条件形式将大大影响整个非稳态阶段的平衡时间，即转子反馈调节达到设定应力或设定剪速的自平衡时间越长，启动初始的平衡时间越长。

3　结　论

（1）旋转流变仪在测试标准黏度液黏度时，初始阶段黏度测试值远高于其真实值。类推至与剪切历史密切相关的非牛顿流体，该段非稳态剪切所采集的数据将不能准确描述其流变性。

（2）旋转Couette流动的现有理论研究在边界条件上与流变仪测量间隙的实际边界存在差距。本研究将同轴圆筒流变仪测量间隙内的流动简化为由静止边界和运动边界组成的平板Couette流动，以牛顿流体为例求解了加载任意应力边界或剪速边界下的流场及表观黏度解析解，适用于边界函数不超过1个不可导点的任意情况，并求解了控制应力边界及控制剪速边界的6种边界条件下表观黏度解析解。

（3）本研究将两种间隙尺寸和运动黏度2～200000 mm2·s-1代入6种加载边界的解析解进行数值计算。计算结果表明：（Ⅲ）、（Ⅵ）平衡过程均体现为恒定值边界向线性增加边界的过渡，并在转子自平衡时间t0处存在“流场变化趋势”转变；测量间隙越大，表观黏度达到真实值的平衡时间越大；不同黏度的牛顿流体瞬态平衡时间不同，黏度越大剪切传递作用越强，越接近线性边界的平衡过程，黏度越小则越接近恒值边界的平衡过程。运动黏度υ＜20 mm2·s-1时，控制剪速边界下的瞬态平衡更快；运动黏度υ处于20～20000 mm2·s-1时，控制应力边界下的瞬态平衡更快，平衡时间略滞后于转子自平衡时间（10 ms）；运动黏度υ＞20000 mm2·s-1时，两类边界条件下的平衡时间相差不大。转子自平衡时间t0反映了流变仪机械响应的速度，是除启动流场非稳态外又一影响非稳态过程的重要因素。

（4）旋转流变仪测试系统复杂，可结合转子端部效应、测量夹具转动惯量等影响边界条件的机械因素对初始非稳态过程做进一步探讨。

符号说明

d，x——两无限大平板间距、与运动板距离，m

f（t） ——运动边界函数

M，M0——与时间有关的扭矩、设定扭矩值，N·m

n，n0——与时间有关的转速、设定转速值，r·min-1

t，t0——瞬态时间、转子自平衡时间，s

u（x，t） ——位置x时间t时的速度，m·s-1

βn——特征值，m

γ. ——剪速，s-1

ζ ——积分参量

μ，μf——牛顿流体黏度、瞬态表观黏度，Pa·s

σ ——应力，Pa

υ ——运动黏度，m2·s-1

ϕ ——相对黏度系数

References

［1］ ERDOĞAN M E. On the flows produced by sudden application of a constant pressure gradient or by impulsive motion of a boundary ［J］. International Journal of Non-Linear Mechanics， 2003， 38（5）：781-797. DOI： 10.1016/S0020-7462（01）00133-0.

［2］ TING T W. Certain non-steady flows of second-order fluids ［J］. Archive for Rational Mechanics and Analysis， 1963， 14（1）： 1-26. DOI：10.1007/BF00250690.

［3］ TAN W C， PAN W X， XU M Y. A note on unsteady flows of a viscoelastic fluid with the fractional Maxwell model between two parallel plates ［J］. International Journal of Non-Linear Mechanics，2003， 38（5）： 645-650. DOI： 10.1016/S0020- 7462（01）00121-4.

［4］ 潘文潇， 谭文长. 广义 Maxwell 黏弹性流体在两平板间的非定常流动［J］. 力学与实践， 2003， 25（1）： 19-22. DOI： 10.3969/j.issn. 1000-0879.2003.01.006. PAN W X， TAN W C. An unsteady flow of a viscoelastic fluid with the fractional Maxwell model between two parallel plates ［J］. Mechanics in Engineering， 2003， 25（1）： 19-22. DOI： 10.3969/j.issn. 1000-0879.2003.01.006.

［5］ PAPANASTASIOU T C， GEORGIOU G C， ALEXANDROU A N. Viscous Fluid Flow ［M］. Washington， D.C.： CRC Press， 1999： 209.

［6］ BOSE D， BASU U. Incompressible viscoelastic flow of a generalised Oldroyed-B fluid through porous medium between two infinite parallel plates in a rotating system ［J］. International Journal of Computer Applications， 2013， 79（1）： 13-20. DOI： http：//dx.doi.org/10. 5120/13704-1452.

［7］ 郭霄怡， 徐明瑜. 广义 Oldroyd-B 流体的非定常 Couette 流的精确解［J］. 山东大学学报（理学版）， 2009， 44（10）： 60-63. GUO X Y， XU M Y. An exact solution of unsteady Couette flow of generalized Oldroyd-B fluid ［J］. Journal of Shandong University（Natural Science）， 2009， 44（10）： 60-63.

［8］ HAYAT T， SAJID M， AYUB M. A note on series solution for generalized Couette flow ［J］. Communications in Nonlinear Science and Numerical Simulation， 2007， 12（8）： 1481-1487. DOI：10.1016/j.cnsns.2006.02.009.

［9］ ATHAR M， FETECAU C， KAMRAN M， et al. Exact solutions for unsteady axial Couette flow of a fractional Maxwell fluid due to an accelerated shear ［J］. Nonlinear Analysis： Modelling and Control，2011， 16（2）： 135-151.

［10］ BERNARDIN D， NOUAR C. Transient Couette flows of Oldroyd's fluids under imposed torques ［J］. Journal of Non-Newtonian Fluid Mechanics， 1998， 77（3）： 201-231. DOI： 10.1016/S0377-0257（97）00130-4.

［11］ PARTER S V， RAJAGOPAL K R. Remarks on the flow between two parallel rotating plates ［R］. Madison： Mathematics Research Center，Wisconsin Univ.， 1984.

［12］ RAJAGOPAL K R. Flow of viscoelastic fluids between rotating disks［J］. Theoretical and Computational Fluid Dynamics， 1992， 3（4）：185-206. DOI： 10.1007/BF00417912.

［13］ LAI C Y， RAJAGOPAL K R， SZERI A Z. Asymmetric flow between parallel rotating disks ［J］. Journal of Fluid Mechanics， 1984， 146：203-225. DOI： http：//dx.doi.org/10.1017/S0022112084001828.

［14］ DANIEL K S. Unsteady Couette flow with transpiration in a rotating system ［J］. Global Journal of Science Frontier Research， 2013， 13（5）：14-26.

［15］ SETH G S， JANA R N， MAITI M K. Unsteady hydromagnetic Couette flow in a rotating system ［J］. International Journal of Engineering Science， 1982， 20（9）： 989-999. DOI： 10.1016/0020-7225（82）90034-9.

［16］ SHEIKHOLESLAMI M， ABELMAN S， GANJI D D. Numerical simulation of MHD nanofluid flow and heat transfer considering viscous dissipation ［J］. International Journal of Heat and Mass Transfer， 2014， 79： 212-222. DOI： 10.1016/j.ij heatmasstransfer. 2014.08.004.

［17］ DANISH M， KUMAR S， KUMAR S. Exact analytical solutions for the Poiseuille and Couette-Poiseuille flow of third grade fluid between parallel plates［J］. Communications in Nonlinear Science and Numerical Simulation， 2012， 17（3）： 1089-1097. DOI： 10.1016/j.cnsns. 2011.07.037.

［18］ VARSAKELIS C， PAPALEXANDRIS M. Linear stability analysis of unidirectional Couette flows of inhomogeneous fluid-like bodies ［J］. Proceedings of the Royal Society of London， Series A Mathematical and Physical Sciences， 2014.

［19］ RAVEY J C， DOGNON M， LUCIUS M. Transient rheology in a new type of Couette apparatus ［J］. Rheologica Acta， 1980， 19（1）： 51-59. DOI： 10.1007/BF01523854.

［20］ RAVEY J C， IKEMOTO S， STOLTZ J F. Transient rheology in a new type of couette apparatus. Application to blood ［J］. Rheologica Acta，1989， 28（5）： 423-434. DOI： 10.1007/BF01336810.

［21］ BARAVIAN C， QUEMADA D. Correction of instrumental inertia effects in controlled stress rheometry［J］. The European Physical Journal Applied Physics， 1998， 2（2）： 189-195. DOI：http：//dx.doi.org/10. 1051/epjap：1998183.

［22］ GLEISSLE W. Two simple time-shear rate relations combining viscosity and first normal stress coefficient in the linear and non-linear flow range ［J］. Rheology， 1980， 2： 457-462. DOI：10.1007/978-1-4684-3743-0_85.

［23］ HUA C C. Investigations on several empirical rules for entangled polymers based on a self-consistent full-chain reptation theory ［J］. J. Chem. Phys.， 2000， 112（18）： 8176-8186. DOI： http：//dx.doi.org/ 10.1063/1.481418.

［24］ BORG T， PAAKKONEN E J. Linear viscoelastic models（Part Ⅱ）：Recovery of the molecular weight distribution using viscosity data ［J］. Journal of Non-Newtonian Fluid Mechanics， 2009， 156（1）： 129-138. DOI： 10.1016/j.jnnfm.2008.07.010.

Analytical and numerical studies on apparent viscosity in coaxial cylinder rotational rheometer during initial unsteady stage

XU Ruiyu， LIU Gang， CHEN Lei， TENG Houxing， LU Xingguo， XU Jikai
（College of Pipeline and Civil Engineering， China University of Petroleum （East China）， Qingdao 266580， Shandong， China）

During the initial testing stage with controlled stress or controlled shear rate， apparent viscosity is much higher than its true value because of factors such as transient flow process. Most existing researches about Couette flow in the measuring gap of coaxial cylinder rotational rheometer focus on constant boundary or time-dependent boundary in special form， which may has a gap with the actual changing boundary condition within rheometer. Thus， the arbitrary moving boundary condition was taken as f（t）， and the transient flow was simplified in coaxial cylinder for Couette flow into two infinite parallel plates. The exact solutions of apparent viscosity and velocity under controlled stress boundary and controlled shear rate boundary were derived through eigenfunction method and Laplace transform. Meanwhile， the numerical calculations of apparent viscosity under six boundary conditions were made according to two kinds of gap size and different viscosity （2—200000 mm2·s-1）. It showed that when the viscosity of newton fluid was below 20 mm2·s-1， the equilibrium of flow and apparent viscosity under controlled shear rate boundary cost less time. When the viscosity was among 20—20000 mm2·s-1， the equilibrium under controlled stress boundary cost less time. However， the equilibrium time under two kinds of boundary was nearly the same when the viscosity was over 20000 mm2·s-1.

date： 2015-06-09.

Prof. LIU Gang， liugang@upc.edu.cn

supported by the Innovation Youth Foundation Project in China University of Petroleum （East China） （14CX02107A）.

viscosity；hydrodynamics；numerical analysis；coaxial cylinder rotational rheometer；Couette；moving boundary condition；eigenfunction method

O 357.1； TE 81

A

0438—1157（2016）05—1784—07

2015-06-09收到初稿，2015-10-05收到修改稿。

联系人：刘刚。第一作者：徐睿妤（1990—），女，硕士研究生。

中国石油大学（华东）自主创新青年基金项目（14CX02107A）。