基于非负矩阵分解的多模态过程故障监测方法

朱红林，王　帆，侍洪波，谭帅

（华东理工大学化工过程先进控制和优化技术教育部重点实验室，上海 200237）



基于非负矩阵分解的多模态过程故障监测方法

朱红林，王帆，侍洪波，谭帅

（华东理工大学化工过程先进控制和优化技术教育部重点实验室，上海 200237）

针对传统的多元统计故障监测方法往往需要假设测量数据服从单一高斯分布的不足，提出了一种基于非负矩阵分解（NMF）的多模态故障监测方法。首先使用标准的NMF算法对训练集数据进行聚类，将多模态数据划分到各个模态中；然后使用稀疏性正交非负矩阵分解（SONMF）算法对各模态分别建模，同时构造监控统计量进行故障监测。将提出的基于非负矩阵分解的多模态故障监测方法应用于数值例子和TE过程的仿真结果表明，该方法能够及时有效地检测出多模态过程中的故障。

故障监测；多模态过程；非负矩阵分解

DOI：10.11949/j.issn.0438-1157.20151392

针对多模态过程监控问题，最直接的方法是采用多模型法，即对完全划分开的每一个模态的数据，使用研究单模态时的方法，分别建立监控模型，进行故障监控。这种方法有两个关键问题需要解决。第一个问题是如何将杂乱的多模态历史数据正确划分到各个模态中。目前常采用成熟的聚类算法如模糊c均值聚类、k均值聚类、多时段划分聚类等解决这一问题［5-7］。另一个问题是如何确定最终的监控结果。目前，主要有两种思路：一种是寻找到一个最符合当前生产状态的模型进行监控。另一种是将所有的局部模型都用于过程监控，并制定某种规则对局部模型的监控结果进行整合。若按照第1种思路，则需要建立一个合适的模型选择评价指标。Ng等［8］使用一个能够反映当前样本的2T和SPE的距离的指标来选择合适的PCA子模型。Feital等［9］通过优化一个极大似然函数来确定过程运行的模态。如果按照第2种思路，常需要利用当前样本相对于各局部模型的后验概率，通过贝叶斯推理，将各局部模型的监测结果进行整合。Yu等［10-11］和Xie等［12］分别利用高斯混合模型（Gaussian mixture model，GMM）和模糊c均值聚类计算各模型的后验概率，进行局部模型的整合。此外，刘帮莉等［13］通过带宽可变的非参数核密度函数进行局部密度估计，并利用局部密度因子的思想构造监测指标，能对多模态过程实现很好的监测效果。

非负矩阵分解（NMF）算法是一种新的降维方法。传统的多元统计过程监控方法需要假设测试数据服从一定的条件，如PCA需要测量数据服从于高斯分布。ICA能对非高斯数据进行有效处理，却对高斯数据的处理效果较差。而NMF算法对测量数据的性质除了非负性要求外没有其他要求，因此NMF的应用范围更加广泛，能够有效处理高斯及非高斯分布的数据。NMF算法是从“对整体的感知由对组成整体的部分感知构成”的观点出发而构建的数据处理方法。由于在机理上具有隐变量的正向纯加性的特点，NMF方法在实现数据压缩（或称为维数约简）时，能够基于数据的局部特征来描述数据的信息，因而表现出了比传统的方法如PCA等更好的数据解释能力。最近几年，NMF算法得到了越来越多的关注，并且在数据挖掘、模式识别、聚类［14-16］等方面得到了许多成功的应用。

然而，在化工过程的故障监测领域，NMF方法的应用相对较少。Li等［17］使用传统的NMF算法进行非高斯过程的故障监测，通过仿真实验不仅验证了NMF方法用于化工过程监测的有效性，而且相比于PCA方法拥有更广泛的应用能力。随后，Li等［18］对PNMF（投影非负矩阵分解）进行了改进，提出了对原始数据没有非负性约束的GNMP（广义非负矩阵投影）算法，大大扩展了NMF算法的应用范围。但是Li等虽在文章中提到了稀疏性对NMF算法的重要性，但却没有提出施加稀疏性的相关方法。Yi等［19］使用NMFSC（带稀疏限制的非负矩阵分解）进行故障检测，通过TE过程的仿真证明了该算法具有较好的故障检测能力。然而目前NMF算法在故障监测领域主要用于单模态的故障监测，多模态领域的应用还几乎没有涉及。

本文提出了基于非负矩阵分解的多模态故障检测方法。首先采用标准的NMF算法对多模态过程数据进行聚类，将多模态数据划分到相应的模态中。然后使用改进的NMF算法（SONMF，稀疏性正交非负矩阵分解）对每一个模态分别建模，进行故障监测。在使用SONMF方法对各模态进行故障监测的过程中，通过在非负矩阵分解的目标函数中施加稀疏性约束，以期得到数据集的更加稀疏的表示；通过在非负矩阵分解的目标函数中对基矩阵W施加正交性约束，以期在降维过程中大大削减变量中的冗余信息，得到更少的投影方向。最后通过对数值例子和TE过程的仿真实验，以证明NMF算法用于多模态故障监测的可行性以及改进后的NMF算法在各模态中故障监测性能。

1　非负矩阵分解

Lee等［20］首次系统性地提出了NMF算法及其相应的理论，其他扩展的NMF算法都是在此算法上进行相应的改进。为了与其他改进的算法进行区分，称Lee等提出的NMF算法为标准的NMF算法。

标准的NMF算法求解可以归结为一个优化的问题，所以需要定义相应的目标函数来度量分解的程度以及寻找一套合适的迭代规则。Lee等［21］为此定义了两种目标函数并给出了W和H的迭代规则，本文选用的目标函数如下。

目标函数为矩阵X与WH之间的Frobenius范数

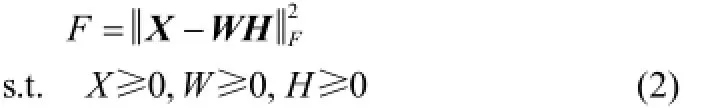
迭代规则如下

该目标函数单调非增，且目标函数不再变化的充分必要条件是W和H为稳定点。

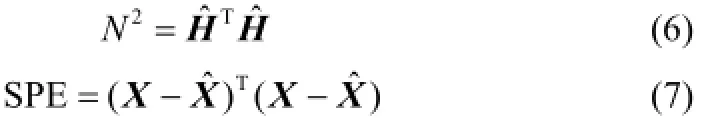
2　稀疏性正交非负矩阵分解

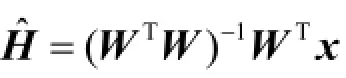
这个目标函数F中，不仅包含了对基矩阵W的正交约束，还包含了对于系数矩阵H的稀疏性约束。该目标函数的乘法更新公式如式（9）、式（10）所示。

通过式（9）、式（10）的乘法更新公式，可以得到过程监控模型如式（5）所示，相应的监测指标如式（6）、式（7）所示。

3　基于非负矩阵分解的多模态过程故障监测方法

基于上述介绍的标准的NMF算法和SONMF算法，这里提出一种新的多模态过程故障监测方法。

3.1初始化

NMF算法的结果往往与W和H的初始化有着很大关系，好的初始化值将有利于NMF快速收敛并且能获得更好的局部最优解。目前对于NMF算法的初始化问题主要有以下几种解决方案：（1）正随机数初始化方法；（2）利用奇异值分解（SVD）将原始数据分解，并将分解结果中的负元素置为零。

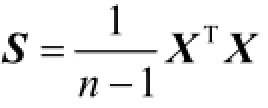
3.2NMF算法用于模态识别

标准的NMF算法分解前后的矩阵中的元素都是非负的，原始数据矩阵X中的任何一列向量都可以看成是基矩阵W中的所有列向量（基向量iw）的加权和，而权重系数为系数矩阵H中对应的列向量（系数向量jh）中的元素。因此，NMF算法的实质是将原始数据投影到由基向量iw所张成的子空间W上，而每一个样本在基矩阵W张成的子空间上均有唯一一种线性的表示形式，它们的坐标为系数矩阵H中相应的列向量。

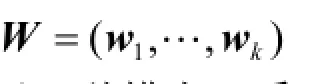
3.3多模态故障监测流程

多模态故障监测主要包括离线建模和在线监测两个阶段。离线建模和在线监测的示意图如图1、图2所示，其具体流程如下。

离线建模：

（1）对于多模态训练集数据，使用SVD算法对标准的NMF算法进行初始化，并利用乘法更新式（3）和式（4）计算出基矩阵mW和系数矩阵mH。

（2）根据系数矩阵mH的值，对多模态训练集数据进行聚类，将多模态训练集数据划分到各个的模态中。

（3）对于各模态数据，分别使用SVD算法对SONMF算法进行初始化，并利用乘法更新公式（9）和式（10）计算出各自的W和H。

图1　离线建模示意图Fig.1　Schematic diagram of offline modeling

（4）利用式（6）和式（7）分别计算多模态训练集数据在各模态下的监测指标2N和SPE的值，并使用KDE算法计算各模态监测指标的控制限。

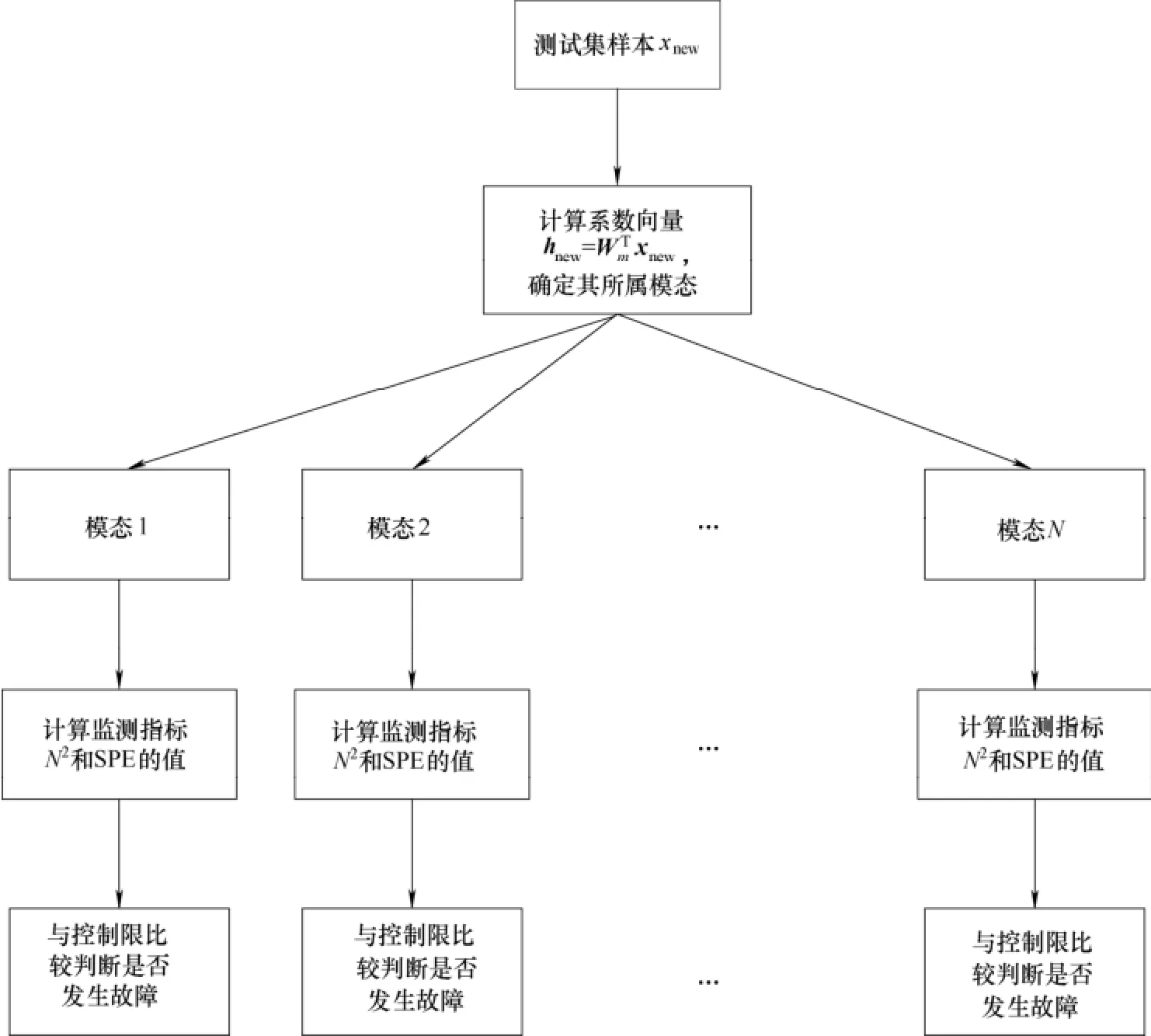
图2　在线监测示意图Fig.2　Schematic diagram of online process monitoring

在线监测：

（1）对于新的测试样本newx，计算它在多模态聚类模型下的系数向量Tnewnewmx= hW，根据它在多模态聚类模型构成的基向量mW上投影的大小，判断其所属模态。

（2）利用式（6）和式（7）计算该测试样本newx在所属模态下的监测指标2N和SPE的值。（3）比较该测试样本的监测指标2N和SPE的值与所属模态下的控制限的关系，若大于控制限则发生故障，小于控制限则无故障发生。

4　仿真验证

本节通过数值例子与TE过程的仿真研究来证明本文提出方法的有效性。使用SONMF算法对各模态数据分别建立模型并构造统计量进行故障监测。标准的NMF算法同样可以用于各模态过程监测［17］，将标准的NMF与SONMF算法检测结果进行比较，可以证明SONMF通过对目标函数施加正交性和稀疏性约束，其故障监测能力远优于标准的NMF算法。

4.1数值仿真

在两种模态下分别采集400个正常样本，从而产生800个正常样本作为训练集。设置两个故障如下所示。故障1：过程运行在mode 1下，从第401个样本点起，给变量5x施加一个幅值为4阶跃故障。故障2：过程运行在mode 2下，从第401个样本点起，给变量1x施加一个斜率为0.02的漂移故障。测试集由800个样本组成，其中前400个样本为正常样本，后400个样本为故障样本。

首先，使用标准的NMF算法对训练集数据进行聚类，将训练集数据划分到mode 1和mode 2中。因为训练集由两个模态数据组成，所以降维阶数k设为2。算法的迭代次数设为1000。此时基矩阵W的两列（1w和2w）分别代表两个聚类中心。系数矩阵H作为判定指标，判定数据所属的模态。对训练集的聚类结果如图3所示。其中红色点表示该数据样本属于mode 1，绿色点表示该数据样本属于mode 2。由图3可以看出标准的NMF算法能很好地完成聚类任务。

图3　模态1和模态2数据样本的聚类结果Fig.3　Clustering results of data samples from mode 1 and mode 2

对聚类得到的两个模态数据分别使用SONMF算法以及标准的NMF算法分别建模，进行故障监测，并进行比较。根据前面初始化时所提出的k的选取方法，经过计算k值取为4。算法的迭代次数均设为1000。在SONMF算法中，对于λ、α值的选取，从乘法更新公式［式（12）和式（13）］可以看出，当λ、α越小，其正交性约束能力与稀疏性性约束能力越小；当λ、α均为0时，SONMF算法就退化为标准的NMF算法；而当λ、α取值过大时，将不利于乘法更新公式的进行。因此，经过多次尝试，λ的值取为1，α的值取为10。对于故障1和故障2的监测结果如表1所示。

表1　R数值仿真的故障监测率Table 1　Fault detection rates of the numerical example/%

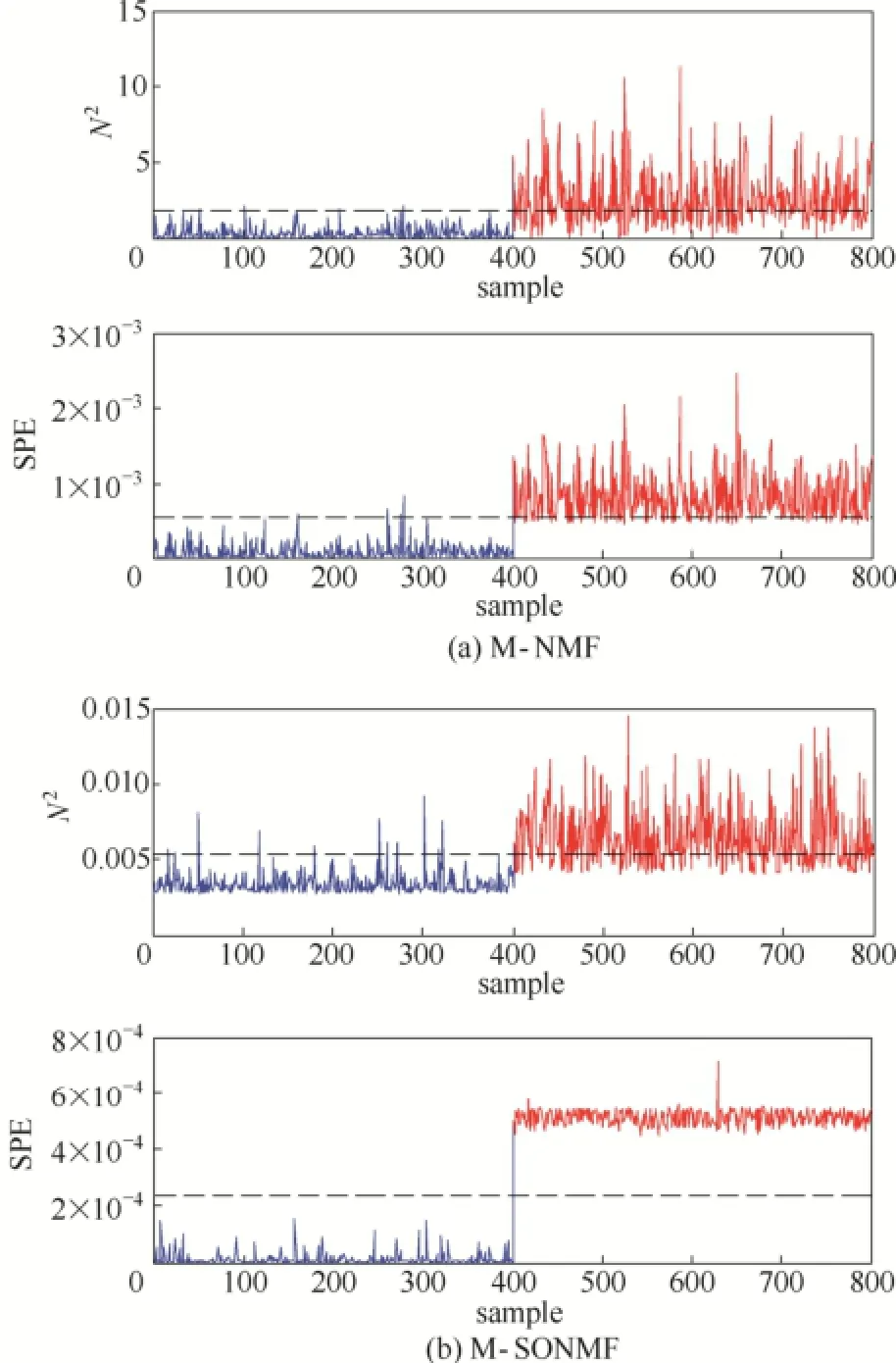
图4　故障1的故障检测结果Fig.4　Monitoring results of M-NMF and M-SONMF for fault 1

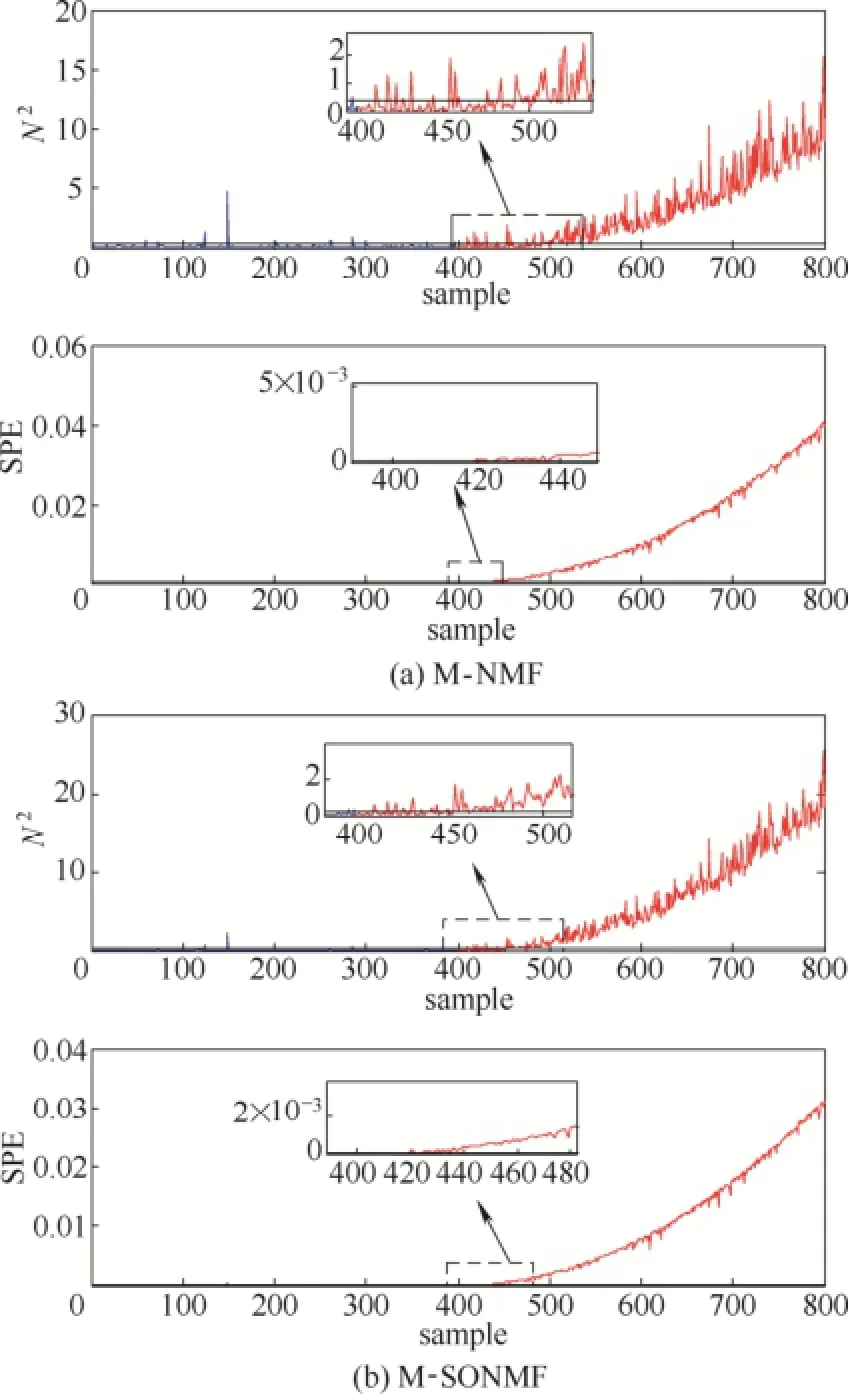
图5　故障2的故障检测结果Fig.5　Monitoring results of M-NMF and M-SONMF for fault 2

4.2TE过程仿真

TE过程是一个复杂的多变量化工生产过程，可人为设定21种故障，目前已被广泛用于评价过程监测方法的有效性。TE过程主要包括5个操作单元：反应器、冷凝器、压缩机、分离器、汽提塔［23］。它包含8种成分：4种反应物、2种产品、1种副产品、1种惰性气体。TE过程中共有41个测量变量和12个控制变量。其中测量变量由22个连续过程测量变量和19个非连续过程测量变量组成。在仿真过程中，控制变量5、9、12始终保持不变，因此选用剩余的9个控制变量以及22个连续过程变量进行仿真分析。根据产物G与H比例的不同，TE过程可分为多种运行模态，Downs等［23］给出了6种工况的最优稳定运行条件。本文对TE过程的mode 1和mode 3两个模态下的20类故障进行监测。训练集由模态1下的1000个正常数据样本和模态3下的1000个正常数据样本组成。测试集由1000个数据样本组成，其中前200个数据样本是正常样本，后800个数据样本是故障样本。

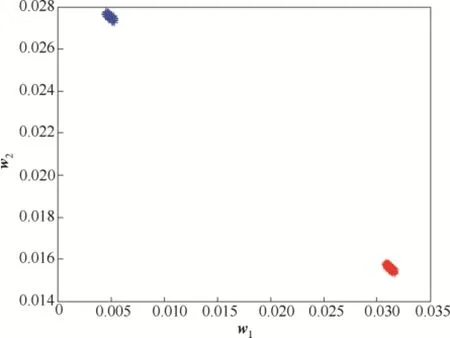
图6　模态1和模态3数据样本的聚类结果Fig.6　Clustering results of data samples from mode 1 and mode 3

首先，使用标准的NMF算法对训练集数据进行聚类，将训练集数据划分到mode 1和mode 3中。因为训练集中数据可以分为2类，所以降维阶数k设为2。算法的迭代次数设为1000。此时基矩阵W的两列（1w和2w）分别代表两个聚类中心。系数矩阵H作为判定指标，判定数据所属的模态。对训练集的聚类结果如图6所示。其中红色点表示该数据样本属于mode 1，绿色点表示该数据样本属于mode 3。

系统中选用的SIM300 GPRS无线数传模块内嵌TCP/IP协议簇，模块与单片机通过串口进行通信，选择TCP协议作为GPRS的传输协议,模块自身便会自动完成Internet网络的接入，实现数据的传输。调用AT指令对SIM300模块进行初始化设置，单片机通过串口发送AT命令，控制SIM300模块上网登录，建立TCP连接，进行数据的远程无线传输。GPRS驱动程序主要函数如下：

对聚类得到的各模态数据使用SONMF算法以及标准的NMF算法分别建模，进行故障监测，并进行比较。根据前面初始化时k选取方法，经过计算k取为18。算法的迭代次数均设为1000。在SONMF算法中，对于参数λ、α值的选取，根据在上节数值仿真中的讨论，λ的值取为1，α的值取为10。上述两种算法的故障监测结果如表2、表 3所示。

在模态1中，对于故障3、5、9、15、16，由于测试数据在均值、方差和高阶矩上都没有明显变化，所以使用多元统计方法得到的故障监测率都很低［24］，M-NMF算法与M-SONMF算法对故障的监测结果都很差。在其余的故障情况下，M-NMF和M-SONMF的方法的误报率始终在5%以内。对于故障1、2、6、7、8，因为这些故障发生时的故障程度很明显，所以两种算法的故障检测率都很高。从表2可以看出，对于故障4、10、11、12、13、14、17、18、19和20，M-SONMF算法的故障监测结果都优于M-NMF算法。其中故障4、10、11、14、17、18、19的N2指标以及故障10、12、14、18、19、10的SPE指标，M-SONMF算法相比于M-NMF算法有超过10%的提高。

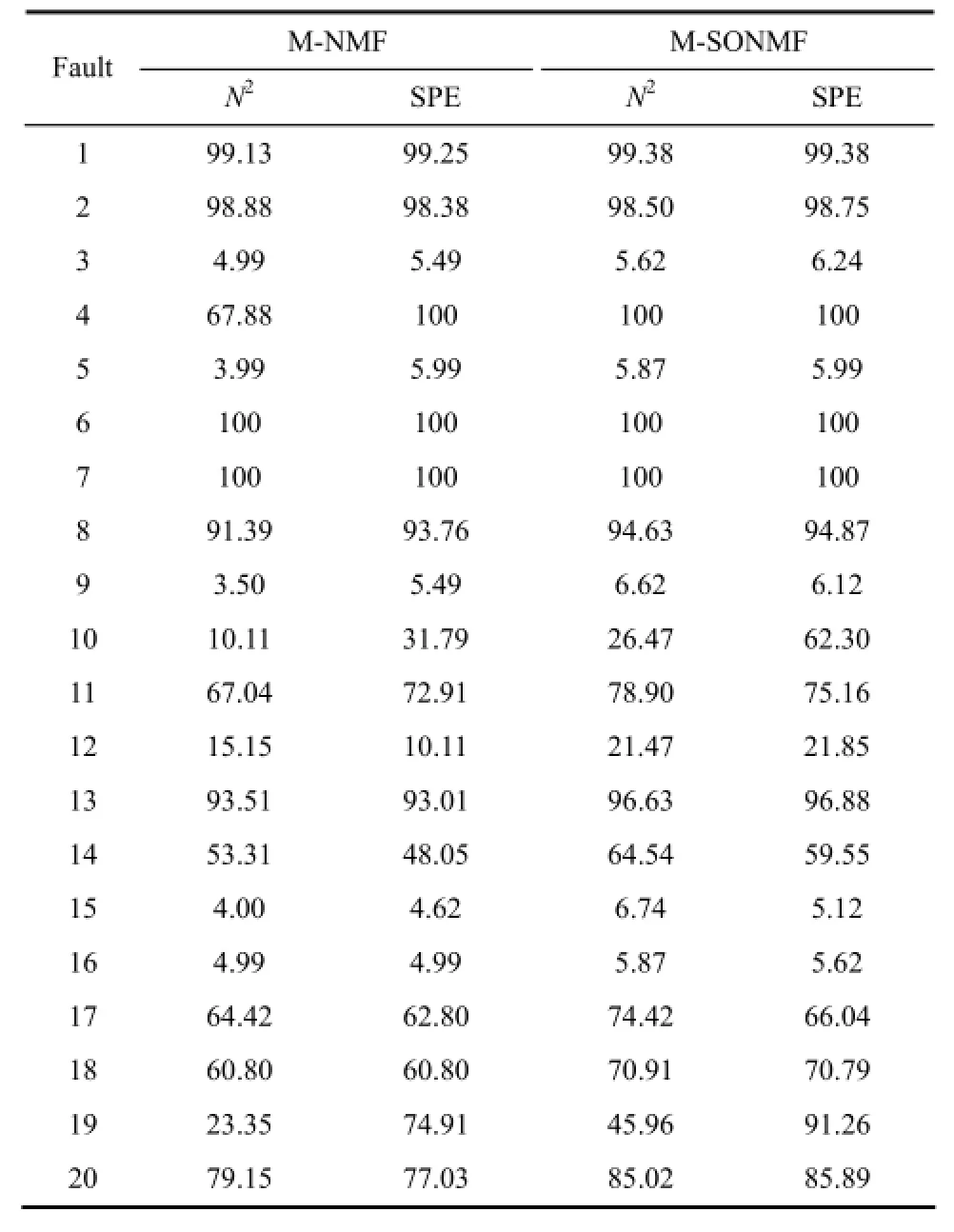
表2　RTE过程模态1的20个故障的监测率Table 2　Fault detection rates of 20 faults in TE mode 1/%

表3　RTE过程模态3的20个故障的监测率Table 3　Fault detection rates of 20 faults in TE mode 3/%

从表3可以看出，M-SONMF算法与M-NMF算法用于模态3的故障监测结果和用于模态1的故障监测结果相似。在模态3下，M-SONMF算法的监测结果往往明显优于M-NMF算法的监测结果，如故障20的SPE指标提高了23.97%。

从整体上看，M-SONMF算法的故障监测效果明显好于M-NMF算法。这是因为M-SONMF算法一方面对矩阵元素施加了稀疏性约束，增强了对于数据的压缩性与可解释性，使降维后得到更少的投影方向；另一方面，在分解过程中对基矩阵W进行正交化处理，除去变量间的冗余信息，使得更少的投影方向可以代表更多的信息。通过上述两点的改进，使得M-ONMF算法的监控效果较M-NMF算法有了大幅提升。

5　结　论

本文针对复杂工业生产过程中存在多个模态，数据分布未知的问题，提出了一种基于NMF的多模态故障监测方法。首先利用标准的NMF算法对多模态过程数据进行聚类，然后对每个模态建立SONMF模型来描述每个模态的统计特性。在进行故障监测时，通过判断待检测样本所属的模态，并且计算出该样本在所属模态中的监测指标值，进行故障监测。本文中使用SONMF算法对工业过程的各模态分别建模，通过对标准的NMF算法进行了稀疏性的限制，得到对数据集更稀疏的表示；通过在标准的NMF算法的目标函数中对基矩阵W施加正交约束，使得在对原始数据降维的过程中大大削减了变量中的冗余信息，得到更少的投影方向，因此在对故障进行监测时能得到更好的监测结果。通过对数值例子和TE过程的仿真研究证明了NMF算法用于多模态故障监测的可行性以及SONMF算法在各模态中拥有比标准的NMF算法更好的故障监测性能。由于模态间的过渡十分短暂，工业过程大部分时间处于某一稳定模态，故本文中并没有考虑到模态间的过渡。这一问题将在以后进行进一步研究。

References

［1］ZHOU D H， HU Y Y. Fault diagnosis techniques for dynamic system［J］. Acta Automation Sinica， 2009， 35 （6）： 748-758.

［2］WOLD S， ESBENSEN K， GELADI P. Principal component analysis［J］. Chemometrics & Intelligent Laboratory Systems， 1987， 2 （1/2/3）：37-52.

［3］NOMIKOS P， MACGREGOR J F. Multi-way partial least squares in monitoring batch processes ［J］. Chemometrics & Intelligent Laboratory Systems， 1995， 30 （1）： 97-108.

［4］GE Z Q， SONG Z H， GAO F R. Review of recent research on data-based process monitoring ［J］. Industrial & Engineering Chemical Research， 2013， 52 （10）： 3543-3562.

［5］赵春晖， 王福利， 姚远， 等. 基于时段的间歇过程统计建模、在线监测及质量预报 ［J］. 自动化学报， 2010， 36 （3）： 366-374. ZHAO C H， WANG F L， YAO Y， et al. Phase-based statistical modeling， online monitoring and quality prediction for batch process［J］. Acta Automatica Sinica， 2010， 36 （3）： 366-374.

［6］GE Z Q， SONG Z H. Multimode process monitoring based on Bayesian method ［J］. Journal of Chemometrics， 2009， 23 （12）： 636-650.

［7］SEBZALI Y M， WANG X Z. Knowledge discovery from process operational data using PCA and fuzzy clustering ［J］. Engineering Applications of Artificial Intelligence， 2001， 14 （5）： 607-616.

［8］NG Y S， SRINIVASAN R. An adjoined multi-model approach for monitoring batch and transient operations ［J］. Computers & Chemical Engineering， 2009， 33 （4）： 887-902.

［9］FEITAL T， KRUGER U， DUTRA J， et al. Modeling and performance monitoring of multivariate multimodal process ［J］. AIChE Journal，2013， 59 （5）： 1557-1569.

［10］YU J， QIN S J. Multimode process monitoring with Bayesian inference-based finite Gaussian mixture models ［J］. AIChE Journal，2008， 54 （7）： 1811-1829.

［11］YU J. Online quality prediction of nonlinear and non-Gaussian chemical processes with shifting dynamics using finite mixture model based Gaussian process regression approach ［J］. Chemical Engineering Science， 2012， 82 （1）： 22-30.

［12］XIE X， SHI H B. Multimode process monitoring based on fuzzy C-means in locality preserving projection subspace ［J］. Chinese Journal of Chemical Engineering， 2012， 20 （6）： 1174-1179.

［13］刘帮莉， 马玉鑫， 侍洪波. 基于局部密度估计的多模态过程故障检测 ［J］. 化工学报， 2014， 65 （8）： 3071-3081. LIU B L， MA Y X， SHI H B. Multimode process monitoring based on local density estimation ［J］. CIESC Journal， 2014， 65 （8）： 3071-3081.

［14］SHANG F， JIAO L C， WANG F. Graph dual regularization non-negative matrix factorization for co-clustering ［J］. Pattern Recognition， 2012， 45 （6）： 2237-2250.

［15］LONG X Z， LU H T， PENG Y， et al. Graph regularized discriminative non-negative matrix factorization for face recognition ［J］. Multimedia Tools & Applications， 2014， 72 （3）： 2679-2699.

［16］ZENG K， YU J， LI C H， et al. Image clustering by hyper-graph regularized non-negative matrix factorization ［J］. Neurocomputing，2014， 138 （11）： 209-217.

［17］LI X B， YANG Y P， ZHANG W D. Fault detection method for non-Gaussian processes based on non-negative matrix factorization［J］. Asia-Pacific Journal of Chemical Engineering， 2013， 8 （8）：362-370.

［18］LI X B， YaANG Y P， ZHANG W D. Statistical process monitoring via generalized non-negative matrix projection ［J］. Chemometrics & Intelligent Laboratory Systems， 2013， 121 （7）： 15-25.

［19］PENG Y， CHEN X， Ye Q X， et al. Fault detection and classification in chemical processes using NMFSC and structural SVMs ［J］. The Canadian Journal of Chemical Engineering， 2014， 92 （6）： 1016-1023.

［20］LEE D D， SEUNG H S. Learning the parts of objects by non-negative matrix factorization ［J］. Nature， 1999， 401 （6755）： 788-791.

［21］LEE D D. Algorithms for non-negative matrix factorization//Adv. Neural Inform. Process. Syst. ［C］. MIT Press， Cambridge， MA， USA， 2001， 32 （6）：556-562.

［22］GE Z Q， SONG Z H. Multimode process monitoring based on Bayesian method ［J］. Journal of Chemometrics， 2009， 23 （12）：636-650.

［23］DOWNS J J， VOGEL E F. A plant-wide industrial process control problem ［J］. Computers & Chemical Engineering， 1993， 17 （3）：245-255.

［24］YU J B. Local and global principal component analysis for process monitoring ［J］. Journal of Process Control， 2012， 22 （7）： 1358-1373.

Fault detection method based on non-negative matrix factorization for multimode processes

ZHU Honglin， WANG Fan， SHI Hongbo， TAN Shuai
（Key Laboratory of Advanced Control and Optimization for Chemical Processes of Ministry of Education，East China University of Science and Technology， Shanghai 200237， China）

The traditional multivariate statistical fault detection methods are designed for single operating conditions and may produce erroneous conclusions if they are used for the multi-mode process monitoring. A novel multi-mode process monitoring approach based on non-negative matrix factorization （NMF） is proposed in this paper. First， the training set of data is clustered by the standard NMF algorithm and the multi-mode data are divided into each mode. Then， the sparseness orthogonal NMF （SONMF） algorithm is used to model every mode and the monitoring statistics are constructed to perform fault detection. The proposed method is applied to a numerical example and the TE process. The simulation results show that this method can effectively detect multi-mode process failure.

fault detection； multi-mode process； non-negative matrix factorization

引　言

过程监控方法能够及时发现过程运行中出现的故障并通知操作人员，极大提高了工业过程运行的安全性和稳定性［1］。近年来，传统的多元统计过程监控（multivariate statistical process monitoring，MSPM）方法如主成分分析（PCA）［2］、偏最小二乘（PLS）［3］等在工业过程中得到了成功的应用。但是，传统的多元统计过程监控方法需要假设测量数据均服从于高斯分布，且都来自于单一稳定的模态［4］。然而在实际的工业生产中，过程往往并不是运行在单一的稳定模态下，产品特性、生产负荷、原料组分等的变化，都能引起模态的变化。此时若仍用传统的方法进行故障监控，则会削弱过程在不同模态下的统计特性，从而造成过程性能分析不准确以及过程故障的大量漏报。

date： 2015-09-06.

Prof. SHI Hongbo， hbshi@ecust.edu.cn

supported by the National Natural Science Foundation of China （61374140） and the Youth Foundation of the National Natural Science Foundation of China （61403072）.

TP 277

A

0438—1157（2016）05—1973—09

2015-09-06收到初稿，2016-02-24收到修改稿。

联系人：侍洪波。第一作者：朱红林（1991—），男，硕士研究生。

国家自然科学基金项目（61374140）；国家自然科学基金青年基金项目（61403072）。