非均匀热通量对热电器件性能的影响

明廷臻，潘　滔，王乾坤，周军莉，杨威，龚廷睿

（1武汉理工大学土木工程与建筑学院，湖北 武汉 430070；2华中科技大学能源与动力工程学院，湖北 武汉 430074；3上汽通用汽车有限公司武汉分公司产品工程部，湖北 武汉 430200）



非均匀热通量对热电器件性能的影响

明廷臻1，潘滔2，3，王乾坤1，周军莉1，杨威2，龚廷睿2

（1武汉理工大学土木工程与建筑学院，湖北 武汉 430070；2华中科技大学能源与动力工程学院，湖北 武汉 430074；3上汽通用汽车有限公司武汉分公司产品工程部，湖北 武汉 430200）

提高冷热两端温度是提高热电器件发电效率的有效途径之一。但当施加于热端表面的热通量不均匀时，热端表面温度不均匀，系统性能受到影响。基于此，建立了热电器件的热电转换耦合数学模型，分析热电材料物性参数，非均匀热通量等参数对热电器件的功率输出特性的影响。数值模拟结果表明：材料物性参数随温度的变化对系统输出功率的影响不可忽略，热通量4 W·cm-2时物性参数对系统最高温度的影响接近4%；非均匀热通量对热电器件输出特性影响也十分显著，热通量均匀度越小，热端表面温度分布不均匀性越大，极值温度越高，高温区越小，断路电压越低。

太阳能热电发电器；热通量；热传导；均匀度；数值模拟

引　言

热电发电技术是一种新能源发电技术，它利用温差条件下晶格中载流子和声子运动所伴随的能量和电荷转移特性实现热能和电能的转换。利用该技术可将太阳能、核辐射产生的热能、工业废热等转化为电能［1-3］。热电发电器件具有体积小、质量轻、无噪声、无污染、无运动部件、运行环境要求低等优点，可实现低品位热能的利用，故热电发电技术已引起广泛的关注［4-6］。

目前，对热电技术的研究主要集中在以下几个方面：（1）研究热电材料以期提高材料的热电优值［7-10］，提高材料的热电优值可显著提高热电模块的效率；（2）热电模块的功率输出特性理论、实验及运行特性优化研究［11-13］；（3）热电模块的结构优化及采用层叠式电偶臂结构以提高系统的效率［14］。此外，相关热电器件的工程应用也有较多报道［15-16］。

热电发电和热电制冷技术与太阳能相结合已成为太阳能利用的主流技术之一。通过聚光集热技术提高太阳能的能流密度并将其施加于接收器表面，可显著提高系统的性能［17-18］。本文作者在武汉市地铁项目的太阳能利用研究中，提出一种基于电润湿法的微流控光学太阳能聚光技术［19］与热电发电器相结合的新型太阳能集成系统，将微流控光学太阳能聚光器接收到的太阳能通过高倍聚光并施加于热电模块的热端表面，提高冷热两端温差，从而提高发电效率。微流控光学太阳能聚光器能够将太阳能热通量提高几百倍。但研究发现，高聚光比导致热电器件的非均匀受热，特别是高热通量下接近或超过其材料承受极限时，反而也会引起效率下降，发生热应力破坏等问题。因此，本文着重分析在非均匀的高热通量下，热电器件的温度分布特征和电压输出性能。此外，非均匀的高热通量下，材料的物性参数受温度的影响非常显著，本文也将同时考虑高热通量下变物性参数对系统性能的影响。

1　物理数学模型

1.1物理模型

本文采用的热电发电器件包含18对电偶臂，如图1所示。模型基本尺寸如下：L×W×H= 7a×7a×1.8a（其中a=0.004 m），单个热电模块为立方体，边长为a，铜板厚度d1=0.2a，聚热层厚d2=0.2a，相邻热电模块之间的间距是d3=0.2a。假设各层材料接触良好，忽略接触热阻和接触电阻的影响。在图1所示结构中，聚热层和铜板均分为上下两部分。特别指出，图1的几何结构是基本对称的，但铜板是连接电偶臂从而实现电流串联的材料，由于它的存在，使得整个内部结构不是中心对称的。聚热层有绝缘效果，而铜板电阻小，电能在内阻上有消耗，故聚热层和铜板的配合可以将回路保证在热电模块内，同时减小内阻消耗；同时，聚热层的比热容比铜板大，铜板比聚热层导热性能好，导热过程中可以保证热端和冷端的温差。

图1　热电器件物理模型Fig.1　Physical model of thermoelectric device

1.2数学模型

利用微流控光学太阳能聚光器聚集的高倍热流施加于热电器件的热端表面，之后在热电器件内部不同材料之间以及热端和冷端之间产生温度梯度，从而使闭合回路产生电流。这是一个典型的热能和电能的耦合能量转换过程，该过程满足能量守恒方程和电流连续性方程［20］

式中，λ为热导率；T为温度；ρ为电阻率；J为电流密度；α为Seebeck系数。相应的电流密度和热通量分别为

式中，σ为电导率；μ为迁移率。

1.3边界条件

计算热电器件的温度分布时，其边界条件比较复杂。太阳辐射进入微流控光学太阳能聚光器［19］后，调整聚光倍数，所聚集成的高强度辐射直射到热电器件的热端表面上。若忽略过程中的各种损失，可将其视为直接施加于热端表面的热流量，因此可将接收到热流的热端表面视为给定热流边界，而未接受到热流的热端表面区域则可视为绝热边界。热电模块的下表面为低温端，并设为环境温度20℃；热电器件的侧面以及电偶臂表面均视为绝热边界。在进行热电耦合分析时，需设置电势参考点，故以图1中坐标系为参考，选择（7a，0.4a，6a）为电势零点

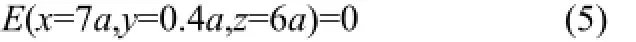
由于壁面上电流无法穿过壁面，可得

热电器件下表面为冷端，设为恒温20℃

假设热电模块热端表面的总面积是S，热流量Q施加在热端表面上面积为A的区域内。定义热流均匀度r为热端表面接受热流的面积A与热电模块热端表面总面积S的比：r=A/S。则热端表面接受热流的面积A上的热通量q为

在r值不同的工况下，热通量q也相应发生变化。当r=1时，表明热通量均匀分布于热端表面；r＜1时，则热电器件的热端表面有部分没有接收到太阳辐射，此时热电器件接收到非均匀的热通量，r越小，这种非均匀性越大。据此，可以计算得到这些不同工况下热电器件的温度分布特征和电压输出特性。

计算采用有限元计算方法，离散耦合上述方程，利用热电耦合进行分析，热电耦合单元为solid226，网格皆为结构性网格（六面体）。为验证计算的网格无关性，在考虑材料物性参数的影响下，数学模型为式（1）～式（4），边界条件为式（5）～式（8），网格数量分别为12995、58972和103960个，得到3种网格数量下模块最高温度，计算得这3种网格数量对计算结果的影响在2%以内，故可认为是网格无关的。本文选取的计算网格均为58972。

工作过程中，电偶臂的温度从热端到冷端沿程逐渐减小。当电偶臂的温度梯度过大，其材料的物性参数将会随着温度发生变化，故计算时应考虑温度变化对物性参数的影响。本文选用的热电材料为Bi2Te3，常物性参数取值见表1（该参数温度为180℃），将影响热电器件性能的主要物性参数［21］随温度的变化特征进行多项式拟合。

表1　R180℃时热电材料Bi2Te3的物性参数Table 1　Thermophysics parameters of Bi2Te3at 180℃

2　模拟结果及分析

2.1r=1下变物性参数对系统性能的影响

太阳能能流密度范围最高可达1000 W·m-2，基于电润湿法的微流控光学太阳能聚光技术［19］的聚光倍数最高可达1000倍，因此施加于接收表面的热通量最大可达100 W·m-2。假设太阳辐射分别为100、200、300、400 W·m-2，太阳能聚光系统的聚光倍数为100，则设施加于热端表面A上的热通量q分别为1、2、3、4 W·cm-2，分别对常物性（表1）和变物性条件下热电器件的性能进行非稳态计算。相应的温度结果如图2所示。

图2　物性参数对热电器件热端表面温度的影响Fig.2　Influence of thermophysics paramters on hot end surface temperature of thermoelectric device

由图2可见，不同热通量条件下，热电器件热端温度的变化趋势基本一致，可分为3段：温度快速上升期、平稳上升期和稳定期。快速上升期时间在0～100 s，此阶段开始前，整个系统与冷端温度保持一致，接收到高热通量后，热端表面温度迅速升高，并沿着热电臂向冷端方向传递能量。热电臂沿程吸热、储热、传热，造成热端表面温度上升显著，当通过热端表面的热扰动深入到物体内部并且已经抵达冷端之后，进入了100～200 s时热端表面的温度平稳上升期。此时热端温度不再发生显著上升，而且冷热端两端温差不再显著增加。当t＞200 s之后，除了热能向电能转换的能量之外，剩余部分将从低温段导出；传递到热端的热量与从低温面导出的热量随时间基本不变，此时热电模块空间各点的温度随时间基本不变，系统慢慢从准稳态进入稳态导热阶段，因此热端表面温度曲线表现为一条水平直线，随时间的变化很小。

此外，增大热通量时，温度快速上升期和平稳上升期的斜率也增大，热电器件热端表面在一个更高的温度水平上达到稳定。根据傅里叶导热定律，在热通量q较大，而热导率λ与厚度dx都相同的条件下，dt会更大，即温差会更大，高温端温度会更高，故稳定期高温端温度会更高。同时，由图2可见，当热通量较小时（q=1 W·cm-2），常物性和变物性曲线几乎重合；随着热通量增加下，常物性和变物性曲线的差异越来越大，这说明，当热通量较高时，材料物性参数随温度的影响变得较为显著。为了进一步对比变物性的影响及分析产生差异的原因，分别将常物性和变物性两条曲线的差值的相对值和绝对值表示出来，结果如图3所示。

图3（a）中定义相同条件下，常物性和变物性下热电器件热端表面的温度差异为

图3（b）中常物性和变物性下热电器件热端表面温度的相对差异定义为

图3（a）的曲线趋势与图2大致相同，也可分为快速上升期、平稳上升期和稳定期，形成原因也和图2一致。图3（a）温差曲线显示，热通量越小，常物性和变物性温差越小，因为热电模块的温度沿热传导方向变化，热通量越小，温度梯度越小，温度变化对物性参数的影响越小，故温差越小，反之，热通量越大，热电模块的温度梯度越大，温度变化对物性参数的影响越大，温差越大。

图3（b）显示的曲线规律与图3（a）差异较大。图3（b）曲线可以分为3个部分，快速下降区、平稳上升区和稳定区。与图3（a）不同，图3（b）曲线下降表示常物性和变物性下曲线的温度差异减小，曲线上升则意味着常物性与变物性下温度的差异增大。如表1所示，热电材料的常物性参数值设置为180℃，而模型的初始计算温度为20℃，此时与常物性设置值相差较大，故相对差异较大。热电模块热端受热温度上升过程中，热电材料物性参数的平均值与常物性设置值逐渐接近，因而在图中表现为曲线下降，最终达到谷值；随着时间推移，热电模块温度逐渐上升，热电器件的整体温度都逐渐增大，变物性参数的平均值与常物性参数的差异都会先减小再增大，从而每段曲线都会有谷值。谷值之后，平稳上升期与图2、图3（a）中的平稳期对应，此时模块温度上升变缓；最后的稳定期与图2、图3（a）规律也基本类似，从热端传导到模块的热量刚好由冷端散失，达到能量平衡。与图2中快速上升期的斜率相对应，热通量越高，温度上升越快，达到谷点的时间越短。图3（b）中q为4、3 W·cm-2两端曲线满足上述规律，但又有例外，这两段曲线在t=200 s附近有交点，而后q=4 W·cm-2的温度相对差异反而略小，对比图2看到q为4、3 W·cm-2的高温端温度分别在200和155℃，综合考虑热电器件温升值，其温度变化分别为200℃-20℃=180℃和155℃-20℃=135℃。对比半导体材料的N，P极Seebeck系数与热导率的多项式拟合函数，可以发现其物性参数并非是单调函数，有类似抛物线的极值，而这两种情况的高温端在物性参数极值的两端，对q=4 W·cm-2，有部分材料工作在最佳温度范围内，所以对比q=3 W·cm-2，变物性参数的温度影响反而略小。

图3　常物性和变物性参数下温度相对差异Fig.3　Absolute and relative temperature difference under constant and variable thermophysics parameters

2.2非均匀热流对系统输出特性的影响

为研究非均匀热通量对热电器件输出特性的影响，需同时改变热流均匀度r和热通量q，以保证总热流量Q一定。假设Q总量不变，为7.84 W，则当热流均匀度r从1减小到1/49时，q也从1 W·cm-2变化到49 W·cm-2。另一方面，为增加结果研究的普遍性，热流量Q的值从7.84 W增加到47.04 W。相应的施加案例及计算得到的热端表面最高温度见表2，相应的温度分布和电压分布如图4、图5所示。

由图4可见，非均匀热通量对热电器件温度分布均匀性的影响非常显著。当热通量分布的均匀度较小时，热端表面存在一个高温区；r越小，该高温区的面积越小，相应的极值温度越高，这不利于提高热电器件的发电性能。随着热通量均匀度r的增加，热电器件热端表面的温度分布变得越均匀。需要指出，图4中有些温度云图并不对称，原因如下：（1）模块内部结构并非是完全对称，沿x和z轴方向的内部结构不同，如r=1/49时温度云图，x、z方向云图各自轴对称，但系统不是中心对称；（2）施加非均匀热通量边界条件时，热负荷实际施加在网格上，而为保证热流均匀度r及总热流量Q，所施加的网格数在热端表面并未呈现中心对称的布局，从而导致了温度云图的不均匀。图5为非均匀热通量对热电器件断路电压的影响，图中显示均匀度对电压云图的影响较小，下文将进一步分析这种影响。

表2　R非均匀热通量对热端表面最高温度的影响Table 2　Influence of non-uniform heat flux on maximum temperature of hot end surface

图4　非均匀热通量对热电器件温度分布的影响Fig.4　Influence of non-uniform heat flux on temperature distribution of thermoelectric device （Q=7.84 W）

图5　非均匀热通量对热电器件断路电压的影响Fig.5　Influence of non-uniform heat flux on open-circuit electric potential distribution of thermoelectric device （Q=7.84 W）

图6为不同的热流量Q下，热通量均匀度r对热电器件最高温度的影响。由图可见，不同热流量下的曲线变化规律基本一致，随着热通量均匀度r的增加，热电模块的热端表面最高温度显著减小，这一点与图4结果基本一致，当热通量均匀度为r=1/49，Q=47.04 W时，热电器件的热端表面最高温度达850℃以上；相应地，保持均匀度不变而减少热流量Q至7.84 W，热电器件的热端表面最高温度降至100℃左右；而保持热流量Q不变而增大热通量均匀度r为1，则其最高温度略高于250℃。另一方面，热流量Q从7.84 W增加至47.04 W，r=1/49条件下引起的热电器件热端表面最高温度的增加值比r=1时的增加值高得多。由此可见，热通量均匀度对热电器件最高温度的影响十分显著。

图7为非均匀热通量对热电器件输出电压的影响规律。由图可见，相同热流量Q条件下，减小热通量的均匀度r，系统的输出电压呈现减小的趋势，但总体来说，输出电压的减小不太明显。当热通量均匀度r较小时，输出电压才显著降低。这种现象在热流量Q较高时愈发明显。这是因为热通量均匀度r越小，热端表面的高温区域越小，高温区域的极值温度越高，能量损失越大。当热流量Q为7.84 W，均匀度为1/49时，高温面最高温度刚超过100℃，而在热流量为47.04 W，均匀度为1/49时，高温面最高温度已经达850℃，此时热辐射的影响将非常大，故这种影响在图中可以直观看出；同时，当均匀度相同，热流量不同时，对比相邻两条曲线发现，增加相同的热流量，输出电压会增加，但增加的程度逐渐降低，也是因为随着热流量逐渐增加，高温面温度逐渐升高，热辐射影响逐渐增加。

图6　热通量均匀度r对热电模块上表面最高温度的影响Fig.6　Influence of heat flux uniformity on hot end surface maximum temperature of thermoelectric device

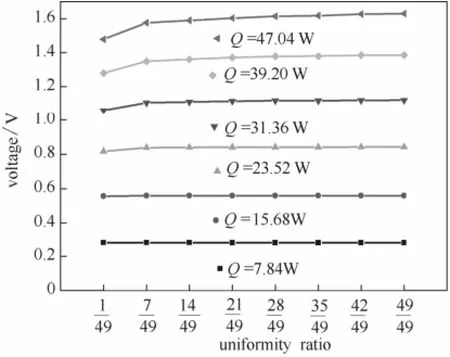
图7　非均匀热通量对输出电压的影响Fig.7　Influence of non-uniform heat flux on output electric potential

为了进一步阐述热通量均匀度r对输出电压的影响，定义输出电压相对差异如式（11）所示

图8所示为热通量均匀度r对热电器件输出电压相对差异的影响规律。可见，热通量均匀度r对输出电压相对差异的影响非常显著。热通量均匀度r越小，对输出电压的影响越大。特别地，当热流量为47.04 W，热通量均匀度r为1/49时，对输出电压的相对差异接近10%。对比图6中的温度曲线可知，此时热电器件热端表面的最高温度达855℃，在热流量从47.04 W到7.84 W，热通量均匀度r为1/49的变化过程中，热电器件的最高温度逐渐降低，故热辐射换热量逐渐减小，其对热电器件电压输出特性的影响也逐渐减小。

图8　热通量均匀度r对热电器件输出电压相对差异的影响Fig.8　Influence of heat flux uniformity on relative difference of output electric potential of thermoelectric device

3　结　论

建立了热电器件热电耦合数学模型，分析了非均匀高热通量和热电材料物性参数对热电器件的温度分布及电压输出特性的影响规律。研究结果表明：

（1）热电材料物性参数对热电器件结果的影响不可忽略，当热通量q为4 W·cm-2时，热电材料物性参数对系统最高温度的影响接近4%。

（2）热通量均匀度r对热电器件性能的影响十分显著。①在一定的总热流量条件下，热通量越小，热电器件热端表面温度分布均匀性越小，最高温度越高，如当总热流量Q=47.04 W，热通量均匀度为r=1/49时，热电器件的热端表面最高温度可达850℃以上；②较小的热通量均匀度也对系统输出电压造成显著的影响，如当热流量为47.04 W，热通量均匀度r为1/49时，对输出电压的相对差异接近10%。

References

［1］ BELL L E. Cooling， heating， generating power， and recovering waste heat with thermoelectric systems ［J］. Science， 2008， 321（5895）：1457-1461.

［2］ GUO R Q， HUANG B L. Thermal transport in nanoporous Si：anisotropy and junction effects ［J］. International Journal of Heat and Mass Transfer， 2014， 77：131-139.

［3］ SHEN L M， CHEN H X， XIAO F， et al. The step-change cooling performance of miniature thermoelectric module for pulse laser ［J］. Energy Conversion and Management， 2014， 80：39-45.

［4］ POUDEL B， HAO Q， MA Y， et al. High-thermoelectric performance of nanostructured bismuth antimony telluride bulk alloys ［J］. Science，2008， 320（5876）： 634-638.

［5］ UR S C， KIM I H， NASH P. Thermoelectric properties of Zn4Sb3directly synthesized by hot pressing ［J］. Materials Letters， 2004，58（15）： 2132-2136.

［6］ RAO A M. Properties of nanostructured one-dimentional and composite thermoelectric materials ［J］. MRS Bulletin， 2006， 31（3）：218-223.

［7］ VENKATASUBRAMANIAN R， SIIVOLA E， COLPITTS T， et al. Thin-film thermoelectric devices with high room-temperature figures of merit ［J］. Nature， 2001， 413（6856）： 597-602.

［8］ ZHAO X B， JI X H， ZHANG Y H， et al. Bismuth telluride nanotubes and the effects on the thermoelectric properties of nanotubecontaining nanocomposites ［J］. Applied Physics Letters， 2005， 86（6）：062111-3.

［9］ SHARMA S， PANDEY S K. A first principle study of electronic band structures and effective mass tensors of thermoelectric materials：PbTe， Mg2Si， FeGa3and CoSb3［J］. Computational Materials Science，2014， 85： 340-346.

［10］ SHARP J W， JONES E C， WILLIAMS R K， et al. Thermoelectric properties of CoSb3and related alloys ［J］. Journal of Applied Physics，1995， 78（2）： 1013-1018.

［11］ 申利梅， 陈焕新， 梅佩佩， 等. 热电制冷模块热连接与电连接的性能优化分析［J］. 化工学报， 2012， 63（5）： 1367-1372. DOI：10.3969/j.issn.0438-1157.2012.05.006 SHEN L M， CHEN H X， MEI P P， et al. Optimization analysis on thermal connection and electrical connection of thermoelectric refrigeration modules ［J］. CIESC Journal， 2012， 63（5）： 1367-1372. DOI： 10.3969/j.issn.0438-1157.2012.05.006

［12］ MING T Z， WU Y J， PENG C， et al. Thermal analysis on a segmented thermoelectric generator ［J］. Energy， 2015， 80（1）： 388-399.

［13］ 张博， 王亚雄. 热电制冷液体冷却散热器的实验研究［J］. 化工学报， 2014， 65（9）： 3441-3446. DOI： 10.3969/j.issn.0438-1157. 2014.09.018 ZHANG B， WANG Y X. An experimental investigation on a novelliquid thermoelectric cooling device ［J］. CIESC Journal， 2014， 65（9）：3441-3446. DOI： 10.3969/j.issn.0438-1157.2014.09.018

［14］ SANDOZ-ROSADO E J. Investigation and development of advanced models of thermoelectric generators for power generation applications［D］. New York： Rochester Institute of Technology， 2009.

［15］ HSU C T， HUANG G Y， CHU H S， et al. Experiments and simulations on low-temperature waste heat harvesting system by thermoelectric power generators ［J］. Applied Energy， 2011， 88（4）：1291-1297.

［16］ HEREMANS J P， THRUSH C M， MORELLI D T. Thermopower enhancement in lead telluride nanostructures ［J］. Physical Review B，2004， 70（11）： 115334.

［17］ ECK M， UHLIG R， MERTINS M， et al. Thermal load of direct steam-generating absorber tubes with large diameter in horizontal linear Fresnel collectors ［J］. Heat Transfer Engineering， 2007， 28（1）：42-48.

［18］ RHYEE J S， LEE K H， LEE S M， et al. Peierls distortion as a route to high thermoelectric performance in In4Se3-xcrystals ［J］. Nature， 2009，459（7249）： 965-968..

［19］ CHENG J， PARK S， CHEN C L. Optofluidic solar concentrators using electrowetting tracking： concept， design， and characterization［J］. Solar Energy， 2013， 89（1）： 152-161.

［20］ WU Y， MING T， LI X， et al. Numerical simulations on the temperature gradient and thermal stress of a thermoelectric power generator ［J］. Energy Conversion and Management， 2014， 88（12）：915-927.

［21］ ROWE D M. Thermoelectrics Handbook： Macro to Nano ［M］. New York： CRC Press Taylor & Francis Group， 2005： 21-1-16.

Influence of non-uniform heat flux on performance of thermoelectric device

MING Tingzhen1， PAN Tao2，3， WANG Qiankun1， ZHOU Junli1， YANG Wei2， GONG Tingrui2
（1School of Civil Engineering and Architecture， Wuhan University of Technology， Wuhan 430070， Hubei， China；2School of Energy and Power Engineering， Huazhong University of Science and Technology， Wuhan 430074， Hubei， China；3Product Engineering Department， Wuhan Branch of SAIC-GM Ltd.， Wuhan 430200， Hubei， China）

An effective approach to increase the output power efficiency of thermoelectric devices is to increase the temperature difference between the hot and cold ends of thermoelectric devices. However， when the heat flux being imposed upon the hot end is non-uniform， the temperature distribution on the hot surface is uneven， which will influence the overall performance of the device. Based on this， a conjugate thermal to electric energy conversion mathematical model of thermoelectric devices was established to analyze the influences of thermoelectric material properties， non-uniform heat flux on the output power performance of thermoelectric device. Numerical simulation results indicated that the influence of temperature dependent material properties on the system output power cannot be neglected and the influence on the system maximum temperature difference will approach 4% when heat flux is about 4 W·cm-2. The non-uniform heat flux has significant influence on the output power of thermoelectric device. The less the uniformity of heat flux upon the hot end of thermoelectric device， the more uneven of temperature distribution on the hot end， the maximum temperature， the high temperature region and the open-circuit voltage will be.

date： 2015-09-06.

Prof. MING Tingzhen， tzming@whut.edu.cn

supported by the Wuhan Metro Group Co.， Ltd. Foundation （WHRT-KY-201016）， the Scientific Research Foundation of Wuhan University of Technology （40120237）， the Fundamental Research Funds for the Central Universities （2016IVA029） and the National Natural Science Foundation of China （51106060）.

solar thermoelectric power generator； heat flux； heat conduction； uniformity； numerical simulation

10.11949/j.issn.0438-1157.20151409

TM 913

A

0438—1157（2016）05—1798—08

2015-09-06收到初稿，2016-01-11收到修改稿。

联系人及第一作者：明廷臻（1976—），男，教授。

武汉地铁集团有限公司资助项目（WHRT-KY-201016）；武汉理工大学科研启动基金项目（40120237）；中央高校基本科研业务费专项资金资助（2016IVA029）；国家自然科学基金项目（51106060）。