湍动流化床内固体颗粒扩散系数

周弼辉，赵　明，梁俊宇，陆　勇，肖　睿

（1东南大学能源热转换及其过程测控教育部重点实验室，江苏 南京 210096；2云南电网有限责任公司电力科学研究院，云南 昆明 650217）



湍动流化床内固体颗粒扩散系数

周弼辉1，赵明2，梁俊宇2，陆勇1，肖睿1

（1东南大学能源热转换及其过程测控教育部重点实验室，江苏 南京 210096；2云南电网有限责任公司电力科学研究院，云南 昆明 650217）

将高速摄影及基于互相关原理的图像处理技术与颗粒扩散规律的研究进行结合，对湍动流化床中甲醇制烯烃催化剂SAPO-34颗粒的扩散系数进行了实验研究。实验表明，对于Geldart A类的SAPO-34颗粒，颗粒纵向扩散系数在10-2～10-1m2·s-1量级之间，横向扩散系数在10-3～10-2m2·s-1量级之间，两者均随流化风速的上升而增大。另外，在相同的流化风速下，粒径较小的颗粒具有更大的扩散系数。该结果对湍动床颗粒运动规律的研究有一定意义。

湍动；流态化；粒子图像测速；扩散系数；甲醇制烯烃

引　言

湍动流态化是介于鼓泡流态化和快速流态化之间的一种流型。相较于鼓泡流态化和快速流态化，湍动流态化具有气泡尺寸小、固含率高、气固两相接触更加剧烈、气固热量交换和质量交换更优、床内流动特性相对均匀等优点［1-2］。目前许多涉及化学反应的工业流化床都采用湍动流态化的形式，如费托合成（Fischer-Tropsch synthesis）反应、催化裂化（fluid catalytic cracking）的再生反应、无催化剂的流化床反应器、颗粒干燥等。

了解流化床反应器中固体颗粒的混合和扩散规律对于量化流化床内化学反应的各项参数有重要意义。鼓泡流化床和循环流化床中气固两相运动规律已有大量文献研究，然而由于湍动流态化的复杂性，对于湍动流化床内颗粒运动规律的研究并不多见。目前对于湍动流化床内颗粒混合与扩散运动的研究多采用实验方法，由于研究者采用的方法各不相同，实验条件复杂多样，取得的结果也有很大差别［3］。Avidan等［4］利用磁性示踪颗粒研究了湍动流态化过程中的固体颗粒混合行为，并利用一维扩散模型分析了固体颗粒的轴向扩散。Lee等［5］利用稳态热流技术研究了Geldart B类颗粒在湍动流化床中的气固两相扩散系数，发现湍动流态化过程中固体颗粒的轴向扩散系数随表观气速的上升而增大。Mostoufi等［6］利用放射性示踪颗粒研究了湍动流化床内固体颗粒的轴向和径向扩散系数，也同样发现颗粒的扩散行为随着表观气速的增加而显著加剧。由于方法所限，这些研究并未涉及颗粒的径向扩散行为。因此Du等［7］采用电容层析成像法研究了湍动流化床内颗粒轴向和径向扩散系数，发现湍动床内颗粒的径向扩散系数也随着表观气速的增大而增大。然而，通过示踪颗粒研究湍动床内颗粒混合行为的方法需要解决示踪颗粒的注入、检测、分离等问题，操作烦琐，过程复杂，实验结果的重复性不甚理想［1］。因此本文采用图像法研究湍动流化床内固体颗粒的扩散规律，意图通过采集并分析颗粒运动的图像以建立湍动床内颗粒纵向和横向扩散系数研究的新方法。

图像法是一种非接触式的多相流研究方法，相较于化学示踪颗粒法、电容层析成像法等方法而言，可以直观展现出流场内颗粒运动的物理形态，并且能够截取颗粒运动的瞬时信息，对于固体颗粒浓度较低、透明度较好的流场来说，可以取得较好的测量效果。朱建新等［8］利用图像法测量了二维流化床内颗粒的运动速度，通过互相关原理得到了颗粒的速度分布；严建华等［9］利用图像法分析了二维气固流化床内密相区颗粒混合过程；罗娅等［10］利用高速摄影及图像追踪算法研究了鼓泡床密相区颗粒横向混合特性。本文在对颗粒运动的图像进行分析时也应用了互相关原理，同时结合亚像素拟合、错误向量修正、图像偏置等方法，从图像中提取出颗粒运动的位移信息，并进一步得出颗粒的纵向及横向扩散系数。

本研究的对象为甲醇制烯烃（methanol to olefin，MTO）反应催化剂SAPO-34颗粒。甲醇制烯烃是我国烯烃生产的主要技术路线，其反应器之一为湍动床。研究催化剂颗粒SAPO-34在湍动床内的扩散规律对分析其在湍动床内的停留时间分布有一定意义［11］，进而可以通过对颗粒停留时间分布的分析实现催化剂积炭量的调控，从而提高烯烃的产率。然而，目前对于SAPO-34颗粒在湍动床内扩散规律的研究并不多见，因此希望通过高速摄影及基于互相关原理的图像处理技术对Geldart A类的SAPO-34颗粒在湍动床内的扩散系数进行实验研究，为工程应用提供参考。

1　实　验

实验装置为普通玻璃和有机玻璃及不锈钢联合搭建的二维冷态流化床实验台。流化床的上升段为普通玻璃和不锈钢搭建而成的腔体，高1.5 m、宽0.3 m，前后两块普通玻璃之间间隔4 mm，两侧用不锈钢包边。与有机玻璃相比，普通玻璃可以有效减小所用颗粒与壁面间的静电效应，对于图像法来说是更好的选择。流化床上部的扩大段和下部的风室用有机玻璃搭建。流化床布风板采用孔径20 μm、厚2 mm的金属烧结板。实验装置如图1所示。

采用的流化颗粒为平均粒径70、80和100 μm的甲醇制烯烃催化剂SAPO-34颗粒。实验流化风速从0.5 m·s-1逐渐增大至1.0 m·s-1。经过计算，所用颗粒在这一气速范围内在流化床中呈湍动状态。

实验采用的照明装置为150 W的LED灯。为使光线均匀柔和地照亮被摄区域，在流化床扩大段后一块玻璃板的背面粘了一张绘图用的硫酸纸。实验采用的高速相机为Photron公司生产的Fastcam高速相机，以每秒1000帧的速度采集图片，然后再通过图像处理算法对采集到的图片进行处理，提取颗粒的位移信息，进而计算颗粒的扩散系数。

图1　实验装置Fig.1　Experimental set-up

2　图像处理方法

2.1互相关原理

根据颗粒运动的位移信息，可以计算出单个颗粒的扩散系数［12］

式中，Δrn为颗粒在Δt时间内的位移。进而可求得床内颗粒平均扩散系数

刘道银等［13］应用式（1）、式（2）对流化床密相区颗粒扩散系数进行了CFD数值模拟，通过引入理想示踪粒子成功计算了床内平均颗粒扩散系数，为预测大型流化床内颗粒扩散速率提供了良好的方法。由此可见，颗粒在Δt时间内的位移是计算颗粒扩散系数的关键。在应用图像法计算颗粒位移的过程中主要应用互相关原理［14-16］，通过在图像中一定位置选取一定尺寸的方形区域作为“判读区”，进而对判读区进行信号处理以获取颗粒的位移。假设系统在t0以及t0+Δt这两个时刻分别获取了一张图片，在这两张图片中相同的位置选取两个同样尺寸大小的判读区f（m， n）以及g（m， n），（m， n）表示f与g分别在这两张图片中的相对位置。对f与g进行处理就可以获得此判读区对应位移s。判读区f、g与位移向量s之间数字信号传递函数关系如图2所示（图中大写字母分别是对应小写字母的傅里叶变换）。

图2　互相关分析传递函数图Fig.2　Transfer function diagram of cross correlation analysis

图中f（m， n）表示系统输入，g（m， n）表示系统输出，s（m， n）表示空间位移函数（对应于系统的脉冲响应），d（m， n）表示附加的噪声，此噪声是由于粒子离开判读区的边缘或者粒子通过三维运动进入光屏所造成的。另外，f（m， n）和g（m， n）的原始采样也必然包含噪声。图像分析主要任务是计算空间位移函数s（m， n），但噪声d（m， n）的出现使问题变得复杂。整个系统的工作关系式为

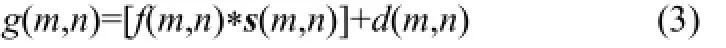
*表示f与s的卷积运算。假定噪声信号可以忽略，对式（3）两边分别进行傅里叶运算可得

大写字母分别代表各自小写字母的离散傅里叶变换。S（u， v）的近似结果可以通过式（1）获得，如果d（m， n）的作用可以忽略，逆向变换S（u， v）就可以恢复位移函数s（m， n）。

需要指出的是，互相关原理并不旨在计算出每一个具体颗粒的位移信息，而是将图像划分为若干网格，即“判读区”，再对每一个判读区进行信号处理，得到每一个判读区内的颗粒平均位移。本文虽然采用针对单个颗粒的扩散系数公式，但并不将其用在具体的每一个颗粒上，而是将其用在每一个判读区上，最终得到的结果是每一个判读区的颗粒扩散系数。简而言之，本文通过互相关计算建立起判读区与判读区内颗粒的联系，再通过式（1）、式（2）建立起判读区颗粒平均位移与判读区颗粒扩散系数之间的联系。互相关原理好比一座桥梁，将“某一区域内的颗粒”与单颗粒联系了起来。

为了得到准确的颗粒位移信息，在实际计算的过程中，还需要在互相关原理的基础上结合亚像素拟合、错误向量修正、图像偏置、迭代算法、变形窗口算法［17-19］等。

2.2亚像素拟合及错误向量修正

图像法得到的实验图像最小单位为1个像素，因此通过上述互相关算法得到的结果存在±1个像素的误差。根据Nyquist采样定律，对于大小为N=64个像素的判读区，通过互相关原理计算得到的位移大小不能超过N/2，进而可以得到此时的误差，大约为1/（64/2）=3.13%。这样大的误差在图像提取这一环节是不可接受的，必须使用曲线拟合方法将计算结果精度提高到±0.1个像素精度（即亚像素精度），进而使误差降低至0.3%左右。亚像素拟合主要有3种方法：中心拟合、抛物线拟合以及高斯拟合，其中三点高斯拟合得到最广泛的使用，其拟合公式为

另外，在实际情况下，由于无法做到采集图像中各个局部地区均能满足颗粒分布均匀的要求，所以互相关计算结果中经常出现少数明显有错误的矢量，因此速度修正方法往往是计算后必不可少的一个步骤，修正的基本思路是：根据流体连续性方程，一个计算点周围的速度与该计算点之间的差异不能太大，如图3所示。

图3　错误向量修正Fig.3　Schematic diagram of error vector correction

其中，U2D（i， j）表示通过互相关原理计算所得的结果，U（1）～U（8）分别表示周围8个计算结果。本文采用的错误向量修正公式为

其中，U2D，mean为U（1）～U（8） 8个计算结果的平均值，εthresh为判断阈值。式（6）表示，当|Udiff，n|大于阈值εthresh时，就认为计算结果为错误结果，予以剔除，并以中值滤波法计算结果代替U2D（i， j）。所谓的中值滤波算法即是将计算结果与周围邻近的U（1）～U（8） 8个计算结果按照数值大小进行排序，将排序后的中间值替换错误的计算结果。

2.3图像偏置及迭代算法

互相关原理的基本思想为在两幅图中相同位置分别选取同样大小尺寸的判读区进行互相关计算。互相关计算结果表明，判读区内的流体微团存在一个位移。因此就连续两帧图像而言，如果在后一帧图像的判读区取有一定偏置的图像，再进行互相关计算，所得结果会更加准确。Westerweel等［17］的研究结果表明图像偏置可以有效提高信噪比，改善计算精度。

如果在前一次计算的基础上，缩小判读区尺寸，再引入图像偏置算法，就可以形成迭代算法。由于综合了互相关计算以及图像偏置技术这二者特点，迭代算法结果比没有迭代的计算结果更为精确，但迭代计算过程比较费时间。

本文中相应的判读区尺寸（像素）迭代变化为：128→64→32→16→8→4。上一次使用的大判读区的计算结果，作为下一次小判读区计算的预报值，并使用这个预报值进行图像偏置的互相关计算。

2.4变形窗口算法

对于变化比较强烈的旋涡或者对流等速度变化梯度比较大的流场，由于同一个判读区内的颗粒运动方向和大小不一致，因此计算结果有一定误差。此时需要引入变形窗口算法来解决这个问题：该算法与迭代算法类似，通过第1次的粗略计算结果，使用人工图像合成技术，在第2幅已经由于流动变形后的图像中，再次合成一幅与第1幅图像接近的图像，进行互相关计算；并且将本次计算的结果来修正上一次的结果，不断循环计算，直到合成的图像与第1幅图像几乎一致为止。通过这种变形窗口计算方式，可以有效抵消由于速度场剧烈变化引起的计算误差，不断地循环修正逼近真实值。本文所用的图像处理手段如图4所示。

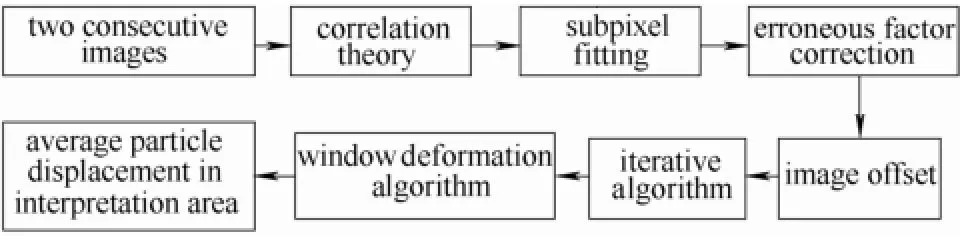
图4　图像处理流程Fig.4　Image processing flow chart

3　结果与讨论

3.1颗粒位移计算

实验时用高速相机记录下颗粒运动的图像，图5中的两幅图像即为平均粒径100 μm的SAPO-34颗粒在流化风速为1.0 m·s-1时，通过高速相机记录下的连续两帧运动图像。

图5　1.0 m·s-1流化风速下连续两帧颗粒运动图像Fig.5　Two continuous frames of particle motion under 1.0 m·s-1operating gas velocity

颗粒在两帧图像的拍摄间隙，即1 ms内的位移十分微小，肉眼几乎无法察觉其间的变化，因此图5中两幅图像看起来差别并不明显，但对这连续的两帧颗粒运动图像后利用前述的互相关原理进行计算，即可得出颗粒在两帧图像的间隔时间，即1 ms内的位移。换句话说，互相关方法的计算结果揭示了连续两帧颗粒运动图像之间的变化。通过示例图图5中的两幅图片计算得到的位移矢量图如图6所示。

必须指出的是，矢量图中的箭头标示的并不是每一个颗粒的位移，而是每一个判读区内颗粒的平均位移，这也是互相关算法的关键所在。利用互相关算法计算之后，再结合亚像素拟合、错误向量修正、图像偏置算法、迭代算法及变形窗口算法对结果进行处理。本文将这些方法进行了有机结合，通过判读区的有效划分而使得用判读区内的位移代表实际的位移情况成为可能。

在实际情况下，各个颗粒的运动方向不尽相同，为了分别计算颗粒的纵向扩散系数和横向扩散系数，需要对利用互相关算法计算得到的位移结果进行归并，即分别计算出每一个判读区内颗粒平均位移的纵向和横向分量，也就是判读区内颗粒的平均纵向分位移和平均横向分位移，进而通过式（1）、式（2）计算出颗粒在这一时间间隔内的平均纵向扩散系数和平均横向扩散系数。

图6　连续两帧图像计算所得位移矢量图Fig.6　Displacement vector diagram calculated according to two continuous frames of particle motion

湍动床内的颗粒运动具有很强的随机性，因此实验过程中的图像采集均在稳定状态下进行。对每个工况，本文均采用500张图片计算得到的平均值来代表每个工况下颗粒的平均横向扩散系数和纵向扩散系数。

3.2流化风速对颗粒扩散系数的影响

研究表明，鼓泡流化床内颗粒扩散系数随流化风速的上升而增大。Thiel等［20］、Avidan等［4］的研究均反映了这一变化趋势。Geldart［21］认为，随着流化风速的不断上升，气泡运动愈发剧烈，不断混合、聚并、破碎，使得整个床层内的颗粒运动也随之加剧，颗粒的纵向和横向扩散系数也都随之增大。

本文实验表明，这一趋势在流化床过渡到湍动流化床后仍在加剧。如图7、图8所示，湍动流态化过程中，流化风速对甲醇制烯烃催化剂SAPO-34颗粒的横向扩散系数和纵向扩散系数均有显著影响。随着流化风速的不断增大，颗粒的横向扩散系数和纵向扩散系数不断上升。Mostoufi等［6］、Du等［7］的实验结果也反映了相似的趋势。

本实验计算得到的湍动床颗粒平均纵向扩散系数普遍在10-2～10-1m2·s-1量级，颗粒平均横向扩散系数多在10-3～10-2m2·s-1量级。颗粒横向扩散速率较纵向扩散速率更慢是已经被人们认识到的事实，本文的计算结果也反映了这一现象。

图7　流化风速对颗粒平均纵向扩散系数Da的影响Fig.7　Influence of flow velocity on longitudinal diffusion coefficient Daof particles

图8　流化风速对颗粒平均横向扩散系数Dr的影响Fig.8　Influence of flow velocity on lateral diffusion coefficient Drof particles

3.3颗粒尺寸对颗粒扩散系数的影响

颗粒尺寸对颗粒在湍动床内的纵向和横向扩散系数的影响也在本文实验中得到了研究。本文分别对平均粒径为70、80、100 μm的颗粒进行了扩散系数的实验研究。如图9、图10所示，在相同的流化风速下，粒径较小的颗粒具有更大的扩散系数，粒径较大的颗粒纵向和横向扩散都弱于粒径较小的颗粒。本文实验中颗粒尺寸对颗粒扩散系数的影响并不十分显著。

图10　颗粒粒径对横向扩散系数Dr的影响Fig.10　Effect of particle size on lateral diffusion coefficient Dr

4　结　论

将图像法结合到湍动流态化固体颗粒扩散规律的研究中，提出了分析湍动床内固体颗粒扩散系数的新方法。利用高速相机记录下二维湍动床中固体颗粒的运动图片，并通过互相关原理以及亚像素拟合等技术得到颗粒在连续两帧图像之间的位移信息，进而根据式（1）、式（2）计算出颗粒的平均纵向扩散系数和横向扩散系数。

应用的流化颗粒为甲醇制烯烃催化剂SAPO-34颗粒。实验表明，该颗粒在流化风速从0.5 m·s-1增大至1.0 m·s-1的过程中，颗粒的纵向扩散系数和横向扩散系数均随流化风速的上升而增大。颗粒的平均纵向扩散系数在10-2～10-1m2·s-1量级，平均横向扩散系数在10-3～10-2m2·s-1量级。还通过实验研究了颗粒粒径对颗粒扩散系数的影响，对平均粒径为70、80和100 μm的SAPO-34颗粒分别进行了扩散规律的实验研究。实验表明，在相同的流化风速下，粒径较小的颗粒具有更大的扩散系数。

传统的图像法只能观察靠近壁面薄层的流动规律，对流化床内的物理过程进行非接触式的测量。本文采用的图像法亦属于传统的图像法范畴，所以实验也只能在透明玻璃制成的二维床中进行，并不能直接将这一实验手段应用于工业过程。在实际的工业过程中，传统图像法采用的非接触式拍摄手段显然并不可取，针对这一问题，目前已有研究者开发出介入式的光纤探头［22］，试图解决工业过程中的图像采集问题。本文的研究旨在探究如何应用颗粒运动的图像得到湍动床内颗粒的扩散系数，结合新的工业过程颗粒运动图像采集手段，即可依照本文所述得到颗粒的扩散系数，对工业过程做出一定指导。

References

［1］ 金涌， 祝京旭， 汪展文， 等. 流态化工程原理［M］. 北京：清华大学出版社， 2001. JIN Y， ZHU J X， WANG Z W， et al. Fluidization Engineering Principles ［M］. Beijing： Tsinghua University Press， 2001.

［2］ 郭慕孙， 李洪钟. 流态化手册［M］. 北京： 化学工业出版社， 2008. KUO M， LI H Z. Handbook of Fluidization ［M］. Beijing： Chemical Industry Press， 2008.

［3］ BI H T， ELLIS N， ABBA I A， et al. A state-of-the-art review of gas-solid turbulent fluidization ［J］. Chemical Engineering Science，2000， 55（21）： 4789-4825.

［4］ AVIDAN A， YERUSHALMI J. Solids mixing in an expanded top fluid bed ［J］. AIChE Journal， 1985， 31（5）： 835-841.

［5］ LEE G S， KIM S D. Axial mixing of solids in turbulent fluidized beds［J］. The Chemical Engineering Journal， 1990， 44（1）： 1-9.

［6］ MOSTOUFI N， CHAOUKI J. Local solid mixing in gas-solid fluidized beds ［J］. Powder Technology， 2001， 114（1）： 23-31.

［7］ DU B， FAN L S， WEI F， et al. Gas and solids mixing in a turbulent fluidized bed ［J］. AIChE Journal， 2002， 48（9）： 1896-1909.

［8］ 朱建新， 马增益， 池涌， 等. 图像法用于流化床颗粒运动速度测量的实验研究［J］. 计量学报， 2004， 25（2）： 142-145. ZHU J X， MA Z Y， CHI Y， et al. Experimental research on fluidized bed particle velocity field measurement with imaging processing ［J］. Acta Metrologica Sinica， 2004， 25（2）： 142-145.

［9］ 严建华， 朱建新， 马增益， 等. 图像法用于流化床颗粒混合特性的研究［J］. 高校化学工程学报， 2006， 20（5）： 745-751. YAN J H， ZHU J X， MA Z Y， et al. Research on mixing character of fluidized bed particles with image processing technique ［J］. Journal of Chemical Engineering of Chinese Universities， 2006， 20（5）：745-751.

［10］ 罗娅， 马增益， 朱建新， 等. 图像追踪算法用于流化床颗粒横向混合特性的研究［J］. 热力发电， 2006， 34（11）： 34-38. LUO Y， MA Z Y， ZHU J X， et al. Study on behavior of particles cross-mixing by using picture tracking algorithm ［J］. Thermal Power Generation， 2006， 34（11）： 34-38.

［11］ 南海明， 文尧顺， 吴秀章， 等. 甲醇制烯烃工业装置催化剂积碳特性模拟研究［J］. 石油化工， 2014， 43（1）： 79-86. NAN H M， WEN Y S， WU X Z， et al. Simulation of coking on catalyst in methanol to olefins plant ［J］. Petrochemical Technology，2014， 43（1）： 79-86.

［12］ PALLARES D， JOHNSSON F. A novel technique for particle tracking in cold 2-dimensional fluidized beds — simulating fuel dispersion ［J］. Chemical Engineering Science， 2006， 61（8）：2710-2720.

［13］ 刘道银， 陈晓平， 陆利烨， 等. 流化床密相区颗粒扩散系数的CFD数值预测［J］. 化工学报， 2009， 60（9）： 2183-2190. LIU D Y， CHEN X P， LU L Y， et al. Prediction of solids dispersion coefficient in fluidized bed dense zone using CFD simulation ［J］. CIESC Journal， 2009， 60（9）： 2183-2190.

［14］ 翁文国， 廖光煊， 王喜世. 基于互相关的DPIV图像诊断方法研究［J］. 实验力学， 1999， 14（3）： 323-329. WENG W G， LIAO G X， WANG X S. A diagnosing method by DPIV based on cross-correlation algorithm ［J］. Journal of Experimental Mechanics， 1999， 14（3）： 323-329.

［15］ 翁文国， 廖光煊. DPIV图像的诊断方法研究［J］. 火灾科学， 1999，8（4）： 1-7. WENG W G， LIAO G X. Investigation of the interrogation method of pictures in DPIV ［J］. Fire Safety Science， 1999， 8（4）： 1-7.

［16］ WILLERT C E， GHARIB M. Digital particle image velocimetry ［J］. Experiments in Fluids， 1991， 10（4）： 181-193.

［17］ WESTERWEEL J， DABIRI D， GHARIB M. The effect of a discrete window offset on the accuracy of cross-correlation analysis of digital PIV recordings ［J］. Experiments in Fluids， 1997， 23（1）：20-28.

［18］ ADRIAN R J， WESTERWEEL J. Particle Image Velocimetry ［M］. Cambridge： Cambridge University Press， 2011.

［19］ RAFFEL M， WILLERT C E， KOMPENHANS J. Particle Image Velocimetry： a Practical Guide ［M］. Berlin： Springer， 2013.

［20］ THIEL W J， POTTER O E. The mixing of solids in slugging gas fluidized beds ［J］. AIChE Journal， 1978， 24（4）： 561-569.

［21］ GELDART D. Gas Fluidization Technology ［M］. England：Wiley-Interscience Publication， 1986： 97.

［22］ 陈曦， 钟文琪， 陆勇， 等. 基于光纤内窥镜和高速摄影联用测量喷动床颗粒速度研究［J］. 工程热物理学报， 2013， 34（2）： 278-281. CHEN X， ZHONG W Q， LU Y， et al， Measurement of particle velocity in spouted bed based on the combination of fiberscope and high-speed photography ［J］. Journal of Engineering Thermophysics，2013， 34（2）： 278-281.

Diffusion coefficient of solid particles in turbulent fluidized bed

ZHOU Bihui1， ZHAO Ming2， LIANG Junyu2， LU Yong1， XIAO Rui1
（1Key Laboratory of Energy Thermal Conversion and Control of Ministry of Education， Southeast University， Nanjing 210096，Jiangsu， China；2Electric Power Research Institute， Yunnan Electric Power Test and Research Institute， Kunming 650217，Yunnan， China）

Based on particle image velocity （PIV） technology and particle diffusion law， the diffusion coefficient of SAPO-34 catalyst particles in turbulent fluidized bed for methanol to olefins （MTO） was studied. A two dimensional transparent glass fluidized bed reactor was used to study the particle diffusion coefficient as functions of operating gas velocity and particle size. The motion of SAPO-34 particles was recorded by high speed camera，based on which both longitudinal and lateral velocities were calculated via image processing technology， hence the diffusion coefficient was obtained according to particle diffusion law. It showed that both longitudinal and lateral diffusion coefficient of SAPO-34 particles （Geldart A） increased with operating gas velocity. The longitudinal diffusion coefficient ranged from 10-3m2·s-1to 10-2m2·s-1， and the lateral diffusion coefficient from 10-1m2·s-1to 10-2m2·s-1. In addition， under the same fluidization operating gas velocity， the particles with smaller particle size possessed larger diffusion coefficient than those with larger one. It is of significance for the research related to the motion law of particles in turbulent fluidized bed.

turbulence； fluidization； PIV； diffusion coefficient； MTO

date： 2015-09-24.

Prof. XIAO Rui， ruixiao@seu.edu.cn

supported by the National Natural Science Foundation of China （91334205）.

10.11949/j.issn.0438-1157.20151492

TQ 13

A

0438—1157（2016）05—1741—07

2015-09-24收到初稿，2015-12-12收到修改稿。

联系人：肖睿。第一作者：周弼辉（1989—），男，硕士研究生。

国家自然科学基金项目（91334205）。