考虑颗粒旋转的流化床流动和气化反应模拟

王志宇，郝振华，董立波，李俊国，陆慧林

（1中国科学院山西煤炭化学研究所，山西 太原 030001；2哈尔滨工业大学能源科学与工程学院，黑龙江 哈尔滨 150001）



考虑颗粒旋转的流化床流动和气化反应模拟

王志宇1，郝振华1，董立波1，李俊国1，陆慧林2

（1中国科学院山西煤炭化学研究所，山西 太原 030001；2哈尔滨工业大学能源科学与工程学院，黑龙江 哈尔滨 150001）

摒弃传统颗粒动力学模型中颗粒绝对光滑的假设，以粗糙颗粒为研究对象，同时考虑颗粒碰撞过程中的对心和切向分力建立了粗糙颗粒动力学模型，采用近似求解给出了相关本构关系式。结合粉煤气化反应模型模拟研究了鼓泡流化床内粉煤颗粒的流动-反应过程，获得了床内粗糙颗粒时均速度和浓度的径向分布。与光滑颗粒的计算结果相比，粗糙颗粒的脉动能量增大，床内不均匀特性进一步增强。同时得到的各气体组分的浓度分布与他人的实验结果相吻合。

流化床；动力学模型；颗粒碰撞；颗粒旋转；数值模拟

DOI：10.11949/j.issn.0438-1157.20151663

鉴于此，一些科研工作者对颗粒动力学模型进行了修正。Lun［18］、Jenkins等［19］将颗粒运动分解为平动和旋转运动，采用弹性恢复系数、切向弹性恢复系数和摩擦系数描述粗糙颗粒碰撞过程，通过引入颗粒旋转动量和旋转脉动能量方程，针对粗糙颗粒建立了颗粒动力学模型。但由于该模型额外增加了颗粒角动量和旋转脉动能量守恒方程，导致数值计算过程中稳定性和收敛性下降。Goldschmidt等［20］对颗粒碰撞进一步分析，引入有效弹性恢复系数对能量耗散率进行简化计算。虽然简化模型在方程形式上与光滑颗粒动力学模型具有一致性，但由于未计入颗粒旋转对颗粒表面摩擦力的影响，实际上低估了颗粒间摩擦能量耗散。本研究考虑颗粒平动和旋转运动的总能量传递和耗散，通过引入颗粒平动和旋转拟总温eo建立同时考虑颗粒平动和旋转的颗粒拟温度方程，结合反应动力学数据模拟重现流化床内的气体-颗粒的流动和气化反应过程。

1　计算数学模型

1.1守恒方程及粗糙颗粒动力学模型

假设固体颗粒为球形且直径和物性相同；颗粒为准刚性颗粒，在碰撞前后形状不发生变化；颗粒碰撞只发生在两个颗粒之间，对于3个及3个以上颗粒之间的碰撞不予考虑；碰撞为点接触，而且碰撞产生瞬时冲力，忽略碰撞瞬时其他外力作用。则颗粒相质量和动量方程可由输运理论得出

其中，Sgs和Ssg分别为气体和固体单位时间单位体积内生成的质量。P为颗粒相总应力，由悬浮应力Pk和碰撞应力Pc组成，即P=Pk+Pc。

取物理量φ=0.5mc2+0.5Iω2，代入Maxwell输运方程可得颗粒脉动拟总温方程

式中，eo为颗粒拟总温；q为颗粒相热流通量，由颗粒平动和旋转作用下的悬浮动力效应qk和碰撞效应qc组成。

从式（4）可以看出颗粒拟总温同时表征颗粒平动和转动两种速度脉动强弱。当不考虑颗粒旋转运动时（即W=0），颗粒拟总温仅表征平动拟温度，模型可回归到光滑颗粒动力学模型。当考虑颗粒旋转运动时，能量分配扩展到转动自由度，也就是说在颗粒碰撞过程中颗粒平动和转动之间可以交换能量。

模型本构关系式可通过近似法求解［21］，其结果见式（5）～式（14）。可见，引入颗粒旋转后上述方程式（1）～式（3）其本身形式不发生改变，引入对颗粒旋转的考虑后改变了本构关系式的表达。

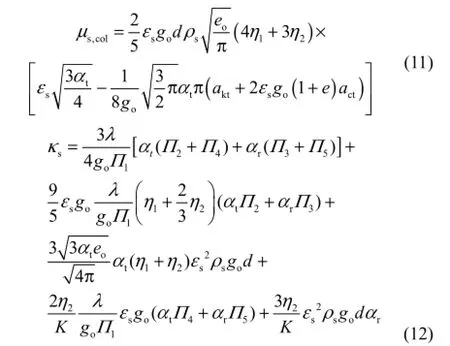
1.2组分和能量方程

气体内各组分之间以及气体组分与固体组分之间相互反应，从而产生组分之间的质量转移。

气相组分方程表示为

式中，i=1～Ng，Yg，i、Jg，i分别为组分i的局部质量分数和扩散通量，扩散通量可根据Fick定律计算。

对于计算区域壁面为绝热的情况，根据能量守恒定律，气相和固相的能量守恒方程为

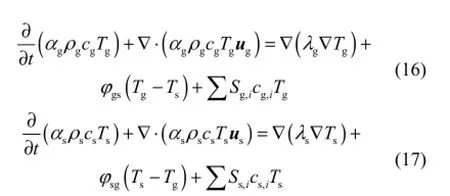
式中，T、c、λ、φgs分别表示温度、比热容、热导率和相间传热系数；ScT表示能量源项。

式中，cg，i、cs，i分别为气相和固相组分i的比热容，按以温度为变量的多项式回归方程计算。

气体混合物传热系数的计算建立在分子运动论的基础上。

1.3煤气化中的热解反应

采用同时考虑低温和高温的双方程煤气化热解模型。

挥发分的产生由式（22）、式（23）中两部分共同控制，在低温时前部分起主导作用，在高温时后部分起主导作用。

挥发分的产生速率r0为

式中，γ为固体碳颗粒未反应的浓度。

1.4异相反应

煤逸出挥发分后剩余的固体为固定碳和灰分组成的均匀混合物，称为残炭。残炭中的灰分化学性质稳定，不与其他物质反应，因此煤气化过程中的非均相反应主要是固定碳在气相氧化剂（氧气、二氧化碳和水汽）中发生氧化反应。

表1　R 均相化学反应速率Table 1 Homogeneous reaction rates used in simulations

式中， κ=2512exp（-6204/T）为CO与CO2的化学计量比。

假定残炭颗粒为球形且粒径不发生变化，按缩核模型计算气化过程中非均相反应的反应速率。

式中，ri为式（26）～式（28）中的气相组分i（i=O2，H2O，CO2）的消耗速率，kg·m-3·s-1；pi为气相组分i的分压力，Pa。

由式（29）可以看出，缩核模型的反应速率主要由外部扩散系数kf，i、灰层扩散系数ka，i和表面反应系数kr，i三者共同控制。

外部扩散系数kf，i由式（30）给出

式中，Di为气相组分i的扩散系数，m2·s-1；Ri为气相组分i的气体常数，J·mol-1·K-1；Ts为颗粒温度，K；Shm与Sc分别为Sherwood数和Schmidt数。

灰层扩散系数ka，i由式（32）求解

式（26）～式（28）中表面反应系数kr，i（Pa-1·s-1）分

别为

1.5均相反应

均相反应指气体各组分之间的相互反应。煤气化过程的主要的均相反应如下所示，均相反应式（37）～式（40）的化学反应速率见表1。

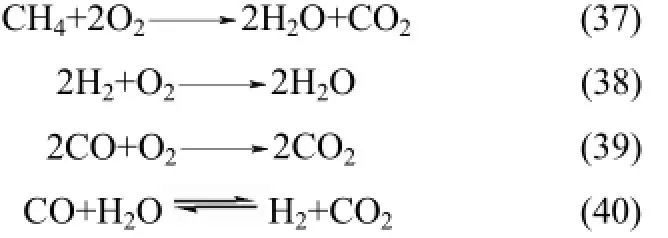
2 数值计算条件

本研究以Chejne等［22］搭建的鼓泡流化床气化炉实验台为计算对象（图1），在Mfix平台上采用有限元离散格式和SIMPLE算法对所建模型进行求解。固体煤颗粒工业分析、元素分析及热值见表2，其余模拟参数见表3。

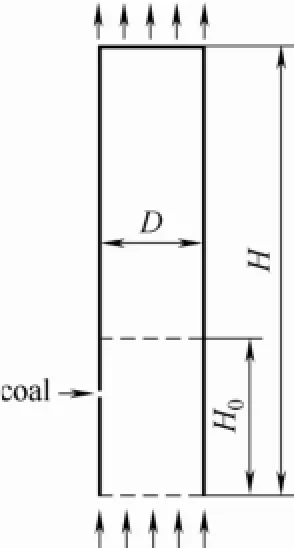
图1　流化床气化床结构Fig.1　Structure scheme of 2D fuel reactor

表2　R固体煤颗粒特性分析Table 2　Characteristics of coal solids

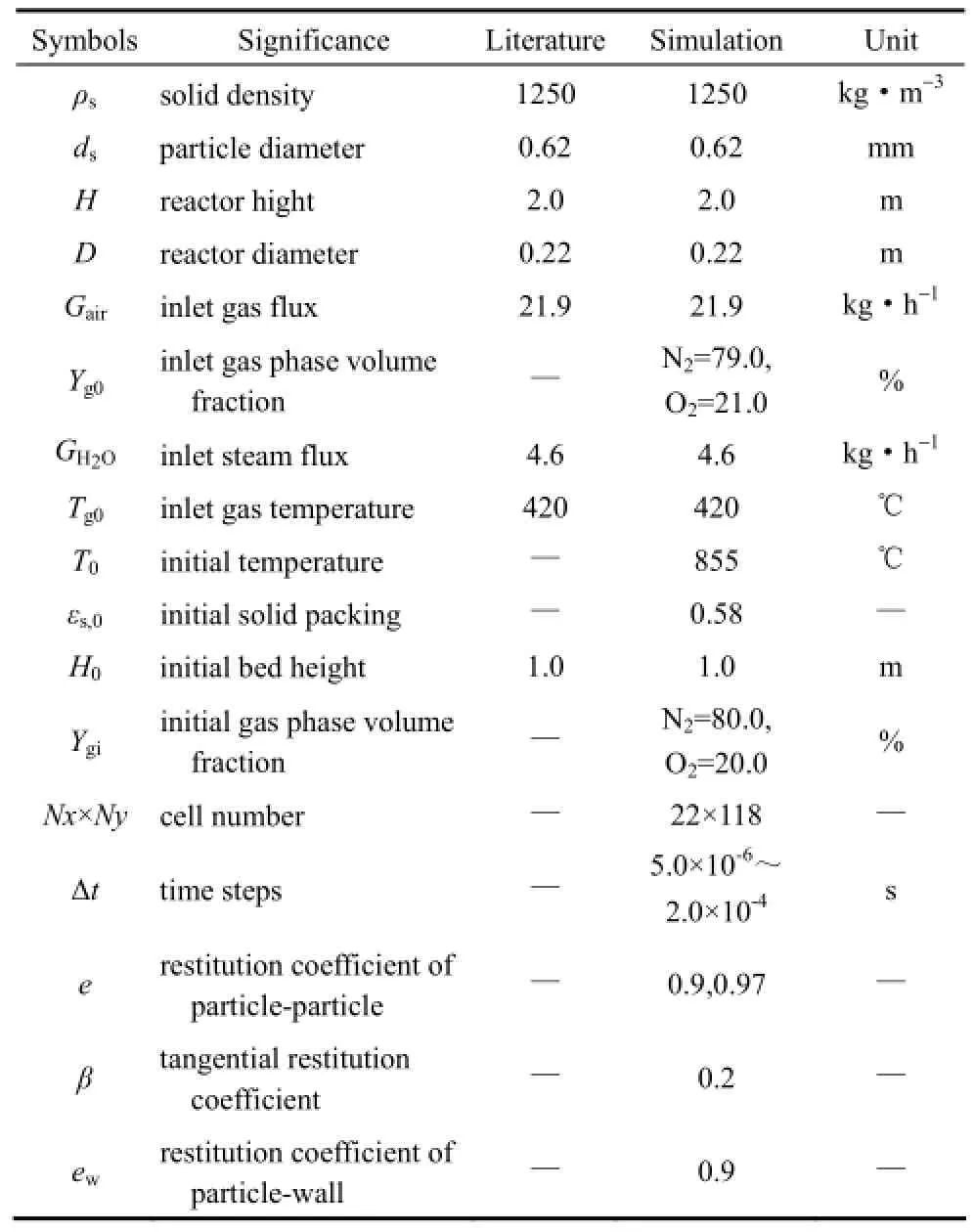
表3　RChejne等［22］的实验参数及数值模拟参数Table 3　Parameters used for Chejne et al［22］and simulations

3　计算结果及分析

3.1模拟结果与实验结果对比

图2　模拟结果与实验结果Fig.2　Comparisons between predictions and experimental data

图2给出了不同入口温度下计算结果和实验结果。通过对比可以发现，计算值中二氧化碳和氢气的值偏大，一氧化碳的值偏小。模拟和实验的偏差可能由以下两方面引起：①实际实验过程中发生了碳酸钙、二氧化硫和氧气的反应，但由于发生量较小而在计算过程中没有引入相关反应方程；②煤气化热解模型的局限性。由于煤粉组成的复杂性，目前还没有一种准确的煤气化热解过程模型描述煤粉的煤气化过程。模拟结果与Yu等［23］采用KTGF模型的模拟结果具有相同的趋势。

图3为气化床内气体时均径向温度分布。由图可见，在气化炉入口位置（1.0～9.0 cm）氧气与煤颗粒、可燃气体（CO，H2，CH4）发生剧烈的燃烧反应，导致气体具有较大的温升梯度。这表明氧气在进入气化炉后很快就被消耗掉，床内上部以还原性气氛为主。在距入口高度11.0 cm处氧气基本被耗尽，温度梯度变化趋缓，随后受到还原反应的影响温度又部分回落。图中同时给出了考虑辐射换热模型 （P1模型） 时的温度分布模拟结果，可以看出考虑辐射换热后床内的换热量增强，致使床内温度沿径向分布更为均匀。与KTGF模型的计算结果相比［23］，采用KTRF模型后入口处温度梯度减小，这可能是由于模型引入颗粒旋转后增强了颗粒浓度分布的不均匀性，从而导致温度梯度减小。Chejne等［22］给出了床内温度沿轴向的分布曲线，本模拟获得了相似的结果（见图3右上角）。

图3　气相径向和轴向温度时均分布Fig.3　Time-averaged profile of simulated temperature

3.2粗糙颗粒对宏观和微观流动特性的影响

图4为分别采用KTRF和KTGF计算得到的瞬时颗粒浓度分布。相较于KTGF，当采用KTRF时乳化相内颗粒聚集作用更为明显，乳化相中KTRF计算浓度更高，而在气泡内部KTRF模型颗粒浓度较小，气泡与乳化相的界限更为明显，同时气泡直径变大，模拟得到的床层高度较高。可见，KTRF由于考虑颗粒的旋转和粗糙特性，增加了颗粒间非弹性碰撞产生动量和能量的传递和耗散，致使整个床层内的气固不均匀性分布更为明显。

图4　颗粒相瞬时浓度分布Fig.4　Instantaneous particle concentration distribution

图5为分别采用KTRF和KTGF计算得到的颗粒脉动能量随颗粒浓度的变化规律。Gidaspow等［24］采用CCD高速摄影方式实验研究了床内颗粒拟温度随浓度的变化趋势，实验结果表明颗粒拟温度随浓度呈先增大后减小的趋势，本研究获得了相同的趋势。从图中可见，在低浓度区域，由于颗粒浓度低，颗粒间相互碰撞频率小，颗粒旋转对颗粒碰撞项的贡献几乎可以忽略不计，因此两种模型计算得到的颗粒脉动能量基本一致。但随着浓度的升高，颗粒间相互碰撞频率升高，由于KTRS模型包含颗粒转动脉动能量，其脉动能量明显大于仅考虑颗粒平动脉动能量的KTGF模型计算结果。

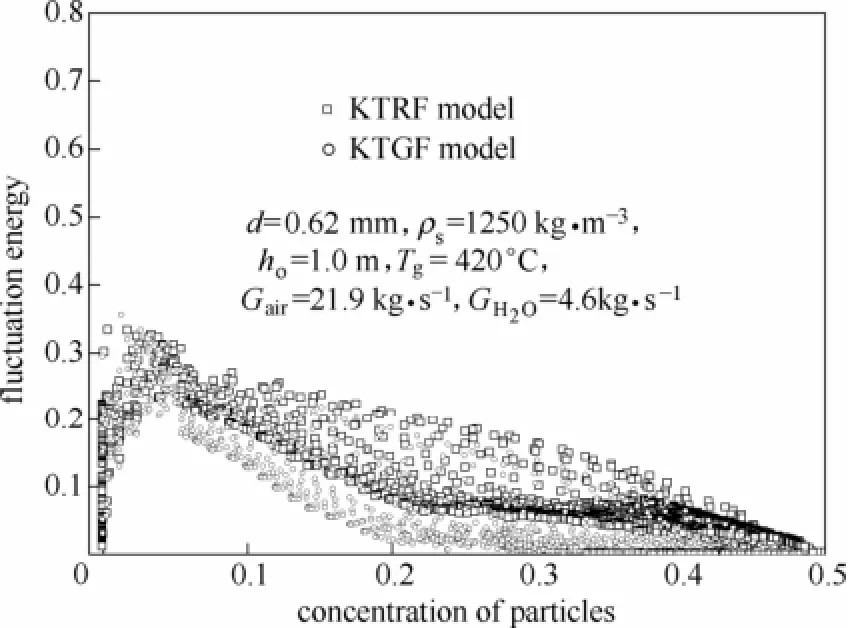
图5　颗粒脉动能量随颗粒浓度的变化规律Fig.5　Fluctuation energy distribution

3.3颗粒浓度和速度径向分布

图6为采用不同颗粒弹性恢复系数模拟得到的各床高下颗粒时均浓度沿床层径向的分布。可以看出各床高颗粒浓度沿床层径向呈现中心浓度低边壁浓度高的分布趋势。在床高为20 cm的床层径向截面上，受分布板影响以及此处剧烈的气化反应对固体颗粒的搅拌作用，在此床高下颗粒浓度变化幅度较小，在径向方向上浓度分布较为平缓。随着高度的上升，由于受到气泡间相互汇集、压力变化以及气化反应释放气体等作用的影响，气泡直径逐渐变大，在床层中心区域颗粒浓度变小，颗粒浓度变化幅值增大。对于不同的颗粒弹性恢复系数而言，从图6可以看出，当颗粒弹性恢复系数为0.90时，边壁区域的颗粒浓度更高。

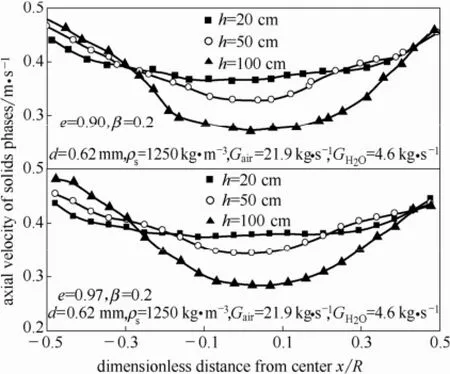
图6　颗粒时均浓度径向分布Fig.6　Profile of simulated concentration of particles

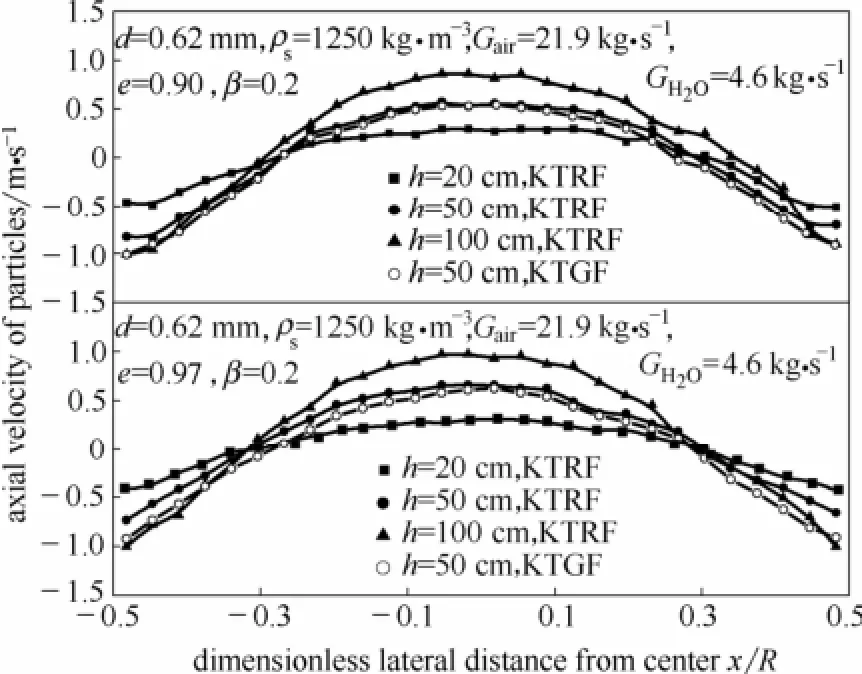
图7　颗粒时均速度径向分布Fig.7　Profile of simulated velocity of particles

图7为颗粒弹性恢复系数分别为0.90和0.97时不同床高下颗粒时均速度沿床层径向的分布。可以看出各床高下颗粒速度表现为：在床中心区域颗粒向上流动，在床壁面区域颗粒向下流动。图中同时给出了高度50 cm时采用Johnson摩擦应力的计算结果。从图中可以看出，考虑颗粒摩擦作用后气体给予颗粒的能量一部分被颗粒摩擦作用消耗，导致颗粒速度下降。对比图7上、下两图可以发现，对于不同的颗粒弹性恢复系数而言，当弹性恢复系数较小时颗粒碰撞能量耗散较大，致使颗粒在边壁区域下降速度增大，在中心区域上升速度增大。

4　结　论

针对粗糙颗粒，采用弹性恢复系数和切向弹性恢复系数描述颗粒碰撞过程，引入颗粒拟总温表征颗粒平动和旋转速度脉动，并基于输运理论给出颗粒拟总温守恒方程，建立了颗粒碰撞过程中平动和旋转运动共同作用的粗糙颗粒动力学模型，给出了粗糙颗粒相压力、黏度等输运参数计算模型，结合反应动力学参数，以Chejne等［22］实验台为模拟对象，数值模拟再现了鼓泡流化床内的粗糙颗粒流动和反应过程。模拟结果显示考虑颗粒粗糙特性和旋转运动后床内颗粒的气固不均匀性进一步加剧，同时模拟得出的气体组分分布与实验结果相吻合。

References

［1］ 陶贺， 钟文琪， 张勇， 等. 不同颗粒物性对异径混合非球形颗粒分离特性影响的数值模拟［J］. 动力工程学报， 2015， 31（8）： 652-658. TAO H， ZHONG W Q， ZHANG Y， et al. Effects of particle properties on separation behavior of differently-sized non-spherical particle mixtures ［J］. Journal of Chinese Society of Power Engineering， 2015，31（8）： 652-658.

［2］ 谭骏华， 罗坤， 樊建人. 软球模型在颗粒流全尺度模拟中的验证和分析 ［J］. 浙江大学学报（工学版）， 2015， 49（2）： 344-350. TAN J H， LUO K， FAN J R. Verification and analysis of soft-sphere model in fully-resolved simulation of particulate flow ［J］. Journal of Zhejiang University（Engineering Science）， 2015， 49（2）： 344-350.

［3］ 周新宇， 高金森， 徐春明， 等. 颗粒碰撞恢复系数对循环流化床提升管内气固流动模拟的影响 ［J］. 石油化工， 2012， 41（5）： 551-555. ZHOU X Y， GAO J S， XU C M， et al. Effects of particle-particle restitution coefficients on the simulation of gas-solids flow in a circulating fluidized bed rise ［J］. Petrochemical Technology， 2012，41（5）： 551-555.

［4］ 朱立平， 袁竹林， 闫亚明， 等. 固定床中丝状颗粒的传热传质特性［J］. 化工学报， 2012， 63（7）： 2051-2058. ZHU L P， YUAN Z L， YAN Y M， et al. Model of heat transfer in filamentous granular materials based on discrete element method ［J］. CIESC Journal， 2012， 63（7）： 2051-2058

［5］ 闫洁， 罗坤， 樊建人， 等. 稀疏两相射流中颗粒碰撞的数值模拟［J］. 化工学报， 2008， 59（4）： 866-874. YAN J， LUO K， FAN J R， et al. Numerical study of inter-collision in dilute two-phase jet ［J］. Journal of Chemical Industry and Engineering （China）， 2008， 59（4）： 866-874.

［6］ GIDASPOW D. Multiphase fow and fluidization： continuum and kinetic theory description［R］. Boston： Academic Press， 1994.

［7］ JENKINS J T， SAVAGE S B. A theory for the rapid flow of identical，smooth， nearly elastic， spherical particles ［J］. J. Fluid Mech.， 1983，130： 187-202

［8］ DING J， GIDASPOW D. A bubbling fluidization model using kinetic theory of granular flow ［J］. AIChE Journal， 1990， 36（4）： 523-538.

［9］ YANG N， WANG W， GE W， et al. Simulation of heterogeneous structure in a circulating fluidized-bed riser by combining the two-fluid model with the EMMS approach ［J］. Industrial & Engineering Chemistry Research， 2004， 43： 5548-5561.

［10］ NAREN P R， LALI A M， RANADE V V. Evaluating EMMS model for simulating high solid flux risers ［J］. Chemical Engineering Research and Design， 2007， 85（8）： 1188- 1202.

［11］ ZHOU W， ZHAO C S， DUAN L B， et al. CFD modeling of oxy-coal combustion in circulating fluidized bed ［J］. International Journal of Greenhouse Gas Control， 2011， 5（6）： 1489-1497.

［12］ XUE Q， FOX R O. Multi-fluid CFD modeling of biomass gasification in polydisperse fluidized-bed gasifies ［J］. Powder Technology， 2014，254： 187-198.

［13］ 骆仲泱， 吴学成， 王勤辉， 等. 循环流化床中颗粒旋转特性 ［J］.化工学报， 2005， 56（10）：1869-1874. LUO Z Y， WU X C， WANG Q H， et al. Particle rotation characteristics in CFB riser ［J］. Journal of Chemical Industry and Engineering（China）， 2005， 56（10）：1869-1874.

［14］ WU X C， WANG Q H， LUO Z Y， et al. Theoretical and experimental investigations on particle rotation speed in CFB riser ［J］. Chemical Engineering Science， 2008， 63（15）： 3979-3987.

［15］ WU X C， WANG Q H， LUO Z Y， et al. Experimental study of particle rotation characteristics with high-speed digital imaging system ［J］. Powder Technology， 2008， 181（1）： 21-30.

［16］ WU X C， WANG Q H， LUO Z Y， et al. Rotation speed measurement of moving particles in a CFB riser ［J］. Particuology， 2009， 7（4）：238-244.

［17］ DAVID G W， SATWINDER S S. CHARLES S C. Particle rotation as a heat transfer mechanism ［J］. International Journal of Heat and Mass Transfer， 1989， 32（8）： 1413-1423.

［18］ LUN C K K. Kinetic theory for granular flow of dense， slightly inelastic， slightly rough spheres ［J］. J. Fluid Mech.， 1991， 233：539-559.

［19］ JENKINS J T， RICHMAN M W. Kinetic theory for plane flows of a dense gas of identical， rough， inelastic， circular disks ［J］. Physics of Fluids， 1985， 28（12）： 3485-3494.

［20］ GOLDSCHMIDT M J V， BEETSTRA R， KUIPERS J A M. Hydrodynamics modelling of dense gas-fluidised beds： comparison of kinetic theory of granular flow with 3D hard-sphere discrete particle simulations ［J］. Chemical Engineering Science， 2002， 57（11）：2059-2075.

［21］ WANG S， HAO Z H， LU H L， et al. A bubbling fluidization model using kinetic theory of rough spheres ［J］. AIChE Journal， 2012， 58（2）：440-455.

［22］ CHEJNE F， HERNANDEZ J P. Modeling and simulation of coal gasification process in fluidized bed ［J］. Fuel， 2002， 81（13）：1687-1702.

［23］ YU L， LU J， ZHANG X P， et al. Numerical simulation of the bubbling fluidized bed coal gasification by the kinetic theory of granular flow （KTGF） ［J］. Fuel， 2007， 86（5/6）： 722-734.

［24］ GIDASPOW D， LU H L. Equation of state and radial distribution functions of FCC particles in a CFB ［J］. AIChE Journal， 1998， 44（2）：279-293.

Simulation of flow-reaction process in fluidized bed gasifier considering particle rotational motion

WANG Zhiyu1， HAO Zhenhua1， DONG Libo1，LI Junguo1， LU Huilin2
（1Institute of Coal Chemistry， Chinese Academy of Sciences， Taiyuan 030001， Shanxi， China；2School of Energy Science and Engineering， Harbin Institute of Technology， Harbin 150001， Heilongjiang， China）

Abandoning the pure smooth assumption of particles in classical kinetic theory of granular flow， this work established a kinetic theory model for rough granular and provided relevant constitutive correlations with approximate solutions by considering both opposite and tangential components force of the rough granular. Combined with the gasification model of coal powders， the flow-reaction process of coal powders was simulated in a bubbling fluidized bed and the time-average velocity and particle concentration distributions with rough granular were obtained in the bed. The simulated fluctuating energy and heterogeneity of rough granular in the fluidized bed increased compared with the simulated results of the smooth particles. The concentration of gas components obtained in the simulation agreed well with the experimental data in the literature.

fluidized bed； kinetic modeling； particle collision； particle rotation； numerical simulation

引　言

颗粒碰撞是流化床内动量、能量传递和交换的重要途径之一［1-5］。颗粒动力学模型（KTGF）以颗粒碰撞为基础，假设颗粒表面绝对光滑，在颗粒碰撞过程中仅考虑颗粒法向作用力，通过引入颗粒平动拟温度（θt=＜C2＞/3，C为颗粒平动脉动速度）实现模型的封闭［6-7］。自从Ding等［8］将颗粒动力学模型运用到流化床的研究以来，该模型随即被众多研究者采用。Yang等［9］、Naren等［10］考虑床内颗粒团聚体对气固曳力的影响，结合颗粒动力学模型模拟了提升管的气固流动特性。Zhou等［11］、Xue等［12］结合反应动力学数据研究了流化床内的燃烧和气化过程，获得了床内气体组分和温度分布。然而，实际流化床物料颗粒为粗糙颗粒，颗粒在相互瞬时碰撞过程中不仅产生法向作用力，同时产生切向作用力。切向作用力引发颗粒旋转运动，并改变颗粒间动量、能量的传递及耗散规律，继而影响流化床内气固流动、传递和反应特性。骆仲泱等［13］、Wu等［14-16］的研究表明粗糙颗粒相互碰撞引发颗粒旋转，旋转不仅会改变颗粒本身的运动轨迹，而且影响颗粒在床内的浓度和速度分布特性。David等［17］进一步揭示了颗粒旋转影响颗粒的传热传质特性。同时颗粒旋转导致其周围的气体组分浓度和温度梯度重新分配，影响气固相间反应特性。可见有必要在现有颗粒动力学模型中引入切向作用力及旋转运动的考虑。

date： 2015-11-04.

HAO Zhenhua， hzh@sxicc.ac.cn

supported by the National Natural Science Foundation of China（21506242） and the Shanxi Province Science Foundation for Youths（2014021014-7）.

TQ 53

A

0438—1157（2016）05—1725—07

2015-11-04收到初稿，2015-12-29收到修改稿。

联系人：郝振华。第一作者：王志宇（1976—），男，硕士研究生，助理研究员。

国家自然科学基金项目（21506242）；山西省青年科学基金项目（2014021014-7）。