一种组合型的深度学习模型学习率策略

贺昱曜　李宝奇



一种组合型的深度学习模型学习率策略

贺昱曜1李宝奇1

一个设计良好的学习率策略可以显著提高深度学习模型的收敛速度，减少模型的训练时间.本文针对AdaGrad和AdaDec学习策略只对模型所有参数提供单一学习率方式的问题，根据模型参数的特点，提出了一种组合型学习策略：AdaMix.该策略为连接权重设计了一个仅与当前梯度有关的学习率，为偏置设计使用了幂指数型学习率.利用深度学习模型Autoencoder对图像数据库MNIST进行重构，以模型反向微调过程中测试阶段的重构误差作为评价指标，验证几种学习策略对模型收敛性的影响.实验结果表明，AdaMix比AdaGrad和AdaDec的重构误差小并且计算量也低，具有更快的收敛速度.

深度学习，学习率，组合学习策略，图像重构

引用格式贺昱曜，李宝奇.一种组合型的深度学习模型学习率策略.自动化学报，2016，42（6）：953-958

深度学习［1-6］是机器学习领域一个新的研究方向，与传统的机器学习和信号处理方法相比，深度学习模拟人类视觉神经系统的层次体系，含有更多的隐含单元层，通过对原始数据逐层的非线性变换，可以得到更高层次的、更加抽象的特征表达，高层次的表达能够强化输入数据的区分能力，同时削弱不相关因素的不利影响.

深度学习凭借其处理复杂和不确定性问题的能力，在图像分类、文本检测、语音识别等领域取得了比以往方法更好的成绩［7］.成绩的提高是以规模更大、层次更深的网络结构为基础，以海量的训练数据为依据，以更多的调节参数为代价，所以深度学习模型的训练比以往的方法需要更长时间，因此如何加快模型的收敛速度是一个值得深入研究的问题.

一个呈下降趋势的学习率策略可以显著提高模型的收敛速度，减少模型的训练时间［8］.深度学习模型的学习率通常为常数型或简单呈下降趋势的指数型函数和幂指数型函数，其根据函数本身的特点调节学习率大小，在很多情况下上述方法仍然不失为一种最简单有效的学习率策略.2010年，Duchi等提出了自适应的全参数学习率策略AadGrad［9］，该方法为深度学习过程中每一个参数单独设计一个学习率，并利用梯度的平方和保证学习率的下降趋势，该方法首次提出全参数学习率策略，为深度学习模型的快速收敛提供了一个很好的解决思路.2013年，Senior等在AadGrad学习策略的基础上提出了一种改进型的学习策略AadDec［10］，该方法每个参数学习率由之前的所有回合梯度的平方和简化为当前梯度和上一回合梯度的平方和，并将该方法成功应用到语音识别系统中，在模型收敛速度上AadDec比AadGrad有进一步的提升.深度学习模型内连接权重和偏置属于两种类型的参数，作用也不一样，为不同类型的参数提供相同的学习策略是不合理的.

本文在AadGrad和AadDec学习策略的基础上，通过对随机梯度下降法收敛机制的分析以及对深度学习模型连接权重和偏置的深入研究，提出了一种组合型的学习策略AdaMix，即为连接权重和偏置分别设计学习率，以期能加快深度学习模型的收敛速度，同时减少模型的运算时间.

1　问题描述

本文以图像重构任务为背景，研究学习率对深度学习模型收敛性的影响.

1.1数据

为客观地评价学习率策略对深度学习模型收敛性的影响，实验采用MNIST数据库，该库总共包含70000幅28像素×28像素的图像，每一个样本为0～9的手写体数字，其中60000幅为训练样本集，10000幅为测试样本集.

1.2深度学习模型

本文研究的深度学习模型为Autoencoder［8］，从本质上讲它是深度信念网络（Deep belief nets，DBN）［11］的无监督形式，同样由多个限制玻尔兹曼机（Restricted Boltzmann machines，RBM）［12］逐层迭代组成.在预处理阶段（Pertraining），Autoencoder与DBN的训练方式一样，利用大量的无标签数据使模型参数的初值感知在一个合理的范围;在反向微调阶段（Fine-turning），DBN模型使用Wake-sleep算法［13］对模型的参数进行微调，而Autoencoder首先构建一个对称的网络用于生成原始输入数据，如图1所示，这个过程被称作展开（Unrolling），然后利用原始数据与生成数据之间的差异对模型的参数进行微调，整个过程不需要使用标签数据，经过足够多的迭代运算以后，模型便可以精确重构原始输入数据.

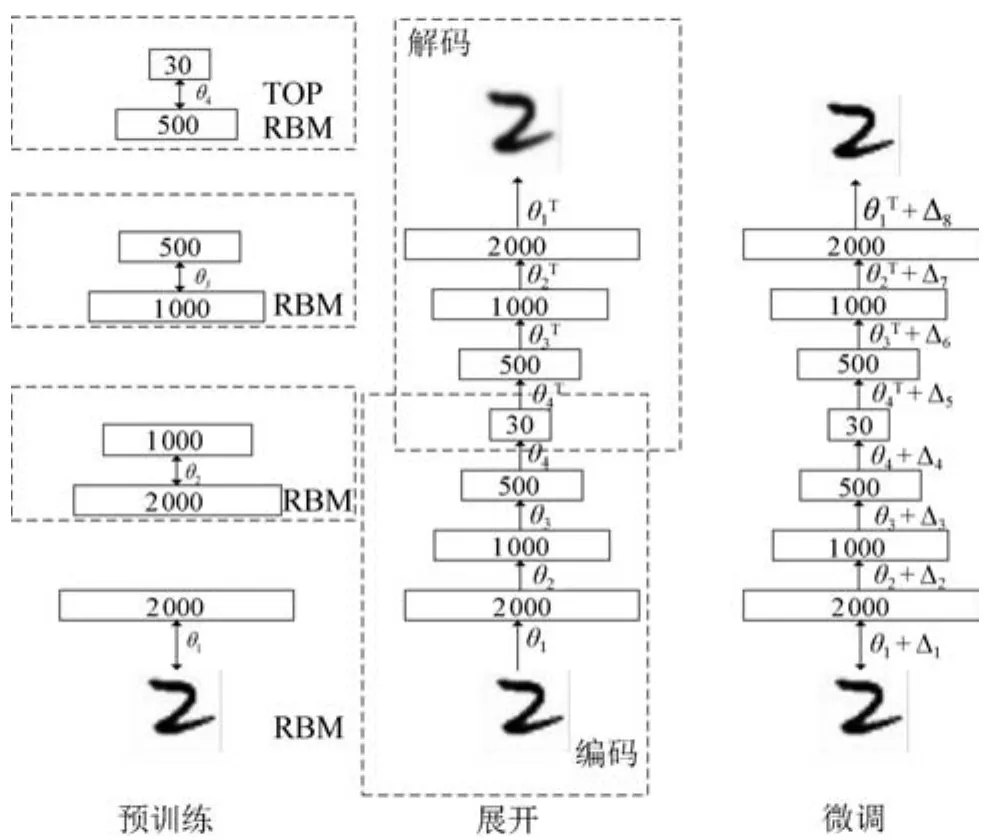
图1　Autoencoder模型的训练过程Fig.1　The training process of Autoencoder model

1.3学习率的定义

对于一个参数为θ=｛ωij，b1i，b2j｝的RBM模型，如图2所示，上层为隐含单元层，下层为可见单元层，可见单元与隐含单元之间双向连接，同一层内的神经元之间互不连接.从概率论的角度，这也就意味着在给定可见单元的状态下各个隐含单元之间是相互独立的，反之亦然.在模型训练过程中，需要计算三种不同类型的参数［14］.

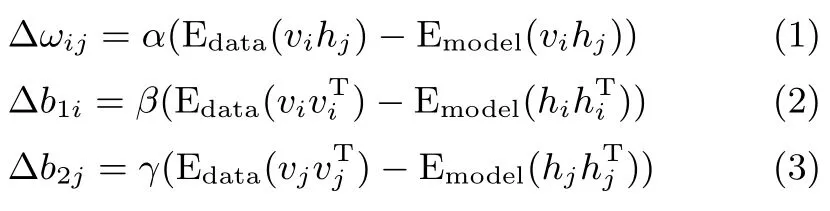
其中，α为可见单元层与隐含单元层之间连接权重的学习率，Δωij为权重增量;β为可见单元层偏置的学习率，Δb1i为偏置增量;γ为隐含单元层偏置的学习率，Δb2j为偏置增量. Edata为由输入数据得到的期望，Emodel为由模型得到的期望.η=｛α，β，γ｝称为模型的学习率.

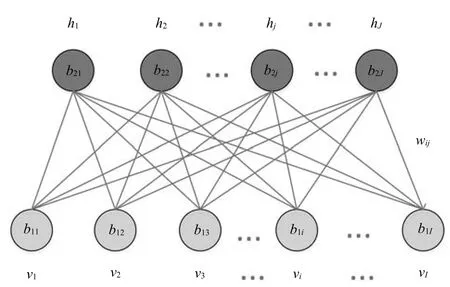
图2　RBM的结构图Fig.2　The network graph of an RBM

1.4随机梯度下降法

对于深度学习模型Autoencoder的参数θ优化求解问题［15-16］，其一般数学表达式为

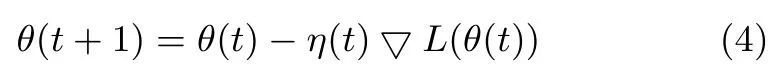
其中，L（θ）为定义在数据集上的损失函数，▽L（θ）为损失函数的梯度，θ（t+1）为迭代t+1时刻的参数值，θ（t）为迭代t时刻的参数值，η（t）为学习率（步长）.梯度下降法可以快速求解大多数优化问题，但对以大规模数据集（Large data set）为基础的深度学习模型参数优化而言，▽L（θ）的计算非常耗时甚至无法计算.

随机梯度下降法（Stochastic gradient descent，SGD）［17］是梯度下降法的变形.与梯度下降法计算整个数据集不同，SGD只在数据集中随机挑选一部分样本（Minibatch）来计算损失函数的梯度，其数学表达式为

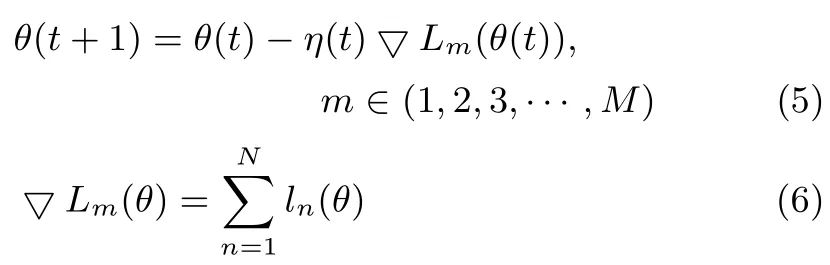
其中，▽Lm（θ）为利用第m个批次数据计算得到的损失函数梯度值，N为第m个批次数据集内样本的个数.与梯度下降法相比，SGD的计算量得到了极大的降低，所以深度学习模型主要采用SGD方法优化模型参数.

在满足

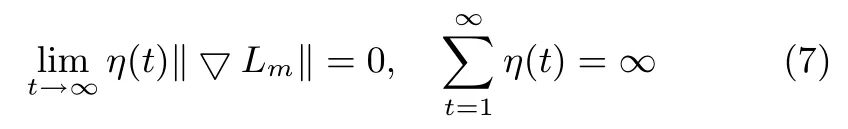
的条件下，SGD与梯度下降法具有相同的收敛特性［18］.‖▽Lm‖＜ H，H 为有界常数，模型的学习率需满足limt→∞η（t）=0，即一个呈下降趋势并收敛至0的学习率.

1.5评价指标

本文使用Autoencoder反向微调阶段测试数据集的重构误差（Reconstruction error rate，RER）作为模型收敛状态的定量评价指标.该指标是在像素的层次上描述图像的重构质量，与分类准确率相比能更好地描述模型参数的收敛状态.对于一个含有N个样本的测试数据集，其重构误差数学表达式为

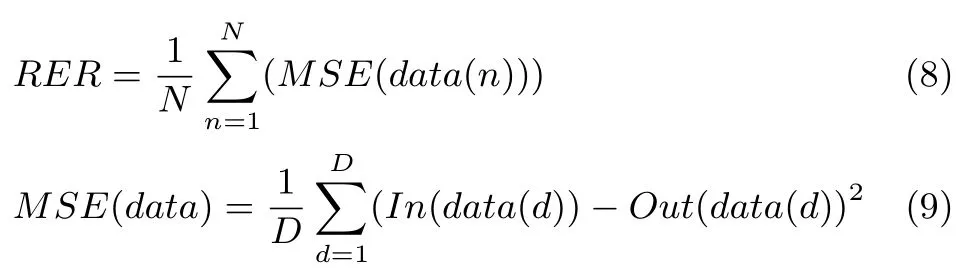
其中，MSE为均方误差（Mean squared error，MSE）的计算公式，In（data）为模型输入数据，Out（data）为模型生成数据，D为样本元素个数，即图像的像素数.在相同的迭代次数下，重构误差率越大收敛性越差，重构误差率越小收敛性越好.

2　学习率策略

常数型学习率在很多时候仍然不失为一种最简单有效的方法，但需要对学习率初值设置有足够丰富的经验.深度学习模型权重和偏置属于两种类型的参数，其作用也不同，因此在设计学习率策略时，需要考虑权重和偏置各自的特点.

2.1权重和偏置

深度学习模型的基本单元为神经元，其结构如图3所示.

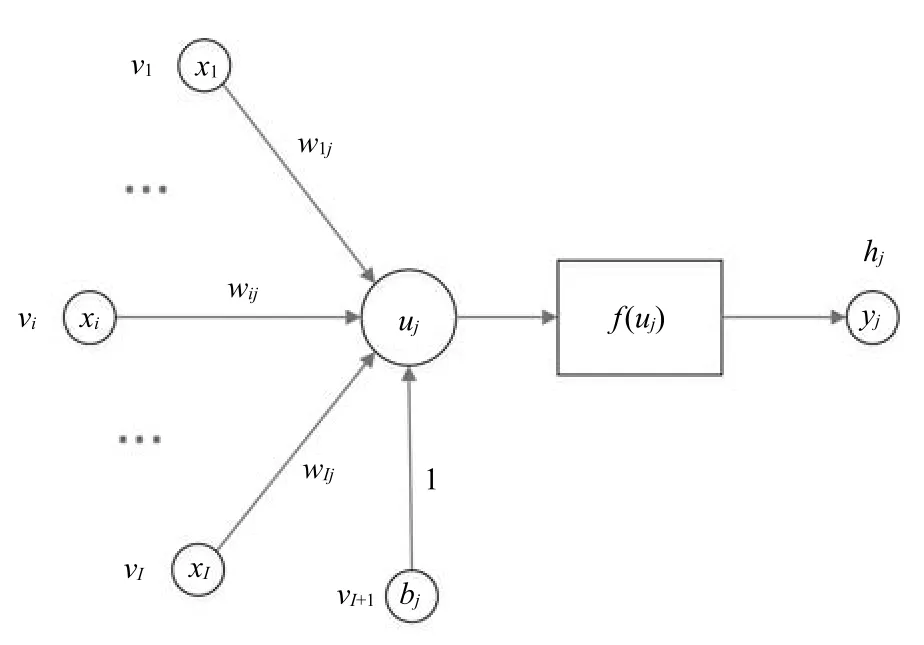
图3　人工神经元结构Fig.3　The network graph of an artificial neuron

图3中，vi代表输入神经元，xi为输入神经元状态，wij为输入神经元与输出神经元hj的连接权重，bj为输出神经元的偏置（阈值），f（·）为激活函数，yj为输出神经元状态.数学表达式如下：

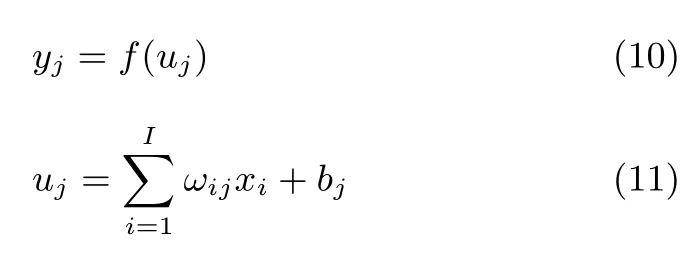
深度学习模型通过连接权重实现数据的表达，通过共享权重和偏置实现数据的区分，权重对深度学习模型的特征提取和逐层抽象非常重要;偏置项则是相当于原始数据增加的一个维度（一个状态为bj，权重一直为1的神经元），原始数据增加一个维度有利于数据的区分，尤其是在输入数据维度较低的条件下.但如果输入数据维度比较高，已经足以对数据进行区分，偏置的作用就会被弱化.因此对于本文的高维数据（本文数据维度为28像素×28像素），如果仅考虑连接权重而不考虑偏置，模型通过增加的迭代次数仍可达到它们同时作用的效果;反之则不然.

对于连接权重（权重）和偏置（状态）的调节需要采用不同的机制.对权重而言，为每个权重参数单独设计一个学习率，让其根据自身的状态自适应调节学习率及增量的大小，能加快输入数据的稳定表达，从而提高模型的收敛速度.虽然在处理高维数据时，偏置项的作用得到了弱化，但若处理不当仍会放慢模型收敛速度，所以偏置学习率的选取应在保证下降趋势的前提下，尽量选取计算量小的函数.后续的仿真实验对本文提出的权重和偏置学习率设计原则的合理性进行了验证.

2.2学习率策略

一个设计良好的学习率策略可以显著提高深度学习模型的收敛速度，减少模型的训练时间.全参数型学习率从机理上讲，更能加快深度学习模型的收敛速度.

2.2.1AdaGrad

AdaGrad是一个自适应的全参数形式学习策略.其数学表达形式如下：

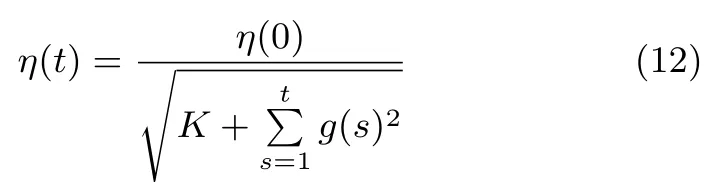
其中，η（0）为模型迭代第1次时的学习率，η（t）为模型迭代第t+1次时的学习率，g（s）为模型迭代第s次时的梯度（为了表述方便，用g代替▽Lm），K为常数项，通常K=1.

AdaGrad为模型连接权重和偏置的每个参数都单独提供了一个统一形式学习率，每个学习率能根据梯度的变化情况自适应调整大小，并利用梯度的平方和来保证学习率呈下降趋势.AdaGrad为研究全参数自适应学习率提供了依据.

2.2.2AdaDec

AdaDec是在AdaGrad的基础上针对语音识别系统提出的一种改进形式，分母中的梯度部分仅由上一回合和当前梯度决定，与之前的梯度没有关系，同时为了保证学习策略在长期的学习过程中呈现下降的趋势，分子用一个呈下降趋势的幂指数代替，其数学表达形式如下：

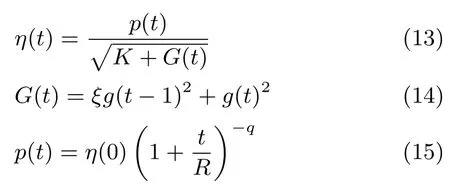
其中，p为幂指数型函数，R为最大迭代次数，q为常数项，通常取值为0.75;G（t）为当前梯度和上一次梯度的平方和，ξ为衰减因子，取值为0.999;K为常数项，取值为1.

AdaDec同样为模型连接权重和偏置的每个参数都单独提供了一个统一形式学习率，每个学习率在幂指数函数和最近两个回合梯度平方和的共同作用下自适应的下降.

2.2.3AdaMix

本文在AdaGrad和AdaDec的基础上，根据连接权重和偏置的不同特点和作用，依据本文提出的设计原则提出了一种组合形式的学习率策略：AdaMix，其数学表达式如下：

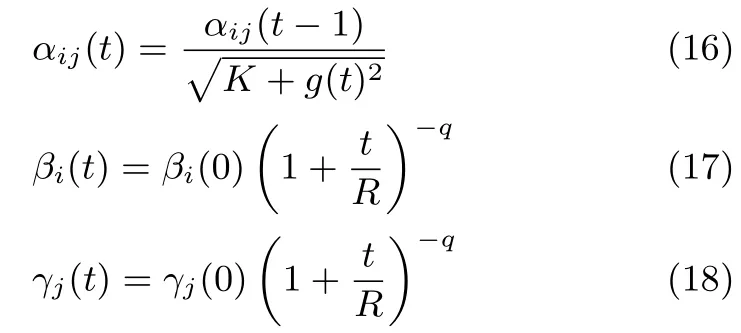
其中，αij（t）为连接权重下一回合的学习率，αij（t-1）为当前回合连接权重的学习率，g（t）2为当前回合的梯度的平方和，K=1.βi（t）和γj（t）分别为可见单元和隐含单元偏置的学习率，使用呈下降趋势的幂指数函数，q依然取0.75.

AdaMix权重部分的学习率是在AdaGrad和AdaDec两种学习率策略基础上做出的改进.在上一回合的学习率的基础上利用当前的梯度去自适应调节学习率的大小，这样设计的学习率更能准确描述模型的运行状态，调节得到的学习率也更合理，因此能加快模型的收敛速度，也减少了不必要的计算（历史梯度数据）.在处理高维数据时，偏置项的作用受到了弱化，因此在保证快速收敛的前提下，从减少计算量的角度出发，为偏置部分选择了幂指数函数作为学习率，同时所有的偏置项共用此学习率.

2.3算法分析

AdaGrad引入了过多的历史梯度数据，历史梯度数据对当前回合的学习率的贡献是有限的，而且当前学习率都是在初始学习率的调节基础上得到，并不能很好地反映模型运行状态.AdaDec是以幂指数函数作为学习率的下降趋势，在此基础上利用最近两个回合的梯度数据对当前学习率进行调节，而幂指数函数并不是模型真正的收敛曲线.AdaMix则是在充分考虑了模型参数特点的基础上，为权重设计了更能反映模型运行状态的学习率，为偏置设计了收敛速度较好但计算量小的幂指数函数，不同类型的参数依据自身的状态实现快速收敛.从模型的收敛条件来看，模型参数的学习率越能反映模型的运行状态越能加快模型的收敛速度.

3　仿真实验

为了验证本文方法AdaMix的性能，引入常数型学习率（Cons或Cons+Cons）作为参考，设计实验1对三种学习率策略AdaMix、AdaGrad和AdaDec的收敛性和计算量（模型运算时间）进行比较;为了验证本文提出的权重和偏置学习率设计原则，设计实验2、实验3和实验4分别研究权重和偏置的关系、不同学习率对权重的影响和不同学习率对偏置的影响;为了进一步验证本文方法的收敛性能，设计实验5研究不同规模数据量对本文方法（AdaMix）的影响.

实验采用一个5层的Autoencoder模型，第1层神经元的个数为784，第2层神经元的个数为1000，第3层神经元的个数为500，第4层神经元的个数为250，第5层神经元的个数为30，各层之间的初始连接权重服从均值为0、方差为0.001的高斯分布，第1层的初始偏置由训练数据决定，其他层的初始偏置设置为0.实验中所提到的方法均采用相同的学习率初始值，预处理阶段的学习率初始值为0.1，反向微调阶段的学习率初始值为0.001.模型的重构误差根据式（8）和式（9）计算.

3.1实验1.AdaMix的性能

实验比较常数型、AdaGrad、AdaDec和AdaMix四种学习率策略对深度学习模型收敛性的影响同时计算模型迭代50次时的运行时间.实验数据为完整MNIST数据集的1/10，即训练样本集为6000幅图像，测试样本集为1000幅图像.SGD迭代次数为5～50，步长为5.

从图4可以看出，四种学习策略都使模型的重构误差随迭代次数的增加而减小并且逐步趋于稳定.在整个迭代过程中常数型、AdaGrad和AdaDec的重构误差曲线接近，AdaMix的重构误差曲线低于另外三种.迭代次数为50次时，常数型学习率的重构误差为8.37，AdaGrad的重构误差为8.47，AdaDec的重构误差为8.22，AadMix的重构误差为7.82.AdaMix的收敛性能最好.

与此同时，模型迭代50次时计算机仿真时间依次为693.54s，810.20s，833.79s和752.56s.常数型学习率的计算时间最短，其次是AdaMix，AdaGrad和AdaDec.虽然迭代50次时，AadMix比常数型学习率的计算时间长，但从图4可以看出要实现相同的收敛效果，常数型学习率需要更多的迭代次数，即更长的计算时间.综合考虑重构误差和计算时间，AadMix的性能优于其他三种学习率.

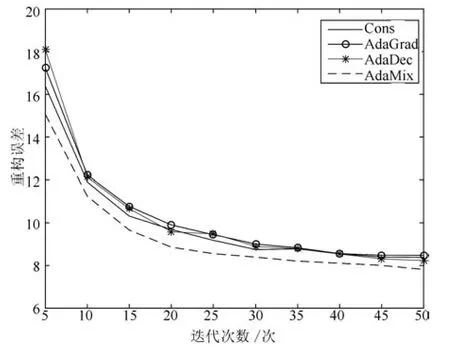
图4　AdaMix与其他三种方法的收敛性能比较Fig.4　Comparison of the convergence performance of AdaMix and other three methods

3.2实验2.权重和偏置的作用

本实验在常数型学习率策略（Cons+Cons）的基础上，设计另外两种形式的学习率策略.权重学习率为常数，偏置学习率为零（Cons+None）和权重的学习率为零，偏置的学习率为常数（None+Cons）.比较分析连接权重和偏置对深度学习模型收敛性的影响.实验数据为完整MNIST数据集的1/10，即训练样本集为6000幅图像，测试样本集为1000幅图像.SGD迭代次数为5～50，步长为5.

从图5可以看出，Cons+None和Cons+Cons两种学习率策略使模型的重构误差随着迭代次数的增加逐渐减小，并且下降的趋势是一致的，迭代50次时的重构误差分别为9.09和8.37;None+Cons型学习率策略并没有使模型的重构误差随迭代次数的增加而减少，而且一直保持在一个非常高的水平（51.40）.由此可见，在处理高维数据时（本文数据的维数28像素×28像素），权重对模型的收敛起决定性的作用，偏置的作用受到了弱化.同时通过增加迭代次数，Cons+None型学习率可以获得与Cons+Cons同样水平的重构误差.

图5　权重和偏置对深度学习模型收敛性的影响Fig.5　The influence of weight and bias on the convergence of deep learning model

3.3实验3.不同学习率对权重的影响

本实验在常数型学习率（Cons+Cons）的基础上，对权重部分设计五种不同形式的学习率策略.权重的学习率为指数（Exponent），偏置的学习率为常数（Exp+Cons）;权重的学习率为幂指数（Power），偏置的学习率为常数（Power +Cons）;权重的学习率为AdaGrad，偏置的学习率为常数（AdaGrad+Cons）;权重的学习率为AdaDec，偏置的学习率为常数（AdaDec+Cons）;权重为AdaMix的权重部分;偏置为常数型学习率（AdaMix+Cons）.比较上述六种学习率策略对深度学习模型连接权重的影响.实验数据为完整MNIST数据集的1/10，即训练样本集为6000幅图像，测试样本集为1000幅图像.SGD迭代次数为5～50，步长为5.

从图6可以看出，六种学习率策略都使模型重构误差随着迭代次数的增加而降低，整体趋势一致.模型迭代50次时常数型学习率重构误差为8.37，Exp+Cons型学习率为8.67，Power+Cons型学习率为8.38，AdaGrad+Cons型学习率为8.28，AdaDec+Cons型学习率为8.10，AdaMix +Cons型学习率为7.88.连接权重为全参数形式（后三种）的学习率策略比简单形式（前三种）的学习率策略具有更好的收敛性能，尤其是本文提出的权重学习方式.

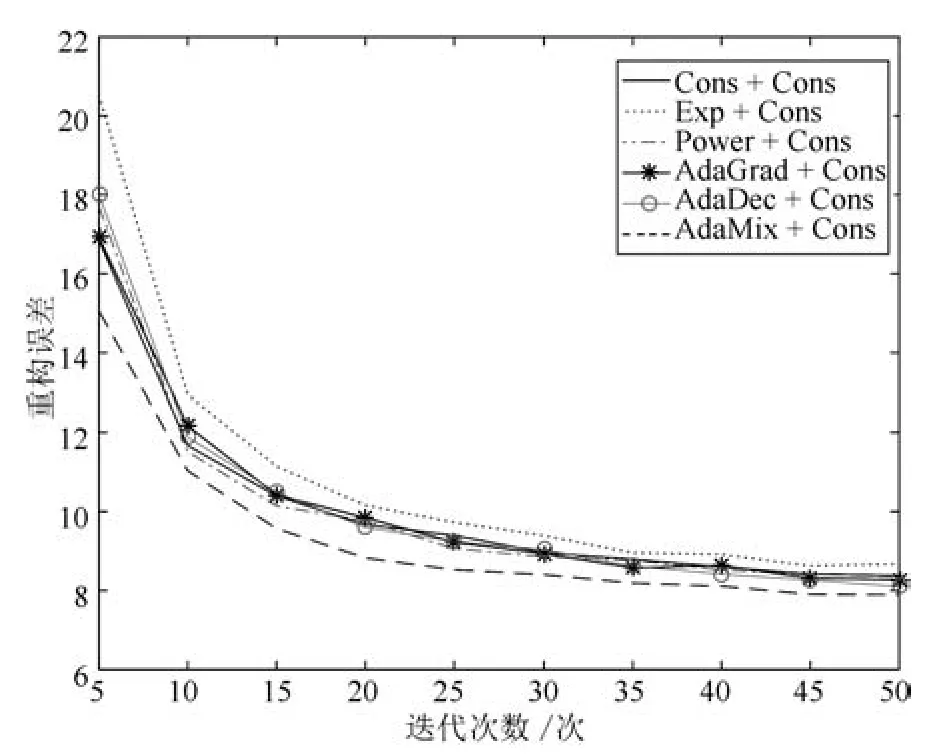
图6　不同学习率对深度学习模型权重的影响Fig.6　The influence of different learning rates on the weight of deep learning model

3.4实验4.不同学习率对偏置的影响

本实验在常数型学习率的基础上，对偏置部分设计五种不同形式的学习率策略.权重的学习率为常数，偏置的学习率为指数（Cons+Exp）;权重的学习率为常数，偏置的学习率为幂指数（Cons+Power）;权重的学习率为常数，偏置的学习率为AdaGrad（Cons+AdaGrad）;权重的学习率为常数，偏置的学习率为AdaDec（Cons+AdaDec）;权重的学习率为常数，偏置为AdaMix的权重部分的学习率（Cons+AdaMix）.比较上述六种学习率深度学习模型偏置的影响.实验数据为完整MNIST数据集的1/10，即训练样本集为6000幅图像，测试样本集为1000幅图像.SGD迭代次数为5～50，步长为5.

从图7可以看出，六种学习率策略都使模型重构误差随着迭代次数的增加而降低，整体趋势一致.六种偏置的学习率性能比较接近，模型迭代50次时常数型学习率的重构误差为8.37，Cons+Exp型学习率为8.49，Cons+Power型学习率为8.31，Cons+AdaGrad型学习率为8.54，Cons+AdaDec型学习率为8.44，Cons+AdaMix型学习率为8.45.六种学习略策略的收敛性能接近，偏置部分为幂指数形式的学习率时，模型收敛性能稍好.

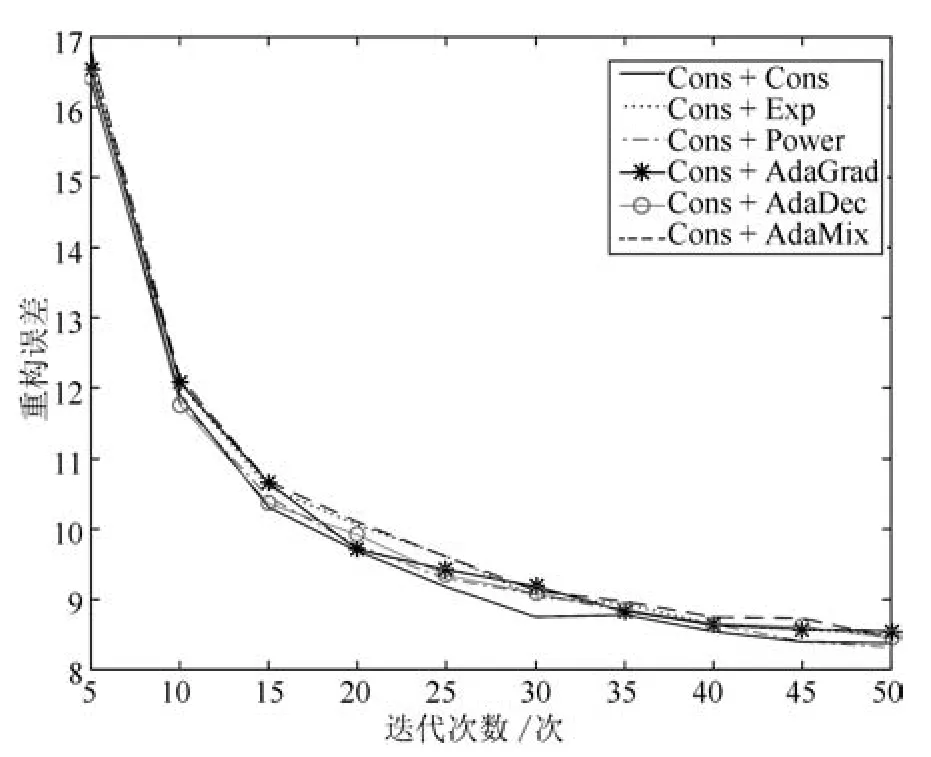
图7　不同学习率对深度学习模型偏置的影响Fig.7　The influence of different learning rates on the bias of deep learning model

3.5实验5.数据量对AdaMix性能的影响

本实验比较数据量对AdaMix性能的影响，数据量为完整MNIST数据集的1/10、3/10、6/10和1.SGD迭代次数为5～50，步长为5.

从图8可以看出，AdaMix在四种数据量下，模型重构误差随迭代次数的增大重构误差不断减小.模型迭代50次时四种数据量下的重构误差依次为7.81、5.06、4.06和3.56.在相同的迭代次数条件下，数据量越大模型的重构误差越小，收敛速度越快.

图8　不同数据量下的AdaMix对深度学习模型收敛性能的影响Fig.8　The convergence of deep learning model under AdaMix in different scale data sets

3.6讨论

简单形式的学习率（常数型、指数型和幂指数型等）虽然计算量低，但模型收敛速度慢.全参数形式的学习率策略（AdaGrad和AdaDec）虽然在一定程度上提高模型的收敛速度，但却提高了模型的计算量.AdaMix是一种组合型的学习率策略，即为权重和偏置分别设计符合各自特点的学习率，与AdaGrad和AdaDec相比，在提高模型收敛速度的同时也降低了模型的运算时间.收敛速度的提高得益于权重采用全参数形式的学习率，学习率的取值与模型当前的运行状态直接相关，所以得到的学习率更合理;计算量的降低一部分原因是权重部分减少了不必要的历史梯度计算，另外就是偏置采取了形式简单的幂指数函数作为学习率.当原始输入数据维度较高时，弱化了偏置的作用、强化了权重的作用，连接权重和偏置的关系和作用得到了进一步的理解.数据量对深度学习模型收敛有很大的影响，通过增加训练样本集的数量可以减小模型的重构误差、提高模型的收敛速度.

4　结论

通过对深度学习模型参数特点进行深入研究，给出了深度学习模型权重和偏置的设计原则，并在此基础上提出了一种组合型学习策略AdaMix，经实验证明AdaMix比Ada-Grad和AdaDec的收敛性好、计算量低.显然细化深度学习模型中参数的学习策略是提高模型是收敛性的有效手段.

在本文的研究基础上，拟开展的研究工作是：1）将本文方法应用到声音、文本等其他领域的学习过程中;2）对深度学习模型采用逐层的学习策略，并对本文方法做相应的改变.

References

1 Hinton G.Where do features come from？Cognitive Science，2014，38（6）：1078-1101

2 LeCun Y，Bengio Y，Hinton G.Deep learning.Nature，2015，521（7553）：436-444

3 Mnih V，Kavukcuoglu K，Silver D，Rusu A A，Veness J，Bellemare M G，Graves A，Riedmiller M，Fidjeland A K，Ostrovski G，Petersen S，Beattie C，Sadik A，Antonoglou I，King H，Kumaran D，Wierstra D，Legg S，Hassabis D. Human-level control through deep reinforcement learning. Nature，2015，518（7540）：529-533

4 Schmidhuber J.Deep learning in neural networks： an overview.Neural Networks，2015，61（7553）：85-117

5 Gao Ying-Ying，Zhu Wei-Bin.Deep neural networks with visible intermediate layers.Acta Automatica Sinica，2015，41（9）：1627-1637（高莹莹，朱维彬.深层神经网络中间层可见化建模.自动化学报，2015，41（9）：1627-1637）

6 Qiao Jun-Fei，Pan Guang-Yuan，Han Hong-Gui.Design and application of continuous deep belief network.Acta Automatica Sinica，2015，41（12）：2138-2146（乔俊飞，潘广源，韩红桂.一种连续型深度信念网的设计与应用.自动化学报，2015，41（12）：2138-2146）

7 Yu D，Deng L.Deep learning and its applications to signal and information processing.IEEE Signal Processing Magazine，2011，28（1）：145-154

8 Hinton G E，Salakhutdinov R R.Reducing the dimensionality of data with neural networks.Science，2006，313（5786）：504-507

9 Duchi J，Hazan E，Singer Y.Adaptive subgradient methods for online learning and stochastic optimization.The Journal of Machine Learning Research，2011，12：2121-2159

10 Senior A，Heigold G，Ranzato M A，Yang K.An empirical study of learning rates in deep neural networks for speech recognition.In：Proceedings of the 2013 IEEE International Conference on Acoustics，Speech，and Signal Processing. Vancouver，BC：IEEE，2013.6724-6728

11 Hinton G E，Dayan P，Frey B J，Neal R M.The“wake-sleep”algorithm for unsupervised neural networks.Science，1995，268（5214）：1158-1161

12 Hinton G E，Osindero S，Teh Y W.A fast learning algorithm for deep belief nets.Neural Computation，2006，18（7）：1527 -1554

13 Fischer A，Igel C.Training restricted Boltzmann machines：an introduction.Pattern Recognition，2014，47（1）：25-39

14 Salakhutdinov R，Hinton G.An efficient learning procedure for deep Boltzmann machines.Neural Computation，2012，24（8）：1967-2006

15 Robbins H，Monro S.A stochastic approximation method. The Annals of Mathematical Statistics，1951，22（3）：400-407

16 You Z，Wang X R，Xu B.Exploring one pass learning for deep neural network training with averaged stochastic gradient descent.In：Proceedings of the 2014 IEEE International Conference on Acoustics，Speech，and Signal Processing.Florence，Italy：IEEE，2014.6854-6858

17 Klein S，Pluim J P W，Staring M，Viergever M A.Adaptive stochastic gradient descent optimisation for image registration.International Journal of Computer Vision，2009，81（3）：227-239

18 Shapiro A，Wardi Y.Convergence analysis of gradient descent stochastic algorithms.Journal of Optimization Theory and Applications，1996，91（2）：439-454

贺昱曜西北工业大学教授.主要研究方向为智能控制与非线性控制理论，精确制导与仿真，信息融合，现代电力电子技术与功率变换理论.

E-mail：heyyao@nwpu.edu.cn

（HE Yu-YaoProfessor at Northwestern Polytechnical University.His research interest covers intelligent control and nonlinear control theory，precision guidance and simulation，information fusion，modern power electronics technology，and power transformation theory.）

李宝奇西北工业大学博士研究生.主要研究方向为目标检测、识别和跟踪，信息融合，深度学习.本文通信作者.

E-mail：bqli@mail.nwpu.edu.cn

（LI Bao-QiPh.D.candidate at Northwestern Polytechnical University.His research interest covers target detection，recognition and tracking，information fusion，and deep learning.Corresponding author of this paper.）

A Combinatory Form Learning Rate Scheduling for Deep Learning Model

HE Yu-Yao1LI Bao-Qi1

A good learning rate scheduling can significantly improve the convergence rate of the deep learning model and reduce the training time.The AdaGrad and AdaDec learning strategies only provide a single form learning rate for all the parameters of the deep learning model.In this paper，AdaMix is proposed.According to the characteristics of the model parameters，and a learning rate form which is only based on the current epoch gradient is designed for the connection weights，a power exponential learning rate form is used for the bias.The test reconstruction error in the fine-turning phase of the deep learning model is used as the evaluation index.In order to verify the convergence of the deep learning based on different learning rate strategies，Autoencoder，a deep learning model，is trained to restructure the MNIST database.The experimental results show that Adamix has the lowest reconstruction error and minimum calculation compared with AdaGrad and AdaDec，so the deep learning model can quickly converge by using AdaMix.

Deep learning，learning rate，combined learning scheduling，image reconstruction

10.16383/j.aas.2016.c150681

He Yu-Yao，Li Bao-Qi.A combinatory form learning rate scheduling for deep learning model.Acta Automatica Sinica，2016，42（6）：953-958

2015-10-20录用日期2016-04-01
Manuscript received October 20,2015；accepted April 1,2016
国家自然科学基金（61271143）资助
Supported by National Natural Science Foundation of China （61271143）
本文责任编委柯登峰
Recommended by Associate Editor KE Deng-Feng
1.西北工业大学航海学院 西安710072
1.School of Marine Science and Technology,Northwestern Polytechnical University,Xi′an 710072