基于FFT和小波变换阈值去噪的谐波检测方法
2016-08-22云凯周卓吴波
◎云凯 周卓 吴波
基于FFT和小波变换阈值去噪的谐波检测方法
◎云凯 周卓 吴波
由于噪声的存在严重影响电力系统谐波检测的精度,以及谐波检测时存在频谱泄漏、栅栏现象等,本文提出了基于快速傅里叶变换(FFT)和小波变换相结合改进阈值去噪的谐波检测方法。首先对信号进行小波变换,分析并除去非稳态谐波,然后采用FFT变换取出稳态谐波分量。在Matlab平台上对比FFT去噪、小波变换去噪和两者结合去噪效果,表明该方法谐波检测精度更高。
近年来,随着电力电子设备大量使用,电网的谐波污染越来越严重,严重降低了电能的生产、传输和利用效率。对谐波快速、准确的检测是谐波治理的关键技术。在实际应用中,信号中也存在大量的噪声,因此必须去噪是提高谐波检测精确度的重要前提。
对于整数次谐波检测常采用基于快速傅里叶变换(FFT)的方法,但对于非整数次谐波的检测,此方法没有局部分析的能力,也无法去除频带内的噪声;小波变换对于提取出的谐波信号存在频谱混叠以及窗口能量不集中的现象,为了解决上述问题,最终采用基于FFT和小波变换综合分析法对阈值去噪的谐波进行分析。
FFT和小波变换
FFT
FFT是根据离散傅氏变换特性以及算法而获得,它可以将一个信号变换到频域,本质是离散傅氏变换的快速算法,定义为:

连续傅里叶变换的逆变换 (inverse Fourier transform)为

其中:时间域函数f(t)为原函数,频率域函数F(ω)为傅里叶变换的像函数。
小波变换的基本原理
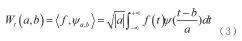
连续小波变换的优点:对于不同频段的高频滤波有良好的处理;适用于满足容许性条件的任何小波。
缺点:计算量大、信息冗余并且没有保持信号低频(包括直流)分量的低通滤波过程。
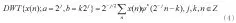
离散小波变换优点:简单、快速、信息非冗余等,缺点是丧失移动不变性。
本文采用FFT和小波变换结合的方法,具体步骤如下:首先对信号进行二进制离散小波变换,去除非稳态谐波分量,然后采用FFT变换取出稳态谐波分量。
阈值去噪的原理
在电网谐波检测中,低频信号一般为有用信号,高频信号为噪声信号,根据这个特点,阈值去噪的步骤如下:对信号进行小波分解,选取恰当的小波基且确定分解层数;对高频段的小波系数进行阈值处理;小波分解的N层低频系数和处理过的高频系数进行小波重构,目的是得出去噪后的信号。
利用MATLAB进行仿真分析
基于FFT对信号谐波检测
FFT去噪法的流程是:信号进行傅里叶变换;采用低通滤波器滤除噪声频率成分;对滤波后的信号进行傅里叶逆变换得到去噪后的信号。如图1、2所示,可以看出:对整数次谐波的检测,FFT算法可以精确分析;对于非整数次谐波的检测,仍存在频谱泄漏和栅栏现象。
基于FFT和小波变换对信号的检测
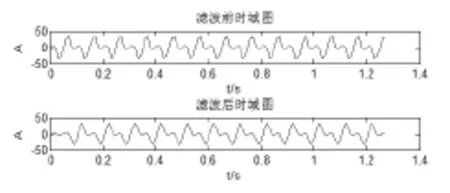
图1 滤波前后时域图

图2 滤波前后频域图

图3 基于FFT和小波变化对s信号的检测
如图3所示,d1是采集的信号,里面含有整数次谐波和非整数次谐波等;d2是含有噪声的信号;d3经小波变换的信号;d4是基于FFT和小波变换的检测的信号。从仿真结果可以看出:小波变换可以除去信号中的非稳态谐波、突变点、间断点等细节分量,然后经FFT变换得出稳态分量,采用FFT和小波变换结合的方法能更好地得出含噪信号的谐波信号,并且实用性更强。
本文介绍了基于FFT和小波变换阈值去噪的谐波检测方法,通过Matlab仿真分析出,采用两种方法相结合的方式去噪效果更明显,谐波检测的精度更高,对于电力系统谐波信号分析具有很广的应用前景。
(安徽理工大学)
