多边形裁剪算法实现与改进
2016-08-19王海涛卫文学
王海涛++卫文学

摘要:计算机图形学是研究基于物理定律、经验方法以及认知原理,使用各种数学算法处理二维或三维图形数据,生成可视数据表现的科学,它是计算机科学的一个分支领域与应用方向。往往在使用计算机处理图像时,占用计算机内部存储空间往往比较大。为了提高效率,计算机往往采用裁剪的方式将图片所需的部分显示,这其中多边形裁剪是重要的一种算法,该文将简述多边形裁剪算法的实现与改进。
关键词:计算机图形学;多边形裁剪;算法;改进
中图分类号:TP301 文献标识码:A 文章编号:1009-3044(2016)20-0185-02
Abstract: Computer graphics is a kind of scientific research based on physical laws, empirical methods and cognitive principles, using various mathematical algorithms to deal with two-dimensional or three-dimensional graphics data, to generate visual data representation of the science. It is a branch of computer science and its application. Often in the use of computer image processing, the occupation of computer storage space is often relatively large. In order to improve the efficiency, the computer is often used to cut out the part of the image, which is an important part of the algorithm, the paper will summarize the implementation and improvement of polygon clipping algorithm.
Keywords: computer graphics; Polygon clipping; algorithm; improvement
1引言
随着计算机的广泛应用以及计算机技术不断地发展,作为计算机领域重要分支的可视化技术近年来也得到了长足的发展。在国外,可视化技术已经较为成熟可以应用于多个领域,比如教学领域,商业领域等。在国内,可视化技术的研究还不太成熟,但是可视化技术已经得到了长远的发展。可视化技术在现阶段拥有较为广阔的发展空间。可视化技术主要分成两类:二维平面图像和三维立体图像。该文在研究可视化技术的基础上,对二维图像裁剪算法进行讨论和优化,生成相应的结果。
要指出最新研究对这个问题存在的不足,以及改进的思路。
2多边形裁剪算法描述
使用计算机处理图形时,往往占用较大的存储空间,而当真正使用或显示的一般是图形的一部分。所以我们就需要将使用到的部分图形显示出来,将其他部分排除在外,这样不仅大大节省了内存开支并且提高了使用和显示效率。这样的选择过程称为裁剪。最直接的裁剪方式是把图形进行扫描后转化为点的集合,最后在判断各点是否在所需部分之内。但那样太费时。所以一般采用的方法是先进行裁剪再进行扫描和转化。
裁剪的算法主要包括线段裁剪算法,多边形裁剪算法,字符裁剪算法等。[1]该文主要围绕多边形裁剪算法进行研究。
多边形可以比作是线段的集合,多边形的裁剪可以相应的转化成每条线段的裁剪。当一个封闭的多边形作为线段的集合进行裁剪时,原来封闭的主多边形转化成一条条由裁剪后的线段及裁剪多边形的部分边界线段构成的边的集合。[2]多边形裁剪算法主要包括Sutherland -Hodgman算法和Weiler-Atherton算法等,其中S-H算法核心思想是通过对多边形某一边的裁剪,来完成对整体的裁剪,简而言之就是每次将主多边形的边与裁剪完的边进行对比,然后输出一个或两个顶点或不输出。这一算法适用于对凸、凹任意主多边形进行裁剪,裁剪多边形为凸多边形。算法输出的结果是一个多边形的顶点序列,所有顶点均位于裁剪多边形的可见侧。由于主多边形的每一条边与裁剪多边形的每一条边分别进行比较,因此需要考虑每条边与每个裁剪边的相对位置关系。此算法还要考虑如何判别交点位于裁剪边的哪一侧以及如何求裁剪边与主多边形线段的交点。W-A算法首先是将主多变形与裁剪多边形比较,标记下二者的交点,然后处理不相交的多边形边界,通过建表分别记录位于裁剪多边形内部和外部的边界。同理建表分别记录主多边形进入裁剪多边形内部的交点和离开内部的交点。最后再从进点表中依次取出一个交点,若该交点为空则结束。比较多边形顶点表直到发现一个交点,将这一段主多边形顶点表复制到内表中。再根据交点位置,找到裁剪多边形顶点表相应位置,跟踪裁剪多顶点表, 直到下一个交点为止,将这一段裁剪多边形顶点表复制到内表中, 再从头开始直到结束,则获得裁剪后的新多边形。[3]
3 S-H算法应用
下面用一个示例演示一下S-H算法的实现。设多边形由如下顶点D1,D2,D3,D4,D5构成,主多边形与裁剪多边形如图1所示。
用程序实现算法,主要程序段描述:
裁剪后的多边形如图2所示。
4 实现对S-H算法的改进
S-H算法是一种较为方便实用的方法,但该算法也存在一些缺点和不足,比如对多边形进行裁剪后,会出现一些不属于裁剪多边形的边。一种方法是将主多边形分成更多的凸多边形,然后依次处理各个凸多边形,然而这样会使得效率降低。另一种方法是在Sutherland-Hodgman算法基础上进行优化,查找顶点表,然后将表中的顶点各个连接起来也比较麻烦。基于上述问题,本文提出了一种算法。此算法的思想为:用最直接的直线段的裁剪算法即依次对多边形的每条边进行裁剪。然后处理主多边形与裁剪多边形的交点,如果该点是裁剪后可见部分的起始点,记为入点,如果该点是可见部分的终止点,记为出点。然后对主多边形的个边顺序逐个裁剪,得到非封闭多边形。显然得到的交点中入点与出点的个数应该相等,且入点与出点沿多边形方向相同的排列,要使裁剪后的多边形封闭,只需要把所有出点与入点进行连接。入点与出点的位置与该多边形边界的关系主要有如下几种:
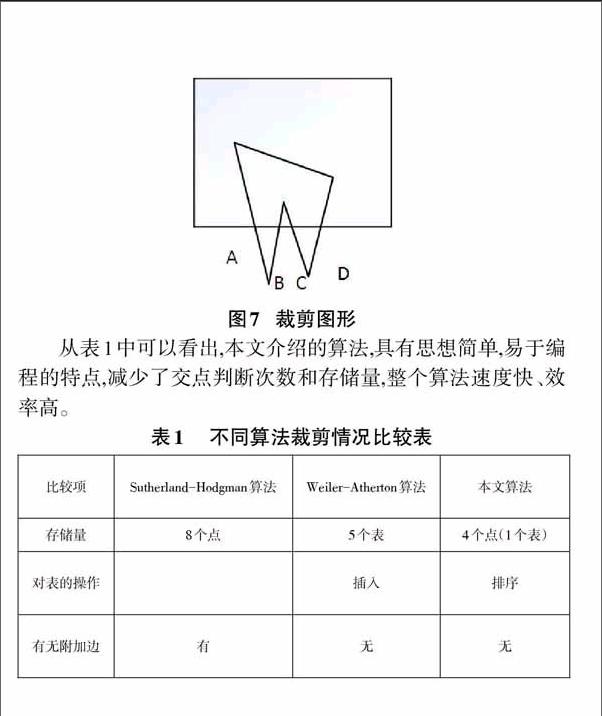
以图7为例将该算法与常规算法进行比较。
从表1中可以看出,本文介绍的算法,具有思想简单,易于编程的特点,减少了交点判断次数和存储量,整个算法速度快、效率高。
5 总结
计算机图形学所包含的算法有很多,本文所研究的裁剪算法是计算机图形学中比较基础的算法,是其他诸多重要问题的基础。该文简单阐述了国内外计算机图形学的发展情况,接着对基本的裁剪算法Sutherland-Hodgman算法和Weiler-Atherton算法进行了简单的介绍,并且通过一个例子描述了Sutherland-Hodgman算法的具体应用,又分析了一下S-H算法的不足。基于上述问题在S-H算法的基础上加以优化和改进,提出了一种更为方便快捷的算法。减少了交点判断的次数和存储量,在应用中效率更高。
参考文献:
[1] 孙家广,胡事民.计算机图形学基础教程[M]. 2版.北京:清华大学出版社,2009.
[2] 常明,朱林.计算机图形学[M]. 2版.华中科技大学出版社,2001.
[3] 付迎春,袁修孝.一种有效的任意多边形裁剪算法[J] .计算机工程,2006(7).
[4] 谭浩强.C程序设计[M]. 2版.北京:清华大学出版社,1999.
[5] 夏德麟,汪应风.多边形裁剪的一种新的方法[J].计算机应用软件,1991(1):60-64.
