论经典命题逻辑矢列演算的保持高度收缩定理
2016-08-19余军成和宝珍
余军成,和宝珍
论经典命题逻辑矢列演算的保持高度收缩定理
余军成1,和宝珍2
(1.贵州工程应用技术学院逻辑与文化研究中心,贵州毕节551700;2.晋中师范高等专科学校政史系,山西晋中030600)
在《结构证明论》中,给出保持高度收缩定理在经典命题逻辑矢列演算中的一个详细而完整的证明过程,得出保持高度收缩的推论并证明了该推论,指出保持高度收缩推论在证明切割规则的可容许性定理上有减少推导步骤的作用。
经典命题逻辑矢列演算;保持高度收缩定理;保持高度收缩推论;收缩规则
1 引言
矢列演算(sequent calculus),是关于结论及其所依赖的假设之间的可推导关系的一种形式理论。[1]它在自动化证明搜索系统(systems of automatic proof search)、逻辑编程(logic programming),尤其是计算机科学、语言学、哲学中应用广泛。
经典命题逻辑矢列演算(内格里(Sara Negri)、柏拉图(Jan von Plato)将系统简称“G3cp”)的收缩规则(contraction rules)源自根岑(Gerhard Gentzen)于1935年在经典谓词逻辑演算(根岑简称“LK”)中首次提出的结构推理图模式之一[2]——收缩(contraction)[3]296。在LK中,收缩推理图模式为:

它在LK-推导以及“主要句子”(the Hauptsatz)及其推论的证明等方面有重要作用。[3]297-302
内格里和柏拉图在G3cp中给出收缩规则是可容许的(admissible)定理及部分证明过程。[4]53-54在此基础上,我们给出保持高度收缩定理一个详细而完整的证明过程,根据该证明得出保持高度收缩的推论并证明了该推论,指出保持高度收缩推论在证明切割规则的可容许性定理上有减少推导步骤的作用。
2 G3cp系统
经典命题逻辑的语言L定义如下:
逻辑公理:
逻辑规则:
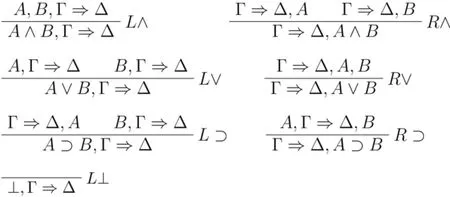
定义1:G3cp系统中一个推导或者是一个逻辑公理,或者是的一个实例(结论),或者是一个逻辑规则应用到包含它的前提的推导。G3cp系统中一个推导的高度是连续应用逻辑规则的最大数目,其中逻辑公理和的推导高度为0。①
3 保持高度收缩定理
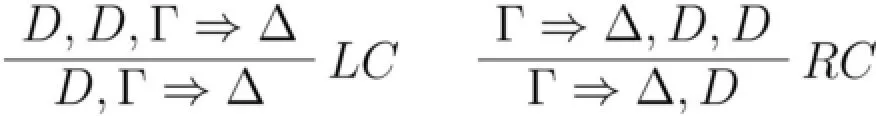
在LK中,收缩推理图模式是结构推理图的基本模式之一。然而,在G3cp中,没有结构规则,和不是G3cp的基本规则,而是导出规则,因此,我们需要证明收缩规则的可容许性,即保持高度收缩定理(the theorem of height-preserving contraction,简称“Ctr-hp”)。③该定理是切割规则(the rule of cut)的可容许性定理证明的前提条件;在探讨矢列演算与自然演绎(natural deduction)的关系等方面有重要作用。

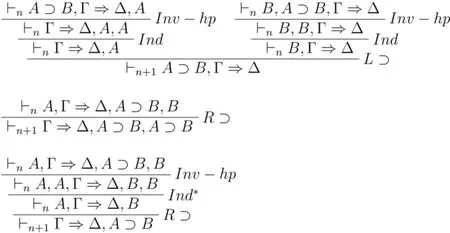
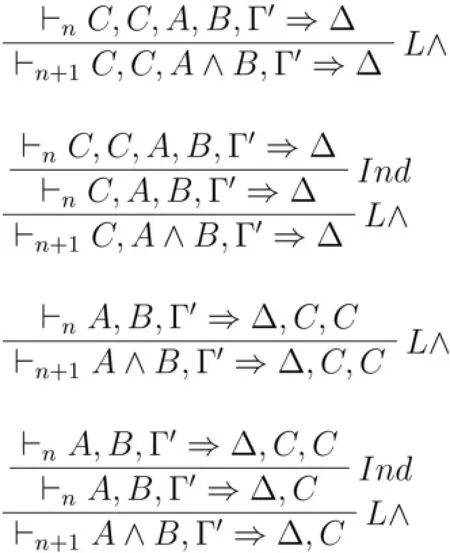



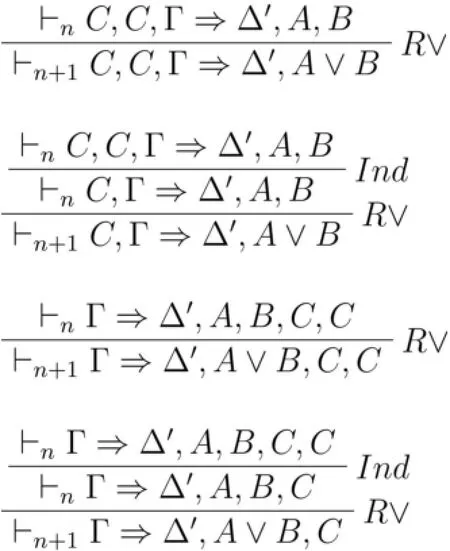
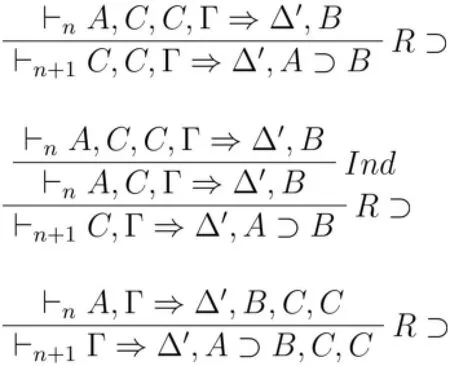
证毕。
4保持高度收缩的推论
推论3(保持高度收缩的推论⑤(the corollary of height-preserving contraction,简称“Ctr-hp*”):对于任意的推导高度、公式和以及多重集合和而言,如果,那么。
在G3cp中,我们发现利用Ctr-hp*有助于减少切割规则可容许性定理证明过程的推导步骤。因为,由“”,无论是先根据LC-hp再根据RC-hp,还是先根据RC-hp再根据LC-hp,得出结论“”的推导步骤需要两步才行;然而,由“”,根据Ctr-hp*,得出结论“”的推导步骤仅仅需要一步就可以了。
5结论
在经典命题逻辑矢列演算中的保持高度收缩定理,我们与内格里和柏拉图的不同之处在于:一是给出保持高度收缩定理一个详细而完整的证明过程;二是根据保持高度收缩定理,得出保持高度收缩的推论并证明了该推论;三是指出保持高度收缩推论在证明切割规则的可容许性定理上有减少推导步骤的作用。
注释:
①本文中加粗的“定义”、“定理”和“推论”采用顺序表示法,特此说明。
②就收缩规则自身而言,LK的收缩规则与G3cp的收缩规则唯一区别在于:在前者中放置的是以逗号分隔的任意公式序列(可能是空序列);在后者中,和是有穷的甚至可能为空的公式的多重集合。
⑤由G3cp扩张到经典谓词逻辑矢列演算系统,该推论显然也是成立的。
[1]Sara Negri&Jan von Plato.Proof Analysis:A Contribution to Hilbert’s Last Problem[M].Cambridge:Cambridge University Press,2011:85.
[2]Szabo.M.E.Collected Papers of Gerhard Gentzen[M].Amsterdam:North-Holland Publishing Company,1996:Bibliography.
[3]Gerhard Gentzen.Investigations into Logical Deduction[J].American Philosophical Quarterly,1964(1).
[4]Sara Negri&Jan von Plato,Structural Proof Theory[M].Cambridge:Cambridge University Press,2008.
[5]Curry,H.B.Foundations of Mathematical Logic[M].New York:Dover Publications Inc.,1977:173.
On the Theorem of Height-preserving Contraction in Sequence Calculus of Classical Propositional Logic inStructural Proof Theory
YU Jun-cheng1,HE Bao-zhen2
(1.Center for Logic and Culture,Guizhou University of Engineering Science,Bijie,Guizhou551700,China;2.Department of Politics and History,Jinzhong Teachers College,Jinzhong,Shanxi030600,China)
InStructural Proof Theory,this paper gives a detailed and complete proof process of the theorem of height-preserving contraction in the sequence calculus of classical propositional logic,obtains the corollary of height-preserving contraction and proofs this corollary,points out that the corollary of height-preserving contraction on the proof of admissible theorem of cut has the function of reducing the derivation steps.
Sequence calculus of Classical Propositional Logic;Theorem of Height-preserving Contraction;Corollary of Height-preserving Contraction;Contraction Rules
B81
A
2096-0239(2016)03-0059-07
(责编:彭麟淋责校:明茂修)
2016-01-15
中央高校基本科研业务费专项资金一般项目“达米特直觉主义逻辑思想演绎研究”,项目编号:SWU1609140;国家哲学社会科学基金重点项目“意识、表征与行动——人类认知的结构与运作机制研究”,项目编号:12AZD073。
余军成(1980-),男,重庆忠县人,贵州工程应用技术学院逻辑与文化研究中心副教授,西南大学博士研究生。研究方向:证明论与哲学逻辑。和宝珍(1980-),女,山西文水人,晋中师范高等专科学校讲师,硕士。研究方向:逻辑学。
