含裂隙岩石的受压破坏机理研究*

唐红梅　张金浩　陈洪凯

(重庆交通大学岩土工程研究所　重庆　400074)



含裂隙岩石的受压破坏机理研究*

唐红梅张金浩陈洪凯

(重庆交通大学岩土工程研究所重庆400074)

含裂隙结构面岩体在加载过程中的裂纹扩张和强度对研究岩体的变形破坏机理具有重要意义。用砂浆裂隙试件模拟含裂隙岩石进行单轴压缩实验，获得了3种倾角(45°、60°、75°)和3种裂隙长度(45mm、60mm、75mm)的9种组合工况的裂隙扩展角度和初裂强度，并分析了9种工况下的受压破坏机理。 实验结果表明：当裂隙长度相同时，初裂强度随倾角的增加而增加，且倾角由60°增加到75°，初裂强度增加得更快； 当裂隙倾角一定时，初裂强度随裂隙长度的增加而降低。应用最大周向正应力理论分析了含裂隙试件的受压破坏机理，获得了裂隙扩展角理论表达式； 通过比较可知：裂隙扩展角的实测值和理论值基本吻合。

实验研究裂隙岩石裂隙扩展角初裂强度破坏机理

0　引　言

在矿山开采和隧道开挖过程中，经常会遇到含裂隙岩石对工程造成威胁，如：渗水、塌方和破坏等工程问题。如果预先了解含裂隙岩石的工程性质和破坏机理，及时做好预防破坏的措施，就会达到很好的处理效果，否则将给人们的人生财产带来极大的损失。目前针对实际裂隙岩石破坏特性的研究主要借助于室内模型实验，李云鹏等(1955)根据断裂力学理论及节理岩体的等效连续模型，探讨了岩体裂隙扩展过程的数值模拟方法。杨圣奇(2013)对断续三裂隙试样进行单轴压缩实验，探讨了岩桥倾角对断续三裂隙砂岩强度破坏和裂纹扩展特征的影响。蒲成志等(2010)对含1条水平裂隙的类岩石试件进行加载实验，结合数值分析结果，探索单压条件下类岩石材料断裂破坏机制。王国艳等(2011)采用岩石破裂过程RFPA数值分析系统，研究了特定应力条件下裂隙长度、无偏置双裂隙的水平间距和竖直间距对裂隙演化的影响。郭保华等(2012)分析了循环加载下岩石裂隙法向闭合机制，通过对粗晶及细晶大理岩裂隙的法向循环加载实验和拟合分析，建立了岩石裂隙法向闭合本构关系。刘昌军等(2012)采用二维无单元法求解有自由面的裂隙岩体渗流问题，并推导了渗流场的基本方程和积分格式。郑刚(2004)利用三轴应力渗透仪分别对煤矿底板的硬岩和软岩进行三轴应力渗透实验，分析了两种岩石的阻水能力及岩体裂隙突水的机理。肖桃李等(2012)以常规三轴压缩实验为手段，研究单裂隙试样的破坏特性。路亚妮等(2014)通过三轴压缩实验，对预制张开裂隙岩样在不同围压下裂隙参数对岩样的强度和变形破坏特征的影响规律进行了研究，并基于冻融循环实验对裂隙岩体的冻融损伤劣化模式进行研究，探讨了经历不同冻融循环次数后的裂隙岩样在三轴压缩条件下裂缝的贯通机制。

国外学者Cotterell(1972)发现岩石内部的斜裂纹在压缩荷载作用下，将产生翼形断裂模式，呈现I型张拉机制破坏机理； Rao et al.(1999)认为，在Ⅱ型加载条件下，试件并不导致剪切破坏的出现； Bobet et al.(1998)指出，在压缩荷载作用下，含裂隙岩石材料的破坏特征并没有只有I型的翼形破坏模式，有可能出现剪切型的共面破坏模式。鉴于此，本文立足于前人的研究，用砂浆裂隙试件模拟含裂隙岩石，分析不同裂隙长度、倾角的试件在单轴压缩荷载作用下裂隙的扩展模式和破坏特征，应用最大周向正应力理论分析含裂隙试件的受压破坏机理，将获得的裂隙扩展角的理论值与实验值对比分析，为矿山开采和隧道开挖提供一些理论帮助。

1　实验模型设计

试件采用普通硅酸盐水泥，强度等级为42.5MPa； 水泥、河砂、水的配合比为1︰3︰0.72； 试件尺寸长、宽、高分别为150mm、150mm、150mm。预置裂隙的制作是用铁片(插入前铁片用薄膜包住，并涂抹一层机油，以便试件成型后能顺利拔出)按照设计的角度斜插入振捣好的水泥砂浆试块中，铁片距试件边缘30mm，并且固定薄片等待试块凝结，试件成型后(48h)取出，并养护至规定龄期(28d)进行实验。裂隙的倾角β(裂隙与水平面的夹角)分为45°、60°和75°，裂隙长度L分为45mm、60mm和75mm 3种，共9中实验工况，每种工况运用5个试件进行单轴压缩实验。例如LF45°-45-1试件，LF代表裂隙试件，前两个数字45°代表裂隙倾角β(°)，后面两个数字45代表裂隙长度L(mm)， 1代表试件编号 (图1)。

图1　裂隙试件的立体模型Fig. 1　The three-dimensional model of the specimen fracture

2　单轴压缩实验分析

实验采用中国科学院武汉岩土力学研究所研制的RMT-301多功能电液伺服实验机进行试件的单轴压缩实验 (图2)。采用位移控制，中等位移速率为0.002mm·s-1。压缩过程中，观察裂隙变化状况和记录裂隙扩展角度，用红色信号笔描出裂隙扩展行迹，并用相机拍摄试件从加载到破坏的整个过程的照片。

图2　裂隙试件加载方式照片Fig. 2　Loading picture of the specimen fracture

(1)当裂隙倾角45°时，裂隙长度45mm、60mm、75mm试件的破坏特征(图3)。

图3　裂隙倾角为45°试件的破坏图片Fig. 3　The damage picture of specimen with fissure angle 45°a. LF-45°-45； b. LF-45°-60； c. LF-45°-75

选取具有普遍破坏现象的试件进行分析，从实验现象可以看出：LF45°-45试件在单轴荷载下 (图3a)，预置裂隙扩展主方向(图中裂隙①的方向)大致平行于压应力方向。随着主裂隙①的扩展，应力集中与预置裂隙端部，试件表面出现支裂隙，主要集中于预置裂隙端部垂直方向。最大支裂隙②的扩展角α(裂隙扩展线与预置裂隙延长线的夹角)值为91°，初裂强度σc为4.95MPa(即试件表面出现裂隙时，记录的强度值)，试件的破坏模式呈现出受压力学机理。LF45°-60试件在加载一段时间后 (图3b)，试件出现了拉裂隙①，这是由于预置裂隙受压闭合所导致。随着荷载的增加，预置裂隙受压剪作用增大，会延裂纹延长线开始扩展，最终沿主裂隙③贯穿整个试件。最大支裂隙②的扩展角α值为88.5°，σc为3.48MPa。试件的破坏模式表现出压剪力学机理。F45°-75试件的预置裂隙长度较大 (图3c)。随加载荷载增大一定程度时，预置裂隙会慢慢闭合，试件受压剪作用明显，在预置裂隙尖端会出现一小段剪裂隙，之后进入压应力状态，最终沿主裂隙②贯穿整个试件，最大支裂隙③的扩展角α值为90.5°，σc为1.57MPa。试件呈现出压剪破坏力学机理。

(2)当裂隙倾角60°时，裂隙长度45mm、60mm、75mm试件的破坏特征(图4)。

图4　裂隙倾角为60°试件的破坏图片Fig. 4　The damage picture of specimen with fissure angle 60°a. LF-60°-45； b. LF-60°-60； c. LF-60°-75

从实验现象可以看出：LF60°-45试件裂隙长度比较小，整个试件表现出完整试件的受力模式 (图4a)，主裂隙①的扩展方向大致平行于压应力方向，最大支裂隙②的扩展角α值为82.5°，σc为5.89MPa。试件的破坏模式呈现出受压力学状态。从LF60°-60试件的破坏图片可以看出 (图4b)受压一段后，预置裂隙开始扩展，导致了主裂隙①的出现。随着荷载的增加，试件内部裂隙会慢慢的扩展衍生，导致了支裂隙②的出现，α值为80.5°，σc为4.18MPa。整个试件表现出压剪破坏机理。LF60°-75试件的裂隙长度较大，由于预置裂隙受压闭合导致拉裂纹①的出现 (图4c)。荷载增大一定程度时，预制裂隙慢慢闭合，试件受压剪作用明显，在预制裂隙尖端会出现一小段剪裂隙，之后进入压应力状态，最终沿主裂隙②贯穿整个试件，最大支裂隙③的扩展角α值为81.5°，σc为2.75MPa。试件最终呈现出压剪破坏力学机理。

(3)当裂隙倾角75°时，裂隙长度45mm、60mm、75mm试件的破坏特征(图5)。

图5　裂隙倾角为75°试件的破坏图片Fig. 5　The damage picture of specimen with fissure angle 75°a. LF-75°-45； b. LF-75°-60； c. LF-75°-75

实验结果表明：由于裂隙试件的倾角75°比较大 (图5)，试件的破坏模式与预制裂隙长度(裂隙长度45mm、60mm、75mm)无关，主裂隙①的扩展方向大致平行于压应力方向，次生裂隙的出现不规律，离散性较大，3种试件的破坏模式呈现出受压破坏机理。试件初裂强度分别为7.55MPa、6.02MPa、5.24MPa。

(4)初裂强度分析

根据在单轴压缩作用下所得到的初裂强度和试件的裂隙长度、倾角，绘制初裂强度与裂隙长度、倾角的关系图，分两种情况。

①第1种：裂隙长度相同，初裂强度与初裂隙倾角的关系(图6)，实验结果(表1)。

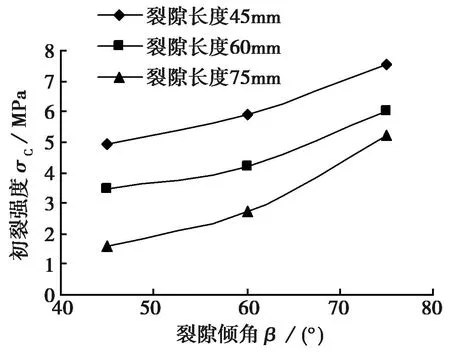
图6　初裂强度与裂隙倾角的关系Fig. 6　The relationship between initial strength and fissure angle

表1　初裂强度实验结果Table1　The experimental results of initial crack strength

裂隙长度/mm裂隙倾角/(°)初裂强度/MPa45454.95605.89757.5560453.48604.18756.0275451.57602.75755.24

实验结果表明 (图6、表1)：对于裂隙长度为45mm、60mm、75mm 3种试件，当裂隙长度相同时，初裂强度随初裂隙倾角的增加而增加。且倾角由60°增加到75°，初裂强度增加得更快。

②第2种：裂隙倾角相同，初裂强度与裂隙长度的关系(图7)，实验结果(表2)。

表2　初裂强度实验结果Table2　The experimental results of initial crack strength

裂隙倾角/(°)裂隙长度/mm初裂强度/MPa45454.95603.48751.5760455.89604.18752.7575457.55606.02755.24

图7　初裂强度与裂隙长度的关系Fig. 7　The relationship between initial strength and fissure size

实验结果表明 (图7、表2)：裂隙倾角为45°、60°、75° 3种试件，当裂隙倾角相同时，初裂强度随裂隙长度的增加而下降。

3　含裂隙试件的受压破坏机理

最大周向正应力理论第一假设：裂纹初始扩展沿着周向正应力σθ达到最大的方向(图8)。

图8　裂隙尖端力学模型Fig. 8　The mechanical model of crack tip

由线弹性断裂力学可知，当几个荷载同时作用弹性体上时，应力可以叠加。对裂隙试件可用叠加原理得到裂纹尖端应力场。

对于I型裂纹尖端应力场(压应力时取负值)：

(1)

对于Ⅱ型裂纹尖端应力场：

(2)

将I型和Ⅱ型裂纹尖端应力场叠加：

(3)

由于在r=0处各应力分量都趋于无穷大，无法得出σθ的极值。因此只能求出距裂纹边缘某一微小距离r=r0的圆周上各点的σθ的值(图8)，并求其极值其所在位置，从而确定裂纹初始扩展角α，裂纹的扩展方向可由式(4)确定：

(4)

将式(3)代入式(4)，得裂纹初始扩展角α的求解方程为：

(5)

在单轴压缩荷载作用下，含有裂纹长度为L，裂纹倾角为β的试件，应力强度因子可由式(6)确定：

(6)

式中，λ1，λ2为考虑有限板两侧由于解除位移约束而使裂纹端部应力强度因子增大的修正系数，采用边界法求得，此处假设λ1=λ2； σ为作用在裂隙试件上的压应力；L为裂隙长度；β为裂隙倾角。

将式(6)代入式(5)得：

(7)

利用式(7)，作出裂隙扩展角α与裂隙倾角β的关系图 (图9)，从图中可以看出，在β∈(30°， 70°)的范围内，曲线呈倒“V”型，在β为45°时达到最大值。将实验所得β代入式(7)，可得到裂隙扩展角的理论值。理论值和实测值结果比较(表1)，通过比较可知：裂隙扩展角的实测值和理论值基本吻合。

表3　裂隙扩展角理论值和实测值Table3　The theoretical and measured values of crack extension angle

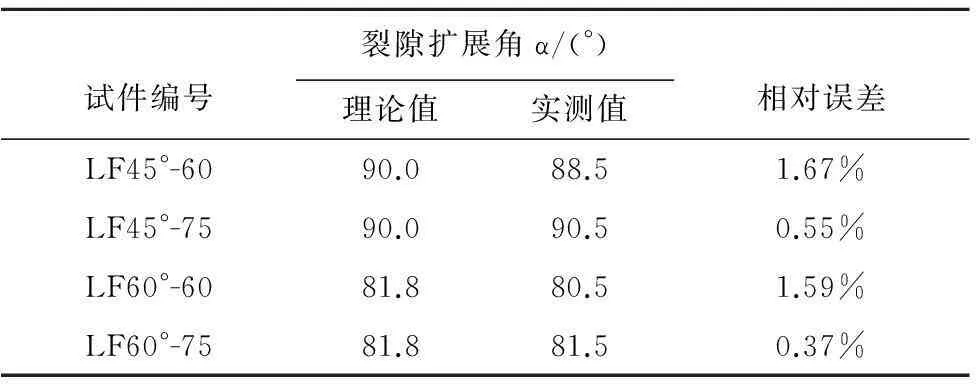
试件编号裂隙扩展角α/(°)相对误差理论值实测值LF45°-6090.088.51.67%LF45°-7590.090.50.55%LF60°-6081.880.51.59%LF60°-7581.881.50.37%

表1只列出压剪破坏机理的试件裂隙扩展角的理论值和实测值的比较； 受压破坏试件为I型裂纹破坏，比较普遍，这里不再列出

图9　裂隙扩展角理论值和实测值对比图Fig. 9　The comparison chart on theoretical and measured values of crack extension angle

4　结　论

(1)通过单轴压缩实验，获得了3种倾角(45°、60°、75°)和3种裂隙长度(45mm、60mm、75mm)的9种组合工况的裂隙扩展角度和初裂强度。

(2)分析了9种工况下的受压破坏机理。实验结果表明：在裂隙倾角为45°时，试件的破坏模式随着裂隙长度的不同而不同。裂隙长度为45mm时，试件受压破坏； 裂隙长度为60mm和75mm时，试件受压剪破坏机理。在裂隙倾角为60°时，随着裂隙长度的不同，试件的破坏模式也不相同。裂隙长度为45mm时，试件受压破坏； 裂隙长度为60mm和75mm时，试件受压剪破坏机理。由于裂隙试件的倾角75°比较大，试件的破坏模式与预制裂隙长度无关，裂隙长度45mm、60mm、75mm试件的破坏模式相同，呈现出受压破坏机理。

(3)根据所得到的初裂强度，分析了9种工况下，初裂强度与裂隙长度、倾角的关系。实验结果表明：当裂缝长度一定时，初裂强度随裂隙倾角的增加而增加。当裂隙倾角一定时，当初裂强度随裂隙倾角的增加而下降。

(4)应用最大周向正应力理论分析了含裂隙试件的受压破坏机理，获得了裂隙扩展角理论表达式，通过比较可知：裂隙扩展角的实测值和理论值基本吻合。

Bobet A，Einstein H H. 1998. Fracture coalescence in rock-type materia1s under uniaxial and biaxial compression[J]. International Journal of Rock Mechanis and Mining Sciences，35(7)： 863～888．

Lajtai E Z. 1974. Brittle fracture in compression[J]. International Journal of Fracture，10(4)： 525～536．

Guo B H，Li X J，Su C D. 2012. Experimental study of constitutive relation for rock fracture under normal cyclic loading[J]. Chine Journal of Rock Mechanics and Engineering， 31(S1)： 2973～2980．

Liu C J，Ding L Q，Ning B H，et al. 2012. Meshless simulation of seepage field and seepage characteristics for fractured rock[J]. Journal of Engineering Geology，20(4)： 570～575．

Lu Y N，Li X P，Wu X H. 2014. Fracture coalescence mechanism of single flaw rock specimen due to freeze-thaw under triaxial compression[J]. Rock and Soil Mechanics，35(6)： 1579～1584．

Li Y P，Wang Z Y. 1995. Numerical simulation of the crack extension process in rock masses[J]. Journal of Engineering Geology，3(4)： 48～53．

Pu C Z，Cao P，Zhao Y L，et al. 2010. Numerical analysis and strength experiment of rock-like materials with multi-fissures under uniaxial compression[J]. Rock and Soil Mechanics，31(11)： 3661～3666．

Rao Q，Stillborg B，Sun Z Q，et al. 1999. Mode II fracture toughness testing of rock[C]. Paris： Int Congress on Rock Mechanics.

Wang G Y，Yu G M，Song C W. 2011. Influence of initial crack geometrical properties on rock crack propagation[J]. Journal of Liaoning Technical University(Natural Science)，30(5)： 681～684．

Xiao T L，Li X P，Guo Y H. 2012. Experimental study of failure characteristic of single jointed rock mass under triaxial compression tests[J]. Rock and Soil Mechanics，33(11)： 3251～3256．

Yang S Q. 2013. Study of strength failure and crack coalescence behavior of sandstone containing three pre-existing fissures[J]. Rock and Soil Mechanics，34(1)： 31～39．

Zhang G. 2004. Experimental study on the permeability regularities of rock cracks under triaxial compression[J]. Journal of Engineering Geology，12(1)： 30～33．

郭保华，李小军，苏承东. 2012. 岩石裂隙法向循环加载本构关系试验研究[J]. 岩石力学与工程学报，31(增1)： 2973～2980．

刘昌军，丁留谦，宁保辉，等. 2012. 裂隙岩体渗流场的无单元法模拟及渗流特性研究[J]. 工程地质学报，20(4)： 570～575．

路亚妮，李新平，吴兴宏. 2014. 三轴压缩条件下冻融单裂隙岩样裂缝贯通机制[J]. 岩土力学，35(6)： 1579～1584．

李云鹏，王芝银. 1995. 岩体裂隙扩展过程的数值模拟[J]. 工程地质学报，3(4)： 48～53．

蒲成志，曹平，赵延林，等. 2010. 单轴压缩下多裂隙类岩石材料强度实验与数值分析[J]. 岩土力学，31(11)： 3661～3666．

王国艳，于广明，宋传旺. 2011. 初始裂隙几何要素对岩石裂隙扩展演化的影响[J]. 辽宁工程技术大学学报(自然科学版)，30(5)： 681～684．

肖桃李，李新平，郭运华. 2012. 三轴压缩条件下单裂隙岩石的破坏特征研究[J]. 岩土力学，33(11)： 3251～3256．

杨圣奇. 2013. 断续三裂隙砂岩强度破坏和裂纹扩展特征研究[J]. 岩土力学，34(1)： 31～39．

郑刚. 2004. 岩体裂隙三轴应力渗流规律的实验研究[J]. 工程地质学报，12(1)： 30～33．

LABORATORY TESTS ON FAILURE MECHANISM OF FRACTURED ROCK UNDER COMPRESSION

TANG HongmeiZHANG JinhaoCHEN Hongkai

(Institute of Geotechnical Engineering， Chongqing Jiaotong University， Chongqing400074)

The crack propagation and strength of fissured rocks under applying loads are significant for the study of rock deformation mechanism. Mortar fractured specimens have been simulated as fissured rock in the uniaxial compression experiment. Different crack length， the initial propagation angle of specimens and initial crack strength have been obtained by setting 9 experimental conditions. They have 3angles of 45°， 60° and 75° and 3 crack length of 45mm， 60mm and 75mm. The compression failure mechanism is also analyzed. The results show the following. When the crack length is the same， the initial crack strength is increased by the increase of angles. When the angle is increased from 60°to 75°，the initial crack strength is increased faster. When the crack angle stays at a certain level， the initial crack strength is decreased by the increase of the crack length. By employing the theory of maximum circumferential stress， the failure mechanism of fractured specimens under compression is interpreted. Theoretical expression of crack propagation angle is acquired. By comparison， it is found that the measured and theoretical values of crack propagation angle are in good agreement．

Experimental study， Fractured rock， Crack propagation angle， Initial crack strength， Failure mechanism

10.13544/j.cnki.jeg.2016.03.004

2015-04-18;

2015-11-09.

国家自然科学基金(11272185， 51378521)，重庆市重点自然基金项目(cstc2013jjB30001)资助.

唐红梅(1986-)，女，博士，研究员，硕士生导师，主要从事地质灾害减灾理论与减灾技术的研究. Email: hmtang6778@sina.com

TU458+.3，O346.1

A