织机机架结构减振技术研究
2016-08-18邱海飞
邱 海 飞
(西京学院 机械工程学院,西安 710123)
研究与技术
织机机架结构减振技术研究
邱 海 飞
(西京学院 机械工程学院,西安 710123)
针对以往的织机减振措施,将先进的数字化技术应用于机架动态性能改进。以某型机架为研究实例,综合运用有限单元法、参数化建模及动态优化技术等现代设计手段,建立机架结构动力学优化数学模型,以实现机架组件的结构改进与动态性能提升,有效增强了机架结构抗振性能。通过响应面分析和局部灵敏度分析,为实际机架减振实验指明方向,即:上撑档与前下撑档位置对机架抗振性能敏感度较大,可重点予以控制与改造。为织机系统减振和机架结构改进提供了重要技术参考。
机架;减振;织机;优化;有限元;响应面;灵敏度
近年来,随着纺织机械装备的高速、高精度化发展,新型织机的车速已经高达2 000 r/min。生产实践表明,良好的机架结构对于织机的稳定运行至关重要,它不仅有利于提高织物表面质量和织造效率,而且能够有效延长织机的使用寿命[1]。在当前推动纺织工业振兴的大环境下,中国纺织企业都在积极地进行产业升级,而且在不断淘汰落后产能和技术装备。这种背景下,为了适应新型织机的发展要求,有必要提高织机系统的稳定性和生产效率,同时需要探索更为有效的机架结构及其减振技术,以促进纺织企业的转型与升级。
随着现代CAD/CAE技术的日益成熟,数字化技术为织机机架的设计提供了新的手段。通过在计算机平台上综合应用各种现代设计方法,如参数化建模、动态分析、有限单元法及结构优化算法等[2],不仅保证了机架组件的标准化与完整性,而且可以在数字化运行模式下方便、快捷地实现机架性能优化,避免了机架结构的二次改造和再装配,有利于机架减振设计和织机系统集成化发展。
1 机架减振措施
机架是织机的支撑基础和主要承载部件。在织造生产过程中,织机各运动机构产生的动态冲击载荷经由机架向机体各部位传播,由此形成的激振会引发织机系统产生不同幅度的振动和噪声[1]。例如,打纬主轴曲拐旋转时形成的偏心力、筘座和钢筘产生的惯性打纬力及综框往复运动形成的周期性冲击载荷等,均会直接或间接地作用于机架[2],从而弱化机架结构稳定性,使其在织造过程中发生振动,影响织机的稳定运行和正常生产。
以往对于织机机架的减振措施主要有:对曲轴添加配重或减振装置,采用抗振性强的材质制成墙板或向墙板内部填充减振材料(如铸矿石),在机架基础部位安装减振装置或消振器等。例如黄富贵等[3]将豆包消振器应用于织机机架减振,在较宽频带范围内有效增强了机架结构的抗振性能。织机整机是一个复杂的机电集成系统,其五大机构均安装于机架之上,传统的减振措施多以添加额外减振装置为主,这样不仅增加了机架的承载负担,而且容易造成各运动机构之间产生载荷传递,影响织机系统稳定性。
实际情况下,由于受到机架装配工艺限制,而且难以准确把握减振装置的添加部位,传统的减振措施往往不能获得较为理想的减振效果。此外,减振器属于消耗易损件,且价格较贵,长期在高频强振状态下工作会缩短其使用寿命[4],不利于纺织企业生产节约、降低成本,这种情况下就需要创新思路,探索和尝试新的机架结构减振技术。
2 机架数字化模型
织机机架一般由墙板、胸梁、后梁及撑档构成[5],如图1所示为某型织机机架结构的数字化CAD模型,其中左、右墙板呈对称分布,中间由矩形或圆形截面的空心梁件连接。以机架各零部件的几何点(图1中矩形标识)为参考,分析和建立机架结构数字化模型,并通过几何点坐标来控制各零部件的位置分布,为机架参数化设计与结构优化奠定基础。
基于参数化驱动的数字化模型大大提高了机架设计的可塑性。以此模型为平台,可以无限次对机架进行结构优化与深入研究,避免了实际物理机架的改造实验,不仅有效提高了机架设计的效率和质量,而且减少了实验次数和成本,为织机机架性能研究与改进提供了有力支持。

1.左墙板,2.右墙板,3.胸梁,4.后梁,5.上撑档, 6.下撑档(机前),7.下撑档(机后)图1 机架结构数字化模型Fig.1 Digital model of frame structure
3 动态计算与分析
3.1有限元模型
织机机架为连续实体结构。根据有限单元法和振动力学理论,可将具有无限自由度的实体近似等效为有限自由度的离散结构[6-7]。采用Solid186单元对机架进行结构离散,如图2所示。Solid186是高阶的三维六面体20节点实体单元,每个节点有3个自由度,即沿节点坐标系X、Y、Z方向的平动[8-9]。此外,该单元具有二次位移,可适用于不规则的网格模型,同时具有塑性、超弹性、蠕变、应力刚化、大变形和大应变等功能。
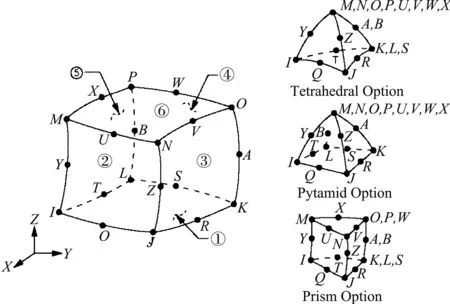
图2 Solid186单元结构Fig.2 Structure of element Solid186
为了提高计算效率和网格质量,对机架结构进行简化处理,忽略紧固件联接及墙板上一些无关紧要的结构特征[5]。根据实际工况,在左、右墙板底部设置固定约束。机架有限元网格模型如图3所示,共包括8 124个单元和57 183个节点。选用吸振性强的灰铸铁作为墙板材质,其余连接部件材质均采用结构钢[10],材料性能参数见表1。

图3 机架有限元模型Fig.3 Finite element model of the frame表1 材料属性Tab.1 Material property

材质密度/(kg·m-3)弹性模量/GPa泊松比灰铸铁72001100.28结构钢78502000.33
3.2模态频率与振型
根据振动理论,低阶模态对结构的动力学特性最为敏感[8],故在此只关心机架前两阶模态频率和振型,如图4所示。由图4可知,机架在第一阶模态频率f1(20.079 Hz)下的振动模式主要表现为左右横向摆动,最大变形区域出现在胸梁与墙板连接处;机架第二阶模态频率f2增大到了27.058 Hz,此时机架上部位置发生扭转振动,最大变形出现在后梁、上撑档及其与墙板连接区域。

图4 机架1、2阶模态振型Fig.4 Top 2 moding shape of the frame
由模态分析结果可知,当织机车速频率在20 Hz或27 Hz附近时,机架容易发生剧烈的横向或扭转振动,并有可能在墙板与胸梁、后梁及上撑档连接处出现严重破坏,由此为织机的车速控制与减振设计提供了重要依据。
4 结构优化
4.1优化基本原理
优化设计是建立在近代数学规划论和计算机程序开发基础上的现代设计方法,其基本原理是运用各种优化方法,通过满足一定约束条件下的迭代计算来获得最优化设计方案。织机机架优化设计数学模型如下式所示:
(1)
式中:f(X)为目标函数,gi(X)为状态变量函数,X为设计变量。
在模态分析基础上,采用Response Surface算法对织机机架进行结构优化,搭建如图5所示的机架优化流程,通过有限元计算建立设计空间的响应面/曲线,然后分析获得最优化设计方案。
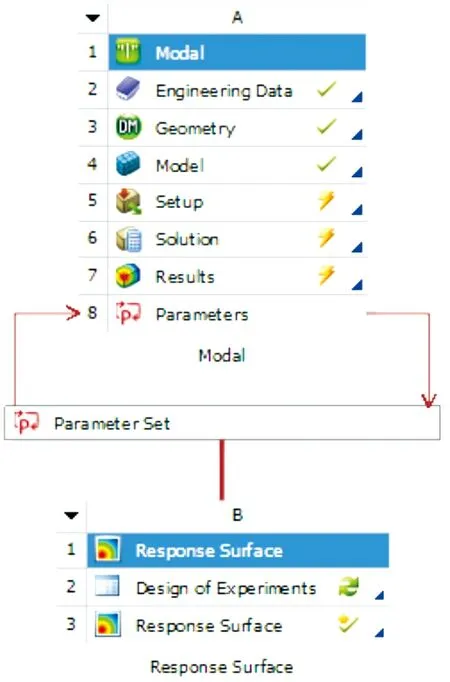
图5 机架优化流程Fig.5 Optimal process of the frame
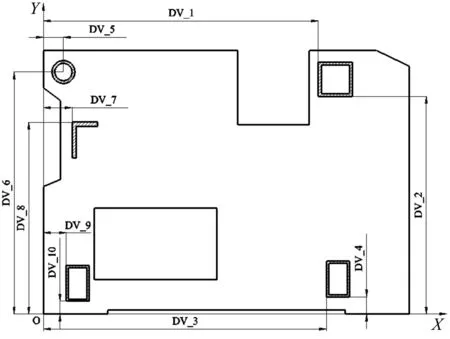
图6 定义设计变量Fig.6 Set design variable
4.2定义设计变量
考虑到机架的抗振性,以提高第一阶模态频率f1为寻优目标。保证机架结构及其组成部件尺寸不变,通过调整胸梁、后梁及撑档在两侧墙板上的安装位置来实现机架动态性能改进。以墙板左下角为坐标原点建立直角坐标系,如图6所示,沿底面水平方向定义X轴,沿左端面垂直方向定义Y轴,各部件初始安装位置以坐标原点为参照。
将机架上各部件的安装位置坐标定义为设计变量。由图6可知,共存在10个设计变量,即DV_1~DV_10,其中DV_1、DV_3、DV_7、DV_9为X方向变量,DV_2、DV_4、DV_6、DV_8、DV_10为Y方向变量,各设计变量的初始值和取值区间如表2所示。

表2 设计变量取值Tab.2 Value of design variable
5 结果分析
5.1频率极值
执行Response Surface优化计算过程,利用Min-Max Search函数统计获得机架前两阶模态频率极值以及与其对应的设计变量值。如表3所示,共有五组机架结构设计方案,其中A为初始频率,B为f1取最小值,C为f2取最小值,D为f1取最大值,E为f2取最大值。
由表3可知,对于方案B和方案C,机架前两阶模态频率均小于优化前的初始频率值,不利于提高机架结构抗振性,故设计机架时尽量不选取这两种方案的设计变量组合。方案D和方案E的前两阶模态频率大小非常接近,而且均高于方案A,说明在这两种设计变量组合方案下皆可实现机架结构优化,但实际当中往往更关心第一阶模态频率f1。比较可知,D方案的f1比E方案高0.47 Hz,因此选D方案为最优化设计方案。

表3 优化前后结果比较Tab.3 Result comparison before and after optimization
计算并提取机架在方案D下的前两阶模态振型,如图7所示。分析可知,优化后的机架振型与图4所示机架振动模式相似,即均表现为一阶横向振动、二阶扭转振动,只是变形区域和振动幅度不同。但是与优化前(方案A)相比,D方案的第一模态频率f1为22.37 Hz,相对A方案增大了2.29 Hz,提高幅度约11.40%,有效增强了机架抗振性,相当于将织机主轴转速提高了近138 r/min,降低了机架振动对织造生产的不利影响,有利于织机高速化发展。

图7 D方案下的机架1、2阶振型Fig.7 Top 2 moding shape of the frame for project D
5.2响应面分析
实际工程设计中,响应面法(Response Surface)主要用于结构的可靠性分析和优化设计[9],其基本原理是利用合理的试验设计(DOE)方法及实验得到相关分析数据,并通过多元二次回归方程来拟合影响因素与响应值之间的函数关系,在此基础上解决多变量问题的优化问题。
织机机架的响应变量为低阶模态频率f1、f2,影响因素为机架各零部件的安装位置坐标,即:DV_1~DV_10,故定义响应函数如式(2)所示。
fi=η(DV_1,DV_2,…,DV_10)
(2)
通过优化计算获得机架结构与模态频率f1、f2之间的3D响应面,如图8所示,其中垂直方向坐标表示模态频率fi,其余两个方向坐标分别表示各零部件在墙板平面上的位置坐标。
3D响应面可直观反映各连接部件位置对机架前两阶模态频率的影响,例如对于机架后下撑档,减小DV_9、增大DV_10可提高f1、f2,如图8(h)(i)所示。

图8 机架结构响应面分析Fig.8 Response surface analysis of frame structure
响应面分析结果为机架结构优化设计和灵敏度分析提供了重要依据。
5.3局部灵敏度
灵敏度分析主要用于定性或定量地评价模型参数误差对模型结果产生的影响,在模型参数化过程和校正过程中具有重要作用[9]。局部灵敏度(Local Sensitivity)分析检验单个参数变化对模型运行结果的影响程度,如图9所示。在各设计变量的变化范围内,总体来看,DV_8对机架前两阶模态频率f1、f2的影响最大,其灵敏度分别为-0.105和-0.102,而DV_7、DV_4的影响程度次之,分别为0.029和0.039,说明上撑档和前下撑档的安装位置会对机架动力学性能产生重要影响。相比之下,DV_1、DV_5及DV_6对f1的影响较小,DV_5、DV_6对f2的影响较小,说明胸梁和后梁位置对机架模态特性影响较小。
局部灵敏度分析为织机机架结构改进和可靠性设计指明了方向。由分析结果可知,对机架进行结构设计时,可重点考虑调节上撑档、前下撑档的安装位置,这样可以快速、有效地实现机架结构优化和性能改进。
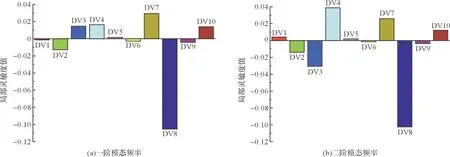
图9 局部灵敏度分析Fig.9 Local sensitivity analysis
6 结 语
现代设计方法为纺织机械装备研发提出了新的思路,革新传统设计模式、降低技术成本和提高产品性能,对于中国纺织工业的振兴与技术升级具有重要现实意义。通过综合运用多种现代设计手段,如有限元方法、参数化设计、动态优化、响应面分析及灵敏度分析等,实现了织机机架的结构改进和动态性能提升,不仅将机架基频提高了约11.40%,同时计算和明确了机架结构局部灵敏度,为机架结构设计和纺织机械装备数字化改造提供了重要技术支持。
[1]吴锋,张升陛.织机机架结构动态特性分析及织机运转状态下的振动分析[J].机械科学与技术,1997,16(3):463-468.
WU Feng, ZHANG Shengbi. Dynamic analysis of loom frame structure and vibration analysis of loom frame under operating condition[J]. Mechanical Science and Technology,1997,16(3):463-468.
[2]薛元,李风强.织机机架振动有限元分析[J].青岛大学学报(工程技术版),1998,13(2):41-45.
XUE Yuan, LI Fengqiang. Finite element analysis of the loom frame work vibration[J]. Journal of Qingdao University Engineering (Technology Edition),1998,13(2):41-45.
[3]黄富贵,吴锋,张升陛.用豆包消振器提高喷气织机机架减振性[J].华侨大学学报(自然科学版),1997,18(4):391-393.
HUANG Fugui, WU Feng, ZHANG Shengbi. Improving the shock-absorption of the frame of a jet loom by applying bean bag damper[J]. Journal of Huaqiao University (Natural Science),1997,18(4):391-393.
[4]余先淮,朱家亮,刘善祥,等.ZA205i型喷气织机减振器的维修[J].棉纺织技术,1999,27(3):54.
YU Xianhuai, ZHU Jialiang, LIU Shanxiang, et al. Maintenance of the shock absorber on ZA205i air-jet loom[J]. Cotton Textile Technology,1999,27(3):54.
[5]李晶,王栋,雒洁,等.织机机架的有限元建模[J].纺织学报,2010,31(9):128-131.
LI Jing, WANG Dong, LUO Jie, et al. Developing model of loom frame based on finite element method[J]. Journal of Textile Research,2010,31(9):128-131.
[6]成大先.机械设计手册单行本(机械振动·机架设计)[M].北京:化学工业出版社,2006:3-28.
CHENG Daxian. Offprint of Mechanical Design Handbook[M]. Beijing: Chemical Industry Press,2006:3-28.
[7]邱海飞,王益轩,刘欣.综框模态频率优化设计[J].机械设计,2012,29(5):35-38.
QIU Haifei, WANG Yixuan, LIU Xin. The optimal design for modal frequency of heald frame[J]. Journal of Machine Design,2012,29(5):35-38.
[8]朱伯芳.有限单元法原理与应用[M].北京:中国水利水电出版社,知识产权出版社,2009:427-453.
ZHU Bofang. Principle and Application of Finite Element Method[M]. Beijing: China WaterPower Press, Intellectual Property Right Press,2009:427-453.
[9]许京荆.ANSYS/Workbench工程实例详解[M].北京:人民邮电出版社,2015:45-67.
XU Jingjing. Explanation of Engineering Example for ANSYS/Workbench[M]. Beijing: Posts and Telecom Press,2015:45-67.
[10]邱海飞,王益轩.双侧四连杆打纬机构动态载荷计算与仿真[J].纺织学报,2014,35(9):144-148.
QIU Haifei, WANG Yixuan. Calculation and simulation of dynamic load for four-bar beating-up mechanism at both-side[J]. Journal of Textile Research,2014,35(9):144-148.
Research of damping technology for the structure of loom frame
QIU Haifei
(College of Mechanical Engineering, Xijing University, Xi’an 710123, China)
In view of traditional vibration mitigation measures for the loom, advanced digital technology is applied to improve its dynamic performance of loom frame. A certain type of frame is used as the research example, and its optimized dynamic mathematical model is set up based on comprehensively applying various modern design methods such as finite element method, parametric modeling and dynamic optimization technique. Then, the structure and dynamics performance of the frame components are improved, and its damping property is also effectively strengthened. Besides, the direction of the frame’s damping experiment is pointed out through response surface analysis and local sensitivity analysis, that is, the upper supporting pin and lower supporting pin in front should be mainly controlled and reformed, because they are very sensitive to frame vibration damping property. In result, some important technical reference is provided for loom damping and frame structure improvement.
frame; vibration damping; loom; optimizing; finite element; response surface; sensitivity
10.3969/j.issn.1001-7003.2016.07.007
2016-01-08;
2016-06-02
陕西省教育厅科研计划项目(15JK2177);西京学院科研基金项目(XJ150216)

TS103.3
A
1001-7003(2016)07-0032-06引用页码: 071107
