基于核主成分分析方法的水面舰艇空中目标威胁评估*

李冬雷,姜礼平

(海军工程大学,湖北武汉　430033)



基于核主成分分析方法的水面舰艇空中目标威胁评估*

李冬雷,姜礼平

(海军工程大学,湖北武汉430033)

对来袭空中目标的威胁进行评估与排序是舰艇对空火力分配的重要一环。根据来袭空中目标的特点,在确定目标指标后进行相应量化,针对来袭目标各指标间非线性的特点，提出使用核主成分分析法对目标信息进行特征提取,随后依据核主成分方差贡献率对威胁目标进行评估与排序。通过仿真算例验证,所得结果较为准确、客观,有效地克服传统方法中主观性较强的问题,并且在对指标数据提取的过程中降低了相关信息维数,降低了计算复杂度,为舰艇防空作战威胁评估提供了新途径。

威胁评估;核主成分分析;舰艇防空作战;空中目标;方差贡献率

随着空中来袭对舰攻击武器的发展,其速度、抗干扰程度及毁伤能力不断提升,对舰艇的威胁程度日渐提高,水面舰艇所面临的防空形势越发严峻。作为火力分配的重要部分,如何实时、准确地对空中来袭目标的攻击意图、威胁程度进行判断,为指挥员做出对空防御决策提供可靠依据成为水面舰艇对空防御威胁评估研究的重点。对于空中来袭目标的评估问题,已有不少研究成果,已知文献中有基于模糊综合评判的方法[1]、神经网络法[2]、灰色关联度方法[3]、TOPSIS方法[4]、D-S证据理论方法、云模型方法等。上述方法各有所长,但均需人为确定目标权重,目标权重指标盲目性和主观性较强,具有依赖先验知识、模糊不确定性强或只是将问题做线性简化而未考虑指标间相互影响等缺陷[5]。主成分分析法在指标权重选取过程中较好地避免了主观因素的干扰,可以较客观地反映目标间的线性关系[6]。然而由于空中来袭目标的各项指标相互间多为非线性关系,主成分方法虽避免了指标权重选取的主观性,但对于非线性指标并不能得到准确的结果。本文就此探讨研究更适合对非线性数据进行处理的核主成分分析方法,用于对来袭空中目标威胁度的评估与排序,取得了较为准确的效果,为舰艇防空作战威胁评估提供了新途径。

1　威胁评估指标量化值的确定

影响空中目标威胁度的因素很多。众多评估因素中,既有定性描述,又有定量描述,且相互间关系复杂,需要将这些因素综合进行考虑。为准确、合理评估空中目标威胁程度,根据专家意见及作战实际,确定了以下六个指标作为评判的依据,并通过各指标的隶属度函数对定性和定量指标进行规范化处理,得到各指标的函数值,设定各指标值的范围为[0,1]。

1)目标距离

目标距离我舰的距离与防御时间成正比,与我舰的威胁程度成反比,目标距离隶属度函数可表示为

(1)

式中，D1=30km;D2=300km;kd=10-2。

2)目标速度

空中目标的飞行速度直接影响舰艇防空火力对其杀伤的概率,飞行速度越快,对我舰的威胁程度越高。通常情况下,目标的飞行速度与威胁程度成正比。目标速度隶属度函数可表示为

y(v)=1-exp(αv)

(2)

式中，v>0,单位为Ma;α=-1.02。

3)目标高度

近年来的局部战争表明,低空突防是有效的攻击形式,来袭目标如敌机和反舰导弹,大多采用降低飞行高度的方式来提高突破我舰对空防御体系使得攻击成功的概率,判断目标高度对舰艇安全至关重要。目标的飞行高度越低,我舰发现距离越短,我舰抗击反应时间越少,越难以拦截。目标高度隶属度函数可表示为

(3)

式中，a=0.05km,kh=2×10-2。

4)目标弦角

目标弦角是以我舰和目标连线为基准与目标运动方向的夹角(设顺时针方向为正)。当目标弦角在[0,90°]区间时,表明空袭目标向舰艇作接近运动时,攻击意图越明显,其威胁会越来越大;当进攻角超出此范围时表示目标远离我舰,其威胁会越来越小。目标弦角越小,目标对我舰威胁越大,当目标弦角接近于0°时,威胁程度最大。选用的目标弦角威胁度隶属函数形式为

y(θ)=exp(-kθθ2),-90°≤θ≤90°

(4)

式中，kθ=3.5×(π/180)2。

5)目标抗干扰能力

空袭目标的电子干扰能力强弱是指在作战中,目标对我舰火控雷达干扰能力越强,其威胁就越大。威胁指标范围是[0,1],可按照等级划分为{无、很弱、弱、较弱、一般、较强、强、很强、非常强},对应的威胁度量化值为{0,0.1,0.3,0.4,0.6,0.7,0.8,0.9,1.0}。

6)目标类型

空袭目标的类型不同,其战术技术性能、攻击能力和电子干扰能力不尽相同,对我舰艇的威胁程度也不同。结合对舰艇构成威胁的常见空中目标类型,对空袭目标类型量化指标为:{弹道反舰导弹、飞航反舰导弹、轰炸机群、战斗机群、轰炸机、歼击机(战斗机)、电子战飞机、预警机、其他飞机},对应的威胁度量化为{1.0,0.9,0.8,0.7,0.6,0.5,0.3,0.2,0.1}。

2　核主成分分析原理

主成分分析的主要思想是以尽可能少的信息损失为原则,构造少数几个不相关的新变量,得到的新变量是原始变量的线性组合[7]。换言之,主成分分析(principal components analysis,PCA)就是通过投影的方法将高维数据空间投影到低维空间,并尽可能地使低维空间数据含有高维空间中原数据的主要特征信息。但由于PCA方法的本质是基于线性代数理论的,因此在处理非线性问题时,会使主成分方法特征提取能力下降,并不能取得良好的效果。随着近年来对支持向量机(SVM)研究的深入,其中的核方法得到了广泛应用[8],由此产生了基于核函数思想的核主成分分析(kernel principal components analysis,KPCA)方法。其主要思想是通过非线性映射将样本空间映射到高维的特征空间中,在映射的特征空间内,使用传统的线性方法进行特征提取,可有效完成对样本空间的非线性特征提取。在映射过程中引入核函数,可以进行隐式空间映射,通过计算样本空间数据之间的内积,便可完成映射。大量实验证明KPCA方法可以较好地解决小样本、非线性、高维数的样本,只要核函数选取合适,便可使得第一项核主成分的贡献率达到90%以上。核主成分分析的原理如图1所示。

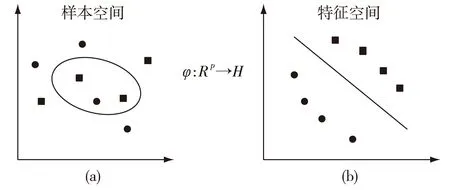
图1　核主成分分析原理图

设样本空间有m个样本点x=(x1,x2,…,xm),xi=(xi1,xi2,…,xip)′是一p维列向量,每个样本有n项指标,并且数据分布是非线性的。首先将处理后的样本数据映射到特征空间H=φ(xi)中,然后在该特征空间中进行主成分分析,最后对所得到的核主成分进行综合评价,得到最终评价系数。

具体步骤为:

步骤1:根据样本数据确定各指标的隶属度函数值,并对数据进行归一化处理,得到m个样本的n项指标,得矩阵X。

步骤2:标准化处理数据

(5)

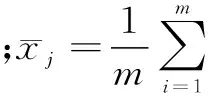
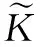
步骤4:给定一个测试点既样本点xi,映射值为φ(xi),计算其在向量αk上的投影值,即第k个核主成分yk。

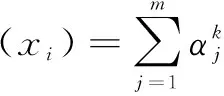
(6)

步骤5:求出第i个样本的评价系数,根据核主成分的方差贡献率进行综合评价,并对评价系数进行排序。第i个样本的系数为

(7)

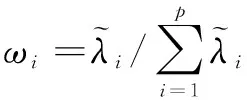
3　仿真算例分析

设在一次演习中,作战信息系统采集到10批空中目标(分别为T1,T2,…,T10),经数据筛选、处理,综合多方多级处理得到来袭目标威胁评估指标如表1所示。各项威胁评估指标经量化处理得到的隶属度如表2所示。

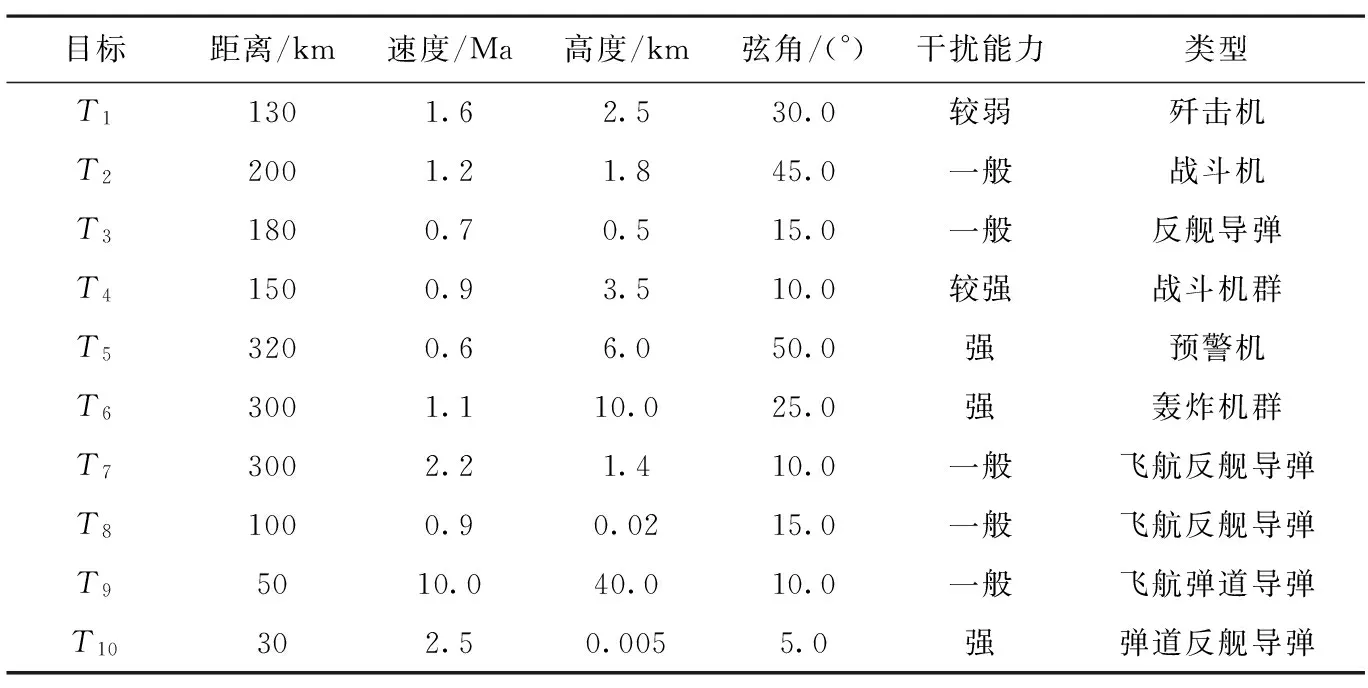
表1　空中威胁目标原始指标数据

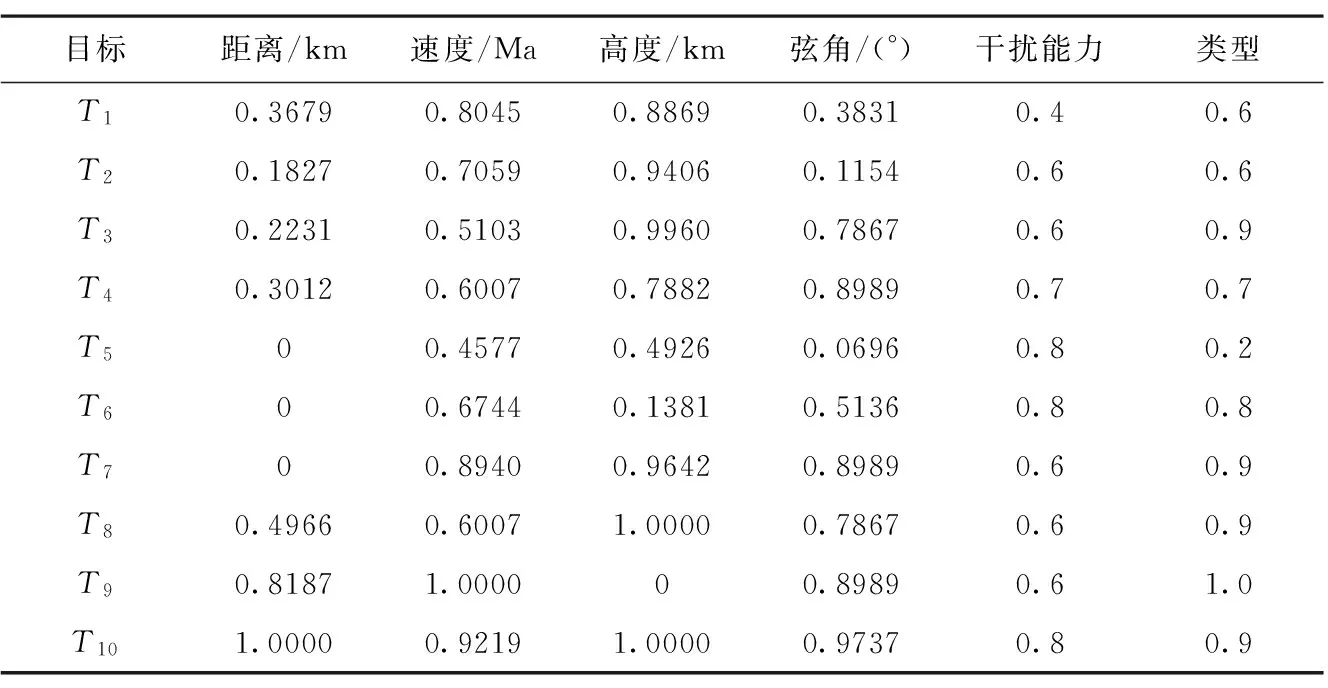
表2　各评估指标量化得到结果

根据上述的KPCA分析方法对空袭目标进行威胁评估,通过Matlab 2014编程计算,选用高斯径向基核函数(RBF),其中选取核函数参数σ=6,规定核主成分的贡献率大于85%。

经计算各成分的贡献率降序为:(0.4056,0.2232,0.1556,0.1097,0.0571,0.0273,0.0136,0.0065,0.0015,0.0000)。累计贡献率:(0.4056,0.6288,0.7844,0.8941,0.9511,0.9784,0.9920,0.9985,1.000,1.000)。由于前四项核矩阵的特征向量贡献率已达到89.41%大于85%,满足要求,随后计算样本点在前四项向量αk上的投影作为第k个核主成分,最后根据式(7)计算各样本的评价系数,得到最终威胁评估排序。

表3　各目标评价系数

从表3中可判断出,目标9威胁最大,目标5威胁最小,最终威胁评估排序结果为9>10>7>8>4>6>1>3>2>5。使用Topsis[4]方法对目标进行威胁排序的结果为9>10>7>8>3>1>4>6>2>5。两种方法均判定目标9为飞航反舰导弹,速度快、干扰强且距离我舰较近,目标5为预警机,虽干扰强、舷角大但对我舰不能造成直接杀伤因此威胁偏小。其中目标4为干扰较强的战斗机群而目标1为干扰较弱大单架歼击机,且目标4舷角更小,故整体威胁更大;目标6为轰炸机群,且干扰能力较单普通的反舰导弹目标1更为强烈,故排序靠前。威胁排序结果整体上与Topsis方法排序一致,证明了本文方法的可行性和有效性。总体来看来袭弹道导弹、反舰导弹目标的威胁偏大,这与近年来反舰导弹技术发展迅猛,毁伤效果更为强烈而日益成为水面舰艇的主要威胁目标的实际符合。算例分析结果表明,通过本文方法计算的结果较为客观、合理,并且符合实际情况,为下一步科学、合理地进行火力分配提供数据支持。

4　结束语

水面舰艇空中来袭目标威胁评估的实质是多属性的综合评估,既将用不同量纲描述目标的指标通转化为无量纲的指标值,然后通过综合这些指标得到目标的整体评价。针对目标指标间的非线性特点,本文通过核主成分方法对目标特征进行提取,通过综合评价得到目标威胁系数及排序,客服主观因素的影响,客观反映了目标的威胁程度。使用核主成分方法虽可降低数据的维数,提取数据关键信息,但同时也损失了原始数据的部分含义,使提取出的核主成分不易理解。在KPCA分析过程中,如何选取合适的核函数及核参数的确定仍较为困难。核参数的选取对实验仿真结果有至关重要的作用,对于核参数的确定,下一步研究可引入更多的训练样本,并使用粒子群优化算法对KPCA的核函数参数进行自动寻优。

[1]Feng L Y, Xue Q, Liu M X. Threat evaluation model of targets based on information entropy and fuzzy optimization theory[C]∥Proc.of the IEEE International Conference on Industrial Engineering and Engineering Management, 2011:1789-1793.

[2]Fu L. Wang Q. Xu J.et al. Target assignment and sorting for multi-target attack in multi-aircraft coordinated based on RBF[C]∥Proc.of the 24th Chinese Control and Decision Conference, 2012:1935-1938.

[3]Li Y X,Wang K Z.Index weight technology in threat evaluation based on improved grey theory[C]∥Proc.of the International Symposium on Intelligent Information Technology Application workshops, 2008:307-310.

[4]Wang B H, Huang J G, Qin X S, et al. Research on FTOPSIS model of threat synthetic evaluation in multi-target tracing system[C]∥Proc. of the IEEE International Conference on Industrial Engineering and Engineering Management, 2007: 35-39.

[5]陈维义,王少蕾,周菲.基于加权核主成分TOPSIS方法的舰艇防空威胁评估[J].海军工程大学学报,2014(1):87-91，107.

[6]王明涛.多指标综合评价中权系数确定的一种综合分析方法[J].系统工程,1999(2):56-57.

[7]洪利华,罗均平,刘已斌. 基于主成分分析法的目标威胁评估[J]. 指挥控制与仿真,2006,28(2):49-52.

[8]张学工. 关于统计学习理论与支持向量机[J]. 自动化学报,2000(1):36-46.

Threat Target Evaluation of Air Targets to Warships in Air Defense Based on KPCA Method

LI Dong-lei, JIANG Li-ping

(Naval University of Engineering,Wuhan 430033, China)

The coming air targets threat evaluation and sorting of empty fire distribution of ships fire is important step.According to the characteristics of the coming air targets, after confirmed target index quantification, because nonlinear between each index of coming target, puts forward a method of using kernel principal component analysis feature extraction of target information, then based on the kernel principal components variance contribution to target threat assessment and sequencing. By simulation example, the results are more accurate and objective, effectively and avoided subjectivity strong problems in the traditional method, at the same time, the index data extraction process reduces the information dimension, reduces the computational complexity, provides a new way for warship air defense combat threat assessment.

threat evaluation; KPCA; warship air defense combat; air targets; variance contribution rate

1673-3819(2016)04-0032-04

2016-03-14

2016-04-13

国家自然科学基金(6107419);全军军事学研究生课题(2014JY451)

李冬雷(1991-),男,山东临沂人,硕士,研究方向为海军装备作战仿真和信息系统优化。

姜礼平(1962-),男,教授,博士生导师。

E917；E925.6

A

10.3969/j.issn.1673-3819.2016.04.007