基于灰色关联和D-S证据理论的导弹系统安全性评估

何小九，李彦彬，朱　枫，曹翊天

（空军工程大学防空反导学院，西安　710051）

基于灰色关联和D-S证据理论的导弹系统安全性评估

何小九，李彦彬，朱枫，曹翊天

（空军工程大学防空反导学院，西安710051）

针对导弹系统安全性评价的不确定性问题，提出了将灰色关联和D-S证据理论相结合的方法，从人员安全性、设备安全性和环境安全性建立了综合评估指标体系，用灰色关联分析处理了指标之间的关联性。在传统证据合成公式的基础上，考虑证据集非关键因素的权重，给出了修正的证据合成公式。并以打靶选弹为例进行了计算分析，得出了导弹安全性优先级排序，并将改进算法与传统计算方法的结果进行了比较，验证了评价模型的可行性与实用性，为导弹系统的管理工作提供了有益的参考。

D-S证据理论，灰色关联，导弹系统，安全性

0　引言

安全性是评价导弹武器系统使用质量“六性”（可靠性、维修性、保障性、测试性、安全性、环境适应性）中的一项指标，也是导弹武器系统研制、生产、使用和保障过程中的首要要求。GJB 451A［1］中对安全性有如下定义：安全性是指产品所具有的不导致人员伤亡、系统毁坏、重大财产损失或不危机人员健康和环境的能力。

对导弹系统的安全性进行评价，一方面可以采用定性分析的方法，如高成铭等［2］从导弹的各个组成部分来考虑，按照导弹系统的结构组成，分析导弹各个分系统的安全性；另一方面可以采用定量的方法，计算导弹武器系统的整体安全性，如江式伟［3］等采用粗糙集理论的方法，建立了评价导弹系统安全性的指标体系，对导弹的安全性进行了量化计算；高桂清［4］等采用了模糊数学和D-S证据理论，对导弹的安全性进行了评估。但由于“安全性”这个概念本身具有很强的模糊性，评价导弹系统的安全性并没有精确的数学计算方法。因此，在计算导弹系统安全性的过程中，要同时利用定性分析和定量计算的方法。采用灰色关联与D-S证据理论相结合的方法能对导弹系统的安全性进行较为准确的计算。

1　D-S证据理论

D-S证据理论（Dempster-Shafer Evidence Theory）是一种处理模糊性问题的评价方法，在信息融合［5-6］、故障诊断［7-8］、风险评价［9］等领域有着广泛的应用，也可用于系统的安全性评价［10］。与Bayes计算方法不同，证据理论在计算时可不考虑事件的先验概率，较适合用来计算武器系统的安全性。D-S证据理论有如下定义［11］：

定义1识别框架Θ。识别框架是对于评价问题的所有可能情形的集合，对该问题内的所有命题都是识别框架的一个子集。

定义2集函数m。若集函数m：2Θ→［0，1］（2Θ为Θ的幂集）满足条件：

则称集函数m是Θ上的一个基本可信度分配函数。其中A为命题，有A⊆Θ；m（A）为基本可信度，表示对命题或其任一真子集信任或支持的程度。该函数的值可以用一个区间来表示，区间下限称为信任函数（bel function），区间上限称为似然函数（pl function）。信任函数和似然函数的定义分别为：

定义3证据合成算法（evidential reasoning algorithm，也称Dempster合成规则）：

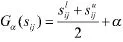
2　基于灰色关联和D-S证据理论的导弹系统安全性计算模型

根据GJB 451A中对安全性的定义，选择评价导弹系统安全性的3项指标：人员安全性、设备安全性、环境安全性并建立相应指标体系，如图1所示。

图1　导弹系统安全性评价指标体系

人员的安全性是指导弹系统由于各种工作情况对人体健康造成的伤害，危害终止能力是指当危险事件发生时，设备能自行终止并阻止危险发生的能力；设备的安全性是指在运行或待命状态时设备本身的安全度。环境安全性是指武器工作时对环境安全性产生的影响。

2.1构建区间判断矩阵

现有m个导弹系统A=｛A1，A2，…，Am｝，选取若干名有经验的专家对导弹安全性进行打分评判，则每个导弹系统在n项指标下得到n个命题。分数高低由专家查阅故障发生数据、状态监控数据、工作时间记录表后，再结合主观意见给出评分结果。打分采取10分制评分，分数越高，表明安全性越好，反之安全性越差。为避免端点出现单个坏值，选取次低分和次高分构成区间（sl，su），从而得到区间判断矩阵：

2.2矩阵归一化处理

由定义4选取合适的风险因子α，计算得到安全性矩阵G后，对其进行归一化处理，公式为：

把n个不同指标的权重ω=（ω1，ω2，…，ωn）代入到矩阵Y中得到加权隶属度矩阵：

2.3计算灰色关联系数

一般取ξ=0.5。得到综合灰色关联系数：

2.4计算不确定度

所选取指标Ij的q阶不确定度为：

一般取q=2，即欧氏距离。

2.5计算Mass函数

由式（8）得到第j个导弹系统Aj的Mass函数为：

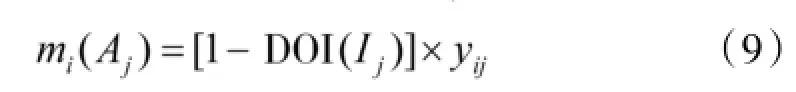
从而整体不确定度的Mass函数为：

2.6证据合成公式的改进

在对多个Mass函数进行合成时，一般选取定义3中的公式。但由于证据集中各因素的权重各异，该公式未考虑在证据合成时各因素权重的影响，而非关键因素权重在证据合成时应当弱化，因此，考虑证据集中的非关键因素，引入判断权重量值对因素权重进行处理。

选取识别框架中权重最大的因素，记为ωmax，则有ωmax=max｛ω1，ω2，…，ωn｝，ωi为某非关键因素的权重，由于该因素是非关键的，需要在证据合成时对其可信度进行调整。ωi调整后的Mass函数为：

则改进后的证据合成公式为：

由式（10）计算各导弹系统安全性的可信度，从而可以确定各个导弹系统的安全性优劣排序。

3　算例分析

现有5个导弹系统，要从中挑选3枚进行打靶试验。选取20名有经验的专家对导弹系统安全性进行评分，得到的综合评价结果如表1所示。

表1　各导弹系统评价结果

取α=0，将区间矩阵转化为单一值矩阵：

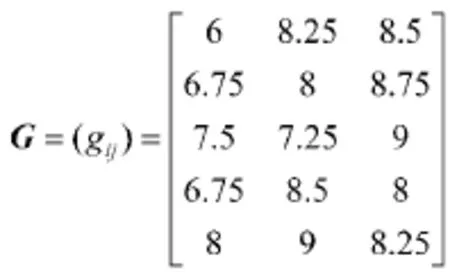
采用Delphi法，得到一级指标的权重为ω= （0.45，0.30，0.25），各二级指标的权重分别为ω1= （0.30，0.33，0.37），ω2=（0.22，0.24，0.11，0.13，0.30），ω3=（0.27，0.22，0.24，0.27）。将安全性矩阵归一化处理后乘以ω，得到加权后的标准化隶属度矩阵：

计算正理想点X+和负理想点X-，并计算最优关联系数、最劣关联系数：

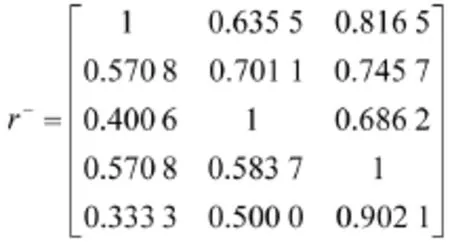
由式（7）计算关联系数矩阵：

由式（8）计算3个指标的不确定度：

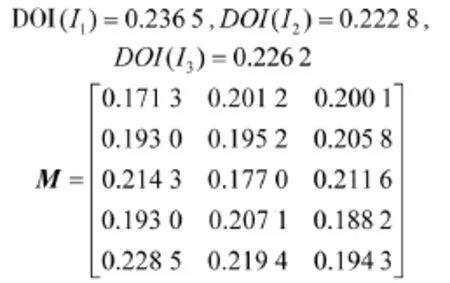
整体不确定度的Mass函数为：

m1（5）=0.225 4，m2（5）=0.268 9，m3（5）=0.277 6

运用改进后的证据合成公式，选取权重最小的3项指标对信任度矩阵进行修正处理。通过计算各指标的综合权重得到权重最小的3项指标分别为：湿度承受性、压力承受性、易燃性。最大权重的指标为危害终止能力，其综合权重为ωmax=0.166 5，运用新的证据合成公式求得修正后的可信度矩阵为：

从而求得识别框架内各子集的的信任函数值为：

运用传统证据合成公式进行计算，并将改进算法结果与传统算法进行对比，结果如图2所示。

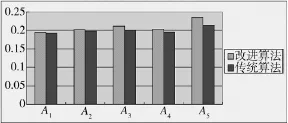
图2　改进算法与传统算法的结果比较

可见，采用修正后的证据合成公式时，5个导弹的安全性排序为：A5＞A3＞A4＞A2＞A1。A1系统的安全性最低，其系统安全性的支持度为19.46%；系统的安全性最高，其系统安全性的支持度为23.39%。因此，在选择导弹进行打靶试验时，应当选取A5、A3、A4三枚导弹作为试验弹。采用传统证据合成公式进行计算时，得出的安全性排序为：A5＞A3＞A2＞A4＞A1，与改进算法的计算结果有所不同。这是因为在证据合成时，弱化了非关键因素的影响。在使用过程中，应当重点关注A1导弹系统的安全性，妥善分析发生危险的主要方面，尽可能地避免安全事故。

4　结论

本文采用灰色关联和D-S证据理论相结合的方法，采用改进的证据合成公式对导弹武器系统的安全性进行了计算，是一种定性问题的定量计算方法。通过计算，得到了导弹系统的安全性评价值与优先级排序，并与传统方法进行了比较。结果表明，采用改进后的计算方法具有一定的有效性，评价结果是可信的，较好地解决了安全性评价的不确定性问题，拓展了灰色关联和证据理论的应用领域。同时为导弹安全性决策提供了一种评价与选择方法，对于导弹武器系统的安全管理工作有一定的参考意义。

［1］中华人民共和国国家军用标准GJB 451A.可靠性维修性保障性术语［S］.北京：中国人民解放军总装备部，2005.

［2］高成铭，张晓光，陶晓辉，等.某型导弹武器系统安全性分析［J］.质量与可靠性，2012，27（3）：17-19.

［3］江式伟，吕卫民，王亮.基于粗糙集的导弹安全性评估研究［J］.战术导弹技术，2010，31（3）：16-18.

［4］高桂清，刘风林，刘刚，等.基于D-S理论的常规导弹武器系统动态安全评价［J］.弹箭与制导学报，2007，27（1）：246-249.

［5］马丽娜，肖华勇，周旷.多源验前信息下基于证据理论的ML-II融合方法［J］.火力与指挥控制，2013，38（4）：121-124.

［6］宋建勋，张进，吴钦章.基于D-S证据理论的多特征数据融合算法［J］.火力与指挥控制，2010，35（7）：96-108.

［7］齐占伟，辜承林.基于改进的「DS证据理论在设备故障诊断中的应用［J］.海军工程大学学报，2008，20（1），60-64.

［8］林云，郜丽鹏.基于灰色关联和证据理论的故障诊断方法［J］.电子测量与仪器学报，2009，23（7）：68-72.

［9］CHEN L W，WANG W H，ZHANG W J.Risk evaluation of regional collapses geological hazard based on D-S evidence theory-A case study of haiyuan active fault belt in ningxia Province［J］.Energy Procedia，2012，16：371-376.

［10］项浩，姜礼平，刘涛.改进D-S证据理论的舰载弹库安全性评估［J］.火力与指挥控制，2011，36（11）：95-98.

［11］段新生.证据理论与决策、人工智能［M］.北京：中国人民大学出版社，1993：13-35.

Security Calculation of Missile System Based on Grey Relation and D-S Evidence Theory

HE Xiao-jiu，LI Yan-bin，ZHU Feng，CAO Yi-tian
（School of Air and Missile Defense，Air Force Engineering University，Xi'an 710051，China）

Considering the uncertainty question of missile system security assessment，the combination method of grey relation and D-S evidence theory is proposed in this paper.The security assessment index is established from human，equipment and environment.The relation of different indexes is handled by grey relation analysing.A modified evidential reasoning algorithm is given by considering the weight of unimportant factor in the evidence collection based on the traditional evidential reasoning algorithm.An example of choosing missile in shooting practice is calculated and analysed，the priority ranking of missile security is obtained.the improved calculation method and the traditional method is compared together to see the difference of result，which verified the feasibility and practicability of the evaluation model，and some beneficial

are provided for the future management work of missile system.

D-S evidence theory，grey relation，missile system，security

E927；TJ761

A

1002-0640（2016）07-0114-04

2015-05-15

2015-07-20

何小九（1992-），男，湖南邵阳人，硕士研究生。研究方向：国防采办与项目管理。