改进博弈论的舰载无人机编队协同对海突击目标分配*

韩玉龙，严建钢，陈　榕，李　俊，2，孙守福，林　云

（1.海军航空工程学院，山东　烟台　264001；2.解放军92913部队，海南　临高　571820）

改进博弈论的舰载无人机编队协同对海突击目标分配*

韩玉龙1，严建钢1，陈榕1，李俊1，2，孙守福1，林云1

（1.海军航空工程学院，山东烟台264001；2.解放军92913部队，海南临高571820）

目标分配问题是UAV自主控制的重要问题。针对舰载无人机编队协同对海突击目标分配问题，首先建立了基于离散动态贝叶斯网络的目标价值评估模型，在此基础上构建了舰载无人机编队的益损值矩阵，设计了舰载无人机编队协同对海突击目标分配的决策函数，提出了一种基于改进博弈论的目标分配方法，为4种不同约束条件下的目标分配问题分别设计了算法。最后对所建立的目标价值评估模型和改进博弈论的目标分配算法进行了实例仿真，仿真结果表明了模型和算法的可行性和有效性。

舰载无人机，对海突击，目标分配，贝叶斯网络，博弈论

0　引言

打击敌海上目标，夺取制海权是航母舰载无人机的主要使命任务之一。协同作战是舰载无人机的基本作战样式，航母舰载无人机编队协同对海突击作战包括对敌水面舰艇以及呈水面状态潜艇的进攻和防御，其目的是在敌方水面舰艇威胁危我方航母编队之前，发现、识别、标定并成功组织攻击，在确保航母编队安全的基础上，夺取制海权。

现代海战是网络化协同作战，舰载无人机编队利用数据链交换和共享作战信息，协同完成多目标攻击是未来海战发展的方向。为了使舰载无人机编队协同对海多目标突击的效率得到进一步提高，有必要深入研究舰载无人机编队对海突击目标分配的相关技术［1-2］。

1　基本概念和研究现状

目标分配问题的核心是如何把具有不同杀伤力和经济价值的武器，分配到射击不同的目标，构成整体的火力打击体系［3-4］。舰载无人机编队协同对海突击目标分配即在满足战术和技术指标、作战任务要求、舰载无人机及其武器系统性能等约束的前提下，将位置、价值和威胁不同的水上目标，按照一定的原则和策略，科学合理地分配给类型、价值和战斗力各不相同的舰载无人机，使得舰载无人机编队整体以最小代价获得最大作战效能。

目标分配的模型主要体现在目标函数和约束条件上，相应的求解方法也不尽相同，体现了处理问题的不同思路。满意决策方法是对穷举法的改进，将每个参与目标分配的个体看作一个Agent。个体Agent提出符合自己的满意集，把搜索空间限制在个体A-gent的满意集之内，舍弃不可行解与效率较低的分配策略，以此达到提高搜索效率的目的［5］。基于协同拍卖的方法通过买方竞价的方式实现资源的有效配置，可以获得较满意的分配结果，但整个过程耗时较长；基于合同网（Contract net protocol CNP）的方法采用多种合同类型，通过个体之间的协商和竞争机制，实现目标的分配和动态调整［6］；智能算法的兴起为大规模目标分配问题的解决提供了新的途径，遗传算法［7］、蚁群算法、粒子群算法［8］等在解决目标分配问题时具有较好的收敛速度，但也存在易陷入局部最优的缺陷。上述方法基本没有考虑攻防双方的对抗对目标分配的影响，文献［9-10］等将博弈论的思想引入目标分配，能够更加逼真地还原作战过程，在目标分配领域是一种非常有研究前景的方法。

本文在已有研究成果的基础上，针对舰载无人机编队协同对海突击目标分配这一热点问题，采用离散动态贝叶斯网络（Dynamic Bayesian Networks, DBN）方法实现对目标价值的实时评估，对传统目标分配模型和基于博弈论的方法进行一点改进，根据不同的战术原则，适应不同的目标分配约束。

2　舰载无人机编队协同对海突击目标分配数学模型

假设由舰载无人机组成的编队对敌水面舰艇目标进行突击，对问题进行简化，不考虑敌空中拦截，仅考虑水面舰艇预警雷达、舰炮和舰空导弹组成的防御系统。在卫星、预警机等信息保障下，进行舰载无人机任务规划，制定目标分配策略。

2.1舰载无人机益损值矩阵

假定有m架舰载无人机组成的编队对敌方n个不同类型水面舰艇目标进行突击。首先在卫星、预警机等平台的信息支援下获得态势数据，由航母编队指挥中心对敌水面舰艇目标价值进行评估，然后根据态势评估的结果构造编队目标分配决策函数。设vj为对目标进行实时评估并归一化后得出的目标相对价值（0＜vj≤1，j=1,2，…，n），pij为第i架舰载无人机对第j个水面舰艇目标的杀伤概率，那么第i架舰载无人机攻击第j个目标时获得的收益为eij=f （vj，pij）=vj·pij，第i架舰载无人机攻击各个目标时获得的收益为ei=g（ei1,ei2，…，ein），各架舰载无人机对攻击各个目标获得收益如式（1）。

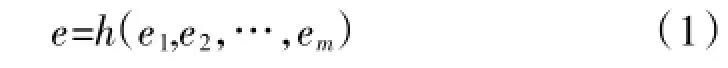
ui为我方舰载无人机归一化后得出的价值（0＜ui≤1，i=1,2，…，m），qij为第i架舰载无人机被第j个水面舰艇目标反击时的杀伤概率，那么第j个目标反击第i架舰载无人机时获得的收益为cij=f（ui，qij）=ui·qij，第j个目标反击各架舰载无人机时获得的收益c·j=g（c1j,c2j，…，cmj），各目标反击各架舰载无人机获得收益也即各舰载无人机编队攻击各敌方目标的损失如式（2）。

构造基于攻防对抗双方博弈的目标分配决策函数ρ（e，c）。

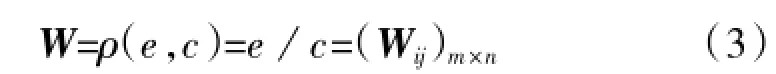
W为舰载无人机编队攻击敌方目标的益损值（收益损失比）矩阵，为第i架舰载无人机攻击第j个目标时获得的收益与所付出代价的比值，其中，i= 1,2，…，m，j=1,2，…，n。由上述定义易知，对于敌方水面舰艇编队来说，W是其损益值（损失收益比）矩阵。

2.2基于离散DBN的目标价值评估

目标的价值是随时间的变化而变化的，对目标价值的实时评估也就为目标的实时分配奠定了基础。水面舰艇目标的移动速度相对较慢，因而对其预警探测相对容易；舰载无人机具有速度大、隐身性能好等特点，敌方在对我舰载无人机进行价值评估时，对初始值的依赖较大。作为我方决策者来讲，对敌方目标不可能完全了解，需要实时探测。而模拟敌方评价我方舰载无人机的价值时，不知道敌方对我方装备的熟悉程度，按照最不利的情形，即敌方对我方舰载无人机装备完全了解。本文采用离散DBN模型方法对目标的价值进行评估［11］。

2.2.1网络结构

贝叶斯网络的网络结构式表示条件独立性信息的一种自然方式，网络中的每个结点都表示特定域中的一个变量，结点间的连接（有向弧）表示相互间因果关系，体现了领域知识性方面的特征。建立目标价值评估离散DBN模型需要首先确定其网络结构［12］。

对于舰载无人机编队来说，目标价值体现在固有价值（Int）和体系价值（Sys）两个方面。其中，目标的固有价值，又可以从经济价值（Eco）、政治价值（Pol）和心理价值（Psy）3个方面进行刻画。而目标的体系价值，需要充分考虑目标在整个目标体系中的地位和作用，可分为关键结点（Key）、重要结点（Imp）以及普通结点（Gen）。通过上述分析，建立基于离散DBN的目标价值评估网络模型。

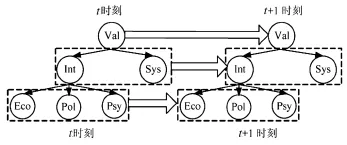
图1　目标价值评估网络模型

目标价值分析模型中，各结点变量的状态集合可表示为：目标价值（Val）=｛高（H），中（M），低（L）｝；目标经济价值（Eco）=｛高（H），中（M），低（L）｝，目标的政治价值（Pol）=｛高（H），中（M），低（L）｝，目标心理价值（Psy）=｛高（H），中（M），低（L）｝；目标的体系价值（Sys）=｛关键结点（key），重要结点（Imp）,普通结点（Gen）｝。

2.2.2构造条件概率表

建立了基于离散DBN的目标价值评估网络模型以后，需要构造条件概率表。条件概率表的建立要综合多方面的海战场信息，同时还要考虑军事专家的建议，也可以对经验数据进行统计学习来获得。

对于图1建立的离散DBN目标价值评估模型，建立条件概率表如表1和表2所示。

表1　条件概率表（1）

表2　条件概率表（2）

2.2.3目标价值归一化

对于该模型，可利用Netica软件进行仿真计算，得到每个目标的绝对价值。在此基础上，对目标价值进行归一化。

2.3指标函数

在分配目标时根据不同的分配原则，可以设定不同的指标函数。“保存自己，消灭敌人”，目标分配的首要原则就是益损值最优。因此，目标分配的指标函数为：

3　基于改进博弈论的舰载无人机编队协同对海突击目标分配算法

文献［13］提出了改进矩阵法的无人机编队内目标分配算法，但是仅从己方的角度出发，忽略了敌方针对我方目标分配可能采取的反击策略；文献［9］从攻防对抗双方的角度提出了基于博弈论的目标分配方法，但是该算法为避免目标重复分配，仅考虑了每个目标只能分配给一架舰载无人机这样一个特殊的情况，而实际上，有些情况下一架舰载无人机无法达成对某个目标的突击企图。基于此，本文针对不同的分配约束设计不同的算法，以适应舰载无人机编队协同对海突击目标分配的需要。该算法的基本思路是：首先进行目标价值评估，建立舰载无人机编队益损值矩阵，然后根据不同的约束条件确定对应的选取规则寻找符合要求的元素，并在每一次选取之后考虑敌方的应对策略，这样依次为每一架舰载无人机分配目标［14］。

3.1约束1：舰载无人机可攻击多个目标且目标可以重复分配

Step1进行目标价值评估，建立益损值矩阵W。

Step2为第1架舰载无人机选择攻击目标。从益损值矩阵中寻找最大元素，如果有相同元素则随机任选一个。记下i和j的标号，即由舰载无人机Ui攻击敌方水面舰艇目标Sj，记作Ui→Sj。

Step3调整益损值矩阵，确定攻击Ui的目标。将元素所在行和列元素分别乘以益损值下降系数β，β∈［0，1］，β=0表示该水面舰艇目标完全毁伤；β=1表示该水面舰艇目标完全没有毁伤。在第i行中搜索最小的非零元素ia，即敌方会派出目标Sa对Ui进行拦截，记作：Sa→Ui。

Step4调整益损值矩阵，确定攻击目标Sa的舰载无人机。将元素ia乘以益损值下降系数β。在益损值矩阵第a列中寻找最大的元素ca，记下标号c 和a，即舰载无人机Uc攻击敌方水面舰艇目标，记作：Uc→Sa。

Step5判断所有舰载无人机是否都已达到最大分配目标数。如果已达到，则停止。否则，重复Step3～Step5。

Step6选取分配结果。按照益损值最大的原则进行选取，对分配结果进行优化提取。

3.2约束2舰载无人机可攻击多个目标且目标不可重复分配

算法在约束1基础上对Step3～Step5作以下调整：

Step3调整益损值矩阵，确定攻击Ui的目标。将元素所在行和列的元素乘以益损值下降系数β。在第i行中搜索最小的非零元素ia，即敌方会派出目标Sa对Ui进行拦截，记作：Sa→Ui。

Step4调整益损值矩阵，确定攻击目标Sa的舰载无人机。将元素所在行和列元素分别乘以益损值下降系数β。在益损值矩阵第a列没有被分配过目标Ma的舰载无人机中寻找最大的元素ca，记下标号c和a，即舰载无人机Uc攻击敌方水面舰艇目标Sa，记作：Uc→Sa。

Step5判断所有目标分配是否完成。如果完成，则停止。否则，则重复Step3～Step5的过程，直至所有目标分配完成。

3.3约束3舰载无人机仅能攻击一个目标且目标可以重复分配

算法在约束1基础上对Step3～Step5作以下调整：

Step3调整益损值矩阵，确定攻击Ui的目标。将元素所在行和列的元素乘以益损值下降系数β。在第i行中搜索最小的非零元素（iaa=1,2，…，n且a≠j），即敌方会派出目标Sa对Ui进行拦截，记作：Sa→Ui。

Step4调整益损值矩阵，确定攻击目标Sa的舰载无人机。将元素ia乘以益损值下降系数β。在益损值矩阵第a列没有被分配过目标的舰载无人机中寻找最大的元素ca，记下标号c和a，即舰载无人机Uc攻击敌方水面舰艇目标Sa，记作：Uc→Sa。

Step5判断所有舰载无人机是否都已分配目标。如果是，则停止。否则，则重复Step3～Step5的过程，直至所有舰载无人机都已分配到目标。

3.4约束4舰载无人机仅能攻击一个目标且目标不可重复分配

算法与3.1基本相同，由于分配原则不同，对Step3～Step5作以下调整：

Step3调整益损值矩阵，确定攻击Ui的目标。将元素所在行和列的元素乘以益损值下降系数β。在第i行中搜索最小的非零元素（a=1，2，…，n且a≠j），即敌方会派出目标Sa对Ui进行拦截，记作：Sa→Ui。

Step4调整益损值矩阵，确定攻击目标Sa的舰载无人机。将元素ia乘以益损值下降系数β。在益损值矩阵第a列搜索没有被分配过目标的舰载无人机中寻找最大的元素ca，记下标号c和a，即舰载无人机Uc攻击敌方水面舰艇目标Sa，记作：Uc→Sa。

Step5判断所有目标分配是否完成。如果完成，则停止。否则，则重复Step3～Step5的过程，直至所有目标分配完成。

4　仿真算例和结果分析

4.1仿真算例

假定我预警机探测到敌方由驱逐舰、护卫舰等6搜水面舰艇组成的编队向我航母方向航行，我舰载航空兵指挥所接到航母编队指挥所命令，可派出由9架舰载无人机组成的编队对敌水面舰艇编队进行突击。

首先对敌方目标的价值进行评估。

对模型进行初始化，在获得进一步目标信息前，无法对目标价值进行判断，为了保证其后的评估不带有任何倾向性，假定某目标在初始时刻的目标价值状态为Value［High,Middle,Low］=［33.3 33.3 33.3］，也就是目标价值处于高、中、低3个状态的概率相同，如下页图2所示。

对目标1，通过侦察探测兵力的实时侦察，得出了如表3所示目标1三个时刻的影响因子值。

表3　目标1三个时刻的影响因子值

将目标1的相关参数输入模型中，得到的推理结果如下页图3～图5所示。

图2　模型进行初始化示意图

图3　1时刻目标1价值评估结果

图4　2时刻目标1价值评估结果

图5　3时刻目标1价值评估结果

图6　4种约束条件下程序运行时间（s）

将实验参数代入到建立的离散DBN模型中进行仿真，仿真结果如图5～图6所示，可以得到0，1，2，3时刻目标1的优先级为高的概率分别为33.3%，45.9%，53.7%，58.8%，为体现目标评估的实时性，将目标1价值为高的概率确定为58.8%。以此类推，计算出所有目标价值为高的概率为［0.588，0.645，0.344，0.675，0.568，0.900］，经过归一化，得到目标价值的归一化值为V=［0.158 1，0.173 4，0.092 5，0.181 5，0.152 7，0.241 9］。

我方舰载无人机的归一化价值直接给出，S= ［0.154 3，0.171 5，0.024 1，0.172 9，0.119 8，0.018 4，0.052 7，0.103 6，0.182 7］。各舰载无人机对每个目标的毁伤概率和各目标对我舰载无人机的毁伤概率分别如表4和表5所示。根据式（1）～式（4）得到舰载无人机编队的益损值矩阵如表6所示。

表4　各舰载无人机对各目标的毁伤概率

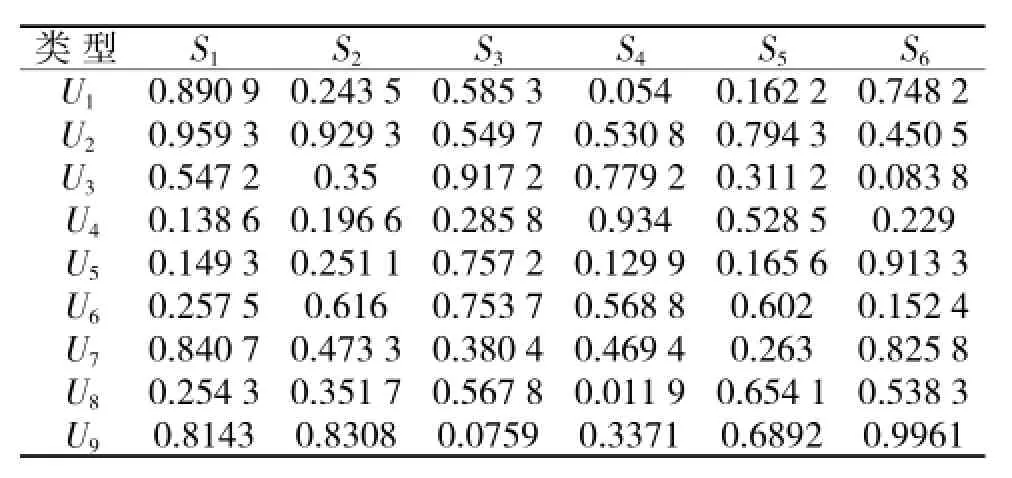
表5　各目标对各舰载无人机的毁伤概率

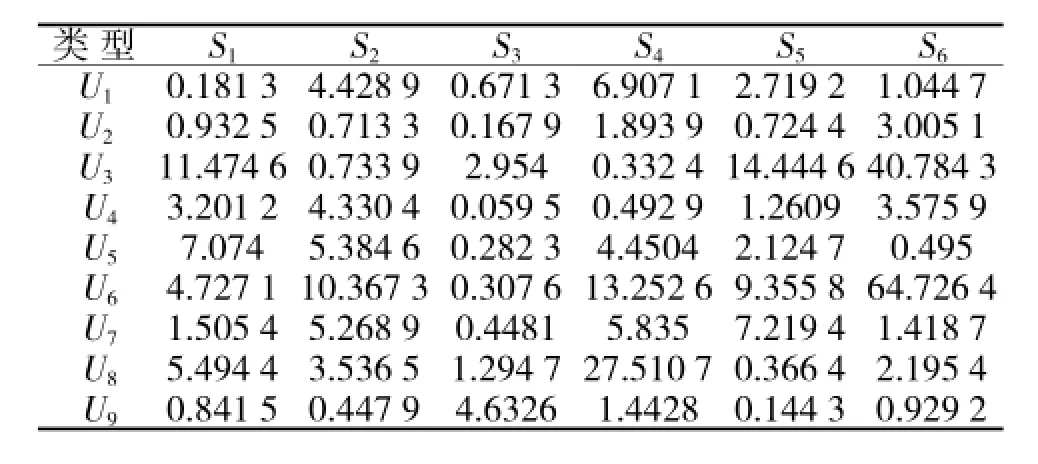
表6　各舰载无人机突击各目标的易损值

运用基于改进博弈论的舰载无人机编队协同对海突击目标分配方法，对4种不同原则下的目标分配情况分别进行仿真，益损值下降系数取为0.5，通过Matlab7.6编程仿真，仿真结果如表7～表10所示，0表示没有分配目标。

表7　舰载无人机可分配多个目标且目标可重复分配

表8　舰载无人机可分配多个目标且目标不能重复分配

表9　舰载无人机可分配一个目标且目标可重复分配

表10　舰载无人机可分配一个目标且目标不可重复分配

4.2结果分析

分别对4种分配原则下的目标分配结果进行分析。在舰载无人机可攻击多个目标且目标可重复分配的约束下，从表7的分配结果看，按照益损值最优的原则，所有舰载无人机都达到了最大目标分配数，所有目标都已分配完毕，并且被攻击的次数都不少于2次；在舰载无人机可攻击多个目标且目标不能重复分配的约束下，从表8的分配结果看，按照舰载无人机U3，U6分别分配了两个目标，而U1，U2，U4，U5，U7没有分配目标，这是由于在目标不可被重复分配的限制下追求益损值最优，如果改变分配策略，则会使益损值下降，这是没有被分配的目标的舰载无人机可对编队内的其他成员进行支援与掩护；在舰载无人机仅能攻击一个目标且目标可重复分配的约束下，从表9的分配结果看，所有舰载无人机都分配到了一个目标，S3、S5分别被分配给了3架舰载无人机；在舰载无人机仅能攻击一个目标且目标不可重复分配的约束下，从表10的分配结果看，所有舰载无人机都分配到了一个目标，每个目标也分别被分配给了一架舰载无人机。算法的运行时间从图6可以看出，都能保证在0.01 s内完成目标分配，符合舰载无人机编队协同对海突击实时性的要求，不同的约束条件体现着不同的战术原则，结果合理可信。

5　结论

舰载无人机编队协同对海突击目标分配问题是舰载无人机编队协同对海突击任务规划中的重要环节。本文在对其概念和研究现状进行研究的基础上，提出了基于改进博弈论的目标分配方法，并针对其中的目标价值评估问题，构建了基于离散DBN的目标价值评估方法，对4种约束条件下的目标分配情况分别设计了算法，仿真结果表明算法可行有效，可以为指挥员提供辅助决策。实际上，在目标分配的过程中，不仅反映了攻防双方的对抗特点，也体现了一定的时序特征。但该方法的前提是攻防双方完全理性，且对对方的装备非常了解，这在实际作战中可能过于理想，下一步需要研究在信息不完全情况下的目标分配问题。

［1］梁国伟，王社伟，赵雪森.多无人机协同任务分配方法［J］.火力与指挥控制，2014，39（11）：13-17.

［2］罗贺，王国强.基于Agent的多无人机任务分配模型［J］.火力与指挥控制，2014，39（7）：22-26

［3］陈闽.编队协同作战目标分配建模综述［J］.电光与控制，2013，20（9）：53-58.

［4］李勇君，黄卓，郭波.武器—目标分配问题综述［J］.兵工自动化，2009，28（11）：1-4.

［5］叶媛媛，闵春平.基于满意决策的多UAV协同目标分配方法［J］.国防科技大学学报，2005，27（4）：116-120.

［6］唐苏妍，梅珊，朱一凡，等.基于扩展合同网协议的分布式武器目标分配方法［J］.系统工程与电子技术，2011，33 （3）：568-574.

［7］罗红英.遗传算法在目标优化分配中的应用［J］.电光与控制，2008，15（3）：18-20.

［8］范成礼，邢清华.基于IDPSO的武器目标分配优化算法［J］.系统工程与电子技术，2015，37（2）：336-342.

［9］唐传林，杜海文.基于博弈论的多UCAV对地攻击目标分配［J］.电光与控制，2011，18（10）：28-31.

［10］曾松林，王文恽，丁大春，等.基于动态博弈的目标分配方法研究［J］.电光与控制，2011，18（2）：26-29.

［11］史建国，高晓光，李相民.基于离散模糊动态贝叶斯网络的空战态势评估及仿真［J］.系统仿真学报，2006，18 （5）：1093-1096.

［12］史建国.变结构离散动态贝叶斯网络的快速推理算法［J］.火力与指挥控制，2012，37（9）：71-74.

［13］杨涛，周德云.改进的无人机编队内目标分配算法研究［J］.计算机测量与控制，2008，16（11）：1641-1643.

［14］张琳，马良，万新龙.改进遗传算法的多机超视距同空战目标分配法［J］.四川兵工学报，2013，24（1）：154-157.

Improved Game Theory Based Targets Assigning for Ship-based UAV Formation Coordinated Air-to-Sea Attack

HAN Yu-long1，YAN Jian-gang1，CHEN Rong1，LI Jun1，2，SUN Shou-Fu1，LIN Yun1
（1.Naval Aeronautical and Astronautical University，Yantai 264001，China；2.Unit 92913 of PLA，Lingao 571820，China）

Target assigning is an important problem for autonomous control and management of cooperative UAVs.To resolve targets assigning for Ship-based UAV Formation coordinated Air-to-Sea attack，a target value assessment model base on discrete Dynamic Bayesian networks（DBN）is proposed，on the basis of which the profit and loss matrix is formed.Then a decision function and an improved game theory based model of targets assigning for Ship-based UAV formation coordinated air-to-sea attack are proposed.Four special kinds of algorithm are designed for corresponding restriction.Lastly，the improved game theory algorithm is simulated.The experimental results shows that the method can quickly and efficiently resolve the target assigning problem for Ship-based UAV formation coordinated air-to-sea attack.

ship-based UAV，air-to-sea attack，targets assigning，Bayesian networks，game theory

TP391；TJ85

A

1002-0640（2016）07-0065-06

2015-05-20

2015-07-15<* class="content">*基金项目：国家社会科学基金军事学项目（11GJ003074）；军事学博士研究生基金资助项目（2014JY473）*

国家社会科学基金军事学项目（11GJ003074）；军事学博士研究生基金资助项目（2014JY473）< class="content">作者简介：韩玉龙（1987-），男，山东潍坊人，博士研究生。研究方向：武器装备攻防体系对抗和信息化，舰载无人机作战使用。

韩玉龙（1987-），男，山东潍坊人，博士研究生。研究方向：武器装备攻防体系对抗和信息化，舰载无人机作战使用。