基于变值法的船型优化层次分析法模型研究
2016-08-18陈建平黄鹏举徐艳敏广州航海学院船舶工程学院广东广州50725上海交通大学船舶海洋与建筑工程学院上海200240广东工业大学自动化学院广东广州50006
陈建平,徐 洁,龚 幼,黄鹏举,徐艳敏(. 广州航海学院 船舶工程学院,广东 广州 50725;2. 上海交通大学 船舶海洋与建筑工程学院,上海 200240;. 广东工业大学 自动化学院,广东 广州 50006)
基于变值法的船型优化层次分析法模型研究
陈建平1, 2,徐洁3,龚幼1,黄鹏举1,徐艳敏1
(1. 广州航海学院 船舶工程学院,广东 广州 510725;2. 上海交通大学 船舶海洋与建筑工程学院,上海 200240;3. 广东工业大学 自动化学院,广东 广州 510006)
采用层次分析法理论和变值法,提出船舶船型技术经济性层次分析方法,建立起船舶船型经济评价的层次分析数学模型。通过对珠江干线 3 000 吨级散货船的船型进行实例研究分析,得出了船型优化综合评价指标的排序,得出综合最优船型。在此基础上,对影响船型方案的参数进行敏感性分析。本文提出的船型方案层次分析的经济评价方法,对优化船型的优化设计具有理论研究和实用价值。
船型优化;层次分析法;变值法;敏感性分析
0 前 言
在现代船舶设计中,特别是对于民用运输船舶来说,它不仅要符合设计要求,具有良好的技术性能,而且要充分重视船舶的经济性能。在设计和建造 1 艘新的船舶,对于一个给定的运输任务,有不同的设计方案,但这些技术的经济效果是不一样的。通过对各种技术方案的经济效果的评价,可以采用先进的技术、可靠的、经济的性能来选择最佳的设计方案。相反,如果片面追求的“先进”被认为是在设计过程中的技术指标,而忽略了船舶的经济性,这将导致设计不合理,造成船舶营运的经济失误。这种类型的船舶设计失败在船舶设计实践中是经常出现的。
船舶主尺度优化目标函数是非线性函数,优化变量主要包括主尺度、船型系数、转速和发动机功率等。船舶的船型优化问题是一个多目标决策问题[1-4]。建立多目标系统的综合评价指标的方法有很多,如加权法、分层序列法、理想指标规划等[5-8]。由于不同目标函数之间的可比性和相互冲突,多目标优化问题不仅仅是一个纯粹的客观标准问题,更是一个为多目标决策问题选择客观标准的问题[9-10]。如何建立一个好的决策标准是多目标决策的关键。选择不同的目标函数或权重,优化结果往往不同。所以决策结果往往带有相对性和主观性,不能真实反映客观事实。
采用层次分析法对多目标优化设计方案建立起相应的数学模型,采用变值法(网格法)来解决多目标优化调度问题。最后通过对珠江干线某吨级散货船的船型优化实例,来验证文章所提方法的有效性。
1 船舶技术和经济性评价
1)初始数据处理。对船舶的类型、营运、造价等方面进行收集调查,对原始数据进行分析,得出船舶技术经济参数的评价过程
2)船舶多方案技术和经济指标计算。根据船舶运营实际情况,确定典型的航线和典型的船舶吨位、船型方案的性能计算。
3)船舶类型评价。首先确定船舶技术综合评价指标,然后根据评价指标,采用多目标综合评价法对船舶技术经济综合评价指标进行综合评价。
4)确定最佳船型。根据船舶综合排序的结果,确定船舶类型和典型船型。
5)敏感性分析。对典型船型的技术经济指标进行敏感性分析。
2 船型优化模型
2.1层次分析法
层次分析法(AHP)方法由美国著名科学家 Satty T.L.等在 20 世纪 70 年代中期提出[11-13]。层次分析法是一种多指标决策方法,根据决策问题的性质和总目标,将复杂问题分解为一个自底向上的层次结构,然后根据分解的层次,对决策方案进行排序。层次分析法作为一种决策工具,具有明显的优势,其适用性强。层次分析法是基于问题的系统组成,它研究问题系统的各个组成部分之间的相互联系以及与系统外环境的关系。层次分析法已应用于经济分析、规划、能源、资源政策分析、企业管理、社会科学、建筑、医疗卫生等诸多领域[14]。
船舶技术与经济综合评价是一项多准则决策问题,包含定量计算也有定性分析。层次分析法将定性分析与定量分析进行有机结合,将船型优化问题分解为相互关联有序的层次结构,构造基于其相对重要性的各层次判断矩阵,利用排序权向量的特征根法来确定各层次各元素的权重。最后,通过计算各层元素的组合权重,确定层次的总排序,最后得出综合指标最优的船型方案。
2.2建立模型
2.2.1构建模型层次
所有要素分为目标层、准则层和方案层 3 个层次。顶层是目标层,表达要解决问题的目的,是实现决策问题的目标。中间层是标准层,以实现目标为目标,采取的措施和指导方针。底层是一个计划层,显示出各种各样的选择,参与选择的最佳决策。
2.2.2构建判断矩阵
判断矩阵是层次分析法的基础,各元素的数值反映了问题中各因素的相对重要性。为了形成一个判断矩阵,采用 1 ~ 9 及其倒数作为标度方法,然后将元素进行两两比较,可以得到判断矩阵。
当船型方案作为准则层的各项技术经济指标确定后,可以通过采用两两比较船型指标而得到判断矩阵A-B 的各元素。判断矩阵 A 是一个正互反矩阵,一般构造为 A = (aij)m × n,其中 m 为准则数(船型方案影响指标数)它具有以下特性
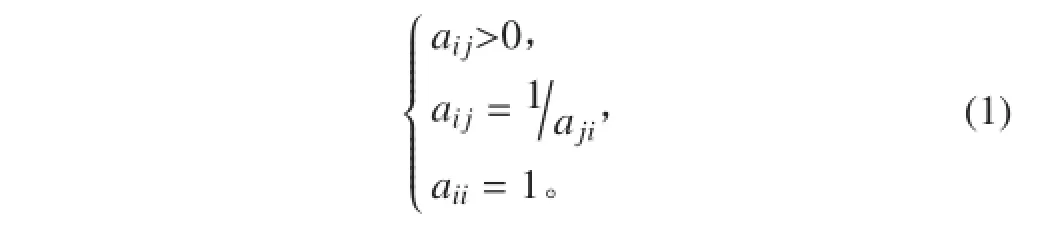
2.2.3层次单排序及其一致性
在构建了决策问题的层次模型和判断矩阵之后,船型优化经济性问题转化为一个要素排序问题。判断矩阵 A 可以通过对元素 A1,A2,…,Am的两两比较得到,这样可以获得层次的单排序。对于该层次上层某元素,本层次中与之有联系的元素的权重随之可以通过计算判断矩阵 A 的特征值和特征向量来获得,即满足关系式
式中:λmax为判断矩阵 A 的最大特征根;V 为经正则化的特征向量,它的分量 Vi为元素 A1,A2,…,Am在准则下的排序权重。
在层次分析法中,保持矩阵的一致性非常重要。当 m 阶判断矩阵 A 中的元素有以下关系时,判断矩阵被认为是一致的:
在不满足一致性条件的情况下,相应的特征根λmax也将发生变化,从而影响到层次排序的结果。

表1 1~9 阶判断矩阵 RI 值Tab. 1 Mean random consistency index of judgment matrix
2.2.4层次总排序和一致性检验
进一步计算层次总排序,是通过计算同一层次中所有因子对目标层的相对重要性的排序权重来完成的。这个过程是由最高级别到最低级别逐层进行,如果上层 A 包含 m 个因子 A1,A2,…,Am,其层次总排序权重分别为 B1,B2,…,Bn,它们对于任意因素 Aj的单层次的排序权重分别是 b1j,b2j,…,bnj,那么 B的最终排序权重可以通过表2计算得到。
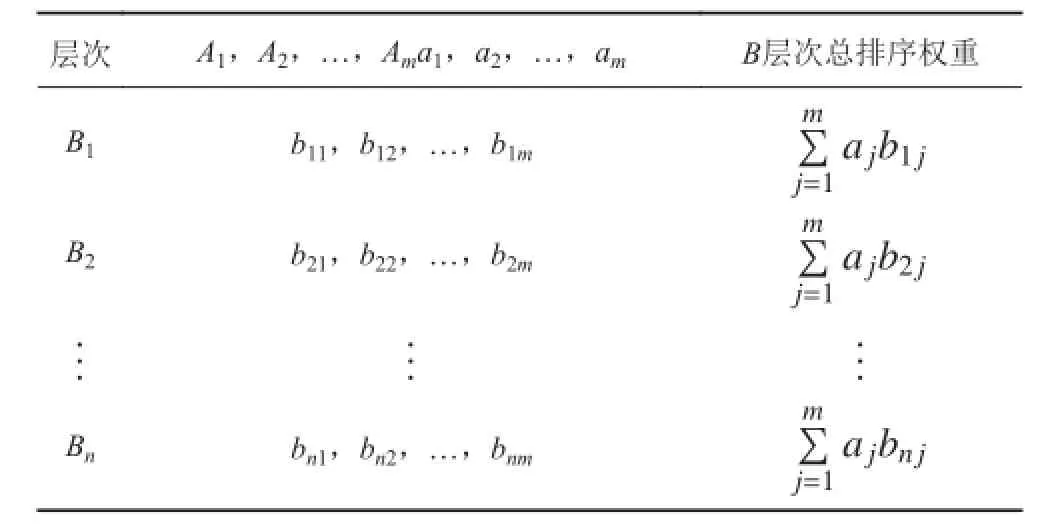
表2 总排序计算表Tab. 2 Total sorting table
同样需要由高到低对层次总排序进行一致性检验。如果层次 B 因素对于单排序 Aj的一致性指数为CIj,对应的平均随机一致性指数为 RIj,那么层次 B 最终总排序的随机一致性值为
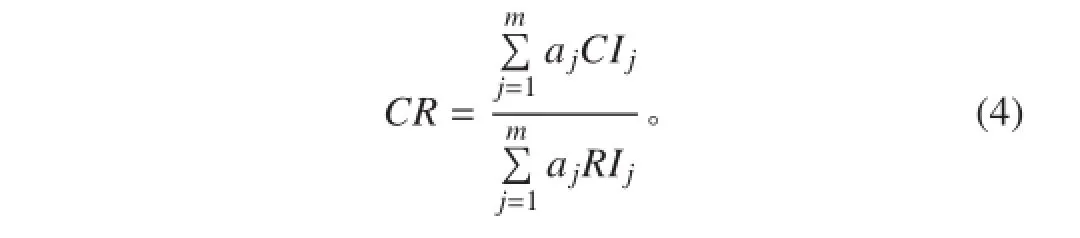
当 CR<0.10,即认为总排序结果满足一致性。
3 算 例
为验证文章方法的适应性和正确性,文章选取了航行于珠江干线 3 000 t 干散货船来进行实例研究。根据珠江干线航道的实际情况,选择表3 中参数作为基本参数。
3.1船型参数选取
求取主要相关船型参数。方形系数:
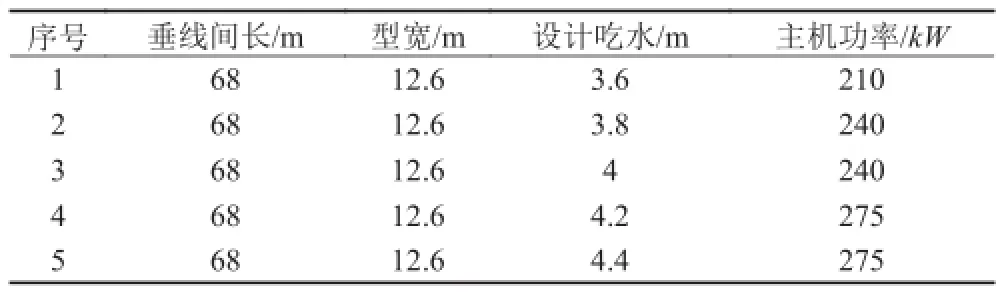
表3 船舶基本参数Tab. 3 Ship basic parameters
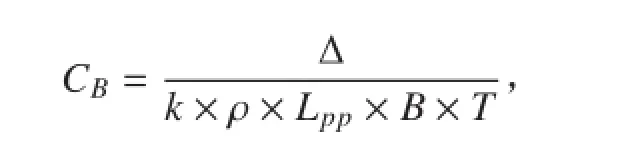
式中:Δ为排水量;k 为附体体积系数;ρ 为水的密度;Lpp为垂线间长;B 为型宽;T 为吃水。
载重量:
DW=IDWRCW×CW,
式中:IDWRCW 为载重量与载货量之间的比值,可以由母型船求得;CW 为载货量。
海军系数法求速度:
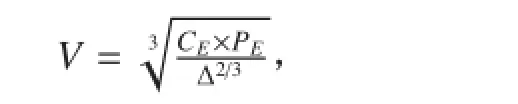
式中:CE为海军系数;PE为主机功率;Δ为排水量。
船舶造价:
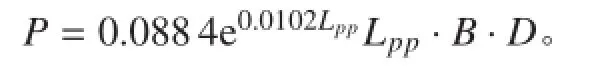
年载货量:

投资回收期:
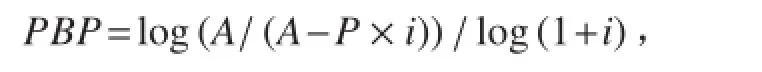
式中:A 为年收益;i 为贷款利率;P 为船舶造价。净现值:
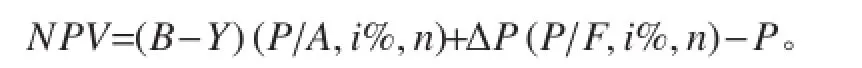
3.2变值法(网格法)构造船型方案
参数化分析也被称为变值法或网格法。其基本原则是:首先在船舶的主尺度范围内形成一系列的设计变量,根据船舶使用的要求和船舶主要尺度的限制,允许改变船舶的主要尺寸范围;然后,采用整体组合的方法,形成一系列的船型方案,并计算每个方案的技术和经济性能。在此基础上,根据船舶方案的评价指标,优选出船舶方案的设计方案。采用变值法构造了一系列的船型方案,如表4 和表5 所示。
3.3计算结果
根据模糊决策模型,计算船型评价指标,计算结果如表6 和表7 所示。
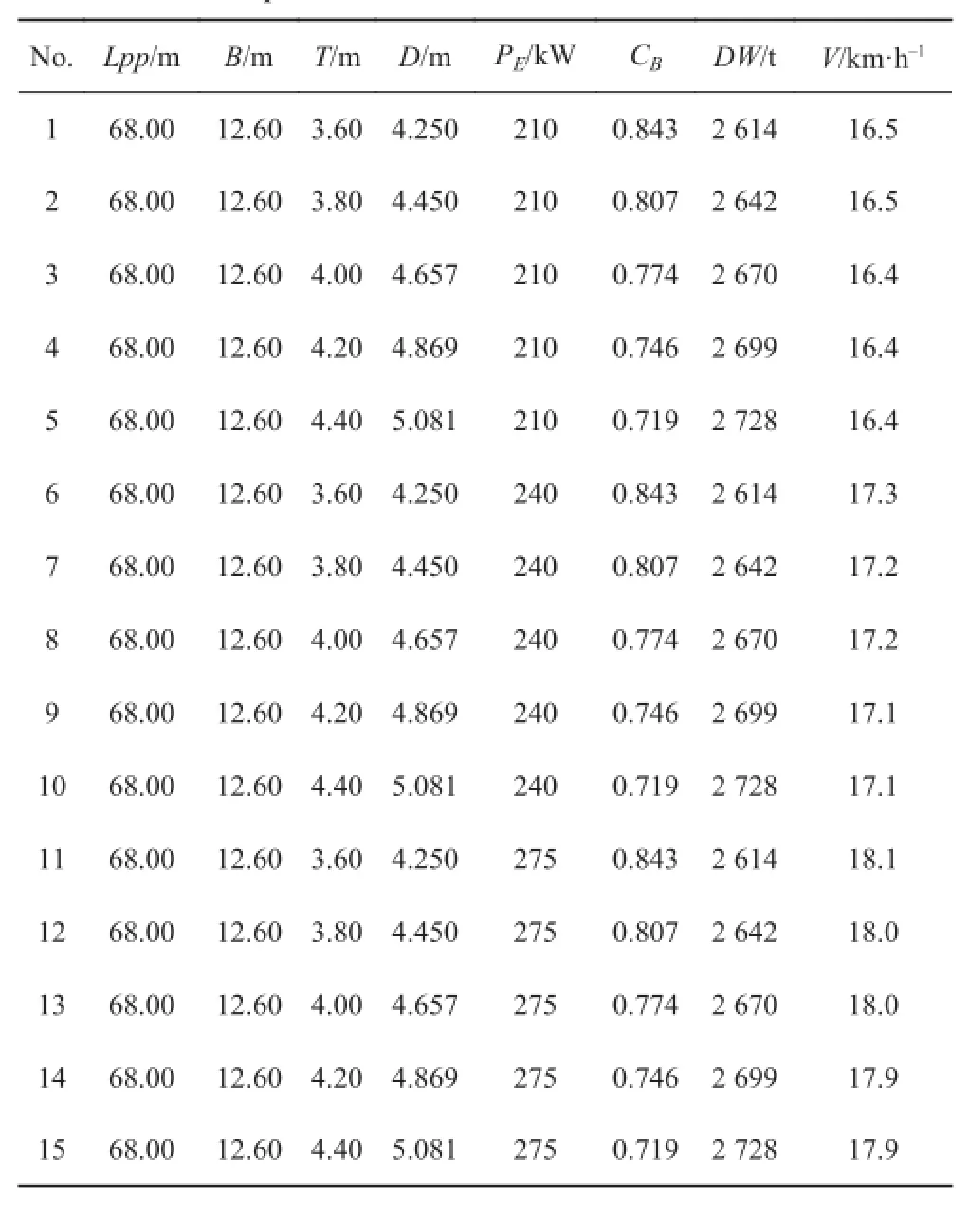
表4 变值法构造船型方案 1Tab. 4 Ship form scheme with variable value method 1
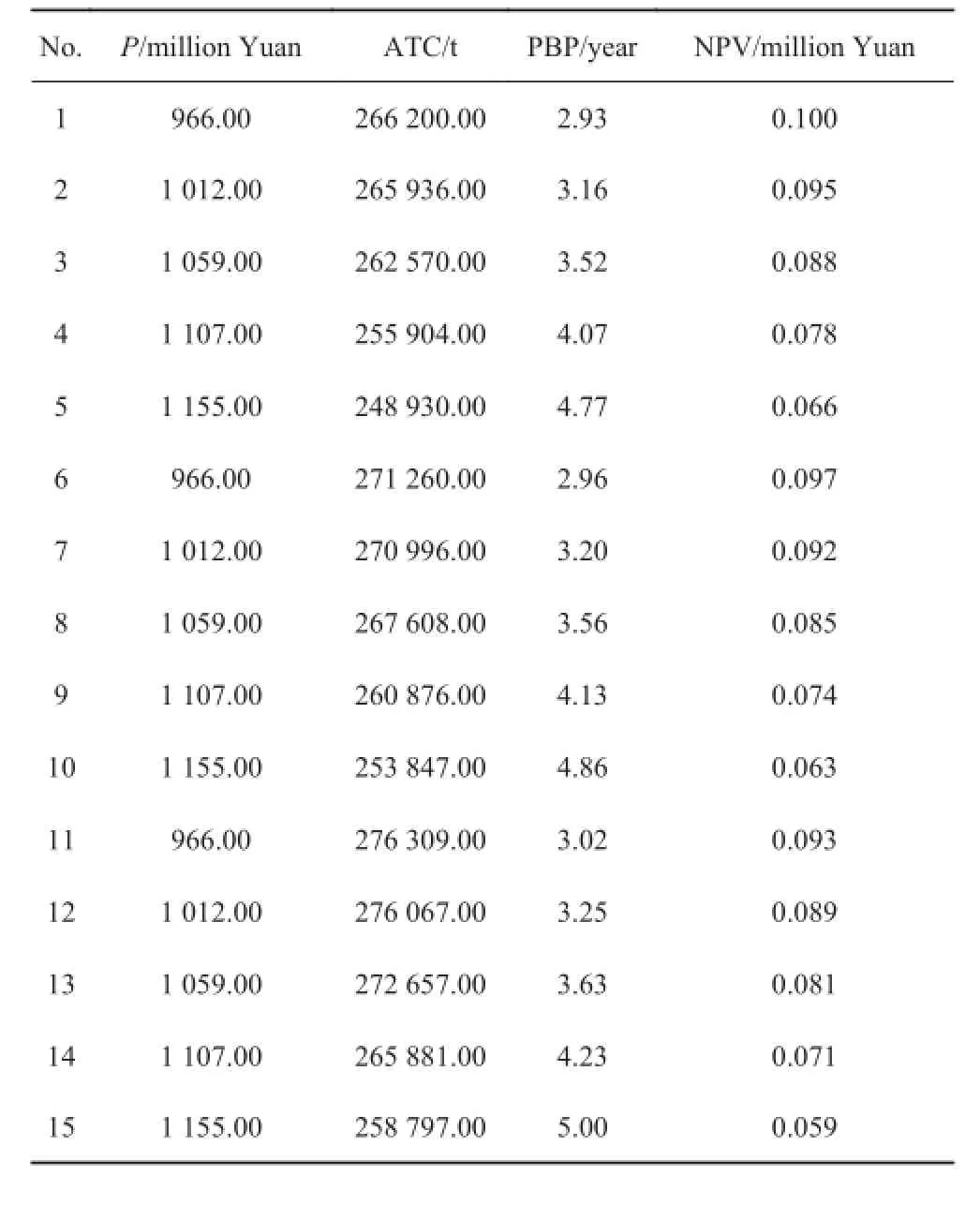
表5 变值法构造船型方案 2Tab. 5 Ship form scheme with variable value method 2
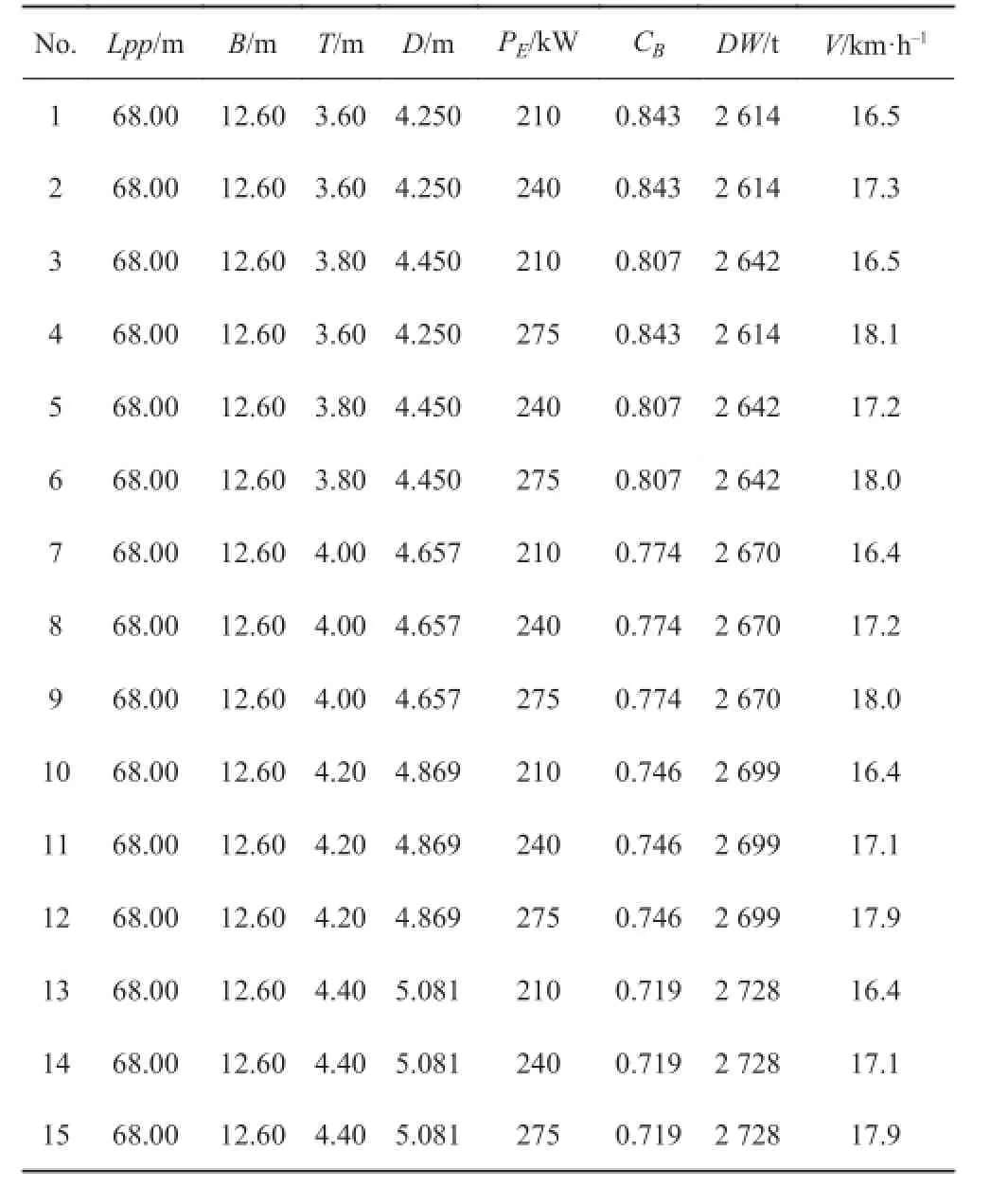
表6 船型评价指标计算结果 1Tab. 6 The evaluation index ranking 1
表7 船型评价指标计算结果 2Tab. 7 The evaluation index ranking 2
根据表6 和表7,可以对净现值(NPV)和投资回收期(PBP)进行比较分析,得到图1 和图2。水平坐标为船舶自重,纵向轴线为评价指标。
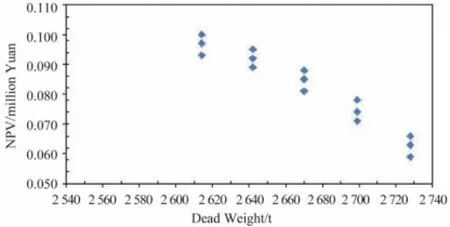
图1 净现值(NPV)分布Fig. 1 The distribution of NPV
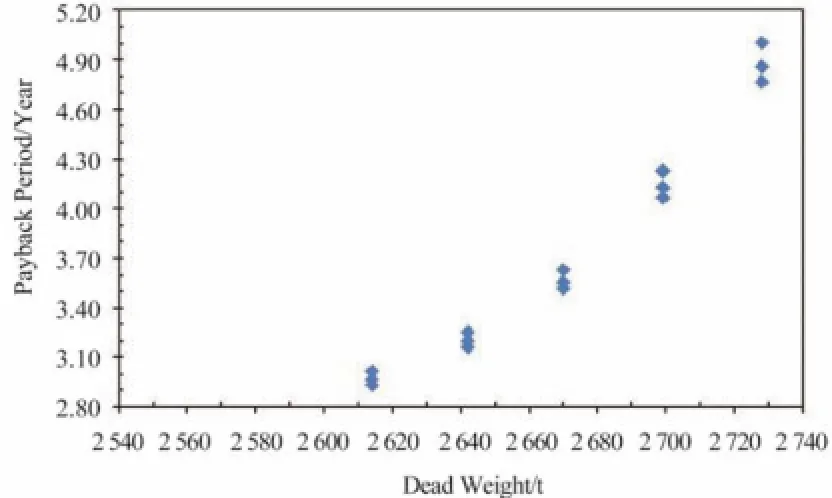
图2 投资回收期(PBP)分布Fig. 2 The distribution of PBP
4 敏感性分析
为进一步分析各个指标对所选船型方案的影响,有必要对其敏感性进行分析。将燃料价格、船价、运费等参数对船舶主要技术指标和经济指标的影响来分析其敏感性。为了尽量能够选择最佳的船型方案,参数的变化范围取 25%,20%,15%,10%和 5%,计算出在该变化范围内的最佳投资回收期 PBP 和净现值NPV,计算结果如图3 和图4 所示。
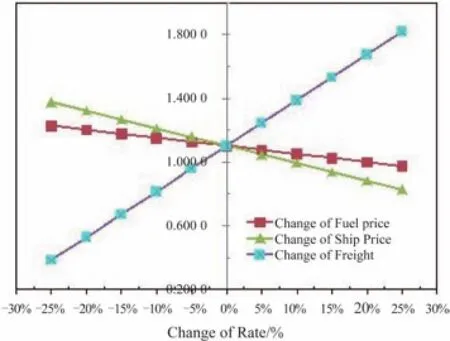
图3 投资回收期(PBP)的敏感性变化曲线Fig. 3 The sensibility analysis curve of PBP
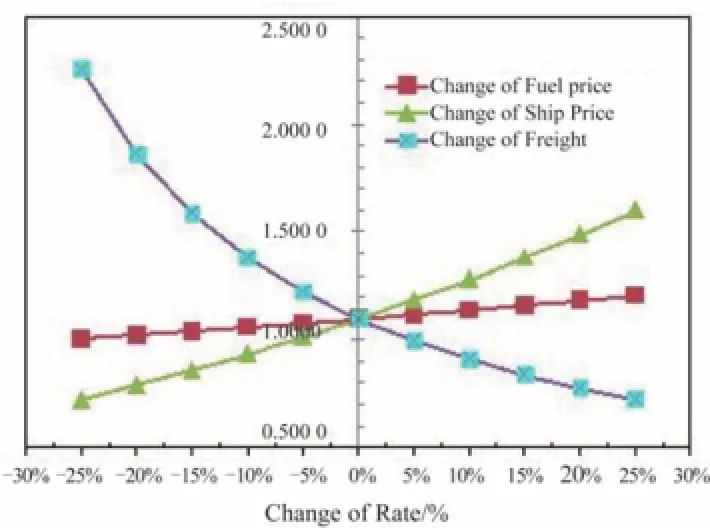
图4 净现值(NPV)的敏感性变化曲线Fig. 4 The sensibility analysis curve of NPV
5 结 语
本文采用层次分析法理论和变值法,提出了船舶船型技术经济性层次分析方法,建立起船舶船型经济评价的层次分析数学模型。通过对珠江干线 3 000 t 级散货船的船型进行实例研究分析,得出了船型优化综合评价指标的排序,得出综合最优船型。在此基础上,对影响船型方案的参数进行了敏感性分析。文章提出的船型方案层次分析的经济评价方法,对船型的优化设计具有理论研究和实用价值。
[1]杨路春, 李学斌, 丁明君, 等. 多目标遗传算法和决策在船型论证中的应用[J]. 哈尔滨工程大学学报, 2012, 33(12):1459-1464. YANG Lu-chun, LI Xue-bin, DING Ming-jun, et al. Application of multi-objective genetic algorithm and decision-making skills in ship form evaluation[J]. Journal of Harbin Engineering University, 2012, 32(12): 1459-1464.
[2]程红蓉, 刘晓东, 冯佰威. 多目标优化在船型设计中的应用研究[J]. 中国造船, 2014, 55(1): 76-82. CHENG Hong-rong, LIU Xiao-dong, FENG Bai-wei. Study on multidisciplinary optimization method for hull forms design[J]. Shipbuilding of China, 2014, 55(1): 76-82.
[3]陈雅菊. 基于多目标遗传算法和主成分分析的船型主尺度论证[J]. 船海工程, 2015, 44(2): 31-35. CHEN Ya-ju. Application of fast non-dominated sorted genetic algorithm and principle component analysis in ship main dimensions design[J]. Ship & Ocean Engineering, 2015, 44(2): 31-35.
[4]陈继红. 基于灰色关联的船型决策经济论证方法与应用[J].中国航海, 2012, 35(2): 102-105. CHEN Ji-hong. Method of economic evaluation for ship form development decision making based on gray relational theory and its application[J]. Navigation of China, 2012, 35(2):102-105.
[1]丁丽萍, 张晓晗. 必要费率在经济船型论证和方案比选中的应用[J]. 港工技术, 2014, 51(4): 63-65. DING Li-ping, ZHANG Xiao-han. Application of required rate in analysis of economical ship style and comparison of options[J]. Port Engineering Technology, 2014, 51(4): 63-65.
[2]李文龙, 谭家华. 基于最小偏差法的集装箱船船型优化[J].中国造船, 2002, 43(4): 1-5. LI Wen-long, TAN Jia-hua. Optimization of container ship principal parameters based on minimum-deviation method[J]. Shipbuilding of China, 2002, 43(4): 1-5.
[3]GUIN M M, KATO H, YAMAGUCHI H, et al. Reduction of skin friction by microbubbles and its relation with near-wall bubble concentration in a channel[J]. Journal of Marine Science and Technology, 1996, 1(5): 241-254.
[4]BESNARD E, SCHMITZ A, HEFAZI H, et al. Constructive neural networks and their application to ship multidisciplinary design optimization[J]. Journal of Ship research, 2007, 51(4):297-312.
[5]陈衍泰, 陈国宏, 李美娟. 综合评价方法分类及研究进展[J].管理科学学报, 2004, 7(2): 69-79. CHEN Yan-tai, CHEN Guo-hong, LI Mei-juan. Classification & research advancement of comprehensive evaluation methods[J]. Journal of Management Sciences in China, 2004, 7(2):69-79.
[6]刘寅东, 余秀丽, 苏绍娟. 西江干线集装箱船船型论证[J]. 船海工程, 2011, 40(2): 9-13. LIU Yin-dong, YU Xiu-li, SU Shao-juan. Technical and economic evaluation for the container ships in Xijiang river[J]. Ship & Ocean Engineering, 2011, 40(2): 9-13.
[7]SATTY T L. Applications of analytical hierarchies[J]. Mathematics and Computers in Simulation, 1979, 21(1): 1-20.
[8]SAATY T L. Modeling unstructured decision problems: a theory of analytical hierarchy[C]//Proceedings of the First International Conference on Mathematical Modeling. Rolla: University of Missoure Rolla, 1997, 1: 59-77.
[9]SATTY T L. The analytical hierarchy process[M]. New York:McGraw-Hill Company, 1980.
[10]桑松. 船型方案论证与智能决策方法研究[D]. 大连: 大连理工大学, 2002. SANG Song. Study on ship form evaluate alternatives and intelligent decision-making methods[D]. Dalian: Dalian University of Technology, 2002.
Research on the analytic hierarchy process model of ship optimization based on variable value method
CHEN Jian-ping1, 2, XU Jie3, GONG You1, HUANG Peng-ju1, XU Yan-min1
(1. School of Ship Engineering, Guangzhou Maritime Institute, Guangzhou 510725, China
2. School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiaotong University, Shanghai China 200240, China
3. Faculty of Automation, Guangdong University of Technology, Guangzhou 510006, China)
The paper presents the Analytic Hierarchy Process method of ship hull form technology and economy, and establishes a mathematical model for the economic evaluation of ship hull form by employing the theory of Analytic Hierarchy Process and variable value method. Based on the case study of the ship type of the 3 000 ton bulk cargo ship in the Pearl River main line, the paper obtains the sort of optimization comprehensive evaluation index, and obtains the comprehensive optimal ship form. On this basis, it studies the sensitivity analysis of the parameters effecting on the ship form scheme. The economic evaluation method of Analytic Hierarchy Process proposed has theoretical and practical value for the design and optimization of ship form optimization.
ship form optimization;analytic hierarchy process;variable value method;sensitivity analysis
U661.2
A
1672-7619(2016)05-0069-05
10.3404/j.issn.1672-7619.2016.05.015
2016-01-28;
2016-02-02
广东省交通科技计划资助项目(2015-02-050);中国博士后基金资助项目(2015M581622);广东省自然科学基金资助项目(2014A030313792)
陈建平(1973-),男,博士,副教授,主要从事船舶结构分析与船舶性能研究。
