傅立叶变换在数字信号处理中的应用研究

司新新 李佳

【摘要】 传统的信号分析和处理使用了傅立叶变换，这种数学工具可以处理非平稳信号的分析局限问题，有着非常重要的意义。本文立足于相关的理论基础，重点探讨了短时傅立叶变换的实现情况以及窗函数的选取，希望为后期的相关应用研究提供参考和建议。

【关键词】 不确定性原理 矩形窗 平移卷积 FFT

一、理论基础

作为一种传统数学工具，傅立叶变换在信号分析与处理方面有着较为重要的作用。傅立叶变换投入使用之后，就可以实现信号的时域和频域之间的自由变换[1]。有些确定信号的频谱并不会随着时间变化，还有一些平稳的随机信号，这些信号只要样本选取的较为合理，就会通过傅立叶的相关分析在满足一定条件后得到合适的结果。本文主要是立足于数字信号处理过程中，短时傅立叶变换是如何发挥作用的，最后使用Matlab 语言编程来了解相关的分析结果。

二、短时傅立叶变换的实现

（1）连续短时傅立叶变换的定义

假设：x（t）代表被分析信号，t=- ∞～∞，分析窗为w（t），那么就可以使用以下公式来解释非平稳信号x（t）的短时傅立叶变换。即：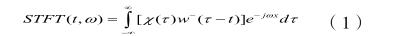

时间t 处短时傅立叶变换的计算也是按照了一个完整的过程展开的，具体情况如下：

1）获取w（τ-t）。把分析窗w（τ）由时间零处平移至时间t 的位置上，得到需要的结果；2）获取短时信号xi（τ）=x（τ）w（τ-t）。用水平方向移动过后的分析窗加窗截断相关的信号，获取需要的结果；3）分析结果。使用傅立叶变换分析短时信号xi（τ）的频谱。在这个过程当中，相关环节的实际需求是较为明显的，只要按照流程进行，就能得到相应的结果。如果，想要获取高分辨率，那么在分析窗的选择上要严格一些，时间短的分析窗比较符合标准。

（2）连续短时傅立叶变换的频域形式

傅立叶变换有着自己独特的性质，那么，两个时域信号乘积的傅立叶变换与各自频域的卷积相等，根据这个原理，（1）式也可以得到以下的结果：

式中窗函数在整个公式中有着自己独特的存在价值，主要是为了实现x（n）在n 时刻附近的一小段信号的处理，这种处理也是由傅立叶变换来完成的。窗函数的变化与n之间是相辅相成的，前者随着后者移动，从这个方面就可以得到相关的结论：信号频谱随着时间n的变化而变化。

2）从线性滤波的角度解释离散短时傅立叶变换

（4）短时傅立叶变换的时域、频域采样

短时傅立叶变换的ω作为一个变量，属于连续性的，在计算机开展相关的运算的时候，频域之间应该是离散化的。如果按照上述的解释，那么选取的所有的参数必须符合相关的频率采样定理。在窗口的位置上，每次移动的距离应该都是一样的，设定的数值为30。这就是一个与采样有关的问题。短时傅立叶变换的时间分辨率是非常有限的，因此，在选样方面要掌握好一个度，不然没法满足相应的需求，同样，采样的间隔也是要设置合理的。

三、窗函数的选取

1）不同的窗的选择。不同的窗有着各自独特的特点，因此应该按照实际的需求选择合适的窗。矩形窗主瓣宽度较窄，旁瓣峰值较大，旁瓣峰值衰减速度较慢，这些属性导致其容易泄露频谱，从而导致分析性能的弱化。汉宁窗和海明窗有着与矩形窗截然相反的属性，比较适合分析，因此，使用相关的分析方式时，能够取得较为优异的分析结果。实际上，最佳的分析窗正好是上面两者的结合，因此，在很多时候，具体的操作都是结合不同条件来选取最合适的分析窗函数的。2）不同的窗长度的选择。当分析窗函数确定了之后，也应该注意选择合适的分析窗长度。当窗口过于长的时候，信号不是很平稳的话，那么傅立叶变换的价值就会较小，运算量就会很大；相反，窗口过小，那么摄取的信息量又会太小。因此，要想获取精确的结果，务必要选择合适的窗函数的长度。

结束语：傅立叶变换在分析时变信号和非平稳信号方面有着自己的局限，而短时傅立叶则刚好可以解决这些问题，但是也并非没有任何缺陷。另外，窗函数的长度也是必须要合适的，这样才能确保短时信号处于较为稳定的状态，进而得到比较精确的分析结果。

参 考 文 献

[1]王金婵，赵永安.分数傅立叶变换的进展与展望[J].应用光学，2003（5）：57.

[2]朱全银，邓建平.基于分数阶傅里叶变换的线性调频干扰抑制[J].探测与控制学报，2009（1）：1014.

[3]窦德召，常鸿森，林睿.变形分数傅立叶变换相关器[J].华南师范大学学报：自然科学版，2005（3）：7079.