基于数字全息层析的三维测量技术

徐强胜高瑞翔房鹤飞周文静于瀛洁/ .上海市质量监督检验技术研究院；.上海大学

基于数字全息层析的三维测量技术

徐强胜1高瑞翔1房鹤飞1周文静2于瀛洁2/ 1.上海市质量监督检验技术研究院；2.上海大学

针对传统测量方法不能同时实现功能性梯度材料外部三维轮廓测量和内部三维结构测量的缺陷，提出了基于数字全息层析的三维测量技术。以单模光纤作为实验样本，采用基于数字全息层析的三维测量技术对其进行分析。实验结果表明，基于数字全息层析技术的三维结构测量方法能很好地实现功能性梯度材料等一些透明物体的三维轮廓测量和内部三维结构测量。

数字全息层析技术；数字全息技术；计算机断层成像技术；三维测量

0　引言

随着科技的发展，人们对物质的分析已经从物体表面深入到物体内部，从物体的二维发展到物体的三维。特别是针对一些功能性梯度材料（如光纤、梯度折射率透镜、棒透镜等）及活体细胞，不仅需要测量其外部三维轮廓，同时由于内部物质不同，其内部折射率也不同，因此也需要测量其内部三维结构。但传统的测量技术，如轮廓测量仪、三坐标测量仪、CT测量机、白光干涉仪和干涉仪等，都不能同时实现外部轮廓和内部结构的测量。因此，如何测量功能性梯度材料的外部三维轮廓及内部三维结构成为当前研究的热点。

数字全息层析［1］是一项光学层析成像技术［2］，是数字全息技术［3-4］与层析（CT）技术［5-7］的融合体。数字全息技术采用非接触测量方法实现被测物的三维波前测量。但波前仅表现为均匀物体的三维轮廓或物体内部折射率的平均值，无法实现内部结构测量。而CT技术具有较好的三维重建算法，能实现被测物体外围轮廓和内部结构的三维重构，因此它被用于物体的三维重建上。将数字全息技术与层析技术相结合，能实现三维轮廓及内部三维结构的测量。该方法能为工业检测、生物医学研究提供更为有效的技术工具。

本文首先介绍数字全息层析技术的基本原理［8］，继而提出实验方案。以光纤作为被测对象，实现对被测物的内部折射率分布测量和外部三维轮廓测量。

1　数字全息层析的基本原理

数字全息层析技术的核心是数字全息原理［9］和CT重构原理［10］。它的三维重建是由以下两个步骤组成的：

1）数字全息图的记录及再现过程。即先通过数字全息的方法记录被测物在多个方向上的全息图，然后采用傅里叶变换等方法对其进行数字再现。

2）采用CT算法进行三维重建过程。以数字全息再现得到的数据为源数据，然后采用代数迭代法进行CT重建。

1.1数字全息的记录与再现过程

数字全息技术是使用干涉方法在全息面上记录物波的全部信息（振幅和位相）。这一信息存在于物平面和全息面之间光波经过的任一平面上。在这些平面上能够记录携带物体全部信息的波前，此过程为波前记录过程。在一定条件下再现物光波的波前，从效果上看，相当于在记录时被“冻结”在记录介质上的波前从全息图上“释放”出来，然后继续向前传播，以产生一个可观察的三维像，此过程为波前再现过程。数字全息的记录与再现过程可简单描述为干涉记录，衍射再现。

图1为全息记录及其再现的典型示意图。图中d为全息图的记录距离，d'为全息图的再现距离（d'在数值上等于d或-d）。（x，y）为物平面，（ξ，η）为全息平面，（x'，y'）为再现平面，O（ξ，η）为全息面上的物波信息，r（ξ，η）为再现光波（因再现光波C（ξ，η）常取原记录参考光波r（ξ，η），故通常直接用r（ξ，η）表示再现光波），b（x'，y'）为再现平面上的物波信息，并设照射记录物体的光波波长、记录参考光波波长和再现光波波长均为λ。

图1　全息记录与全息再现的空间坐标关系

其中，全息面上物光与参考光之间的干涉强度信号表达式为

对于数字全息而言，由于采用CCD记录该干涉强度，设CCD有效靶面的长度和宽度分别为L、W；像素数分别为M、N；所以CCD采集到的全息图为

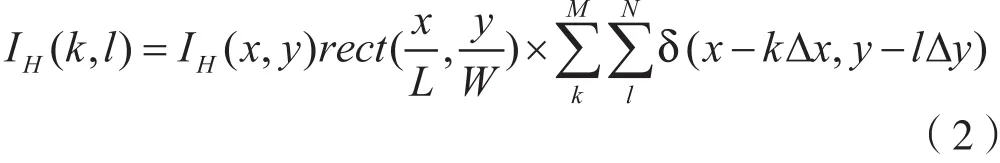
全息图的再现是用原来的参考光或参考光的共轭光照射全息图得到的，也就是再现光受到全息图的调制获得物信息或物共轭信息。根据采用的再现光类型，全息再现可分为透射式与反射式。当用再现光照射全息图时，得到光场的分布为

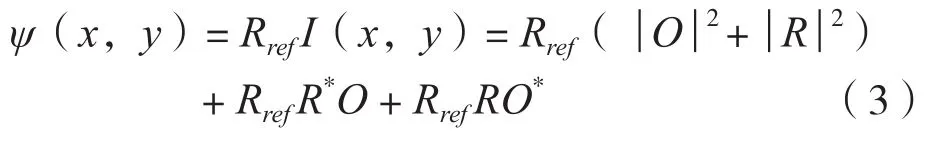
式中：第一、二项对应的是零级；

第三、四项分别对应物信息和物共轭信息当Rref= R时，第三项变为│R│2O，如此可以得到物信息。再现光也可以是原来参考光的共轭光，即Rref= R*，此时式中的第四项变为│R│2O*，因此可以再现出物信息的共轭。

因而全息技术能通过记录的全息图再现出物体的三维强度及相位信息，但它获得的是被测物体波前三维轮廓分布，并不包含被测物内部结构信息。

1.2CT的三维重建过程

CT的基本原理是投影重建原理，即通过不同方向上的投影图来重建出物体的原始图像，图2为CT的工作原理示意图［11］。

图2　CT工作原理示意图

当一束射线穿过物质并与物质相互作用后，射线强度将受到射线路径上物质的吸收或散射而衰减，如图3所示。衰减规律遵循比尔定律。用衰减系数度量衰减程度，设物质为非均匀的，一个面上衰减系数分布为μ（x，y），当射线穿过该物质面，入射强度I0的射线经过衰减后以强度I穿出，射线在面内的路径长度为L，由比尔定律确定的I0、I和μ（x，y）的关系如下：

图3　射线穿越衰减系数为μ（x，y）、长度为L的物体

由于直线L的法线式方程为xcosθ + ysinθ = s，式（5）等号左边积分值的积分路径完全由θ和s来决定，因此可记为

称p（s，θ）为射线穿过物体后的投影值，也就是通常所说的射束和。由式（6）可以看出，投影值p（s，θ）是被检物体某断面的线性衰减系数分布函数μ（x，y）沿射线路径的线积分值。变动θ和s可得到各个方向、不同位置上的投影值，然后通过采集到的一系列投影值p（s，θ）来反求线性衰减系数分布函数μ（x，y），而衰减系数与折射率是相关的，因此也就能由投影来重建出原图像［12］。

2　测量方案

本文选取了轴对称的光纤作为被测对象，其出厂值特征为：横截面直径125 μm，横截面折射率呈渐变形。

2.1数字全息采集及重建方案

采用马赫-曾德干涉系统［13］来实现样本全息图的采集，如图4所示。由于光纤的直径较小，因此采用数字显微全息光学记录的方式进行记录，以扩大光纤记录尺寸。在采集过程中，每旋转光纤60°记录一幅数字全息图，如图5（a）所示。该实验系统较简洁，这有效提高了层析重建的快捷性和有效性。

采用卷积再现算法对全息图进行全息再现，得到的结果如图5（b）所示。

图4　实验方案

图5　（a）数字全息图；（b）全息重建相位图

2.1层析重建方案

1）首先沿x轴方向提取其中一个截面的位相图，每个方向上有71个投影射线，每条投影射线的宽度为2.84 μm，获得光纤断面四向（0°、60°、120°、180°）投影数据，如图6所示。

图6　光纤断面四向投影数据

2）以图6所示的投影图作为层析重建的数据采用代数迭代法对投影数据进行迭代重建，得到该截面的位相差分布图。由于采样像素间隔与投影射，线的宽度相同，即为2.84 μm，因此重建得到的各个像素的大小为2.84 μm×2.84 μm，同时假设同一个像素内的折射率值相同，则根据位相差与折射率的关系可计算出各个像素的折射率，其公式为）

式中：Δφi—— 第i个像素的位相差；

λ —— 波长；

ni—— 第i个像素的折射率；

n0—— 空气的折射率，n0= 1；

Δl —— 单位像素宽度

图7　（a）光纤纤芯内部折射率重建结果；（b）层析重建光纤断面横向三维折射率分布

根据位相图的层析重建结果，可求出光纤内部结构折射率分布图，其结果如图7所示。

将每层重建的光纤内部折射率按初始方向三维叠加建模，获得了光纤的三维轮廓结果，如图8所示。

通过对数字全息层析重建获得了光纤的内部结构折射率分布图及三维结构图的分析，其测量结果符合光纤的实际分布。

图8　光纤三维轮廓图

5　结语

本文开展了基于数字全息层析技术的三维结构测量技术的实验分析。实验结果表明，基于数字全息层析技术的三维结构测量方法能很好地实现功能性梯度材料等一些透明物体的三维轮廓测量和内部三维结构测量。

［1］ Satos， Kunmakara T. Measurement of temperature in a flame by holographic interferometers and CT technique ［J］. Prepe Book 24th Combust Symp （in Japan），1986（6）：16.

［2］ F Charrière， N Pavillon， T Colomb， et al.. Living specimen tomography by digital holographic microscopy： morphometry of testate amoeba ［J］. Optics Express， 2006，14 （16）：7005-7013.

［3］ Ulf Schnars and Werner P O Juptner. Digital recording and numerical reconstruction of holograms ［J］. Meas. Sci. Technol，2002 （13）：85-101.

［4］ 郁道银，谈恒英.工程光学［M］.北京：机械工业出版社， 2001.

［5］ Henrie Turbell. Cone-Beam Reconstruction using Filtered Back projection ［D］. Sweden： LinkoPing University， 2001.

［6］ 庄天戈.CT原理与算法［M］.上海：上海交通大学出版社， 1992.

［7］ 周文静，徐强胜，于瀛洁. 基于三投影方向的层析重建分析［J］. 光子学报，2010，39（7）：1257-1262.

［8］ 周文静，胡文涛，郭路，等. 少量投影数字全息层析重建实验研究［J］.物理学报，59（12）：8499-8511.

［9］ Pia Massatsch， Florian Charrière， and Etienne Cuche， et al.. Timedomain optical coherence tomography with digital holography microscopy ［J］. Applied Optics， 2005， 44（10）：1807-1812.

［10］ KAKA， S LANEYM. Principles of computerized tomography imaging ［M］. New York： IEEE Press， 1988.

［11］ LI Hui， WAN Xiong， LIU Tao-li， et al. A computed tomography reconstruction algorithm based on multipurpose optimal criterion and simulated annealing theory［J］， Chinese Optics Lerrers，2007.5（6）：340-343.

［12］ 张顺利，张定华，熬波，等.不完全投影数据图像重建的ART算法研究［J］.计算机工程与应用，2007， 43（10）：8-10.

［13］ Zhou W J，Xu Q S，Yu Y J，Asundi A. Opt.Laser Eng ［J］. 2009，47（9）：896-901.

3-D measurement technique based on digital holographic tomography

Xu Qiangsheng1，Gao Ruixiang1，Fang Hefei1，Zhou Wenjin2，Yu Yingjie2
（1. Shanghai Institute of Quality Inspection and Technical Research； 2. Shanghai University）

The traditional measurement methods can not simultaneously measure the external 3-D profle and internal 3-D structure of functional gradient materials. In this paper， the 3-D measurement technique based on digital holographic tomography is proposed， and is used to analyze a single-mode fber as an experimental sample. Experimental results show that the digital holography tomography can well achieve the external 3-D profle measurement and internal 3-D structure measurement of functional gradient materials and other transparent objects.

digital holography tomography； digital holography；tomography； 3-D measurement