基于排队系统的最佳拥塞控制比例研究

周驰岷，郭　兵，沈　艳，邓立国

（1.四川大学 计算机学院，四川 成都　610065；2.四川广播电视大学 信息技术中心，四川 成都　610073；3.成都信息工程大学 控制工程学院，四川 成都　610225；4.沈阳师范大学 教育技术学院，辽宁 沈阳　110034）

基于排队系统的最佳拥塞控制比例研究

周驰岷1，2，郭兵1，沈艳3，邓立国4

（1.四川大学 计算机学院，四川 成都610065；2.四川广播电视大学 信息技术中心，四川 成都610073；3.成都信息工程大学 控制工程学院，四川 成都610225；4.沈阳师范大学 教育技术学院，辽宁 沈阳110034）

对控制报文和网络拥塞间的平衡问题进行研究。通过一个单服务队列模型来描述拥塞控制策略，利用排队系统中的马尔可夫过程，提出一种两阈值的流量控制算法使其控制报文速率能满足最好的拥塞概率。通过分析发现排队系统中拥塞概率随缓冲区大小变化发生指数衰变，并定义该衰变指数为大偏差指数用来描述控制报文与拥塞概率间的比例。最后通过带宽共享模型，模拟并分析不同带宽情况下控制报文与拥塞概率间的最佳比例及其大偏差指数。

控制报文和网络拥塞间的平衡；两阈值流量控制算法；拥塞控制；马尔可夫过程；排队系统

拥塞控制是排队系统的一个重要组成部分，缓解网络拥塞的基本方式有两种［1］：流量控制和资源分配。其中流量控制是根据队列的拥挤程度控制进入队列报文的速率，而资源分配是为拥堵的队列提供更多的服务［2］。在传输控制协议（TCP）网络中，缓冲区即将溢出时会丢弃数据包，这会导致窗口的大小和报文到达速率的减小［3］。像随机早期检测（RED）这样的主动队列管理算法即是通过在缓冲区达到溢出限制之前随机丢弃一些报文来主动避免拥堵［4⁃5］。

如果流量控制器能获得系统中非常准确的拥塞信息，那么即可通过调整输入速率实现非常有效的拥塞控制。然而获得准确的队列长度需要传送大量的控制信息，此外在TCP这样的系统机制下也经常会发生意外的报文丢弃［6⁃7］。

1　系统模型

1.1系统说明

首先假设一个用于描述拥塞控制的简单队列模型。图1是具有恒定服务速率β的单服务器队列，观察队列的变化并发送控制报文给流量控制器从而改变输入速率S（t）。为了简化分析，假设任意时刻的输入速率是两个泊松分布中的一个，即S（t）∈｛α1，α2｝，其中α2＜α1，α2＜β。

图1　单服务器队列

1.2吞吐量、拥塞概率、输入速率

在拥塞控制策略的设计中，吞吐量、拥塞概率、输入速率是三个关键参数，通常希望平衡吞吐量与拥塞概率，既能保证足够高的吞吐量又能有效地控制拥塞［8］。本文中假设能够满足一个最小吞吐量，当最小吞吐量α2为min（α1，β）时，则最小吞吐量是通过提高输入速率α1并兼顾拥塞概率来实现的。首先考虑一个单阈值流控策略，当队列长度小于等于阈值m时采用较高的输入速率α1，当大于m时则采用更低的输入速率，这表明m较大时吞吐量更大，反之亦然。因此，给定最小吞吐量要求时，就可以确定对应的阈值，这表明一旦阈值确定，单阈值流控策略能减少拥塞发生的概率。然而，由于需要频繁发送控制信息，该系统可能在m和m+1之间波动。因此将单阈值流控策略扩展，使其能提供更大的控制灵活性，并保证吞吐量和良好的拥塞控制性能。

2　两阈值流控策略

两阈值流控策略的输入速率在两个不同的阈值m 和n间切换，其中n≥m+1，而m是通过最小吞吐量确定的。初始情况下，当队列长度小于n时以输入速率α1运行，当队列长度超过n后，切换到较低输入速率α2，直到队列长度重新小于m后，输入速率又切换为α1。

假设Q（t）表示时间t的队列长度，且输入速率S（t）∈｛α1，α2｝。定义Y（t）=（Q（t），S（t））表示时间t的系统状态，显而易见在两阈值流控策略中，Y（t）是一个连续时间的马尔可夫过程［9⁃10］，如图2所示。

图2　两阈值流控策略对应的马尔可夫过程Y（t）

定义k=n-m为两个队列长度阈值之间的差值，使用m+i（1）和m+i（2）分别表示状态（Q（t）=m+i，S（t）=α1）和（Q（t）=m+i，S（t）=α2），i=1，2，…，k-1。对于长度小于m或大于n的队列，输入速率只能分别是α1和α2。注意，当k=1时相当于单阈值流控策略，当k＞1时两阈值流控策略的吞吐量不会比单阈值时更小，此时单阈值为m的流控策略同样能满足k＞1时两阈值流控策略的要求。

2.1拥塞概率和输入速率

在此定义ρ2=α2β，ρ1=α1β，且η2=1ρ1，则ρ2＜1，ρ1＞ρ2。用pj表示图中的稳态概率，当j≤m或j≥n时，用表示状态m+i（1（）m+i（2））的稳态概率，其中i=1， 2，…，k-1，通过求解不同的稳态概率pm，发现：

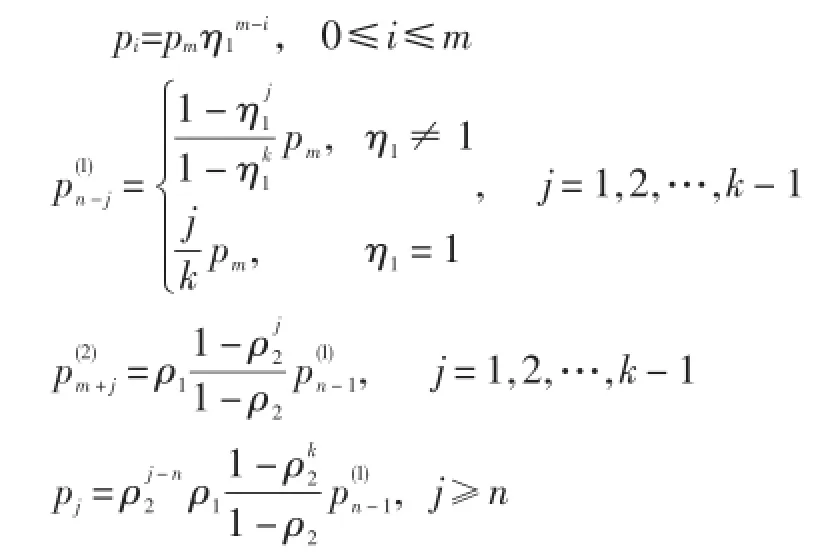
未知值pm可以通过概率归一来确定：

通过上面导出的稳态概率，可求得拥塞概率：

状态从n-1（1）变化到n或从m+1（2）变化到m，则每秒控制报文速率：

由式（2）、式（3）可知k决定了拥塞概率和输入速率之间的平衡性，当k较大时输入速率较小而概率拥塞较大，反之亦然。在两阈值流控策略中，m决定了最小吞吐量，而k决定了拥塞概率和输入速率之间的平衡性。

2.2大偏差指数

在很多排队系统中，拥塞概率随缓冲区大小M变化发生指数衰变。当缓冲区变大时，指数项在决定衰变概率的过程中起决定作用。因此只需考虑衰变指数，而忽略缓冲区M对拥塞概率的其他影响，这就是所谓的大偏差指数。对特定的流控策略，定义其拥塞概率衰变的大偏差指数为：

当Q≤m时，M-m越来越大。

由式（3），输入速率可以任意小，若k（M）趋于无穷大。则k（M）随M线性增长为无穷大，那么大偏差指数为常量，即-ln ρ2。当k变大时，拥塞概率增大，然而它仅在缓冲区内线性增长，因此大偏差指数保持不变。大家只对大偏差指数与拥塞概率的相对变化感兴趣，而不是它的实际值，定理1确定了两阈值流控策略具有最优大偏差指数。

定理1两阈值流控策略在任意输入速率的所有流控策略中可能具有最好的大偏差指数。

能得到这个结论是由于在较低的输入速率α2的情况下，两阈值流控策略和M/M/1队列的大偏差指数相同，且优于任何流控策略。

2.3两阈值流控策略和随机早期检测

即便在缓冲区并未溢出的情况下，随机早期检测也会随机丢弃数据报文来防止拥塞。考虑两个队列长度阈值m和n，其中n＞m。如果队列长度不超过m，无论什么输入速率也无报文被丢弃；而队列长度达到或超过m，则报文总是被丢弃，并且会导致输入速率降低。如果队列长度在m和n-1之间，报文以概率q随机丢弃。而两阈值流控策略非常类似于上述随机早期检测的算法，如图3所示。

图3　随机早期检测算法对应的马尔可夫过程

对于队列长度小于或等于m时，总是有较高的输入速率；如果队列长度增大到n且输入速率是α1，会触发拥塞通知，输入速率被降到α2；若输入速率为α1且队列长度在m～n-1之间，则以概率q发送拥塞通知，并将输入速率降低到α2。图3是这种策略对应的马尔可夫过程。

可以通过分析图3中的马尔可夫链得到拥塞概率和拥塞通知间的平衡性，在保证最小吞吐量的条件下一旦确定了阈值m，则输入速率和拥塞概率间的平衡就由q和n来确定。此外，当队列长度大于n时输入速率降低为α2，这也实现了拥塞概率为ln（1ρ2）的最优大偏差指数。事实上，两阈值流控策略也可用于模拟实际的队列管理算法，如随机早期检测算法。

3　控制信号的带宽分配优化

虽然控制信号消耗的带宽不大，但是在无线网络的情况下，不可能发送任意量的控制信号而不牺牲带宽。通常需要发送控制信号纠正错误，但这样也会降低可用服务带宽。因此建立一个模型来描述服务速率和控制信号间的平衡关系，从而确定最好的拥塞概率衰变指数下的最优控制信号带宽分配。

3.1带宽共享模型

假设队列服务速率与控制报文重传次数d-1成线性递减，即：

式中：β是无冗余控制报文（d=1）时的服务速率；控制信号所占带宽与报文重传次数d-1成正比；每个控制报文所占带宽为1/Φ，其中，Φ＞0，为常量。

3.2用于控制报文的最优带宽

给定的系统参数ρ1，ρ2，Φ，以及控制误差δ∈［0，1），求解使拥塞概率的大偏差指数最大的最优带宽比f（*δ）。定义：

类似β（f）的定义，在此定义：

为保持队列稳定，需要比α2大的输入速率，因此α2＜β［1-f］或f＜1-ρ2。接着计算大偏差指数对应的错误概率δ及控制带宽比f。

命题2：对任意δ∈［0，1］，f∈［0，1-ρ2），对应的大偏差指数：

定义2对任意给定的δ∈［0，1），最佳比例f（*δ）是式（7）中的E（δ，f）：

由于1/Φ表示每个重复报文所占带宽，因此Φ决定了用于控制的最优带宽。Φ有三种不同的情况确定最佳带宽比例f（*δ），Φ≤Φ1；Φ≥Φ2；Φ1＜Φ＜Φ2，其中：

Φ的值由ρ1和ρ2确定，当ρ1≤1时，Φ≥Φ1不存在，即使Φ任意大仍然会存在Φ1＜Φ＜Φ2。下述定理给出了三种不同Φ的最佳带宽比f（*δ）。

定理2对于给定的ρ1和ρ2，最佳带宽比 f*（δ）根据Φ的值分别为：

（1）Φ≤Φ1时，f*（δ）=0，δ∈（0，1）。

（2）Φ≥Φ2时，

的惟一解。

（3）Φ1＜Φ＜Φ2时，存在δ′和δ″且δ*＜δ′＜δ″＜1使：

在（0，1-ρ2）中的惟一解。

3.3最优解讨论

（1）错误概率小于δ*：f（*δ）=0，δ∈［0，δ*］，大偏差指数的最大值为-ln ρ2且任何控制冗余不会产生叠加。

（2）Φ≤Φ1时：拥塞概率的最佳大偏差指数可以通过发送控制报文调整输入速率来获得，然而比错误概率的增加更糟糕的是增加控制报文会挤占带宽。

（3）Φ≥Φ2时：当δ＞δ*时，由式（10）差错概率为 δΦf+1时取得最佳比例f（*δ）。若ρ1=1.2，ρ2=0.3，Φ=10，图4中实线给出了δ对应的f值；图5中实线给出了最佳大偏差指数的值

图4　Φ较大时的最佳比例

图5　Φ较大时的最佳大偏差指数

（4）Φ1＜Φ＜Φ2时：当δ＞δ*时，如图6所示最佳比例沿曲线增加，当到达特定错误概率δ′时的最佳比例开始急剧下降并在错误概率为δ″时达到零值，式（11）说明当δ在（δ′，δ″）时取得最佳比例，其对应的最佳大偏差指数如图7所示。

图6　中等大小Φ的最佳比例

图7　中等大小Φ的最佳大偏差指数

4　结论

本文的目的是研究控制速率和拥塞控制策略间的平衡关系，即研究控制报文发送频率对拥塞控制效果的影响。由于很难在实际网络中对这种平衡进行研究，因此构建了一个单一服务队列的简单的模型来进行分析。研究发现，可以通过一个简单的带宽共享模型的控制信号确定最佳错误保护量，不同于无误差的系统，当差错概率大于临界值时，该系统带宽的很大比例会被控制报文占用。同时，必须考虑控制报文消耗的带宽及其可能对拥塞控制的影响。

［1］任丰原，林闯，刘卫东.IP网络中的拥塞控制［J］.计算机学报，2003，26（9）：1025⁃1034.

［2］任立勇，卢显良.Internet拥塞控制研究［J］.电子科技大学学报，2002，31（1）：48⁃52.

［3］XU Changbiao，LONG Keping，YANG Shizhong.Allocating network resources by weight between TCP traffics［J］.Journal of computer science and technology，2003，18（2）：247⁃251.

［4］LAMA S S，WONGB J W.Queueing network models of packet switching networks part 2：Networks with population size con⁃ straints［J］.Performance evaluation，1982，2（3）：161⁃180.

［5］TAN Liansheng，PUGHB A C，MIN Yina.Rate⁃based congestion control in atm switching networks using a recursive digital filter ［J］.Control engineering practice，2003，11（10）：1171⁃1181.

［6］肖蕾，吴捷.大时延对拥塞控制系统性能的影响及补偿方法［J］.计算机测量与控制，2005，13（12）：1416⁃1418.

［7］李晓宇，戴航，张慧翔，等.Internet拥塞控制系统校正控制器的一种新的设计方法［J］.计算机测量与控制，2011，19（8）：1919⁃1921.

［8］江菊花，孙金生.自适应PD主动队列管理算法［J］.中南大学学报（自然科学版），2013（s2）：188⁃194.

［9］赖峻，张广驰.基于延迟探测机制的网关队列管理算法［J］.系统工程与电子技术，2014（4）：764⁃768.

［10］田波，杨宜民，蔡述庭.基于半马尔科夫决策过程的视频传输拥塞控制算法［J］.通信学报，2014，35（8）：154⁃161.

Research on optimal proportion of congestion control based on queuing system

ZHOU Chimin1，2，GUO Bing2，SHEN Yan3，DENG Liguo4
（1.College of Computer Science，Sichuan University，Chengdu 610065，China；2.Information Technology Center，Sichuan Radio and TV University，Chengdu 610073，China；3.Control Engineering College，Chengdu University of Information Technology，Chengdu 610225，China；4.College of Education Technology，Shenyang Normal University，Shenyang 110034，China）

The balance between control message and network congestion control is studied.The congestion control strategy is described with a single service queue model.A two⁃threshold flow control algorithm is put forward by utilizing Markov pro⁃cess to make the control message rate satisfy the optimal congestion probability.It is found by analysis that the congestion proba⁃bility occurs exponential disintegration with the buffer size，which is defined as the large deviation index to describe the ratio of control message and congestion probability.The ratio and large deviation index in different bandwidth are simulated and ana⁃lyzed with bandwidth sharing model.

balance between control message and network congestion control；two⁃threshold flow control algorithm；conges⁃tion control；Markov process；queuing system

TN911⁃34；TP393

A

1004⁃373X（2016）12⁃0014⁃04

10.16652/j.issn.1004⁃373x.2016.12.004

2015⁃11⁃13 基金项目：国家自然科学基金重点项目（61332001）；国家自然科学基金项目（61272104）；四川省教育厅科研项目（16ZB0102）；四川电大科研课题重点项目（KTGCJS2016002Z）

周驰岷（1975—），男，四川成都人，讲师，硕士。主要研究方向为计算机网络应用。郭兵（1970—），男，四川成都人，教授，博士。主要研究方向为嵌入式实时系统、软件工程、绿色计算等。沈艳（1973—），女，四川成都人，教授，博士。主要研究方向为计算机测量。邓立国（1972—），男，辽宁沈阳人，副教授，博士。主要研究方向为计算机模式识别。