基于马尔科夫链和贝叶斯网络的钻井风险预测

钟仪华 刘雨鑫 林旭旭

西南石油大学理学院

基于马尔科夫链和贝叶斯网络的钻井风险预测

钟仪华 刘雨鑫 林旭旭

西南石油大学理学院

钻井作业是高风险高投资的过程，这个过程中存在许多可能导致重大钻井事故的不确定因素，对此类不确定性因素进行预测进而达到预警或控制的目的，提前做好风险预防或降低风险损失具有较大的经济意义。通过研究钻井风险预测、马尔科夫链和贝叶斯网络方法，根据现场采用的指标体系，提出融合马尔科夫链和贝叶斯网络的钻井风险预测新方法。该方法可从纵、横两方面预测钻井事故的风险、弥补单独用马尔科夫链处理上层指标数据欠缺的不足；并可为诊断、监测和控制风险提供理论依据。实例研究表明，该方法是正确和可行的，用马尔科夫链进行纵向预测与实际的吻合度为82%，而贝叶斯网络仅为46%，融合后的方法优于现有方法。

钻井风险；风险预测；马尔科夫链；贝叶斯网络

钻井风险预测可避免或减少钻井事故。近年来，石油和数学领域的许多专家分别利用贝叶斯网络、模糊综合评价、蝴蝶结与模型模拟等方法研究了钻井风险问题，主要集中在对风险的定性和定量描

1　钻井风险预测

Drilling risk prediction

1.1钻井风险及其影响因素

Drilling risk and its influential factors

钻井风险是指在油气井钻井过程中存在的一切对钻井作业有影响的风险因素，主要包括操作人员疏忽、设备仪器故障、自然灾害及各种潜在因素，这些因素都可能对施工人员的安全、设备安全、生态环境等造成不同程度、不同形式的影响和危害［13］。

1.2钻井风险预测指标体系

Drilling risk prediction index system

根据钻井风险管理实际和文献调研结果，可将钻井风险预测的指标体系分为人的因素和物的因素2个1层指标，针对2个1层指标进一步设置11个2层指标和30个3层指标。以研究物的不安全因素说明对钻井作业的影响。物的不安全因素包括4个2层指标和11个3层指标：（1）安全防护缺陷：a.安全防护设施缺失，b.安全防护设施失效；（2）设备设施缺陷：c.一般设备缺陷，d.电器设备缺陷，e.井控设备缺陷，f.特种设备缺陷，g.消防设施缺陷；（3）钻井作业场所不良：h.自然条件不备，i.场所不符合要求；（4）自然环境不良：j.天气恶劣，k.自然灾害［6，14-16］。

2　基于控制的钻井风险预测新方法

A new drilling risk prediction method

based on risk control

2.1马尔科夫链预测方法

Prediction method of Markov chain

方程（1）就是C-K方程，是计算K步概率转移矩阵的依据［19］。马尔科夫链预测的方法步骤如下：（1）检验数据是否具有马尔科夫性，若有转步骤（2）；（2）计算每个指标的转移概率矩阵并建立预测模型；（3）选取初始状态进行预测；（4）结果与误差分析。

2.2贝叶斯网络预测方法

Prediction method of Bayesian network

贝叶斯网络是由变量节点和连接这些节点的有向边构成的一个有向无环图。节点表示随机变量，节点间的有向边表示节点间的相互关系（由父节点指向其子节点），用条件概率表达其关系强度。运用贝叶斯网络进行风险预测的目标在于网络推理，所以依据实际数据建立网络结构与训练网络参数是模型最重要的部分［20］。贝叶斯网络预测的步骤为：（1）贝叶斯网络结构学习；（2）贝叶斯网络参数学习；（3）贝叶斯网络推理。

2.3马尔科夫链和贝叶斯网络融合的预测方法

New prediction method integrating Markov chain and Bayesian network

2.3.1基本思想及方法步骤 马尔科夫链是探索由样本决定的在未来时间里变量的概率分布，是一种纵向预测的方法。贝叶斯网络则展示出指标之间的相互影响关系，是一种横向预测方法。结合这2种方法可以解决多层指标体系的非底层指标数据缺乏的问题，以实现宏观意义上的风险预测。贝叶斯网络在诊断方面的特点也为风险控制提供了基础。总的思路是用2种方法分阶段进行预测。新方法预测的步骤为：（1）检验随机过程是否为马尔科夫链，若是转（2）；（2）建立贝叶斯网络；（3）选取初始状态，用马尔科夫链预测；（4）将预测结果作为证据输入贝叶斯网络；（5）进行贝叶斯网络推理及预测。

2.3.2新方法的优势 马尔科夫链是基于时间的纵向预测方法；贝叶斯网络着眼于变量之间的相互影响。将2种方法融合，能够解决分层指标体系中上层指标数据缺乏的问题。如前面提出的指标体系共分3层，第1、2层指标为第3层指标的祖先节点，能够采集到的数据仅包含第3层节点的状态，缺乏第1、2层指标数据。仅使用马尔科夫链则不能对上层指标的风险进行直接预测；仅使用贝叶斯网络，对于低层指标来说，预测结果是对现有数据的古典概型统计结果。融合后的方法首先采用马尔科夫链针对第3层指标a，b，……，j，k进行预测，将该预测结果作为证据输入贝叶斯网络，预测上层指标风险发生的可能性。纵横结合，运用贝叶斯网络的优点弥补了马尔科夫链不能对缺乏数据的上层指标进行预测这一缺陷；另一方面也运用马尔科夫链的优点避免了将贝叶斯网络的参数学习结果粗糙地作为第3层指标a，b，……，j，k的预测值。

3　钻井风险预测实例与模型检验

Case study and model test on drilling risk prediction

以某井场2011年1月1日至2012年8月26日采集到的数据为例。表1中底层指标体系为指标a，b，……，j，k构成的集合；上层指标与底层指标的关系由序号标明，如a-b表示安全防护缺陷与其下层指标安全防护设施缺失a和安全防护设施失效b的关系。在贝叶斯网络模型中，指标节点a-b是其子节点a与b两个原因指标共同作用的结果，其他关系以此类推；这种关系通过手工方式融入到贝叶斯网络模型中。

表1　整理后的部分原始数据Table 1 Some processed original data

3.1马尔科夫链预测

Prediction by Markov chain

3.1.1“马氏性”检验 除j，k两指标外的其他指标并非0-1变量，以样本的四分位点为准将其离散化为4个级别即：极低、低、中、高，现场作业要依据实际情况和经验来划定分级标准。根据原始数据计算概率转移矩阵

构造统计量X2以检验数据是否具有“马氏性”

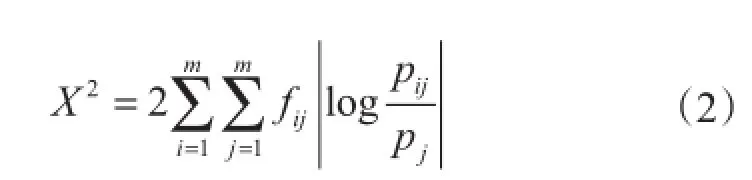
计算可得： X2（a）=119.2，X2（b）=119.1，X2（c）=136.0，X2（d）=104.4，X2（e）=99.9，X2（f）=91.5，X2（g）=141.5，X2（h）=135.2，X2（i）=61.5，取显著性水平α=0.05，则。可以看出，各指标的值都大于16.92，所以这9个指标均具有马尔科夫性。

由于j，k 指标具有较高破坏性和较强破坏力，如泥石流，只要发生了就会造成极大的损失，但通常不会发生。因此，将其处理为0-1变量，即只关注其发生与不发生的情况。同理可得：（j）=18.3，=27.1取显著性水平α=0.05，则（1）=3.84。因此，这2个指标也具有马尔科夫性。

选取2012年8月23日这一样本作为输入值，预测2012年8月26日的风险发生概率分布，并将预测结果处理后与实际值比较，见表2。

表2　马尔科夫链预测结果与实际值的比较Table 2 Comparison between the prediction by Markov chain and the actual value

表2的实验结果表明，马尔科夫链的预测效果较好，吻合程度较高，符合率约为82%。

3.2贝叶斯网络预测

Prediction by Bayesian network

若仅使用贝叶斯网络进行预测，其结果如表3所示。

表3　贝叶斯网络预测结果与实际值的比较Table 3 Comparison between the prediction by Bayesian network and the actual value

表3的结果表明贝叶斯网络的预测结果显然与实际值相差很大，符合率约为46%。

3.3新方法预测

Prediction by the new method

将表2中的马尔科夫链的预测结果作为证据输入到贝叶斯网络中，预测2012年8月26日上层指标的风险。图 1的预测结果显示：以用马尔科夫链预测的2012年8月23日底层指标分布为证据输入贝叶斯网络计算得到8月26日各上层指标的概率分布如表4所示，预测值与实际值100 % 吻合。

表4　指标风险发生的概率分布Table 4 Probability distribution of risk indices

图1　贝叶斯网络模型Fig. 1 Bayesian network model

4　结论

Conclusions

（1）在分别研究了马尔科夫链和贝叶斯网络2种预测方法的基础上，创新地将其融合形成了一种纵横预测的新方法。

（2）该方法继承了马尔科夫链纵向预测底层指标的准确性和贝叶斯网络横向准确预测对应上层指标状态的优点，顺利解决了钻井指标体系中因上层指标数据缺乏而不能预测的问题。

（3）应用现场实地采集的数据，对新方法进行了检验，结果显示新方法的预测结果符合实际。

References:

［1］ KHAKZAD N， KHAN F， AMYOTTE P. Quantitativerisk analysis of offshore drilling operations: a bayesian approach［J］. Safety Science， 2013， 57（8）: 108-117.

［2］ ZHAO Q， ZHANG H， FAN J. Human factor risk quantification for oil and gas drilling operation［J］. Procedia Engineering， 2011， 40（18）: 312-317.

［3］ ABIMBOLA M， KHAN F， KHAKZAD N. Dynamic safety risk analysis of offshore drilling［J］. Journal of Loss Revention in the Process Industries， 2014， 30（3）: 74-85.

［4］ GIERCZAK M. The qualitative risk assessment of mini，midi and maxi horizontal directional drilling projects ［J］. Tunnelling and Underground Space Technology， 2014， 44 （5）: 148-156.

［5］ 李玮，赵菁菁，高磊，孙维国，刘景宇.基于Android 的钻井风险实时诊断与评估系统［J］.石油钻采工艺，2015，37（4）：5-8. LI Wei， ZHAO Jingjing， GAO Lei， SUN Weiguo， LIU Jingyu. Realtime diagnosis and evaluation system for drilling risk based on Android［J］. Oil Drilling & Production Technology， 2015， 37（4）: 5-8.

［6］ 管志川，赵廷峰，胜亚楠，魏凯.复杂地层钻井风险程度判别方法研究［J］.石油钻采工艺，2015，37（3）：11-14. GUAN Zhichuan， ZHAO Tingfeng， SHENG Ya’nan，WEI Kai. Research on method of discriminating drilling risk degree in complex formations［J］. Oil Drilling & Production Technology， 2015， 37（3）: 11-14.

［7］ LAVASANI S M. Fuzzy risk assessment of oil and gas offshore wells［J］. Process Safety and Environmental Protection， 2011， 89（5）: 277-294.

［8］ SWEENEY M L， PARKER A， HABER T L K. Application of markov chain monte carlo analysis to biomathematical modeling of respirable dust in us and uk coal miners［J］. Regulatory Toxicology and Pharmacology， 2013， 66（1）: 47-58.

［9］ JAVAN T D ， BAO J ， HUDON N， YANG R. Collective dynamics modeling of poly disperse particulate systems via markov chains ［J］. Chemical Engineering Research and Design， 2013， 91（9）: 1646-1659.

［10］ ELEGBEDE C F， PAPADOPOULOS Alexandra，GAUVREAU Julie， CREPET Amélie. A bayesian network to optimise sample size for food allergen monitoring［J］. Food Control， 2015， 47（1）: 212-220.

［11］ WEE Y Y， CHEAH W P， TAN S C， WEE K. A method for root cause analysis with a bayesian belief network and fuzzy cognitive map［J］. Expert Systems with Applications， 2015， 42（1）: 468-487.

［12］ LI Zhongxing ， ZHU Jingjing， SHEN Xufeng，ZHANG Cong， GUO Jiwei. Fault diagnosis of motor bearing based on the bayesian network［J］. Procedia Engineering， 2011， 40（16）: 18-26.

［13］ 王瑞勤.风险分析——钻井作业实施HSE管理的核心［J］.安全、健康和环境，2003，3（6）：32-33. WANG Ruiqin. Risk analysis—— the core of the implementation of hse management in drilling operations ［J］. Safety， Health & Environment， 2003， 3（6）: 32-33.

［14］ 李琪，王涛，王再兴，张成秀，张立君. 一种新的钻井井身质量评价方法［J］. 石油钻采工艺，2015，37（2）：1-4. LI Qi， WANG Tao， WANG Zaixing， ZHANG Chengxiu，ZHANG Lijun. A new evaluation method for wellbore quality［J］. Oil Drilling & Production Technology，2015， 37（2）: 1-4.

［15］ 刘正礼，胡伟杰. 南海深水钻完井技术挑战及对策［J］.石油钻采工艺，2015，37（1）：8-12. LIU Zhengli， HU Weijie. Countermeasures and challenges of deepwater drilling and completion technology in South China Sea［J］. Oil Drilling & Production Technology， 2015， 37（1）: 8-12.

［16］ 何玉发，周建良，蒋世全，杨秀夫，金颢. 深水井测试安全控制技术［J］. 石油钻采工艺，2015，37（1）：163-165. HE Yufa， ZHOU Jianliang， JIANG Shiquan， YANG Xiufu， JIN Hao. Safety control technology of deepwater oil and gas well testing［J］. Oil Drilling & Production Technology， 2015， 37（1）: 163-165.

［17］ 廖普明. 基于马尔科夫链状态转移概率矩阵的商品市场状态预测［J］. 统计与决策，2015，26（2）：97-99. LIAO Puming. Prediction of markov chain state transtion-probablity matrix based on commodity market ［J］. Statistics and Decision， 2015， 26（2）: 97-99.

［18］ 方卫东，怀博. 沪深300指数马氏性检验及预测［J］.科学技术与工程，2011，11（20）：4833-4835. FANG Weidong ， HUAI Bo. Prediction and analysis of shanghai and shenzhen 300 index based on weighted markov chain［J］. Science Technology and Engineering， 2011， 11（20）: 4833-4835.

［19］ 张松. 基于马尔科夫链的ZigBee信道选择算法的研究［D］.上海：上海海洋大学，2014. ZHANG Song. Zig Bee channel selection algorithm research based on Markov Chain［D］. Shanghai: Shanghai Ocean University， 2014.

［20］ 高波，王连亮，罗懋康. 基于软证据的贝叶斯网络推理［J］. 统计与决策，2014，14（21）：32-35. GAO Bo， WANG Lianliang， LUO Maokang. Bayesian network inference based on soft evidence［J］. Statistics and Decision， 2014， 14（21）: 32-35.

（修改稿收到日期 2016-03-21）

〔编辑 薛改珍〕

Drilling risk prediction based on Markov chain and Bayesian network

ZHONG Yihua， LIU Yuxin， LIN Xuxu
School of Science， Southwest Petroleum Uniνersity， Chengdu， Sichuan 610500， China

Drilling operation is a risky and costly process， during which many uncertainties may cause a serious accident. In order to prevent or mitigate the risks and thereby avoid economic loss， it is necessary to predict these uncertainties. In this paper， the existing drilling risk prediction methods （e.g. Markova chain and Bayesian network） were reviewed， and then a new drilling risk prediction method was proposed by integrating the Markova chain and Bayesian network based on the index system adopted on site. This new method can be used predict the risk of drilling accident vertically and horizontally， and also overcome the shortage which occurs when the upper indices are processed only by using Markova chain. Moreover， it provides the theoretical basis for the risk diagnosing， monitoring and controlling. The case study shows that this new method is correct and feasible. The goodness of fit between the vertical prediction and the actual data of the integrated method is higher than that of Markova chain （82%） and Bayesian network （46%）.

drilling risk； risk prediction； Markov chain； Bayesian network

刘雨鑫（1992-），2014年毕业于西南石油大学数学与应用数学专业，现从事数据挖掘及应用统计研究。通讯地址：（610500）四川省成都市新都区新都大道8号西南石油大学明理楼A522室。 E-mail：18782026781@163.com述分析及评估方面［1-6］；但在风险估计和预测方面的研究不多，S. M. Lavasani等少数学者利用层次分析和证据推理方法评估了海上石油钻井风险［7］。马尔科夫链是进行随机事件风险预测的有力工具［8-9］，具有较高的预测精度，但不能诊断风险发生的原因；贝叶斯网络是一种将概率知识和图论相结合，表示事件之间的不确定性影响的网络结构，广泛用于风险的原因分析和预测［10-12］，但其预测能力较差。笔者将马尔科夫链和贝叶斯网络方法融合，提出了从纵、横两方面进行钻井风险预测的新方法。利用该方法，不仅可预测钻井风险，而且还给出了诊断、监测和控制引起风险的主要原因。

TE28

A

1000 - 7393（ 2016 ） 03 - 0291- 05

10.13639/j.odpt.2016.03.003

ZHONG Yihua， LIU Yuxin， LIN Xuxu. Drilling risk prediction based on Markov chain and Bayesian network ［J］. Oil Drilling & Production Technology， 2016， 38（3）: 291-295.

西南石油大学创新团队基金项目：“最优化理论与控制”（编号：2013XJZT004）。

钟仪华（1965-），2011毕业于西南石油大学石油工程计算技术专业，现从事石油工程计算技术和数据挖掘的研究及教学工作，教授，硕士生导师。通讯地址：（610500）四川省成都市新都区新都大道8号西南石油大学理学院。E-mail：zhongyh_65@126. com

引用格式：钟仪华，刘雨鑫，林旭旭.基于马尔科夫链和贝叶斯网络的钻井风险预测［J］.石油钻采工艺，2016，38（3）：291-295.