混合遗传算法在弹箭气动参数优化的应用

刘霖赵学良靳克马庆坤闫志强

混合遗传算法在弹箭气动参数优化的应用

刘霖1赵学良2靳克2马庆坤2闫志强2

1、山西中北大学机电工程学院2、河南豫西工业集团

弹箭气动参数是影响弹箭飞行运动的重要因素，因此获取准确的弹箭气动参数对弹箭的研制极为重要。在射击实验之后，弹箭参数的辨识实际上就是一个参数优化的过程，但是传统的优化方法在弹箭气动参数优化过程中，很容易陷入局部最优解，而无法准确得出参数，同时遗传算法具有很好的全局优化能力，但是在局部寻优上很慢，因此将二者相结合形成的混合遗传算法来进行弹箭参数优化，效果比单一算法好。

气动参数；优化；混合遗传算法

引言

弹箭在空气中运动时，所受到的空气动力是影响其运动轨迹、速度等的主要因素之一。要想研究弹箭在空气中的运动规律，首先要得到弹箭的气动力特性。获取弹箭气动力参数的常用方法有三种：理论计算法、风洞吹风试验法和射击试验法。其中理论计算法和风洞实验法因为其本身的局限性，需要有很多假设条件，造成误差较大。

射击实验法，通常是通过各种仪器测量到一系列的数据，这些数据包含弹丸飞行过程中的坐标、速度和转速。再通过弹丸状态方程，解算弹箭气动力参数。但其实现比较繁琐，在测试仪器和设备方面要求较高。同时试验原理和数据采集的准确性对求取的精度影响较大，得到的参数不能直接用于工程应用。

本文基于最优化理论，同时结合最小二乘法拟合的思想，以射击实验法得到的气动力参数作为设计变量，以计算弹道与实测的弹道模型之间的残差平方和作为优化模型的目标函数，只要使得目标函数极小，就能找到一组最能反映实际弹道模型的气动力参数。

1优化流程

本文优化的设计变量是射击实验法得到的气动力参数，在优化求解中，由优化算法控制不断改变其数值大小及数值变化趋势，从而获得最优的目标函数。在气动力参数中，阻力系数Cx对弹道模型的影响最大，这里选用它作为本次仿真的设计变量。

目标函数是评价优化问题好坏的准则，最优化问题的本质就是寻找到一组设计变量，使对应的目标函数值极大或者极小。在靶场射击试验中获得的火箭弹的飞行数据测量值（ti，xci，yci，zci），通过优化算法得到一组设计变量，代入四自由度弹道方程计算，也会获得一组弹道数据（ti，xi，yi，zi）。根据最小二乘法理论，得残差和

以此作为目标函数，只要使得ε的值极小，此时通过弹道方程解算出来的弹道，与实测弹道重合度最好，可以认为这组气动力参数就是该弹从实测数据中提取出（

）来的真实气动力参数。具体优化过程如图1。

图1　优化流程

2优化算法

优化设计方法有很多，但是它们有各自的特点局限性。传统的优化算法，计算效率比较高，但对问题的数学模型有很大依赖性，优化过程的收敛对初始设计点的选择有很大关系，很容易陷入局部最优解。对于像弹箭总体参数优化这种复杂工程系统，模型相对比较复杂，对优化算法的选择要求十分苛刻，使用传统优化算法得到的最终优化解很可能是局部最优的，很难达到全局最优解。

遗传算法主要思想是借助于生物进化过程中“适者生存”的原则，模仿生物进化的遗传繁殖机制进行寻优，具有很好的全局搜索能力，可以快速地将空间中的全体解搜索出，能较大程度地避免陷入局部最优解，并且利用它的内在并行性，可以方便地进行分布式计算，加快求解速度。但在局部寻优上，因为依靠算子交叉和算子变异，所以效率很低，在实际应用中，容易产生早熟收敛的问题。

霍克-吉维斯法（hooke-jeeves）属于直接搜索法，在设计点周围的搜索效率很高；由于在探索阶段使用的寻优步长很大，在搜索初期可以搜索到的设计变量取值空间比使用梯度优化算法时的更大；对于中等规模设计变量和中等非线性优化问题，hooke-jeeves方法特别适用。但是其对初始设计点要求较高，不合适的初始设计点有可能使寻优落入局部最小解；同时对于仿真计算耗时比较长的参数优化问题，hooke-jeeves方法并不适用。

因此，采用霍克-吉维斯法与遗传算法相结合的方法，可以同时发挥到两种算法的优点，对弹道参数进行优化，可以快速有效得到其最优解。

Isight软件算法库中集合了多种优化算法，具有可移植性、应用过程中灵活度高、人工建模工作量小、辨识结果误差较小等优点，这里我们利用了isight软件与弹道程序相结合组成，设计变量（即阻力系数Cx）算法流程如图2。

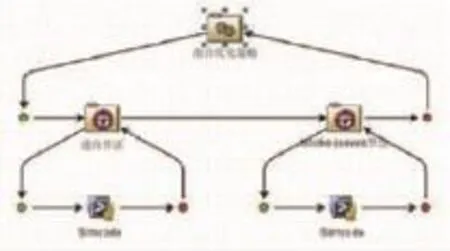
图2　组合优化算法流程图

3仿真计算结果

本仿真使用四自由度弹道方程组，即修正质点弹道方程。根据修正质点弹道方程，计算出弹箭飞行时的质心速度、质心位置坐标的理想弹道，作为本次仿真样本数据。采用弹丸设计理论阻力系数经验值作为初值，根据上述优化算法流程，分别使用hooke-jeeves算法、遗传算法和混合遗传算法三种不同的算法对阻力系数进行优化计算，对比结果如表1所示。

表1　三种算法对比结果

图3～图5是三种不同算法下，计算出的阻力系数Cx随马赫数Ma的变化规律与真值（即理想弹道的Cx变化值）的对比图。

图3　hooke-jeeves算法优化结果

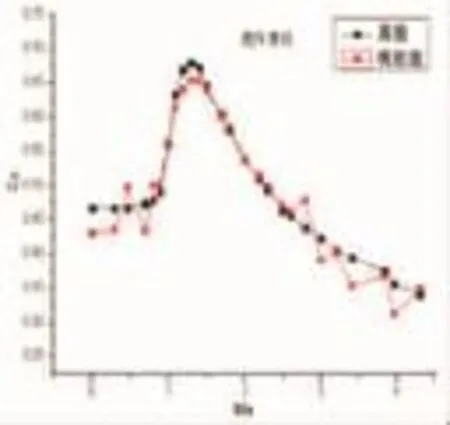
图4　遗传算法优化结果

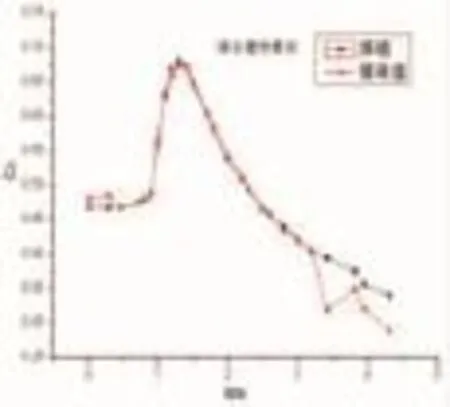
图5　混合遗传算法优化结果

通过上述计算结果，对比三种算法可以发现，混合遗传算法优化所得到的阻力系数Cx更接近于真值。通过表1对比，遗传算法所用时间最长，且陷于局部最优解。hooke-jeeves算法稍好，但与混合遗传算法的结果相比，其精度不高。混合遗传算法在寻优速度上，与hooke-jeeves算法相当，但计算精度要强于遗传算法和hooke-jeeves算法，证明混合遗传算法可用于弹箭气动参数优化。

［1］王晓鹏，万敏.一种基于遗传算法的动力学系统辨识方法［J］.飞行力学，2003.

［2］王小平，李续武.遗传算法—理论、应用与软件实现［M］.西安：西安交通大学出版社，2002.

［3］蔡金狮.飞行器系统辨识［M］.北京：宇航出版社，1995.

［4］韩子鹏等.弹箭外弹道学［M］.北京：北京理工大学出版社，2008.

［5］周明，孙树栋.遗传算法原理及应用［M］.北京：国防工业大学出版社.

3结果分析

72%烯酰·锰锌可湿性粉剂1211、1299、1387g/hm2处理对黄瓜霜霉病的防效分别为66.78%、75.76%、72.58%，方差分析结果表明，试验药剂72%烯酰·锰锌可湿性粉剂1299 g/hm2处理防效、1387 g/hm2和80%烯酰吗啉水分散粒剂264 g/hm2处理防效差异显著，与80%代森锰锌是可湿性粉剂2520 g/hm2处理差异不显著；72%烯酰·锰锌可湿性粉剂1387 g/hm2处理、两单剂对照处理间差异不显著，72%烯酰·锰锌可湿性粉剂1211 g/hm2与其他各处理间差异极显著。

药剂评价：试验结果表明，72%烯酰·锰锌可湿性粉剂可有效防治黄瓜霜霉病，其防效优于两单剂对照，试验范围内对黄瓜安全，未见不良影响，可以推广应用。

技术要点：在黄瓜霜霉病发病初期喷雾防治，间隔7～10d左右，连用2～3次。推荐用量为有效成分1299～1387 g/hm2。

刘霖，1984年5月出生，湖北利川人，硕士，研究方向：兵器工程。