履带车辆悬挂系统稳定性分析

许　奎，王鑫磊

(1. 中国北方车辆研究所，北京100072； 2. 中国北方工业公司，北京100053)



履带车辆悬挂系统稳定性分析

许奎1，王鑫磊2

(1. 中国北方车辆研究所，北京100072； 2. 中国北方工业公司，北京100053)

履带车辆悬挂系统不仅直接影响到车辆的平顺性和舒适性，而且对履带车辆的稳定性能和行进间射击精度有着重要的影响。基于履带车辆建立了路面模型和车辆悬挂系统的二自由度动力学模型，采用Simulink对悬挂系统动力学模型进行仿真计算，并通过改变悬挂的阻尼刚度和弹簧刚度来分析其对车辆稳定性和车辆射击精度的影响，为悬挂系统的设计提供基础。

悬挂系统Simulink仿真稳定性射击精度

履带车辆的悬挂系统不仅将车体和负重轮弹性地连接起来， 而且传递了作用在负重轮和车体间的一切力和力矩，并缓和了车辆行驶时经过负重轮传递到车体上的冲击力，从而减少了车体的振动，提高了车辆的行驶稳定性和车辆行进间的射击精度[1]。因此，履带车辆的悬挂系统不仅对车辆的舒适性和平稳性有着重要的作用，而且对车辆的操作稳定性和行进间射击精度有直接的影响。

1　路面模型的建立

国内外的许多测量分析表明，为了描述车辆振动输入的路面不平度，国际标准协会在《路面不平度表示方法草案》标准中, 建议采用路面功率谱密度来描述其统计特性，并用下式作为拟合功率谱密度的表达式[2]：

Gq(n)=Gq(n0)(n/n0)-w

(1)

式中：n—空间频率,表示每1m长度中包含n个波长；n0—参考空间频率，n0=0.1m-1；w—频率指数，通常取w=2；Gq(n0)—路面不平度系数(即参考空间频率n0下的路面功率谱密度值)，m3。

本文使用白噪声模拟激励，路面随机激励的时域模型使用一阶滤波，其位移表达式[3]：

(2)

式中，xr为路面不平度位移，m；f0为下截止频率，Hz； u为车辆速度，m/s；w(t)为随机白噪声。

选择在D级路面上进行随机路面仿真，则Gq(n0)=1 024×10-6m3,下截止频率f0取为0.062 8Hz，车速u取10m/s。路面激励模型如图1所示。

图1　路面激励模型

则得到D级随机路面时域结果如图2所示。

图2　10 m/s时D级随机路面位移时域变化

2　悬挂系统模型建立

以车辆静止平衡时悬挂的质心为坐标原点建立车体平面坐标系。设车辆水平行驶方向为X轴(正向为车辆行驶方向)，与地面垂直的方向为Z轴(正向垂直地面向上)，而与X、Z所在平面垂直的方向为Y轴，且X，Y，Z轴的正向符合右手法则。由于履带车辆通常越野行驶在一个复杂的环境中，承受着随机的振动响应，因此需要将其进行合理的简化。一般从三个方面来描述车辆的振动情况：车身的垂直振动情况、车身绕Y轴的俯仰振动情况和车身绕X轴的侧倾振动。然而，在车辆的行驶过程中，对履带车辆行驶影响较大的是车身的垂直振动和车身绕Y轴的俯仰振动，特别是对行进间射击精度影响较大。因此在建立悬挂模型时主要考虑这两个方向的振动对车辆稳定性和车辆行进间射击精度的影响[4-5]。

2.1悬挂模型建立的基本假设

由于履带车辆在越野行驶时要承受复杂多变的振动响应和随机激励，在这种情况下，想要快速地分析其随机振动过程对履带车辆稳定性和行进间射击精度的影响，并建立准确的数学模型，就要对振动做出如下假设[6]：

1)不考虑车辆在行驶过程中自身的变形，且路面为刚体；

2)不考虑车身绕X轴的侧倾振动，并假设车体部分关于经过质心的纵轴线对称；

3)不考虑履带对车体振动的影响；

4)各轮悬挂的减振器的阻尼系数相同，均为C；各悬挂的弹簧刚度相同，均为K。

图3　履带车辆悬挂系统2自由度模型

2.2履带车辆悬挂系统动力学方程

式中：M—车体的质量；Iy—车体绕Y轴的转动惯量；Z—车体垂直方向的位移；φ—车体的纵向俯仰运动的角位移；C—悬挂的阻尼刚度；K—弹簧的刚度；L1、L2—对应负重轮重心至车体重心的距离；xr—路面不平度位移。

其中：

3　仿真分析

根据悬挂系统的动力学方程和状态方程，采用Matlab/Simulink建立如图4仿真模型进行仿真计算。

图4　悬挂系统仿真模型

当车辆以10 m/s的速度行驶在E级路面时得到的仿真结果如图5-图10。

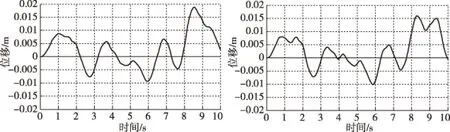
图5　车身位移响应　　　　　图6　车身位移响应曲线(K)　　　　　　　　　　曲线(2K)

图7　车身位移响应　　　　　图8　车身角位移响曲线(10K)　　　　　　　　　应曲线(K)

图9　车身角位移响　　　　图10　车身角位移响应应曲线(2K)　　　　　　　　曲线(10K)

图中给出了履带车辆悬挂系统在K改变时，车身垂直位移和俯仰角位移的变化，从图中可以看出，随着K的增大，车身的垂直位移有所减小，但幅度不大，而俯仰角位移却增大较多，而且弹簧刚度较大时，车身垂直位移和车身俯仰角位移的振动频率明显增大，不利于车辆的稳定性和车辆行进间的射击精度。图11-图14给出了履带车辆悬挂系统在C改变时，车身的垂直位移和俯仰角位移的变化，从图中可以得出，当悬挂阻尼刚度增加时，车身的垂直位移有所减小，但车身的俯仰角位移却有所增加，而且位移和角位移的振动频率都明显增加，同样不利于车辆的稳定性和车辆行进间射击精度。总之，履带车辆悬挂系统的弹簧刚度和阻尼刚度都会对车身垂直位移和车身俯仰角位移产生影响，进而影响到火炮的稳定精度和车辆行进间射击精度。

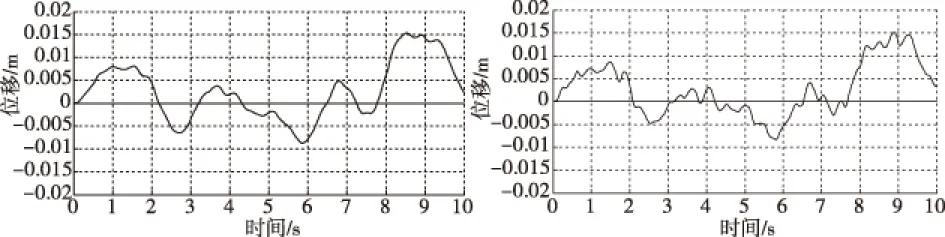
图11　车身位移响应　　　图12　车身位移响应曲线(2C)　　　　　　　　曲线(10C)

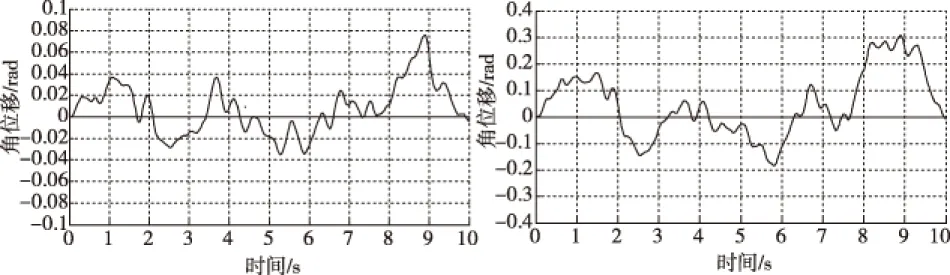
图13　车身角位移响应　　　图14　车身角位移响曲线(2C)　　　　　　　　　应曲线(10C)

4　火炮的稳定精度

火炮的稳定精度定义是：坦克在中等起伏路面上以中等速度行驶时，火炮摆动振幅的算术平均值。由于火炮都有一定的射击精度，坦克在行进间射击时，火炮的摆动就会对射击精度产生影响。而火炮存在的稳定精度问题主要是由两个方面造成：1)系统的干扰误差。即车辆在行进时，炮塔和火炮会在摩擦力矩的作用下，不断偏离原来稳定的位置，而稳定装置又会产生稳定力矩不断令其返回到原来的位置，从而使火炮出现了微微摆动的现象，进而产生系统误差。2)陀螺仪信号误差。由于在稳定状态下，火炮在上下摆动时，陀螺仪底座和外环间会产生相对运动，而且外环轴承也存在一定的摩擦力矩，从而促使内环在火炮上下摆动产生相应的摆动，从而产生误差信号[8]。如图15为火炮稳定装置的工作过程。

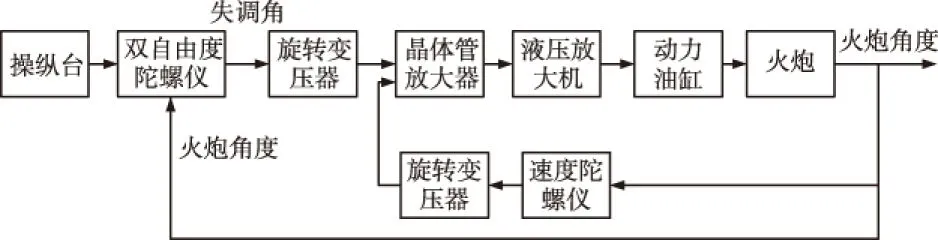
图15　火炮稳定装置工作过程

从火炮的稳定装置工作过程可以看到，当火炮的偏离角度越大，变化频率越高，火炮稳定时所需稳定力矩越大，而且火炮的振动频率越高，不利于火炮的稳定，使火炮的稳定精度减小，从而降低了车辆行进间射击精度。

5　结论

悬挂系统的弹簧刚度和阻尼刚度对车身稳定性有着决定性的影响，并最终影响到车辆的舒适性和行进间射击精度，如何匹配一个合适的弹簧刚度和阻尼刚度对悬挂系统十分重要。由于车体的振动，会使车辆的稳定性能变差，同时会产生系统干扰误差和陀螺仪误差信号，且车体的振动越大，产生的误

差信号也越大，火炮的稳定精度越低，从而使车辆行进间射击精度减小。经过仿真分析可知，当该履带车辆悬挂系统的弹簧刚度为K，减振器的阻尼刚度为2C时，车辆的稳定性是最好的，从而使得车辆行进间射击精度也最高。

[1]闫清东，张连第，赵毓芹,等.坦克构造与设计[M].北京：北京理工大学出版社，2007.

[2]余志生.汽车理论[M].北京:机械工业出版社,2006.

[3]徐龙辉.履带式自行火炮行进间振动特性及控制研究[D].南京理工大学，2013.

[4]明鑫.履带式车辆主动悬架研究[D].长春：长春吉林大学，2011.

[6]熊超，郑坚，张进秋,等. 履带车辆半主动悬挂系统建模与仿真[J].兵工自动化，2005,24(1):9-11.

[7]杨杭旭.车辆悬挂系统的状态反馈控制稳定性分析[J].林业机械与土木设备，2014(5)：43-44.

[8]朱竞夫，赵璧君，王钦钊.现代坦克火控系统[M].北京：国防工业出版社，2003.

Stability analysis of tracked vehicle suspension system

XU Kui, WANG Xinlei

Tracked vehicle suspension system not only directly affects the comfort index of the vehicle, but also affects its stability and firing accuracy in moving. We established a model of the road surface and a two-degree-of-freedom dynamic model of the tracked vehicle suspension system, and carried out simulated calculation of the models by Simulink. By analyzing the effects of damper stiffness and spring stiffness on the stability and the firing accuracy of the vehicle, we provided reference for the design of vehicle suspension systems.

suspension system，Simulink simulation，stability，firing accuracy

TJ811

A

1002-6886(2016)04-0028-04

许奎(1989-)，男，在读硕士研究生，研究方向：混合动力推进总体技术。

2016-01-15