旋转导向钻井稳定平台的RBF网络滑模变结构控制

霍爱清，邱 龙，2，汪跃龙

(1.西安石油大学 电子工程学院，陕西 西安 710065； 2.陕西烽火实业有限公司，陕西 西安 710075)



旋转导向钻井稳定平台的RBF网络滑模变结构控制

霍爱清1，邱 龙1，2，汪跃龙1

(1.西安石油大学 电子工程学院，陕西 西安 710065； 2.陕西烽火实业有限公司，陕西 西安 710075)

针对旋转导向钻井稳定平台存在的摩擦问题带来的不确定性,提出一种基于RBF神经网络的自适应滑模变结构控制方法,以提高稳定平台控制的精确性和抗干扰能力。使用RBF神经网络对稳定平台模型中的不确定性进行逼近，通过设计RBF网络节点的唤醒与激活阈值来减少网络规模，同时设计权值调整的自适应律，并结合滑模控制增强系统的鲁棒性。分别采用一般滑模变结构控制方法和RBF神经网络滑模变结构控制方法进行仿真实验，结果表明，RBF神经网络滑模变结构控制方法能够有效地逼近控制对象模型，有较强的鲁棒性。

旋转导向钻井稳定平台控制；RBF神经网络；滑模变结构；节点激活

霍爱清，邱龙，汪跃龙.旋转导向钻井稳定平台的RBF网络滑模变结构控制[J].西安石油大学学报(自然科学版)，2016，31(4):103-108.

HUO Aiqing,QIU Long,WANG Yuelong.Sliding mode variable structure control of stabilized platform in rotary steerable drilling system based on RBF neural network [J].Journal of Xi'an Shiyou University (Natural Science Edition),2016,31(4):103-108.

引　言

稳定平台控制是旋转导向钻井系统的关键环节。在钻井过程中,受井下复杂多变的工作环境影响，干扰稳定平台系统控制精度的参量较多，同时稳定平台跟随钻柱一直处于旋转状态，具有旋转摩擦的非常规运动特性，因此稳定平台受摩擦扭矩变化的影响较大。为了使稳定平台具有稳定和快速调整钻井工具的工具面角的能力，研究可靠的控制策略是十分必要和关键的。

汪跃龙[1]研究了旋转导向钻井结构中偏心力矩对系统的作用，并在PID控制中增加了反馈线性化环节，使非线性的偏心力矩转换成线性的，从而优化了对稳定平台的控制。然而传统的PID控制对确定性系统模型可以达到较好的控制效果，但是在钻井过程中钻井液脉冲压力不可能保持固定值，稳定平台控制系统的结构产生多种摩擦，这些因素会带来过程对象模型的某些不确定性，进而会影响对系统的精确控制。而单纯使用滑模变结构控制虽然能够避免未知扰动带来的不确定性，但是需要寻求消除抖振的有效方法。Yong Feng[2]研究了Terminal滑模控制消除抖振，通过设计一种动态非线性滑模面方程实现，但该方法中非线性函数的引入使得控制器在实际工程中实现困难，而且如果参数选取不当，会出现奇异问题。霍爱清[3]将模糊控制和滑模变结构控制相结合，采用自适应模糊控制器来逼近等效控制器对导向钻井稳定平台进行控制，并利用模糊控制来消除滑模控制器在切换面产生的抖振。但是该方法只是对控制器进行了等效逼近设计，并没有对稳定平台系统模型进行逼近。

本文提出滑模变结构控制器与RBF神经网络自适应控制相结合对旋转导向钻井稳定平台进行控制[4-7]。主要是利用RBF神经网络具有高度非线性的连续时间动力系统这一特点[8]，以及具有很强的自学习功能和对非线性系统的强大映射能力，对稳定平台数学模型进行逼近。设计了自适应律对神经网络的权值进行学习，同时使用节点激活与催眠作用以减少网络结构，提高网络运算速度。最后结合滑模控制提高系统鲁棒性和抗干扰能力。

1　稳定平台模型

1.1稳定平台被控对象模型

根据稳定平台在井下的工作方式，稳定平台可以被看作发电机式的单轴惯性稳定平台系统[9-11]。稳定平台广义被控对象框图如图1所示。

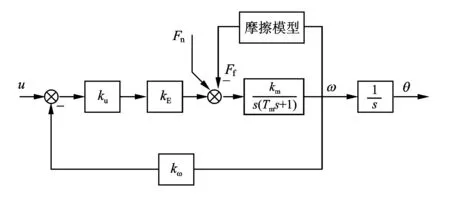
图1　稳定平台广义被控对象模型Fig.1　Generalized controlled object model of stabilized platform

图1中，ku为PWM脉宽调制系数，kE为电枢电流与电磁力矩之间的比例常数，kω为陀螺传感器转换系数，Ff为摩擦力矩，Fn为其他干扰力矩，km为电机传动系数，Tm为电机机电常数。

其中，J为转动惯量，Ce为反电动势系数，Cm为电机转矩系数，R为电枢电阻，f为黏性摩擦系数。

则稳定平台广义被控对象数学模型可写为

(1)

1.2上下盘阀摩擦力矩

根据稳定平台的结构及在井下工作状态,上下盘阀相对旋转一周时,导流孔依次切出、切入，使得上下盘阀贴合面积发生变化，产生摩擦力矩M。

设装配完成后弹簧的压紧作用力F恒定，记在1个孔导通时的上下盘阀摩擦接触面积为A0，摩擦力矩为M，上下盘阀间的摩擦因数为η，则上下盘阀交变摩擦力矩[11]

(2)

式中，r为导流孔半径,ΔS为上下盘阀贴合面积，随转速变化关系为：

(0<ωt<π/6)。

(3)

式中，β为切出角,由三角函数关系得

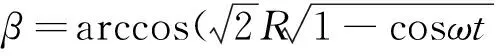
其中R为导流孔圆心运动半径。

在转速为30r/min时，上下盘阀相对旋转一周时的摩擦副动态阻力矩变化如图2所示。

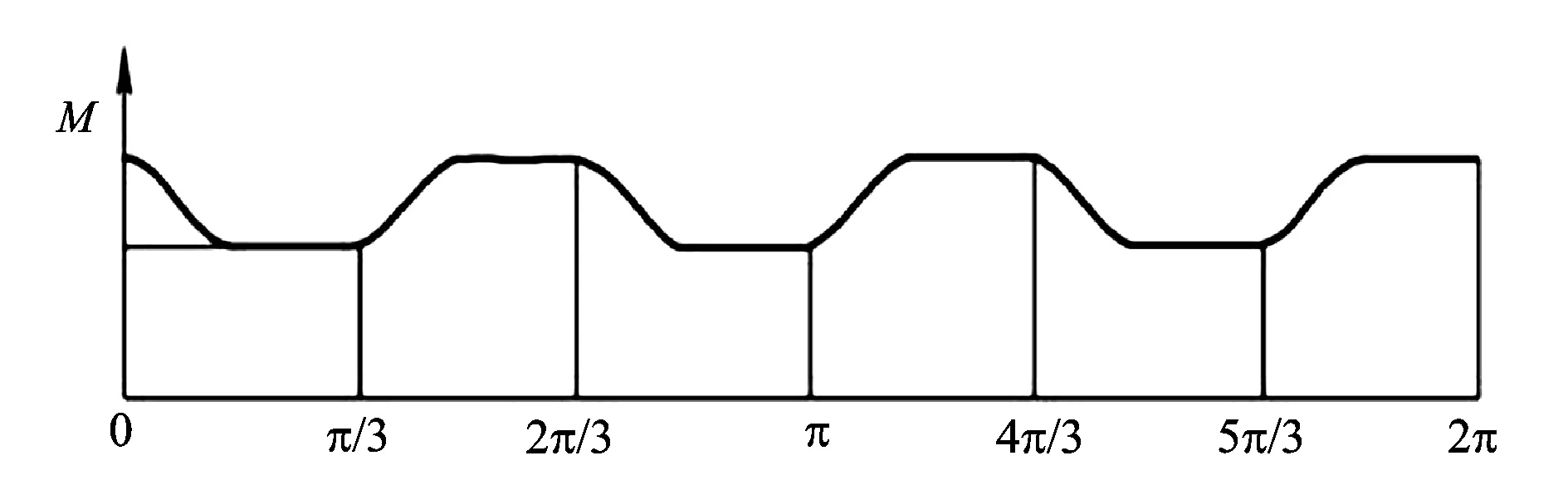
图2　相对旋转一周时上下盘阀交变摩擦力矩Fig.2　Alternating friction torque between the upper valve and lower valve when relatively rotating a cycle

2　控制器设计

2.1控制器总体设计框图

RBF自适应滑模变结构控制器的设计思路是利用自适应律来调节RBF网络的权值来逼近系统的未知结构，并与滑模变结构控制策略相结合，来消除滑模控制产生的抖振，增强系统的鲁棒性。设计框图如图3所示。

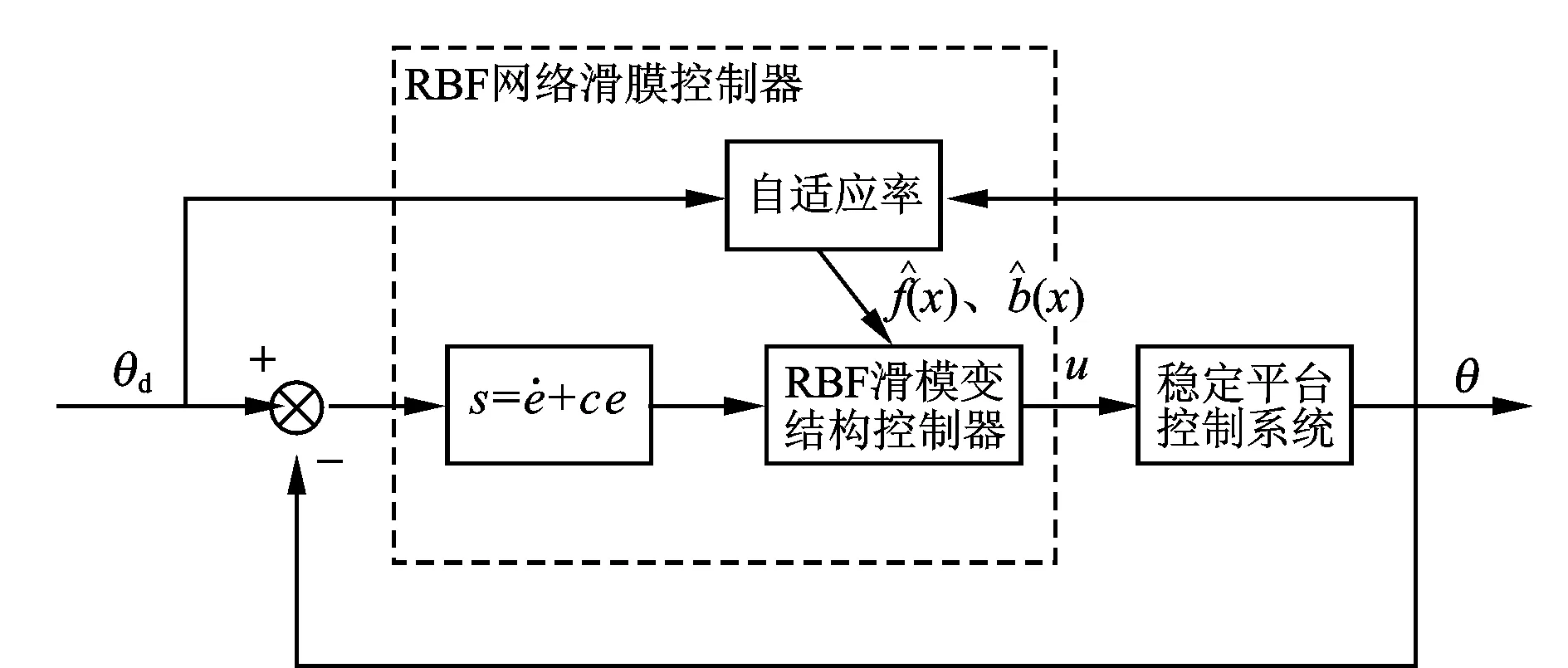
图3　RBF神经网络滑模变结构自适应控制器框图Fig.3　Block diagram for adaptive sliding mode variable structure controller based on RBF neural network

2.2变结构控制器设计

二阶不确定非线性系统

(4)

设x1=θ,理想工具面角为θd,则误差为

e=θd-θ 。

(5)

取滑模函数为

(6)

对滑模函数s求导，得

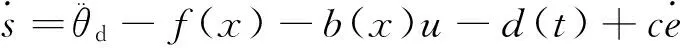
设计理想的滑模控制为

u=ueq+un，

(7)

其中ueq为等效控制项，un为切换控制项。

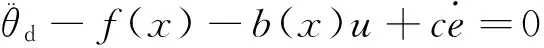
则有

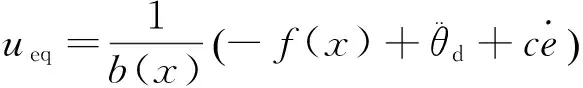
(8)

设计切换控制器为

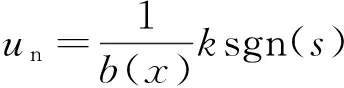
(9)

其中，k为增益项，k >0。

总的控制器设计为

u=ueq+un，

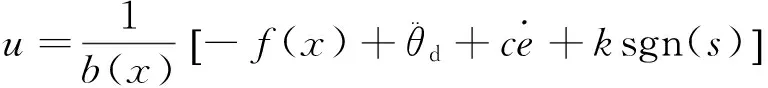
(10)

2.3RBF神经网络自适应滑模控制器设计

RBF神经网络是一种具有单隐层的高效的三层前馈式神经网络，具有最佳逼近性能和全局最优特性，且网络结构简单，训练速度快。

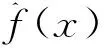
则有

(11)

(12)

其中，hi(x)为RBF网络输出，

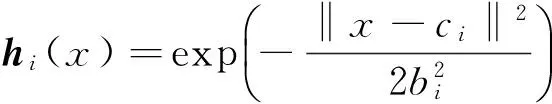
其中，x为RBF网络输入，ci表示RBF网络第i个神经元的中心位置，bi为第i个神经元的宽度，wfT和wbT为RBF网络权值。

将式(11)和式(12)代入式(10)，得

(13)

由式(5)、(6)、(11)、(12)、(13)，得

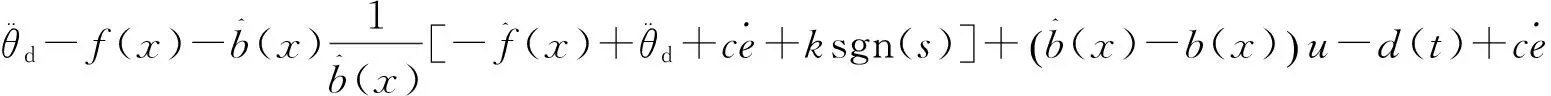
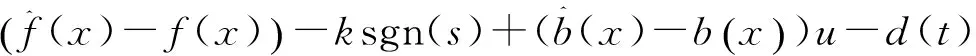
(14)

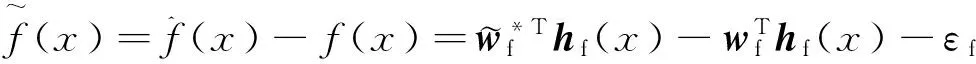
(15)

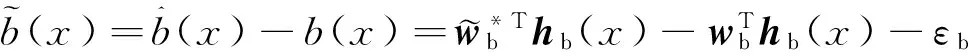
(16)

令

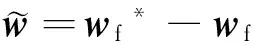
(17)

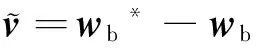
(18)

将式(15)、(16)、(17)、(18)，代入式(14)，得

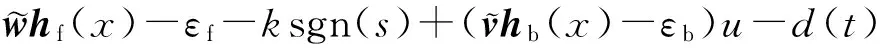
(19)

2.4自适应律设计

定义Lyapunov函数为

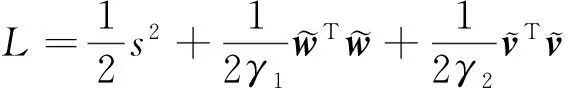
(20)

其中γ1>0,γ2>0。

对Lyapunov函数求时间导数，并代入式(14)，得

(21)

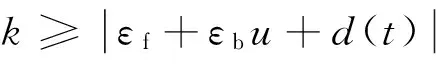
此时由式(21)取自适应率为

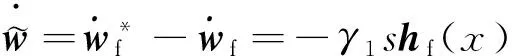
(22)

(23)

2.5节点激活与催眠技术

RBF网络设计的核心是选择合适的隐含层，本文采用的变结构网络原理是根据当前状态向量的位置，利用网络节点激活与催眠技术，实现只有激活的节点参与函数逼近，也只有这些节点相应的权值得到了更新[16-17]。首先，设定所有节点处于催眠状态，然后，根据当前状态下基函数的输出值来确定哪些节点被唤醒，哪些节点仍处于催眠状态。即唤醒一个节点则是在网络中加入一个权值继承了以前学习结果的节点。催眠一个节点只是将一个经过学习的节点暂时从网络中删去。这样随着系统状态的转移，活动节点不断变更，使网络节点数一直处于比较小的状态。

3　仿真结果与分析

根据实验测得的稳定平台控制对象数据及对稳定平台的参数辨识，得到稳定平台各模型参数为：ku=3.44 A/V，kE=0.22，kw=5.74 V/rad/s，J=0.025 kg·m2，Ce=0.4，Cm=3.82，R=12.5 Ω，f=0.27。上下盘阀交变摩擦力矩各参数为：R=0.8 m，r0=0.5 m，F=8 N，A0=0.2 m2，η=0.2。RBF神经网络结构选取2-10-2，激活节点阈值为平均权值的10%。Fn取幅值为1～2上的随机信号。

使用Matlab仿真工具，使用上述RBF神经网络自适应滑模变结构控制方法(RBFNeuralNetworkAdaptiveSlidingModeControl，简称RBFASMC)对旋转导向钻井稳定平台控制系统进行仿真，并与一般滑模变结构控制方法(SlidingModeControl，简称SMC)结果进行对比。

3.1正弦信号仿真结果

通过大量仿真实验，使用上述稳定平台模型和上下盘阀交变摩擦模型参数，得到下面的仿真结果(图4—图7)。

图4　工具面角跟踪曲线Fig.4　Tool surface angle tracking curve

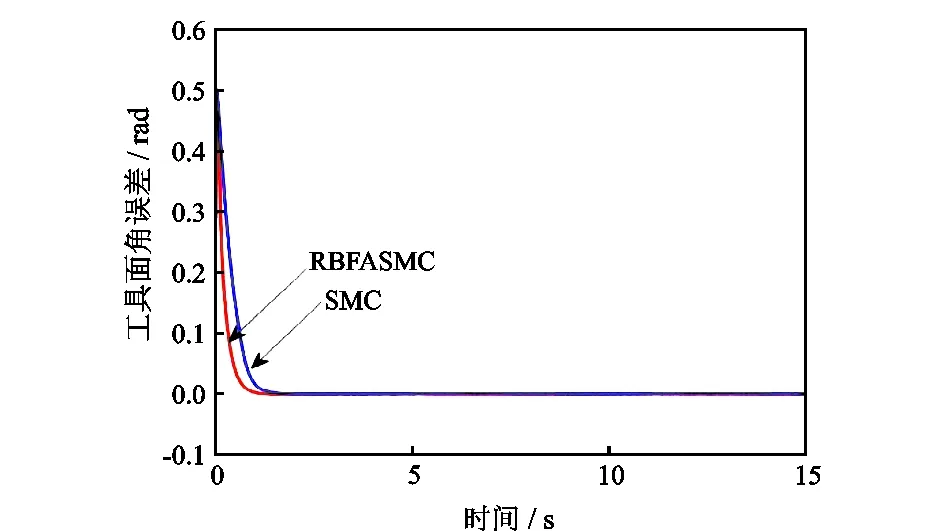
图5　误差曲线Fig.5　Error curve of tool face angle

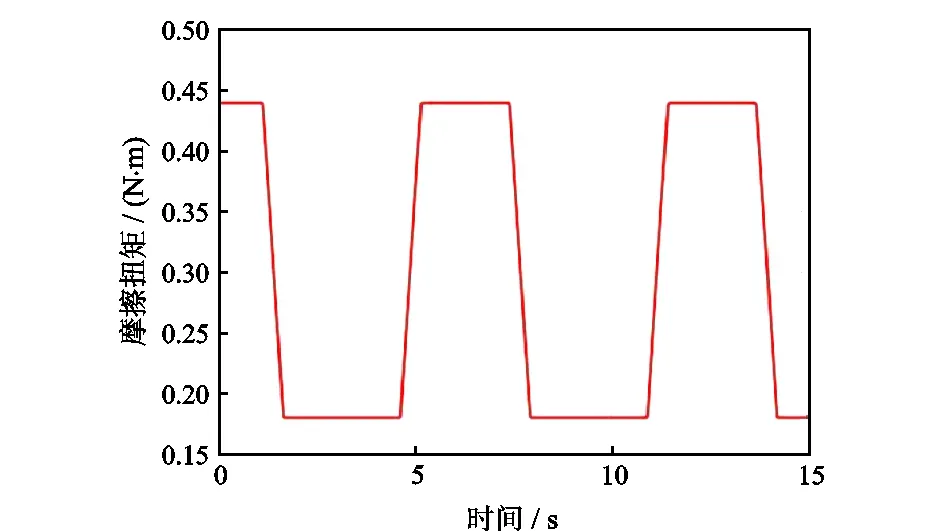
图6　摩擦力矩曲线Fig.6　Friction torque curve

图7　f(x)和b(x)的逼近曲线Fig.7　Approximation curves of f(x) and b(x)

3.2鲁棒性

旋转导向钻井稳定平台在井下工作时,受井下复杂因素影响,造成稳定平台参数的不确定性。例如井下稳定平台转动惯量J受钻井液的冲击会发生变化；井下温度会影响负载电阻R。因此考虑稳定平台参数J和R减少30%时，得到工具面角跟踪曲线和误差曲线，如图8和图9所示。从图中可以看到，在稳定平台参数J和R变化下RBFASMC控制方法依然有良好的跟踪效果，RBF神经网络对稳定平台模型逼近效果良好，而SMC控制方法的跟踪效果明显变差。

图8　J和R减少30%时工具面角跟踪曲线Fig.8　Tool face angle tracking curves when J and R being decreased by 30%

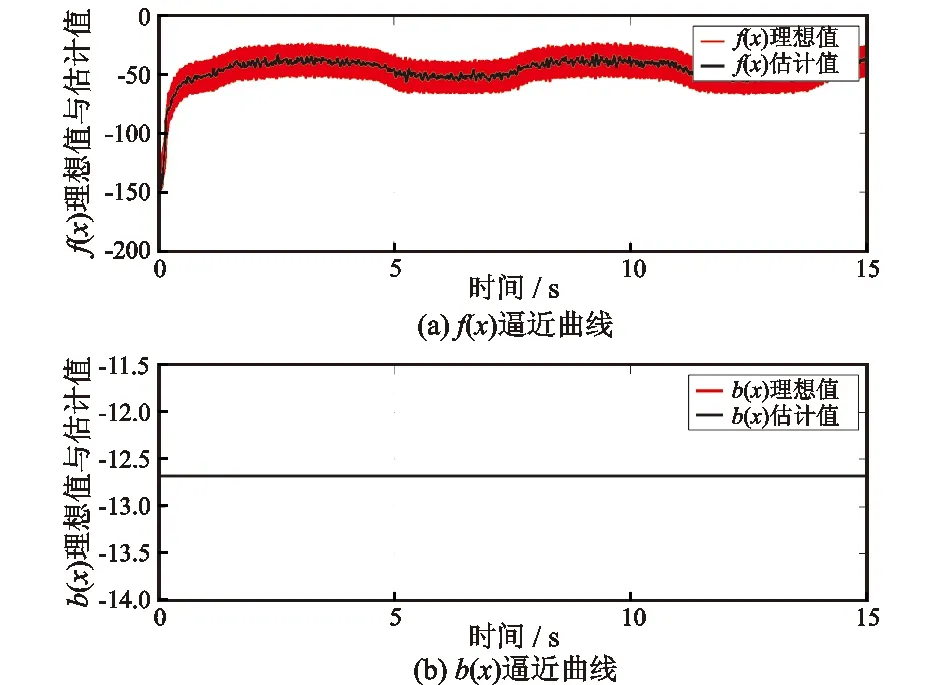
图9　J和R减少30%时f(x)与b(x)逼近曲线Fig.9　Approximation curves of f(x) and b(x) when J and R being decreased by 30%

当未知扰动摩擦Fn幅值变化100%时，得到图10和图11。从图中可以看到，在未知摩擦力矩变化时， RBFASMC控制方法能够有效地克服未知扰动对系统的影响，跟踪和逼近效果依旧良好，而SMC控制方法则无法达到跟踪要求。

图10　扰动摩擦幅值增大100%时工具面角跟踪曲线Fig.10　Tool face angle tracking curves when disturbance friction amplitude increasing twice

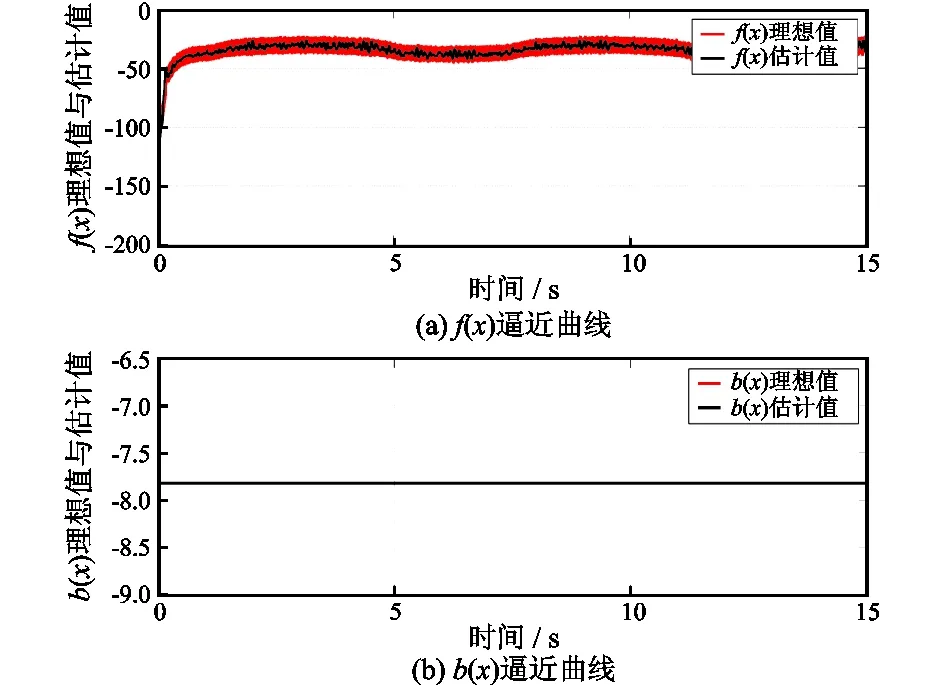
图11　扰动摩擦幅值增大100%时f(x)和b(x)逼近曲线Fig.11　Approximation curves of f(x) and b(x) when disturbance friction amplitude increasing twice

4　结　论

针对稳定平台在井下工作特点，提出一种RBF神经网络自适应滑模变结构控制方法。该方法利用RBF神经网络逼近稳定平台数学模型，通过自适应律调节网络权值，节点激活算法减少网络规模，最后通过滑模变结构方法增强系统鲁棒性。仿真结果表明，该方法能够抑制摩擦力矩对系统产生的不利影响。与一般滑模变结构控制相比，具有良好的鲁棒性和较高的稳定平台姿态控制精度，使控制性能得到了极大的改善。

[1]汪跃龙，王海皎，康思民，等.导向钻井稳定控制平台的反馈线性化控制[J].石油学报，2014,35(5)：952-957.

WANG Yuelong,WANG Haijiao,KANG Simin,et al.Output feedback linearization of servo platform for rotary steering drilling system[J].Acta Petrolei Sinica,2014,35(5):952-957.

[2]FENG Yong,YU Xinghuo,MAN Zhihong.Non-singular terminal sliding mode control of rigid manipulators[J].Automatica,2002,38(12):2159-2167.

[3]霍爱清，贺昱曜，汪跃龙，等.旋转导向钻井工具稳定平台模糊滑模控制研究[J].计算机仿真，2010,27(10)：152-155.

HUO Aiqing,HE Yuyao,WANG Yuelong,et al.Study of fuzzy adaptive sliding mode control for rotary steering drilling stable platform[J].Computer Simulation,2010,27(10):152-155.

[4]曾宪法，张磊，申功璋.基于神经网络的导弹自适应滑模控制器设计[J].系统仿真学报，2008,20(20)：5589-5592.

[5]秦斌，周浩，杜康，等.基于RBF网络的风电机组变桨距滑模控制[J].电工技术学报，2013,28(5)：37-41.

QIN Bin,ZHOU Hao,DU Kang,et al.Sliding mode control of pitch angle based on RBF neural-network[J].Transactions of China Electrotechnical Society,2013,28(5):37-41.

[6]FEI Juntao，YANG Yuzheng，WU Dan.Robust RBF neural network control with adaptive sliding mode compensator for MEMS gyroscope[J].IEEE College of Computer and Information，2013(6):499-504.

[7]郭胜鹏，李东旭，孟云鹤，等.漂浮基空间机器人自适应 RBF 网络终端滑模控制[J].动力学与控制学报，2014,12(4)：53-59.

GUO Shengpeng,LI Dongxu,MENG Yunhe,et al.Adaptive RBF based terminal sliding mode control of free-floating space robots[J].Journal of Dynamics and Control,2014,12(4):53-59.

[8]陈杰，李志平，张国柱.变结构神经网络自适应鲁棒控制[J].自动化学报，2010,36(1)：175-178.

CHEN Jie,LI Zhiping,ZHANG Guozhu.Variable structure neural network adaptive robust control[J].Acta Automatica Sinica,2010,36(1):175-178.

[9]霍爱清，戴晨，汪跃龙，等.增广非最小状态空间法的稳定平台预测控制研究[J].计算机工程与应用，2013,49(17)：239-244.

HUO Aiqing,DAI Chen,WANG Yuelong,et al.Predictive control in stabilized platform based on augmented non-minimal state-space method[J].Computer Engineering and Applications,2013,49(17):239-244.

[10] 闫文辉，彭勇，张绍槐.旋转导向钻井工具的研制原理[J].石油学报，2005,26(5)：94-97.

[11] 汪跃龙，张璐，汤楠，等.旋转导向钻井惯导平台动力学分析与运动研究[J].机械工程学报，2012,48(17)：65-69.

WANG Yuelong,ZHANG Lu,TANG Nan,et al.Dynamics and rotational movement analysis of servo platform for rotary steerable drilling system[J].Journal of Mechanical Engineering,2012,48(17):65-69.

[12] 童克文，张兴，张昱，等.基于新型趋近律的永磁同步电动机滑模变结构控制[J].中国电机工程学报，2008,28(21)：102-106.

TONG Kewen,ZHANG Xing,ZHANG Yu,et al.Sliding mode variable structure control of permanent magnet synchronous machine based on a novel reaching law[J].Proceedings of the CSEE,2008,28(21):102-106.

[13] WANG Lianyong,CHAI Tianyou,ZHAI Lianfei.Neural-network-based terminal sliding-mode control of robotic manipulators including actuator dynamics[J].IEEE Transactions on Industrial Electronics,2009,56(9):3296-3304.

[14] 乔俊飞，韩红桂.RBF神经网络的结构动态优化设计[J].自动化学报，2010,36(6)：865-872.

QIAO Junfei,HAN Honggui.Optimal structure design for RBFNN structure[J].Acta Automatica Sinica,2010,36(6):865-872.

[15] HUANG Deshuang,DU Jixiang.A constructive hybrid structure optimization methodology for radial basis probabilistic neural networks[J].IEEE Transactions on Neural Networks / a Publication of the IEEE Neural Networks Council,2008,19(12):2099-2115.

[16] 楼顺天，雷虎民，陈新海.一种新型动态RBF网络自适应控制器[J].西北工业大学学报，1999,17(1)：103-107.

[17] HUANG Guangbin,CHEN Lei,Siew C K.Universal approximation using incremental constructive feedforward networks with random hidden nodes[J].IEEE Transactions on Neural Networks / a Publication of the IEEE Neural Networks Council,2006,17(4):879-892.

责任编辑：董瑾

Sliding Mode Variable Structure Control of Stabilized Platform in Rotary Steerable Drilling System Based on RBF Neural Network

HUO Aiqing,QIU Long,WANG Yuelong

(College of Electronic Engineering,Xi'an Shiyou University,Xi'an 710065,Shaanxi,China)

Aiming at the uncertainty of the stabilized platform in rotary steerable drilling system caused by friction,an adaptive variable structure control method based on RBF neural network is proposed to improve the accuracy and the anti-interference ability in the control of the stabilized platform.RBF neural network is used for approximating the uncertainty of the control model of the stabilized platform,the size of the RBF neural network is reduced by designing the wake-up and activation threshold of RBF network nodes,and the system robustness is increased by the adaptive law with adjustable weights and sliding mode control.The simulated result using general sliding mode variable structure control method is compared with that using the sliding mode variable structure control method based on RBF neural network,and it is shown that,the sliding mode variable structure control method based on RBF neural network can effectively approximate the control object model and has strong robustness.

control of stabilized platform in rotary steerable drilling system;RBF neural network;sliding mode variable structure;node activating

A

2015-09-14

陕西省科学技术研究发展计划项目“导向钻井惯导稳定平台控制系统的关键技术研究”(编号：2013K07-16)

霍爱清(1966-)，女，教授，主要从事自动控制和计算机工业控制等方面的研究。E-mail:aqhuo@xsyu.edu.cn

10.3969/j.issn.1673-064X.2016.04.018

TE242；TP273

1673-064X(2016)04-0103-06