非均质碳酸盐岩油藏油水两相流动模拟

吕心瑞，黄朝琴，赵娟

(1.中国石化 石油勘探开发研究院，北京 100083；2.中国石油大学(华东) 石油工程学院，山东 青岛 266555；3.中海油 研究总院，北京 100029)



非均质碳酸盐岩油藏油水两相流动模拟

吕心瑞1，黄朝琴2，赵娟3

(1.中国石化 石油勘探开发研究院，北京 100083；2.中国石油大学(华东) 石油工程学院，山东 青岛 266555；3.中海油 研究总院，北京 100029)

为了模拟考虑非均匀基质情况下裂缝的特殊导流作用，采用离散裂缝模型结合有限体积方法进行多裂缝非均质碳酸盐岩油藏两相流动模拟研究，对裂缝显式降维处理，根据基质岩块非均质特征分区划分Delaunay三角网，以此为基础构建非均匀控制单元，采用有限体积法推导其数值计算格式，并基于IMPES方法进行求解。该方法避免了由于介质交界面处渗透率变化较大、利用标准有限体积方法产生不准确速度场的问题，实现了非均质碳酸盐岩油藏油-水两相流动模拟。最后通过算例验证了该方法的正确性，并开展了含复杂裂缝非均匀基质碳酸盐岩油藏水驱数值模拟研究，为此类油藏的开采提供参考依据。

非均质碳酸盐岩油藏；离散裂缝模型；有限体积法；两相流动；数值模拟

吕心瑞，黄朝琴，赵娟.非均质碳酸盐岩油藏油水两相流动模拟[J].西安石油大学学报(自然科学版)，2016，31(4):75-81.

LYU Xinrui,HUANG Zhaoqin,ZHAO Juan.Numerical simulation of water flooding development of heterogeneity carbonate reservoir[J].Journal of Xi'an Shiyou University (Natural Science Edition),2016,31(4):75-81.

引　言

碳酸盐岩油气藏分布广泛、类型多样，其油、气储量分别占世界油、气总储量的48%和28%，油、气产量分别约占世界油、气总产量的60%和30%[1]。碳酸盐岩油藏分布最为广泛的类型主要为孔隙(溶洞)型、混合(裂缝-孔隙)型和裂缝型[2]。与常规陆源碎屑岩油藏相比，其岩性复杂，岩相变化大，储集空间类型多样，多数含有不同尺度的裂缝，基质由溶孔、溶洞、孔隙等组成，非均质性强，这些因素造成此类油藏复杂的渗流机理和相对较低的采收率。目前，此类油藏商业化数值模拟软件多采用连续性介质模型，但均存在不同的缺点[3-7]，难以精确描述裂缝的特殊导流作用，且并非所有类型都可等效为连续性介质，其表征单元体的大小及等效渗透系数的确定也都存在一定困难。近年来，诸多学者应用离散裂缝模型对此类强非均质性油藏进行数值模拟研究，基于多种数值计算方法对模型进行了离散求解，在考虑绝对渗透率非均质性和单相流的各向异性等方面取得一定进展[8-13]。但由于非均质介质交界面处渗透率变化较大，存在着利用标准控制体积方法会产生不准确速度场的问题。

因此，为了获取精确的速度场，准确刻画裂缝的特殊导流作用，同时考虑基质岩块非均质特征，本文基于离散裂缝模型建立相应的油-水两相流动数学模型，在整个研究区域，同时考虑降维裂缝及非均匀基质的影响，分区划分Delaunay三角网，构建非均匀控制体积单元，应用有限体积法建立其数值计算格式，并采用IMPES方法进行求解。通过算例验证本方法的正确性，以此为基础开展含复杂裂缝非均匀基质碳酸盐岩油藏注水开发模拟，分析裂缝的存在及基质非均质性对油藏开发效果的影响。

1　离散裂缝数学模型

根据离散裂缝模型原理[9]，裂缝中流体流动符合N-S方程，通过立方定律可得到裂缝的等效渗透率及沿裂缝开度方向的渗流速度分布，且等效后的流动参数及相关物理量沿裂缝开度方向不变，据此可对裂缝以等效达西定律的形式进行降维处理。分别建立基质岩块和裂缝中油-水两相流动控制方程，利用叠加原理将基质岩块与裂缝的流动控制方程进行叠加。由于基质岩块的非均质性引起含水饱和度不连续，据此建立二者饱和度关系表达式，构建离散裂缝模型的油水两相数学模型。

考虑油藏中不可压缩油-水两相流动，其流动控制方程包括质量守恒方程、Darcy定律、饱和度方程和毛管压力关系等，具体如下：

(1)质量守恒方程

根据质量守恒原理分别建立油水两相的连续性方程，对于油相：

(1)

对于水相：

(2)

(2)运动方程

当油藏中流体渗流服从Darcy定律时，渗流速度的矢量表达式为：

油相

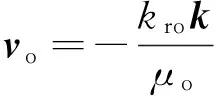
(3)

水相

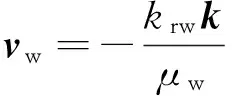
(4)

其中：μi为流体黏度，Pa·s；pi为流体压力，Pa；g为重力加速度，m/s2；z为由某一基准面算起的垂直深度坐标，向上为正，m；kri为相对渗透率；k为渗透率张量，在各向同性地层中可以用标量k表示，m2。

(3)辅助方程

饱和度方程：So+Sw=1。

(5)

毛管压力方程：po-pw=pc(Sw)。

(6)

其中，pc为毛管压力，Pa。

将上述油水两相的运动方程分别带入各自的连续性方程，利用复合求导法进行化简，建立描述油藏中油水两相不可压缩流体非混相驱替的标准控制方程，对于油相，

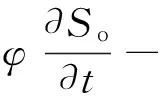
V Theory of toothpaste raw material (To be continued) 2 58

(7)

对于水相，

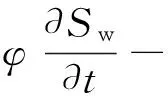
(8)

其中，qi=Qi/ρi，i={o,w}，表示单位时间内流入或流出的体积流量。

定义上述方程中各相的流度

(9)

这样，各向同性均质地层中用渗透率标量k来代替渗透率张量。油水两相不可压缩流体非混相流动，在不考虑重力情况下的控制方程为：

对于油相

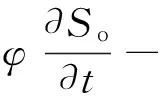
(10)

对于水相

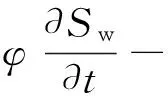
(11)

将上面描述油相和水相的控制方程式(10)和式(11)相加，并保留水相控制方程，结合两个辅助方程，可将上述数学模型转化为偏微分方程

(12)

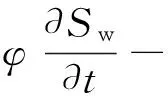
(13)

式(12)称为流动压力方程，式(13)称为饱和度方程。

数学模型的初始条件为：

pi(x,0)=pi(x)，Si(x,0)=Si(x)，i={w,o}。

(14)

边界条件可以为各种形式的Dirichlet边界条件、Neumann边界条件以及二者的混合形式。

Dirichlet边界条件为：

pi(x,t)=pi，Si(x,t)=Si，i={w,o}。

(15)

Neumann边界条件，本文假设油藏的边界为不渗透边界，即

vi·n=-(λipi)·n=0，Si·n=0，i={w,o}。

(16)

以上即为油藏中不可压缩油-水两相非混相流动的数学模型。

在上述二维离散裂缝模型中，二维基质岩块区域控制方程系统为：

(17)

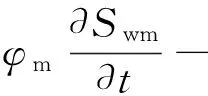
(18)

一维裂缝区域控制方程系统为：

(19)

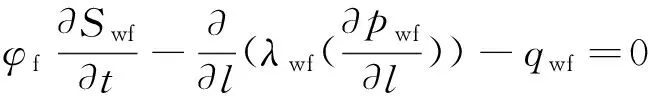
(20)

这里，l表示沿裂缝方向的坐标系。

利用f来代表压力方程和饱和度方程系统，在单孔隙介质模型中，整体形式方程的积分可以写为

∫ΩfdΩ=∫ΩmfmdΩm+∫ΩfffdΩf=0，

(21)

(22)

这样建立了油-水两相离散裂缝模型流动方程，理论上离散裂缝模型可以用于任意复杂形状的裂缝性多孔介质。相比于单孔隙介质模型，离散裂缝模型在裂缝内的积分大大简化了问题。为了使积分形式保持一致性，裂缝开度e作为系数出现在一维积分形式前面。

在对方程(22)中非线性项线性化以及对时间和空间离散化后，可得到系统的离散化方程

∫ΩfdΩ=Amxm-bm+Afxf-bf=0。

(23)

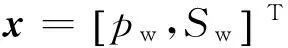
在基质岩块-裂缝交界面处，由于没有流体质量的变化，因此通过交界面的各相流量及法向速度是连续的，即

qif*=qm*i;vim·nmf=vim·nfm,i={w,o}。

(24)

其中，nmf是边界上的法向向量。由于在离散裂缝模型中利用叠加原理把流动方程整合在一起，当把基质岩块和裂缝的流动方程加在一起时这些项被消去，因此在流动方程中可以忽略基质岩块和裂缝交界面处的流量。

基质岩块-裂缝交界面处任意给定点的pim=pif。这里，i={w,o}。由式(13)可知毛管压力也相等，即

pcm(Swm)=pcf(Swf)。

(25)

图1　不同介质交界面处毛管压力Fig.1　Capillary pressure in the interface of different media

因此，利用毛管压力的连续性假设条件，在基质岩块-裂缝交界面处建立Swm与Swf之间的物理关系

(26)

利用式(24)和复合求导法则，裂缝中饱和度方程可以应用基质岩块含水饱和度Swm表达为

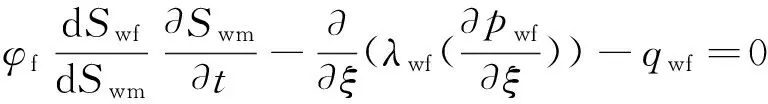
(27)

根据xm=xf=x的假设，仅当基质岩块和裂缝中毛管压力函数相同时，也就是dSwf/dSwm=1时适用。因此，对于不同的基质岩块和裂缝毛管压力表达式，需要计算相应的dSwf/dSwm。

2　非均质基质岩块离散裂缝模型数值计算格式

基于有限体积方法对压力方程和饱和度方程进行空间离散，首先对方程在一个控制体积单元上进行积分，控制体单元即为二维Delaunay三角形或三维四面体的重心与各边中点连线所构成的对偶网格。图2(a)为常规考虑均质基质岩块的裂缝性多孔介质控制体积单元示意图，其离散裂缝模型不可压缩油-水两相数值计算格式在文献[8]中已建立，本文考虑含裂缝非均质基质岩块多孔介质控制体积单元，如图2(b)所示示意图，建立其不可压缩油-水两相数值计算格式。

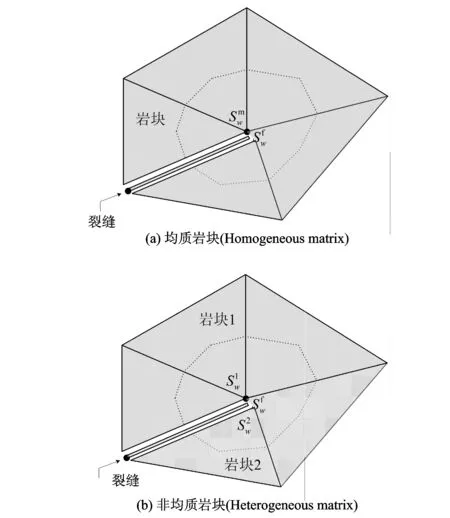
图2　含有裂缝的控制体积单元Fig.2　Control volume unit containing a fracture

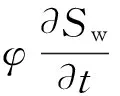
如图2(b)所示，在一个控制体单元内，存在1条裂缝和2种不同的基质岩块，考虑不同基质岩块间毛管压力连续，可建立非均质基质岩块间饱和度的关系，即

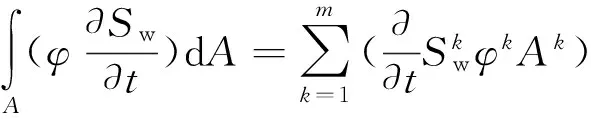
(28)

(29)

这里上角标k=1，…，nm是控制体内不同介质的指数。基于毛管力连续概念，可以建立不同介质饱和度的关系。此处以方程(29)中Bk最大值为参考介质。

根据方程(18)和复合求导法则可以得到

(30)

源汇项的积分可以写为

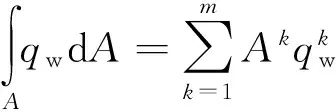
(31)

散度项的积分可以依照式

(32)

来确定，控制体单元包含的每个三角形都是局部均质的，不同介质间饱和度可以通过方程(26)进行关联计算。

其中N表示边界单元的个数，将式(30)、(31)、(32)结合在一起即得到流动压力方程和饱和度方程的数值计算格式，即

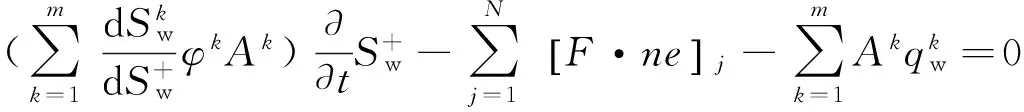
(33)

因此，基于控制体积方法建立了式(33)所示的考虑基质岩块非均质性的离散裂缝模型流动方程的数值计算格式。

3　算例分析

3.1正确性验证

为了验证上述理论与方法的正确性，建立单裂缝多孔介质注水模型，分别基于离散裂缝模型和单孔隙介质模型进行数值模拟，并对模拟结果进行对比分析。本文采用文献[8]中基础物理模型，模型尺寸、裂缝参数及流体物性均与之相同。但此处基质岩块为非均质多孔介质，如图3所示，基质岩块平分为4个区域，相邻基岩块物性不同，物性分布如表1所示。

以含θ=45°裂缝的物理模型为例，首先将研究区域划分为Delaunay三角网，然后构建有限体积控制单元。图4为网格划分结果，以油藏边界、裂缝及不同基质岩块区域边界作为网格划分边界，实现了不同区域非均匀网格划分，共得到2704个控制体单元节点。以单孔隙介质模型计算结果作为参考，将基于本文方法流动模拟计算结果与之对比，如图5所示，可以看出二者具有较好一致性，从而验证本文方法正确性。

图3　单裂缝多孔介质几何模型Fig.3　Geometrical configuration of the porous media with a fracture

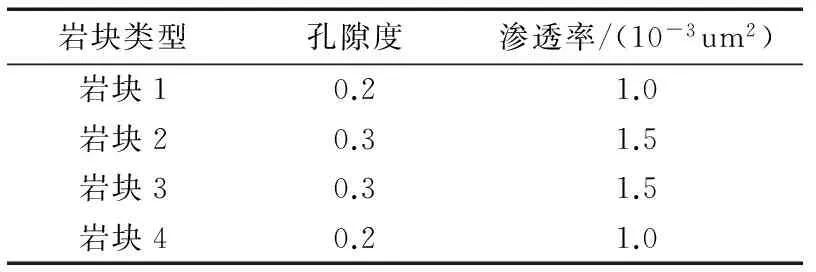
岩块类型孔隙度渗透率/(10-3um2)岩块10.21.0岩块20.31.5岩块30.31.5岩块40.21.0

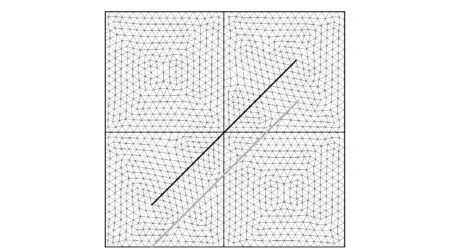
图4　物理模型网格划分示意图Fig.4　Grid division of the physical model with a fracture

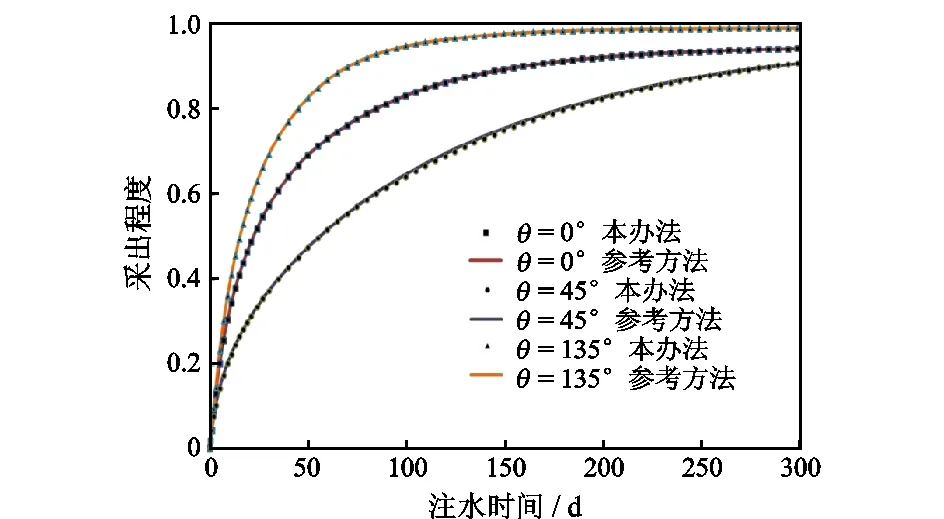
图5　基于2种模型的油相采出程度对比Fig.5　Oil recovery percent comparison of fractured media based on two models

同时，基于本方法得到的控制体积单元节点远小于基于单孔隙介质模型得到的28 773个单元节点，计算效率显著提高，说明了本方法的高效性。此外，从计算结果发现基质岩块的非均质特征对油藏的采出程度也产生了影响，在相同开采条件下，非均匀基质岩块油藏比均匀基质岩块油藏最终采出程度小1.3%。

3.2复杂裂缝油藏注水开发模拟

基于本文方法，开展复杂裂缝油藏注水开发模拟，考虑图6所示的1/4五点井网注水模型，油藏规模为300 m×300 m，厚度为10 m，基质岩块物性分布见表2，油藏中含有3条裂缝，各条裂缝起始坐标分别为(30,150)、(240,225)，(125,30)、(200,275)和(50,100)、(250,50)。油水的物性参数以及裂缝参数与算例3.1中一致；束缚水饱和度为0.2，残余油饱和度为0.2，基质岩块和裂缝的水相相对渗透率krw=Se2，油相相对渗透率kro=(1-Se)2，

图6　含复杂裂缝的二维油藏模型示意图Fig6　Schematic of 2D reservoir model with complex fractures

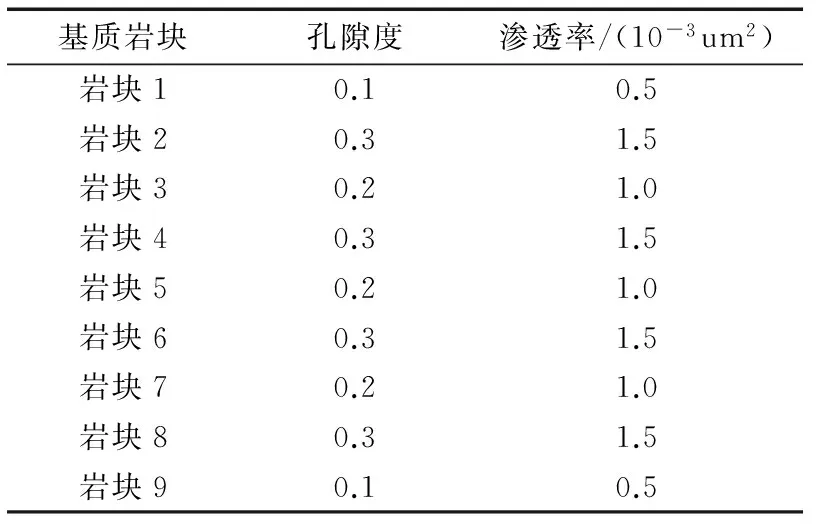
基质岩块孔隙度渗透率/(10-3um2)岩块10.10.5岩块20.31.5岩块30.21.0岩块40.31.5岩块50.21.0岩块60.31.5岩块70.21.0岩块80.31.5岩块90.10.5

其中Se=(Sw-Swr)/(1-Swr-Sor)；初始油藏压力为10MPa，初始含水饱和度为0.2，忽略毛管力和重力的影响，注入端和采出端的速度均为30m3/d。

对复杂裂缝性油藏物理模型进行Delaunay三角形网格划分，离散结果共得到3 377个控制体单元节点，基于此网格系统构建有限体积数值计算控制单元。通过本文理论方法，数值计算可得复杂裂缝性油藏模型中各时刻含水饱和度分布情况，图7分别为150 d、300 d、600 d、1 200 d、2 400 d、4 800 d时油藏中含水饱和度分布。可以看出随着油井的生产，油藏压力逐渐降低，由于裂缝具有较大的渗透率，裂缝对油藏中流体流动产生了很大的影响，注入水沿裂缝大量窜进，沿着裂缝方向的水驱油速度相对于基质岩块大大加快，裂缝中的含水饱和度迅速增大。不同区域基质岩块由于物性的差异，使得基质岩块中水驱油速度和含水饱和度也有差异，造成了其注水开发的复杂性。

图7　不同时刻含水饱和度分布剖面Fig.7　Water saturation profiles at different times

图8(a)为含复杂裂缝非均质油藏与均质油藏采出程度随时间的变化曲线；图8(b)为复杂裂缝性非均质油藏与均质油藏油井含水率随时间的变化曲线。从图中可以看出：裂缝及基质岩块非均质性的存在使得油藏采出程度变小，油井见水时间提前，且采油速度变慢，不利于油藏的开采。因此，正确认识裂缝的分布和基岩非均质状况对注水开发效果评价及注采井网的布置有非常重要的意义。

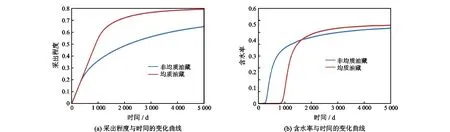
图8　复杂非均质性对油藏采出程度和油井含水率影响Fig.8　Effect of reservoir heterogeneity on recovery percent of oil reservoir and water cut of oil well

4　结　论

(1)建立了可用于含裂缝非均质碳酸盐岩油藏两相流流动模拟的方法，采用离散裂缝模型结合有限体积方法较好地描述了裂缝的特殊导流作用及基质岩块非均质特征，并通过算例验证了方法的正确性及高效性。

(2)该方法对整体研究区分区域划分Delaunay三角网，并在此基础上构建非均匀控制单元，建立了考虑非均匀基质岩块的有限体积数值计算格式，避免了由于不同物性介质交界面处渗透率变化较大、利用标准有限体积方法会产生不准确速度场。

(3)该方法可用于非均质碳酸盐岩油藏数值模拟，尤其适应于含有裂缝且基质岩块非均质性较强的复杂油藏。文中仅对二维两相问题予以研究，对于多相、三维问题有待深入研究。

[1]柏松章.碳酸盐岩潜山油田开发[M].北京：石油工业出版社，1996，5.

[2]苏尔古乔夫.碳酸盐岩油藏的开采[M].北京：石油工业出版社，1994,1.

[3]BARENBLATT G I,ZHELTOV I P,KOCHINA I N.Basic concept in the theory of homogeneous liquids in fissured rocks[J].J Appl Math Mech,1960,24(5):1286-1303.

[4]WARREN J E,ROOT P J.The behavior of naturally fractured reservoirs[J].SPE J,1963,3(3):245-255.

[5]Ghorayeb K,Firoozabadi A.Numerical study of natural convection and diffusion in fractured porous media[J].SPE J,2000,40(1):12-20.

[6]THOMAS L K,DIXON T.PIERSON R G.Fractured reservoir simulation[J].SPE J,1983,23(1):42-54.

[7]姚军，王子胜.缝洞型碳酸盐岩油藏试井解释理论与方法[M].东营:中国石油大学出版社，2007:157-172.

[8]吕心瑞,姚军，黄朝琴，等.基于有限体积法的离散裂缝模型两相流动模拟[J].西南石油大学学报(自然科学版),2012,34(6):123-130.

[9]黄朝琴，姚军,王月英，等.基于离散裂缝模型的裂缝性油藏注水开发数值模拟[J].计算物理,2011,28(1):41-49.

HUANG Zhaoqin,YAO Jun,WANG Yueying,et al.Numerical simulation on water flooding development of fractured reservoirs in a discrete-fracture model[J].Chinese Journal of Computational Physics,2011,28(1):41-49.

[10] KIM J G,DEO M D.Finite elements，discrete fracture model for multiphase flow in porous media[J].AIChE Journal,2000,46(6):1120-1130.

[11] 姚军，黄涛，黄朝琴.非均匀低渗透油藏非线性流动数值模拟[J].计算物理，2014,31(5):552-558.

YAO Jun,HUANG Tao,HUANG Zhaoqin.Numerical simulation of nonlinear flow in heterogeneous and low-permeability reservoir[J].Chinese Journal of Computational Physics,2014,31(5):552-558.

[12] KARIMI Fard M,FIROOZABADI A.Numerical simulation of water injection in fractured media using discrete-fracture model and the Galerkin method[J].SPE Reservoir Evaluation & Engineering,2003,6(2):117-126.

[13] 严侠，黄朝琴，姚军，等.基于模拟有限差分的嵌入式离散裂缝数学模型[J].中国科学：技术科学，2014，44(12)：1333-1342.

YAN Xia,HUANG Zhaoqin,YAO Jun,et al.The embeded discrete fracture model based on mimetic finite difference method[J].Sci Sin Tech,2014,44:1333-1342.

责任编辑：贺元旦

Numerical Simulation of Water Flooding Development of Heterogeneous Carbonate Reservoir

LYU Xinrui1,HUANG Zhaoqin2,ZHAO Juan3

(1.Research Institute of Petroleum Exploration and Development,SINOPEC,Beijing 100083,China;2.Faculty of Petroleum Engineering,China University of Petroleum (East China),Qingdao 266555,Shandong,China;3.Research Institute,CNOOC,Beijing 100029,China)

Most carbonate reservoir contains multi-scale fractures,and carbonate matrix has strong heterogeneity.In order to accurately describe the special flow guiding effect of the fractures in the heterogeneous matrix,the two-phase flow in the water flooding process of the heterogeneous carbonate reservoir with multi-scale fractures was simulated using finite volume method based on discrete fracture model.The model simplifies fracture by using (n-1)-dimensional cells in a n-dimensional domain,meanwhile the heterogeneity of matrix is considered.Delaunay triangulation subdivision is used in the whole research area,and then the inhomogeneous control volume cells are constructed based on the Delaunay triangulation.The numerical computational scheme is derived based on the finite volume method,and the equations are solved by IMPES method.The method avoids producing the inaccurate velocity field because of the great permeability change in the interface between different media using standard finite volume method.So the numerical simulation of the two-phase flow in the water flooding process of the heterogeneous carbonate reservoir is realized.At last the correctness of the theory and algorithm of the method is verified through examples.The numerical simulation of heterogeneous carbonate reservoir based on this method provides the reference for the development of this kind of reservoirs.

heterogeneous carbonate reservoir;discrete fracture model;finite volume method;two-phase flow;numerical simulation

A

2016-03-10

国家科技重大专项“碳酸盐岩油田开发关键技术”(编号：2011ZX05014)

吕心瑞(1983-)，男，主要从事油气田开发相关研究。E-mail:lvxr.syky@sinopec.com

10.3969/j.issn.1673-064X.2016.04.013

TE319

1673-064X(2016)04-0075-07