六自由度柔性关节机械臂的动力学分析

王　海　付邦晨,2　薛　彬　杨春来

1.安徽工程大学，芜湖，2410002.芜湖安普机器人产业技术研究院有限公司，芜湖，241000



六自由度柔性关节机械臂的动力学分析

王海1付邦晨1,2薛彬1杨春来1

1.安徽工程大学，芜湖，2410002.芜湖安普机器人产业技术研究院有限公司，芜湖，241000

大多数的机器人都是在刚体动力学假设的基础上进行运动控制设计的，因此其在实际操作中的精度和效率受到一定的限制，而柔性机械臂可以很好地解决此类问题。首先给出了六自由度的柔性关节机械臂的简化模型，利用拉格朗日方法建立其动力学方程；然后以单自由度柔性关节机械臂为例，基于神经网络反演法对其控制率进行了设计；最后基于Simulink验证了控制器设计的有效性。

六自由度；柔性关节；动力学；拉格朗日方程；神经网络反演法

0　引言

柔性关节机械臂相比于刚性机械臂具有高度非线性、强耦合的特点[1]。随着机器人技术的快速发展，Lagrange法(功能平衡法)、Newton-Euler法(动态平衡法)和Kane法等已用于对机械臂动力学的研究[2]。有学者采用Kane方法对柔性机械臂动力学进行研究，但计算过程较为繁琐，且多自由度系统的建模太为复杂[3]。本文主要基于Lagrange法，以能量的方式搭建柔性关节机械臂动力学模型[4]，避免了计算复杂的约束力。

1　六自由度柔性关节机械臂动力学建模

柔性机械臂主要分为柔性杆机械臂和柔性关节机械臂两类[5]。由于柔性杆机械臂的模型建立较为复杂，且其柔性对运动性能影响较小[6]，因此忽略杆的柔性，将研究对象简化为柔性关节机械臂。柔性关节机械臂的柔性主要由谐波减速器和力矩传感器产生，可以利用Spong提出的假设采用线性弹簧来描述柔性关节特性[7]。

运用Lagrange法推导柔性机械臂的动力学方程前，需先得到各个电机转子、连杆及关节的动能和势能表达式。n关节柔性机械臂的总能量由连杆和电机转子的动能以及连杆、电机(包含减速器)重力势能和柔性关节势能构成[8]。简化为线性弹簧的柔性关节的弹性势能可表示为

式中，Ki为关节i的刚度；θi为电机i端的角位移；qi为关节i的连杆端角位移。

为了便于模型推导，建立六自由度柔性关节机械臂的简化模型，如图1所示。定义相关符号的含义：N为传动比，即输入速度与输出速度之比；Jmi为第i个电机转子的转动惯量，i=1，2，…，6；Ili为第i个连杆的转动惯量；mli为第i个连杆的质量；mri为第i个电机转子的质量；θmi为电机经过减速前的角度，θmi= Nθi； di、li分别为第i个连杆的质心距离和连杆长。

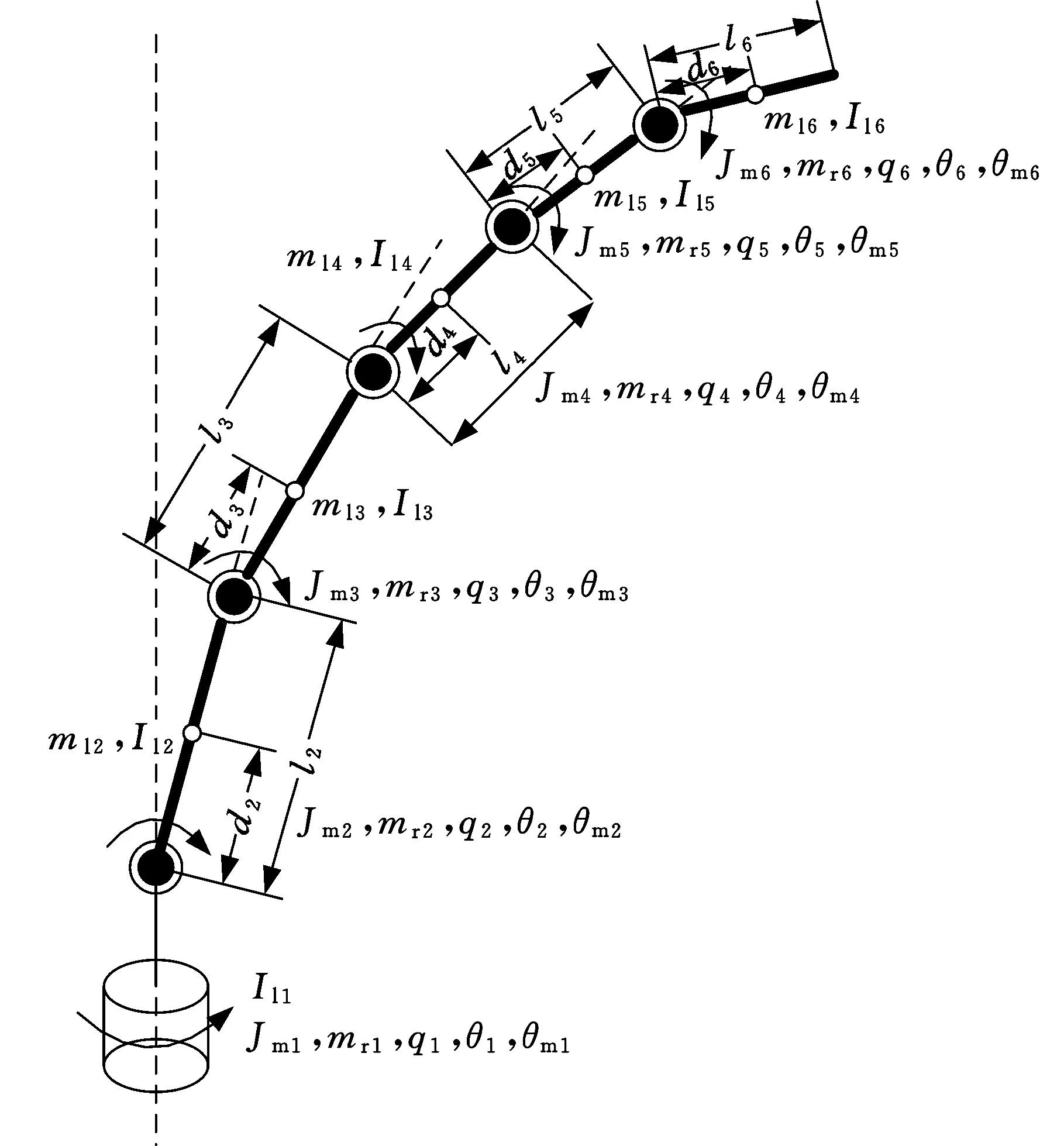
图1　6-DOF柔性关节机械臂简化模型

利用Lagrange法对图1所示的简化模型进行动力学方程推导，依次得到6个电机转子和连杆的动能：

(1)电机1转子动能

(1)

(2)连杆1的动能

(2)

(3)电机2转子动能

(3)

(4)连杆2的动能

(4)

s2=sinq2

(5)电机3转子的动能

(5)

(6)连杆3的动能

(6)

(7)电机4转子动能

(7)

(8)连杆4的动能

(8)

c3-4=cos(q3+q4)

(9)电机5转子动能

(9)

c4=cosq4

(10)连杆5的动能

(10)

c3-5=cos(q3+q4+q5)c4-5=cos(q4+q5)

c5=cosq5

(11)电机6转子动能

(11)

(12)连杆6的动能

Tl6={ml6[(l2s2+l3s2-3+l4s2-4+l5s2-5+

(12)

s2-6=sin(q2+q3+q4+q5+q6)

s3-6=sin(q3+q4+q5+q6)

c4-6=cos(q4+q5+q6)

c5-6=cos(q5+q6)c6=cosq6

因此机械臂系统的总动能为

(13)

机械臂总的弹性势能为

(14)

机械臂总的重力势能为

Pg=g[ml2d2c2+mr3l2c2+ml3(l2c2+d3c2-3)+

mr4(l2c2+l3c2-3)+ml4(l2c2+l3c2-3+d4c2-4)+

mr5(l2c2+l3c2-3+l4c2-4)+ml5(l2c2+l3c2-3+

l4c2-4+d5c2-5)+mr6(l2c2+l3c2-3+l4c2-4+l5c2-5)+

ml6(l2c2+l3c2-3+l4c2-4+l5c2-5+d6c2-6)]

(15)

将上面得到的各个能量方程代入Lagrange方程，忽略阻尼影响时，可认为阻尼矩阵为零矩阵，因此得到简化的柔性机械臂模型：

(16)

2　数值仿真

选取单连杆柔性关节机械臂为研究对象，如图2所示，其动力学方程为[9]

(17)

其中，q为连杆转动角度；θ为电机的转动角度；I、J分别为连杆和电机的转动惯量；mglsinq为连杆的重力矩；l为连杆长度；K为关节刚度；τm为控制输入。

图2　单连杆柔性关节机械臂示意图

(18)

为了达成不需要建立模型的柔性机械臂反演控制的目标，将式(18)改写为

(19)

g(x)=-x3-[mglsinx1+K(x1-x3)]/I

f(x)=K(x1-x3)/Jm=1/J

式中，x为系统的状态，x=[x1x2x3x4]T。

2.1基本反演控制器的设计

利用反步法逐步设计位置控制器，主要分以下几个步骤进行：

(1)定义e1=x1-x1d，取x1d=yd为位置指令，则e1对时间求导可得：

(20)

定义e2=x2-x2d，其中，x2d为虚拟控制量，取

(21)

则由式(20)、式(21)得：

-k1e1+e2

(22)

(2)e2对时间求导得

(23)

取e3=x3-x3d，则虚拟控制量为

(24)

(25)

由式(23)、式(24)得

(26)

设计Lyapunov函数为

(27)

则

(3)e3对时间求导得

(28)

由式(23)～式(25)、式(27)得

(29)

(30)

(31)

(32)

(33)

(34)

设计Lyapunov函数为

(35)

(36)

(4)将控制输入信号引入设计中，实现控制系统的稳定。由已知得：

(37)

则由式(28)、式(30)、式(31)、式(33)得

(38)

(39)

控制律设计为

(40)

将式(40)代入式(39)得

(41)

设计Lyapunov函数为

则

(42)

2.2神经网络反演控制器的设计

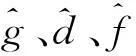
(43)

其中，Wi为理想权值，i=1，2，3；φi为高斯基函数，‖ξ‖=‖[ξ1ξ2ξ3]T‖ <ξN，‖Wi‖≤WM，ξN为网络训练时设定的权值范围，WM为网络训练时设定的阈值。定义

(44)

定义

‖Z‖F≤ZM

(45)

(46)

设计Lyapunov函数

V4=ξTξ/2η>0

神经网络权值的自适应律设计为

(47)

Φ=[0φ1φ2φ3]T

(48)

2.3基于Simulink的神经网络反演控制器的仿真

为了检验上述算法的合理性，我们以单连杆柔性关节机械臂为例，在Simulink中对其进行仿真，其动力学方程为式(17)，实际参数为mgl=6.9 N·m，I=2.1×10-3kg·m2，J=3.26×10-1kg·m2，K=8 N·m。位置指令yd=sint，初始位置x(0)=0，控制器参数为k1=k2=k3=k4=5。采用BRF神经网络逼近g、d和f，控制律为式(40)，自适应律为式(47)、式(48)，神经网络的输入x=[x1x2x3x4]T。在自适应律中，取n=0.01，Γ2=Γ3=Γ4=250，即Q=diag(0，0.004，0.004，0.004)，m=1.0。图3为系统Simulink仿真图。图4所示为指关节的位置跟踪曲线，图5所示为关节的控制输入力矩，图6所示为g(x)的实际值及其估计值。

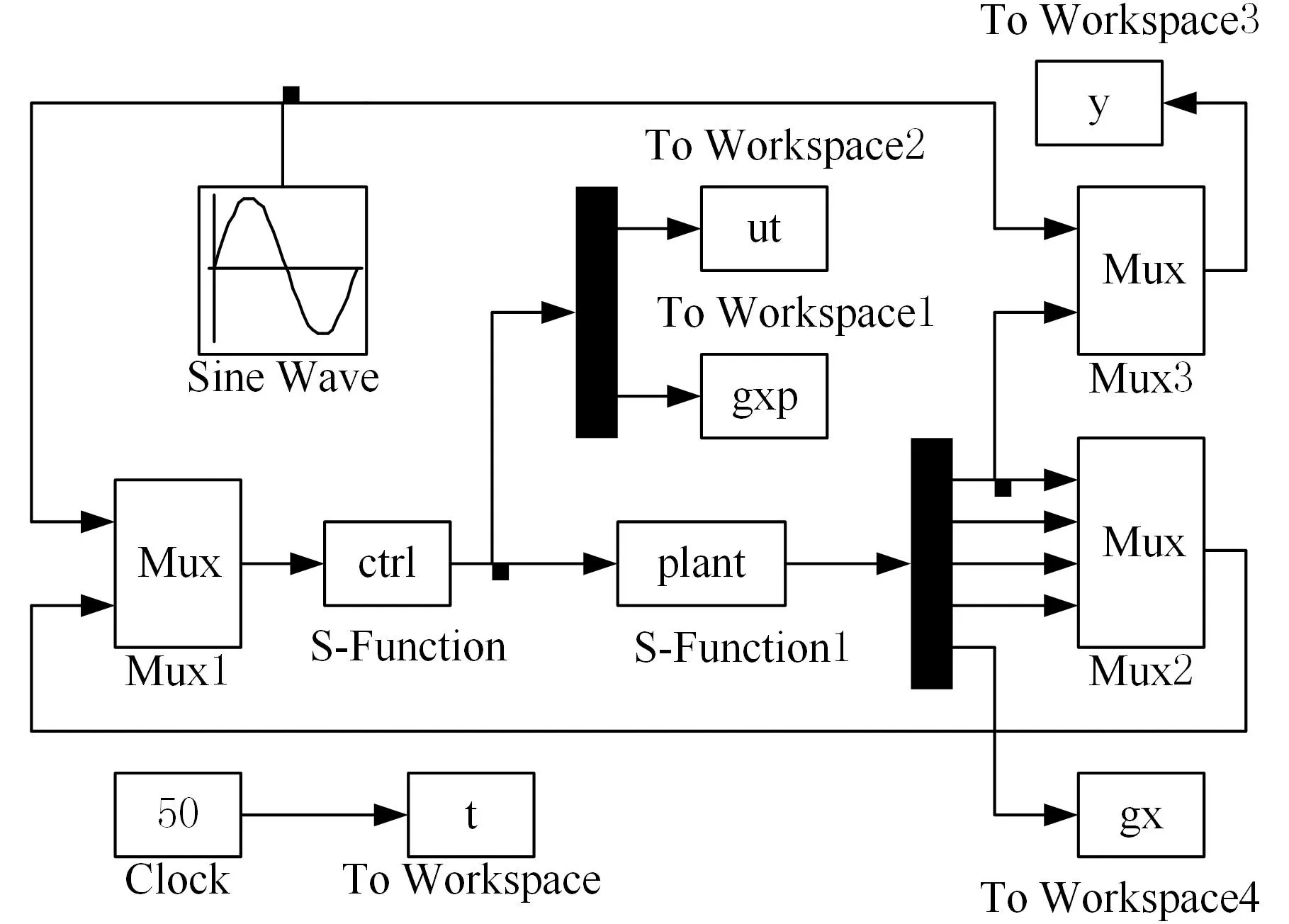
图3　单连杆柔性机械臂系统Simulink仿真框图

图4　位置跟踪

图5　控制输入

图6　g(x)及其估计值

仿真结果表明，采用神经网络反演法对机械臂进行控制，能保证对象跟踪误差在1 s后收敛于0。神经网络反演控制器的设计不但降低了基本的反演控制器对被控对象参数的敏感性，而且克服了传统方法对被控对象模型精确的要求。因此该方法对柔性机械臂的控制具有一定的有效性。

3　结语

本文首先建立六自由度柔性关节的简化模型，然后利用Lagrange法创建动力学模型。文中只考虑机械臂关节的柔性，忽略杆的柔性，将杆视为刚性杆。建模需要考虑各个电机和连杆的动能与势能，及每个关节的弹性势能，因此推导出整个关节机械臂的动力学方程。之后，以单自由度柔性机械臂为例，采用神经网络反演法对其控制器进行设计，得到具体的控制器模型以及控制律。最后给出具体的被控对象参数以及控制器参数，在Simulink中对其进行仿真，实例证明神经网络反演法对柔性机械臂的控制具有一定的可行性。

[1]唐国潮，金国光，刘远. 柔性机械臂动力学建模及特性研究[J]. 机械科学与技术，2009，28(8)：1031-1034.

TangGuochao，JinGuoguang，LiuYuan.DynamicModelingandPerformanceAnalysisofaFlexibleArm[J].MechanicalScienceandTechnologyforAerospaceEngineering, 2009，28(8)：1031-1034.

[2]谭民，王硕. 机器人技术研究进展[J].自动化学报，2013，39(7): 963-972.

TanMin，WangShuo.ResearchProgressonRobotics[J].ActaAutomaticaSinica，2013，39(7)：963-972.

[3]郭振锋，金国光，畅博彦，等. 刚-柔性机械臂动力学建模及其动力学特性研究[J]. 天津工业大学学报，2013，32(1)：70-74.

GuoZhenfeng，JinGuoguang，ChangBoyan，etal.ResearchofDynamicModelingandPerformanceforRigid-flexibleManipulators[J].JournalofTianjinPolytechnicUniversity，2013，32(1)：70-74.

[4]沈孝栋，刘长毅，张柏寿. 考虑关节柔性的机器人制孔过程动力学仿真[J]. 机械设计与制造，2015(3)：196-200.

ShenXiaodong，LiuChangyi，ZhangBoshou.DynamicSimulationofRoboticDrillingProcesswithJointFlexibilityConsidered[J].MachineryDesign&Manufacture，2015(3)：196-200.

[5]UlrichS，SasiadekJZ，BarkanaI.NonlinearAdaptiveOutputFeedbackControlofFlexible-jointSpaceManipulatorswithJointStiffnessUncertainties[J].JournalofGuidance，Control，andDynamics，2014,37(6):1961-1975.

[6]刘广瑞，吴晓铃，陈园，等. 末端质量和关节惯量对柔性臂运动稳定性的影响分析[J]. 中国机械工程，2014，25(4)：480-485.

LiuGuangrui，WuXiaoling，ChenYuan，etal.AnalysisofInfluencesofEndPositionMassandJointRotaryInertiaonMotionStabilityofaFlexibleManipulatorArm[J].ChinaMechanicalEngineering，2014，25(4)：480-485.

[7]刘旭亮，黄玉平，崔佩娟，等. 柔性机械臂建模及动力学特性分析[J]. 噪声与振动控制，2014,34(6):7-11.

LiuXuliang，HuangYuping，CuiPeijuan，etal.ModelingandDynamicCharacteristicAnalysisofFlexibleRoboticArm[J].NoiseandVibrationControl，2014，34(6)：7-11.

[8]胡小平,张文辉,季晓明. 漂浮基空间柔性机械臂基于神经网络的逆模控制[J]. 中国机械工程，2013，24(8)：1023-1027.

HuXiaoping，ZhangWenhui，JiXiaoming.SpaceFlexibleRoboticManipulatorsBasedonNeuralNetwork[J].ChinaMechanicalEngineering，2013，24(8)：1023-1027.

[9]JongHO，JinSL.ControlofFlexibleJointRobotSystembyBacksteppingDesignApproach[C]//Proceedingsofthe1997IEEE，InternationalConferenceonRoboticsandAutomation.Albuquerque,NewMexico，USA,1977:3435-3440

(编辑张洋)

Dynamics Analysis of 6-DOF Manipulators with Flexible Joints

Wang Hai1Fu Bangchen1,2Xue Bin1Yang Chunlai1

1.Anhui Polytechnic University，Wuhu，Anhui，241000 2.Anpu Institute of Technology Robotic Industry Co., Ltd., Wuhu，Anhui，241000

Most robots were hypothetical designed and controlled in rigid body dynamics. Hence, the accuracy and efficiency of these robots were limited in working. However, the flexible joint manipulators provided a good point of these problems. The 6-DOF manipulator with flexible joints was studied herein. Firstly, a simplified model was given, and the kinetic model of this manipulator was built by Lagrange equations. Then, the control law was created by neural network backstepping method in the case of 6-DOF manipulator with flexible joints. Finally, the rationality of the controller was proven by Simulink.

6-DOF； flexible joint； dynamics； Lagrange equation； neural network backstepping method

王海，男，1976年生。安徽工程大学机械与汽车工程学院教授、博士。主要研究方向为微纳米技术和机器人测控。发表论文20余篇。付邦晨，女，1992年生。安徽工程大学机械与汽车工程学院硕士研究生，芜湖安普机器人产业技术研究院有限公司工程师。薛斌，男，1990年生。安徽工程大学机械与汽车工程学院硕士研究生。杨春来，男，1982年生。安徽工程大学机械与汽车工程学院讲师、博士。

2015-06-08

国家自然科学基金资助项目(51175001，51275001，51375469)；安徽省自然科学研究计划资助项目(KJ2012A003)

TP241

10.3969/j.issn.1004-132X.2016.08.018