模具边界邻域气压砂轮进动光整轨迹优化

蔡东海　计时鸣　张鹤腾　金明生

浙江工业大学特种装备制造与先进加工技术教育部/浙江省重点实验室，杭州，310032



模具边界邻域气压砂轮进动光整轨迹优化

蔡东海计时鸣张鹤腾金明生

浙江工业大学特种装备制造与先进加工技术教育部/浙江省重点实验室，杭州，310032

针对气压砂轮进动光整在模具边界区域的振动加剧和边界棱线过度磨损等问题，提出在进动光整轨迹规划过程中对气压砂轮与工件相对切削速度方向进行约束的方案，推导出边界约束条件，并编写具有边界约束条件的进动光整轨迹生成程序。优化后的进动光整轨迹在连续曲面/平面内采用常规的进动光整方法，在边界附近采用具有约束的进动光整方法，因此兼具了进动光整方法切削速度方向的无序性优势，又避免了在工件边界附近引起剧烈振动和材料过度去除等问题。应用边界约束条件后的进动光整轨迹相比无约束的进动光整轨迹，在边界附近具有更小的振动和更完好的边界线，对加工过程和加工结果的改善在实际加工中得到了验证。

气压砂轮；轨迹规划；边界约束条件；振动

0　引言

为解决高硬度、高耐磨性自由曲面的高效精密光整加工难题文献[1-3]提出了一种基于软固结磨粒气压砂轮的光整加工新方法。该方法是对气囊抛光方法[4-9]的一种改进，将游离的磨粒固结在气囊橡胶基体表面，即成为气压砂轮。

影响气压砂轮光整效果的因素有许多，其中轨迹规划将直接影响光整质量和光整效率。气压砂轮采用进动轨迹进行光整能有效地提高被加工表面切削速度方向的无序性，提高表面光整质量。张彦等[10]通过研究发现在双面抛光运动过程中运动轨迹分布不但影响加工效率，而且影响工件表面质量；施春燕等[11]针对规则运动轨迹带来规则的误差分布和伪随机轨迹运动方式的缺点，提出了一种采用随机轨迹抛光的新方法；陈国达等[12]对气囊抛光方法以等残余面形误差为目标进行了轨迹规划,得出了驻留点间距的优选方案。

气压砂轮光整加工方法采用六自由度工业机器人控制气压砂轮。在实际加工过程中发现，在连续曲面上如果采用单纯的进动方式，气压砂轮自转轴可以绕着加工点法线做α为0～360°的整周转动，使气压砂轮在模具表面的切削速度无序化，但是，当接触面中心移动到与边界线的距离小于接触面半径时，即当气压砂轮移动到工件边缘区域时，原本圆形的接触面无法与工件保持完整接触，气压砂轮自转轴绕加工点法线转动过程中，会出现α取值在某一范围时，气压砂轮工具出现振动加剧、边界材料过度磨损和磨粒严重脱落现象。这表明，单纯采用进动方式光整不能满足边界附近高质量、高稳定性光整的要求。

本文对气压砂轮光整原理进行分析，确定了气压砂轮在工件边界附近合理的姿态角范围，并通过自编程软件生成了具有约束条件的进动轨迹抛光程序，极大程度地改善了上述现象。

1　气压砂轮进动光整原理及限制

气压砂轮进动光整原理如图1所示，自转速度ω1起光整作用，公转速度ω2起改变接触区切向速度方向的作用。

图1　气压砂轮进动光整原理

当接触中心O1运动到与模具边界线的距离小于接触面半径时，气压砂轮出现畸变，此时若气压砂轮自转轴处于图2所示的状态时，就会出现加工不稳定的现象。

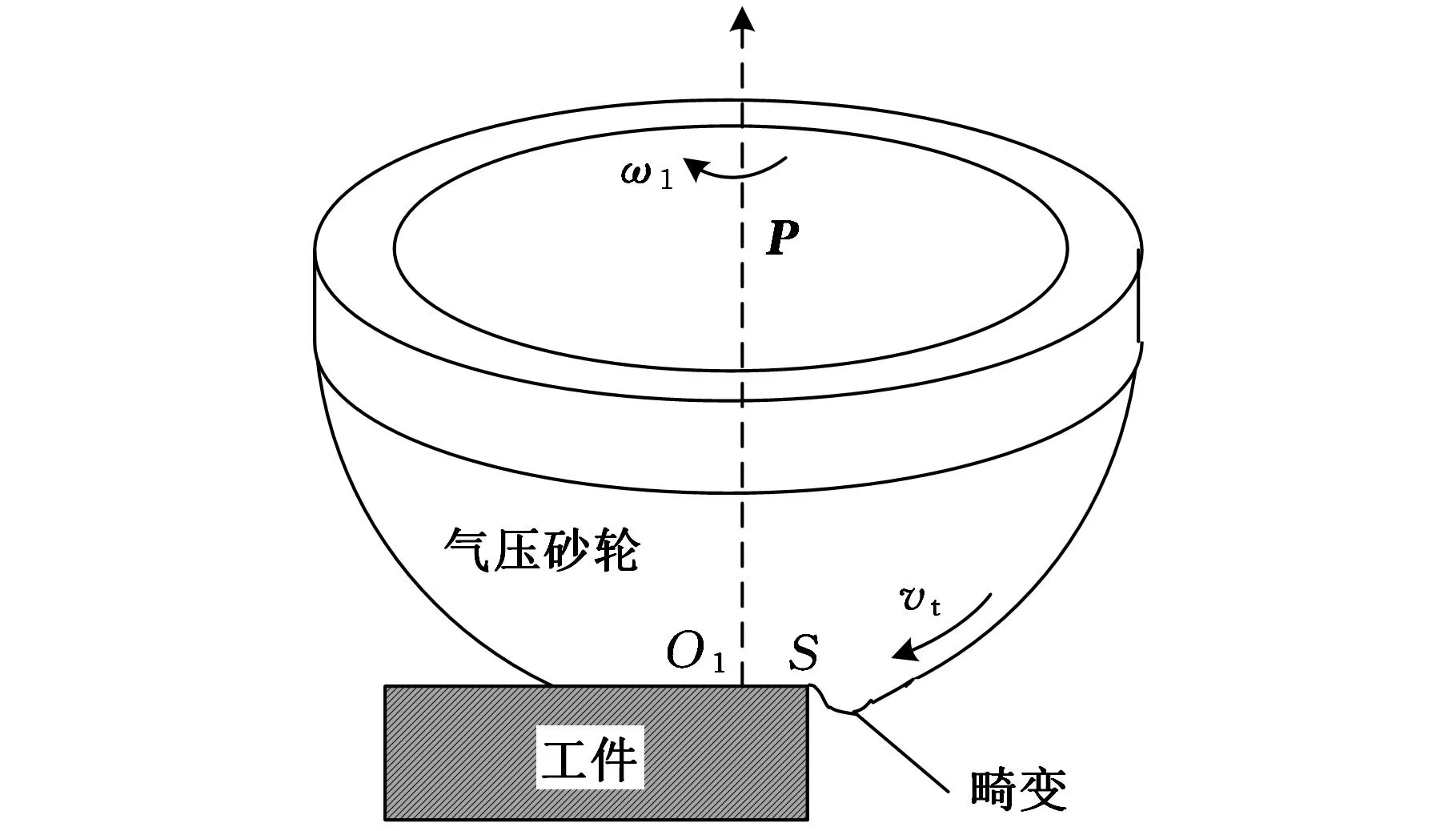
(a)气压砂轮的畸变

(b)畸变部位放大图2　边界附近气压砂轮畸变现象

图2中，矢量P由纸面内倾斜着指向纸面外，S点为工件边缘线上一点，在该状态下，气压砂轮在S点受力F1方向与S点气压砂轮外轮廓切线垂直，且在气压砂轮P轴旋转力矩的作用下，压紧S点，故F1远远大于其他正常接触区的受力F0，从而导致S点处的切削力大于其他位置，引起边界材料过度磨损；同时，S点处气压砂轮受到F1的反力作用，加工面内的分力大于正常切削力，导致气压砂轮朝边界外法向方向跳动，从而引起气压砂轮的振动加剧。

因此，对气压砂轮采用进动轨迹光整方法进行改进，避免上述现象出现，使其满足在边界附近的高质量光整要求就显得十分重要。

2　边界附近合理姿态角范围

气压砂轮与工件相对的切削速度方向分布为圆弧形[13]，为了推导和计算的方便性，首先假设：接触面上切削速度vt分布如图3所示，方向垂直于气压砂轮自转轴在接触面上的投影O1P1。

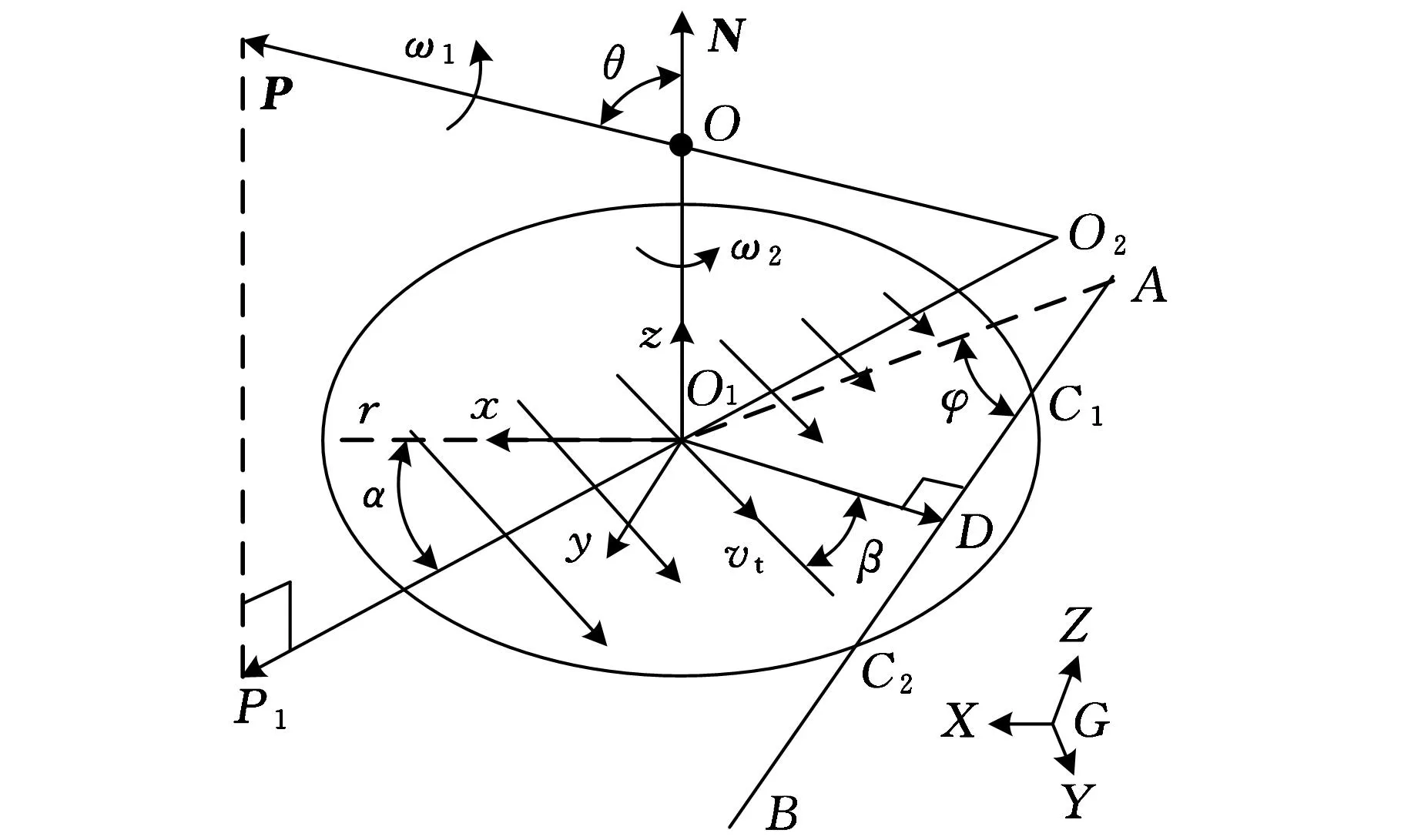
图3　接触面与边界线相交的情况

图3中，约束半径为r的圆形接触区与边界线AB相交，得到交点C1、C2；D是AB上一点，且O1D⊥AB，则O1D是边界AB的外法向；β是速度vt的方向与O1D的夹角；向量N是接触区的法向量；向量O2P为气压砂轮自转角速度ω1的方向向量，符合右手螺旋定则；在O1点建立局部直角坐标系O1xyz，它跟随加工工具一起运动；O2P1为O2P在接触区的投影向量。于是得到

(1)

式(1)表明切削速度vt的方向可由向量N和向量O2P进行叉乘得到，并将其定义为向量K，于是

(2)

从而得

(3)

经过对图2所示加工状态的分析可知，使光整过程平稳主要是气压砂轮在自转力矩作用下压紧边界线造成的，故只要改变边界线处气压砂轮自转力矩方向，即切削速度方向即可，因此得到β的极限范围：

0°≤β<90°

(4)

即切削速度vt不能存在沿着O1D反方向的分速度，气压砂轮自转力矩就不会影响边界处的受力状态。

由图3还可得出，D是C1和C2的中点，C1和C2是圆与线段的交点，可由方程求出，然后由下式判断交点是否在直线内：

(5)

线段外的交点是无效的交点。尽管在只有一个线段内交点的情况下夹角β的极限范围可能扩大，但变化幅度不会很大，因此，只有一个线段内交点的处理与两个线段内交点相同；当没有线段内交点时，夹角β范围不受该边界影响。

将式(1)和式(4)代入式(2)，得到边界约束条件：

N×O2P·O1D>0

(6)

其中，各点法向量N由三维建模软件UG导出的加工轨迹给出，可认为是已知的。

为了减小因假设带来的误差，在实际应用式(6)时可取一个正数ε作为临界值，即

N×O2P·O1D>ε

(7)

在已知点A、点B和点O1坐标的情况下，易得

O1D=AD-AO1

(8)

(9)

(10)

(11)

根据前期推导出的坐标系转换方法和进动角计算公式[11]，可以方便地将局部坐标系O1xyz中由倾角θ和进动角α表示的向量OP通过坐标变换转换成全局坐标系GXYZ下的旋转轴向量OP。若电机的转向如图3中ω1所示，则式(7)取O2P=OP，否则取O2P=-OP。

3　带约束进动轨迹的生成

根据上述方法利用自编程软件编写了具有边界约束条件的进动光整轨迹生成程序。

以100mm×60mm×20mm长方体工件上表面光整加工为例说明轨迹规划过程，以下是主要步骤：

(1)在UG中进行建模并生成原始的刀位数据。

(2)输入主要边界线坐标，如表1所示。

表1　边界数据　mm

(3)计算有约束的进动轨迹。首先设置与光整任务有关的各项参数，为了方便观察轨迹规划是否能够满足边界约束要求，设置了较大的进给速度和较小的进动角速度ω2，图4所示为轨迹规划参数设置界面。

图4　轨迹规划参数设置界面图

结合前两个步骤的数据，得到边界约束的进动光整轨迹，为了观察该轨迹是否符合要求，将O1点切削速度vt的方向作为考察对象，绘制结果如图5所示。主要计算流程如图6所示。

(a)有约束切削速度分布

(b)无约束切削速度分布图5　切削速度分布

图6　有约束进动轨迹计算流程

图5中，粗方框为长方体工件上表面边界线，折线表示加工路径，折线上的短线段表示切削速度方向。不难看出，与图5b无约束切削速度分布相比，图5a中切削速度方向在靠近边界的地方都是指向边界线的，亦即满足切削速度不存在沿着边界外法向反方向的分速度，也就是边界约束条件；而在远离边界的连续平面或曲面内，切削速度方向与X轴夹角范围可以取0～360°，即ω2不变，这与图5b无约束的切削速度分布无异。图5表明，生成有约束的进动轨迹满足边界约束条件，同时又有进动功能。

最后将计算得到的轨迹写入机器人可识别的JBI指令文件即可。

4　实验对比

为了验证式(7)给出的约束条件在实际光整中的作用，设计了对比实验。实验系统主要由六自由度工业机器人MOTOMAN-HP20(可实现位姿控制和轨迹控制)、气压砂轮抛光工具、信号调理和采集系统和工件组成，如图7所示。设计两个实验组，实验组1为无约束状态，实验组2为有约束状态，工件表面的原始粗糙度为Ra=0.8μm。实验中对两个矩形工件的同一边界附近分别进行无约束和有约束进动光整，其他参数相同。加工参数见表2，加工效果及振动情况分别见图8和图9，光整后无约束组工件表面粗糙度提升到Ra=0.32μm，有约束组工件表面则提升到Ra=0.15μm。

表2　加工参数

(a)实验设备

(b)实验过程图7　边界进动光整过程与传感器安装

(a)无约束光整效果

(b)无约束光整棱线部位放大

(c)有约束光整效果图8　加工效果对比

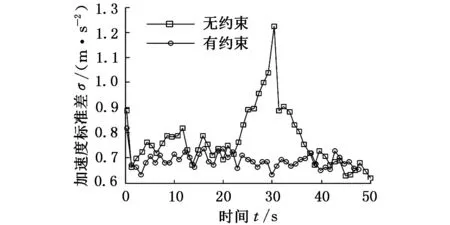
图9　加速度标准差对比

令气压砂轮头沿着边界线进行无约束的进动光整，并使用加速度传感器采集整个过程的振动信号。由于信号标准差能够很好地反映信号在时域中幅值的变化趋势[14]，因此实验数据处理时将振动信号分割成若干段，分别计算信号的标准差作为判定振动强烈程度的指标。

由图8所示的光泽度可看出，中间段棱线被磨损而出现凹陷，其材料去除程度明显大于表面正常加工区域；图8c所示的边界线的磨损不明显，但是由于前面的假设，认为切削速度都是同向均匀的，而实际切削速度方向是以O2为中心的同心圆，因而导致了在极限姿态角附近会出现轻微磨损。其解决方法是，增大约束条件式(7)右边的ε，以缩小边界附近加工姿态范围。

同时，从图9的振动信号标准差曲线可看出，20～40s内无约束进动光整的振动强度出现了一个尖峰，其值约为正常加工时振动强度的两倍，这种振动会改变材料去除模型，使得加工效果偏离预计；而采用有边界约束的进动光整方法后，整个过程的振动强度基本不变，维持在正常的振动状态下，因此，切削模型不会发生改变。这一结果表明了前述约束算法能明显提高进动光整方法的振动稳定性。

5　结论

(1)通过对气压砂轮进动原理进行研究分析，得出了模具边界邻域内使用进动光整方法的限制。

(2)气压砂轮在模具边界邻域内切削速度方向存在沿着边界外法向相反方向的分量是引起加工不稳定的主要原因。据此推导得出了气压砂轮进动光整的边界约束条件表达式。

(3)编写了具有边界约束条件的气压砂轮进动光整轨迹规划程序，该程序的可行性在实验中得到了充分证实。

(4)通过实验对比，验证了边界约束条件可以减弱气压砂轮在模具边界邻域内使用进动光整方法引起的振动不稳定并解决边界棱线过度磨损的问题。

[1]计时鸣, 许亚敏, 金明生, 等. 软固结磨粒气压砂轮的力学分析[J]. 中国机械工程, 2012,23(19):2366-2372.

JiShiming,XuYamin,JinMingsheng,etal.MechanicalAnalysisofPressureGrindingWheelwithSoftAbrasiveConsolidation[J].ChinaMechanicalEngineering, 2012,23(19):2366-2372.

[2]许亚敏. 软固结磨粒气压砂轮的光整加工技术及实验研究[D]. 杭州: 浙江工业大学, 2011.

[3]张鹤腾. 气压砂轮光整加工振动稳定性研究[D].杭州: 浙江工业大学,2013.

[4]WalkerDD,BrooksD,KingA,etal.The“Precessions”ToolingforPolishingandFiguringFlat,SphericalandAsphericSurfaces[J].OpticsExpress, 2003, 11(8): 958-964.

[5]WalkerDD,BrooksD,FreemanR,etal.NewDevelopmentsinthePrecessionsProcessforManufacturingFreeform,Large-optical,andPrecisionMechanicalSurfaces[J].SPIE, 2005, 6148: 51-60.

[6]高波, 谢大纲, 姚英学, 等. 气囊式工具抛光新技术[J]. 光学技术, 2004, 30(3): 333-335.

GaoBo,XieDagang,YaoYingxue,etal.NewTechnologyofBallonetToolforPolishing[J].OpticalTechnique, 2004, 30(3): 333-335.

[7]宋剑锋,姚英学,谢大纲, 等. 超精密气囊工具抛光方法的研究[J]. 华中科技大学学报(自然科学版), 2007, 35(S1): 104-107.

SongJianfeng,YaoYingxue,XieDagang,etal.StudyonUltra-precisionBonnetToolPolishingMethod[J].JournalofHuazhongUniversityofScienceandTechnology(NatureScience),2007, 35(S1): 104-107.

[8]计时鸣, 金明生, 张宪, 等. 应用于模具自由曲面的新型气囊抛光技术[J]. 机械工程学报, 2007, 43(8): 2-6.

JiShiming,JinMingsheng,ZhangXian,etal.NovelGasbagPolishingTechniqueforFree-formMold[J].ChineseJournalofMechanicalEngineering, 2007, 43(8): 2-6.

[9]金明生, 计时鸣, 张利, 等. 连续进动气囊抛光行间距优化及实验研究[J]. 中国机械工程, 2013,24(7):861-865.

JinMingsheng,JiShiming,ZhangLi,etal.LineSpacingOptimizationandExperimentalResearchofGasbagPolishingwithContinuousPrecession[J].ChinaMechanicalEngineering, 2013,24(7):861-865.

[10]张彦, 李军, 朱永伟,等. 双面抛光运动的数学建模及轨迹优化[J]. 光学技术, 2011, 37(3):279-283.

ZhangYan,LiJun,ZhuYongwei,etal.MathematicalModelingandTrajectoryOptimizationofDouble-sidedPolishingProcess[J].OpticalTechnique, 2011, 37(3):279-283.

[11]施春燕, 袁家虎, 伍凡,等. 运动轨迹对抛光误差的影响分析和轨迹优化研究[J]. 光学学报, 2011, 31(8):252-256.

ShiChunyan,YuanJiahu,WuFan,etal.AnalysisofPolishingErrorsbyToolPathsandOptimizationofToolPaths[J].ActaOpticaSinica, 2011, 31(8):252-256.

[12]陈国达,计时鸣,金明生,等. 面向等残余面形误差的分层修形模具气囊抛光轨迹规划方法[J]. 兵工学报, 2012, 33(6): 724-729.

ChenGuoda,JiShiming,JinMingsheng,etal.LayeringShapingMouldGasbagPolishingTrajectoryPlanningMethodforEqualResidualFigureError[J].ActaArmamentarii, 2012, 33(6): 724-729.

[13]金明生. 模具自由曲面气囊抛光机理及工艺研究[D]. 杭州：浙江工业大学,2009.

[14]罗作国. 切削颤振辨识及主动抑制策略的研究[D]. 武汉：华中科技大学,2007.

(编辑郭伟)

Pneumatic Wheel Precession Finishing Trajectory Optimization in Neighborhood of Mould Boundaries

Cai DonghaiJi ShimingZhang HetengJin Mingsheng

Key Laboratory of E&M, Ministry of Education & Zhejiang Province,Zhejiang University of Technology,Hangzhou,310032

For the vibration intensified and excessive removal of material in finishing the neighborhood of mould boundaries by pneumatic wheel precession finishing technology, the direction constraint of relative cutting speed was applied in precession finishing trajectory planning process and the boundary constraint conditions were derived. Then the precession finishing trajectory generation program with boundary constraint conditions was compiled. The optimized precession finishing trajectory means used the normal precession to finish the continuous surface and used constraint precession to finish the boundary. It provided with disordered cutting directions and avoided vibration intensified and excessive removal of material. Precession finishing trajectory with boundary constraint conditions had even smaller vibration and more intact boundary line, compared to unconstrained precession finishing trajectory. This boundary constraint conditions improve both of the process and the outcome of pneumatic wheel precession finishing method, and has been verified at the actual processing.

pneumatic wheel; trajectory planning; boundary constraint condition; vibration

蔡东海，男，1982年生。浙江工业大学机械工程学院助理研究员。主要研究方向为超精密加工。计时鸣，男，1957年生。浙江工业大学机械工程学院教授、博士研究生导师。张鹤腾，男，1987年生。浙江工业大学机械工程学院硕士研究生。金明生，男，1982年生。浙江工业大学机械工程学院副教授。

2015-06-09

国家自然科学基金资助项目(51175471，51205358)；浙江省科技厅创新团队资助项目(2011R50011-07)；浙江省科技厅公益性技术应用研究计划资助项目(2015C31060)

TH16;TP391;TG5806

10.3969/j.issn.1004-132X.2016.08.016