路基边坡降雨试验及基于神经网络的水分场研究

吴谦，王常明，王天佐，黄晓虎，张志敏，张兆楠

（吉林大学 建设工程学院，吉林 长春，130026）

路基边坡降雨试验及基于神经网络的水分场研究

吴谦，王常明，王天佐，黄晓虎，张志敏，张兆楠

（吉林大学 建设工程学院，吉林 长春，130026）

为了研究降雨条件下路基边坡土体含水率的变化规律及雨水入渗过程，进行一系列不同降雨强度、不同坡度条件下的室内降雨模拟试验。以土体含水率受降雨历时、土体空间位置、坡度和降雨强度这4个因素作为输入单元，体积含水率作为输出单元，选取试验数据输入训练，建立含水率的遗传算法神经网络预测模型。预测检验后，利用神经网络对2.7 mm/min降雨强度下40°边坡的降雨入渗过程进行预测研究。研究结果表明：对于路基边坡，当土的性质、压实度、排水等条件相同时，土体含水率受降雨历时、土体空间位置、坡度和降雨强度这4个因素共同影响；随降雨的进行，土体含水率逐渐增加，浸润范围不断增大，受空间位置影响距入渗面越远则含水率变化滞后，增长速率及幅度减小；在相同雨强下，不同坡度边坡坡顶土体含水率变化过程相似，而随坡度的增大，坡脚土体含水率的增长速率及幅度逐渐减小；随雨强的增加同一边坡相同位置处土体含水率越早开始增大，其增长速率及幅度也随之增加；利用所建立的含水率遗传算法神经网络预测模型所得入渗结果与试验观测结果接近，表明该神经网络方法能较好地描述路基边坡土体含水率的变化情况及雨水的入渗过程。

路基边坡；土体体积含水率；遗传算法神经网络；预测模型；入渗过程

土体含水率对其工程特性具有重要影响。在降雨过程中，随着非饱和土体含水率的增加，其各种指标随之变化［1］。许多学者对降雨过程中土体含水率的变化规律进行了研究，目前研究方法主要集中在2个方面：一是通过埋设含水率探头测得土体含水率，包括现场原位试验［2-4］和物理模拟试验［5-7］方法；二是通过基于饱和非饱和渗流的数值计算方法［8-9］。采用这些试验方法可以得到各监测点含水率的变化过程、土体中含水率的分布特征、湿润锋运移过程等信息，但通常受限于测量空间范围、测量时间等因素，只有借助数值计算方法或合理的预测方法才可将试验在空间、时间或其他因素上进行延伸，目前采用较多的是数值方法。当采用数值方法时，边坡土体物理参数不易准确获取，土体参数在坡体内分布是否均匀会对计算结果造成很大影响，而边坡土体含水率的预测方法至今仍不清楚。边坡土体含水率变化是一个复杂的非线性问题，对于路基一类的均质土坡来说，土的工程性质、压实度、排水条件等相同，其土体含水率由降雨强度、降雨历时、土体空间位置、坡度4个因素共同控制，普通数学模型很难对土体含水率变化过程进行准确描述，在研究中若只考虑某个单一指标与含水率之间的联系，而不是同时考虑这些因素共同作用下土体含水率的变化情况，那么分析结果必然存在片面性。如何解决各影响因素相互组合时相互之间的非线性联系是其中的难点。神经网络方法具有并行分布与存储、自组织、自学习的功能，能分析较复杂的非线性系统，其在工程上的应用［10-11］给我们提供了解决问题的新思路。基于此，本文作者进行路基边坡的室内降雨模拟试验，试验中土的性质、压实度、排水等条件相同。试验主要研究以下3个方面：1） 不同降雨强度下边坡含水率的变化规律；2） 不同坡度边坡含水率变化规律；3） 同一边坡内不同位置含水率的变化规律。根据试验结果建立含水率的遗传算法神经网络预测模型，实现对土体含水率随降雨历时变化的预测，同时实现湿润锋在坡体内运移过程的预测，旨在为边坡土体含水率的研究提供新的思路和方法。

1　边坡降雨模拟试验

1.1试验内容

本次实验研究1.5 mm/min和2.1 mm/min降雨强度下40°～70°边坡和2.7 mm/min降雨强度下30°～70°边坡不同位置土体体积含水率的变化情况。试验中，降雨持续时间为60 min，试验设计见表1。

1.2试验装置与测量系统

试验装置由人工降雨设备、试验槽、沉砂池相结合，在试验过程中，边坡土体的体积含水率由MPU-8型高精度微型土壤墒情自动采集器测得。图1所示为试验装置示意图（以边坡40°为例）。

1.3边坡模型

表1　试验设计安排Table 1 Test plan

图1　试验装置Fig. 1　Test device

试验采用辽西黄土，根据粒度成分测试结果，辽西黄土以粉粒为主，粉粒质量分数为53.86%～82.24%，平均为72.87%；黏粒质量分数为11.67%～33.26%，变化较大，平均为18.87%。黄土基本物理力学参数见表2，其实测水土特征曲线及根据VAN GENUCHTEN［12］， FREDLUND and XING［13］和GARDNER［14］这3种经典水土特征曲线模型所得的拟合曲线见图 2。经先期试验测试，当边坡土体初始含水率为10%时，模拟效果最佳。试验前，将土料晒干后，计算所需加水量，配制试验用土。采用分层填筑法筑坡，每层厚度10 cm，分4层，利用触探仪控制每层土压实度一致，边坡模型的压实度为 85%，最后针对不同角度进行人工削坡。

表2　黄土的物理力学参数Table 2 Physical and mechanics parameters of soil

图2　水土特征曲线Fig. 2　Soil-water characteristic curves

1.4降雨模型试验结果

1.4.1含水率随降雨时间的变化规律

雨水的入渗过程如图3所示。从图3可见：随着降雨的进行，土体的浸润深度不断增大，同时在达到饱和含水率之前，雨水的不断入渗也使土体的含水率持续增加。

1.4.2不同空间位置含水率变化规律

2.7 mm/min降雨强度下40°边坡坡面浅埋（距坡面3 cm，距坡顶10 cm）探头测得土体体积含水率随时间变化曲线如图4所示。从图4可见：在5 min时，其含水率开始增加，含水率增长速率也不断增大；当降雨持续14 min时，含水率增长速率达到峰值，之后开始逐渐减小，含水率曲线也逐渐变得平缓；在试验进行至24 min时，含水率达到最大值后基本保持不变。而在坡体内部较深处（距坡面15 cm，距坡顶30 cm）土体含水率的增速较小，含水率增长缓慢，如图5所示。对比图4和图5可以发现：距离入渗面越近，含水率变化的速率和幅度越大；而距离入渗面越远，体积含水率的变化速率及幅度越小。这体现了入渗路径对土体含水率的控制作用。

图3　入渗过程示意图Fig. 3　Infiltration process

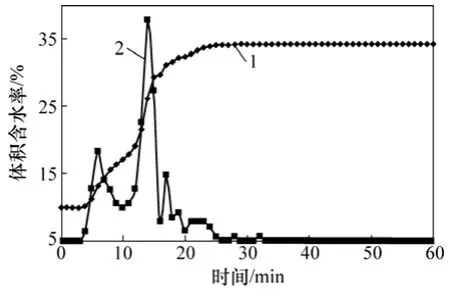
图4　浅部土体含水率变化曲线Fig. 4　Change curves of moisture content in shallow soil mass

1.4.3不同坡度含水率变化规律

2.7 mm/min降雨强度下，不同坡度边坡坡顶土体（距坡面约3 cm，距坡顶约10 cm）体积含水率的变化曲线如图6所示。从图6可见：随着降雨持续，坡顶土体含水率快速增大，当达到饱和状态后含水率基本保持不变；虽然坡度不同，但各边坡坡顶土体含水率变化规律相似。在2.7 mm/min降雨强度下，不同坡度边坡坡脚（距坡面约10 cm，距坡顶约30 cm）土体含水率变化如图7所示。从图7可见：随着降雨的进行，不同坡度边坡坡脚土体含水率变化有较大差异，坡脚土体含水率增长速率及其增长幅度随坡度增加逐渐变小；30°边坡坡脚土体含水率增长较快，在35 min时达到饱和并保持稳定；而 40°～70°边坡坡脚处土体含水率在 60 min时依次为 31.1%，26.3%，20.5%和19.5%。这主要是因为在重力作用下，边坡表面入渗的雨水有向坡脚汇集的趋势，坡度越小，则承接降雨的坡面越长，上部土体就会承接更多的雨水入渗，故在重力作用下会有更多雨水向坡脚汇集，从而导致此现象。

图5　深部土体含水率变化曲线Fig. 5　Change curves of moisture content in deep soil mass

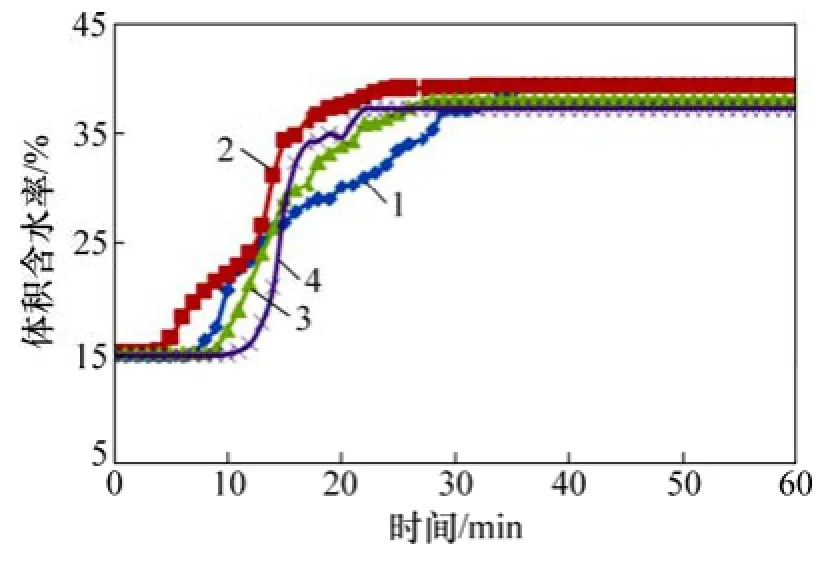
图6　不同坡度边坡坡顶土体含水率变化曲线Fig. 6　Change curves of moisture content in top of slopes with different slope angles

图7　不同坡度边坡坡脚土体含水率变化曲线Fig. 7　Change curves of moisture content in toe of slopes with different slope angles

1.4.4不同降雨强度下含水率变化规律

降雨强度直接影响边坡土体的含水率。以 40°边坡为例，不同降雨强度下坡脚（距坡面约10 cm，距坡顶约30 cm）位置含水率变化过程如图8所示。从图8可见降雨强度对土体含水率的影响主要变现在：1） 相同位置监测点处土体含水率及其增长速率随降雨强度的增加而增加；2） 降雨强度的增加加快了坡体内浸润峰的运移速率，降雨强度越大，则相同位置处土体的含水率越早开始增大。

图8　不同降雨强度下含水率变化曲线Fig. 8　Change curves of moisture content with different rainfall intensities

2　含水率的遗传算法神经网络预测

2.1基本原理

BP神经网络在工程界被广泛使用，虽然其具有较强的局部寻优能力，但由于其训练过程中是基于梯度算法来调整权值和阈值，在优化过程中存在陷入局部最小值的可能，同时梯度算法网络收敛速度慢，也导致训练时间变长。遗传算法作为一种全局寻优的算法，且具有较快的收敛速度，借助遗传算法的这些优点，所建立的网络将会有更快的收敛速度且能克服BP神经网络容易陷入局部最优等缺点［15］。遗传算法优化BP神经网络是使用遗传算法优化网络的权值和阈值，使优化后的网络能够更好地预测函数输出。

2.2输入输出单元的确定

选取降雨历时、土体空间位置（由距坡面水平距离H与距坡顶垂直距离V表征）、坡度和降雨强度作为输入单元，网络输入层节点数 n=5，输出量为土体体积含水率，输出层节点数m=1。

2.3网络的训练

选取 1.5 mm/min降雨强度下 40°～70°边坡、2.1 mm/min降雨强度下40°～70°边坡和2.7 mm/min降雨强度下30°～60°边坡中不同位置共73个监测点的试验监测数据对网络进行训练。网络隐含层节点数l由下式确定：

式中：a为0～10之间的常数，通过试算最终确定网络结构为5-14-1。其中隐含层的传递函数为tansig函数，输出层传递函数为 purelin函数，网络训练函数采用trainlm函数，网络中指定学习速率为 0.001，网络误差为0.000 1。遗传算法在寻优过程中的个体适应度为BP网络的含水率预测输出与期望输出之间误差的绝对值之和；种群规模为50，进化次数为100，交叉概率Pc取0.9，变异概率Pm取0.05。未经优化BP网络需要331次迭代达才能到小于设定误差的目标，而遗传算法优化后只需要15次迭代即可达到设定误差。

2.4含水率的预测

网络训练完成之后用2.7 mm/min降雨强度下70°边坡土体体积含水率的试验监测数据作为预测检验样本，边坡中含水率探头位置见表 3。网络预测结果如图 9（a）所示。可以看出预测结果与期望输出（图 9（b））基本吻合。

表3　70°边坡内体积含水率探头埋设位置Table 3 Position of moisture sensors in slope with slope angle of 70° cm

图9　70°边坡土体体积含水率的预测输出与期望输出Fig. 9　Forecast output by neural network and desired output of slope with slope angle of 70°

分别采用 BP神经网络和遗传算法神经网络（GA-BP）预测得到的2.7 mm/min降雨强度下70°边坡中5个含水率探头处土体各时间点体积含水率与实测值之间的误差如图10所示。从图10可以直观地看出遗传算法神经网络预测输出与实测值之间的误差明显要比BP神经网络的低。结合图10（b），以坡顶处2号探头为例，BP神经网络预测结果最大相对误差为44%，最小相对误差为 0.24%；遗传算法神经网络预测最大相对误差为34%，最小相对误差仅为0.06%。从全局出发将网络预测输出值与实测值相比较，BP神经网络预测输出的平均相对误差为7.2%，遗传算法神经网络预测输出平均相对误差为3.7%。

网络预测输出的均方误差EMS用下式进行计算：

其中：ti为验证样本的期望输出；ai为网络的预测输出。BP神经网络的预测输出与实测值之间的均方误差为0.000 198，而遗传算法神经网络的预测输出与实际监测值之间的均方误差为0.000 109，说明遗传算法神经网络预测精度比BP神经网络的预测精度高，能较准确地描述降雨过程中路基边坡土体含水率的变化过程。

图10　网络预测误差Fig. 10 Forecast output errors of neural network

3　降雨入渗过程预测研究

利用神经网络，对2.7 mm/min降雨强度下40°边坡中雨水的入渗过程进行预测研究。网络的训练数据选取室内降雨试验中 3种降雨强度下所有边坡共 78个监测点的监测数据，网络结构、参数等与前面的相同。以5 cm间距在坡体内均匀选取77个含水率预测点，然后对这些预测点位置上土体的体积含水率随时间的变化进行预测。将得到的含水率进行插值得到含水率等值线图，见图11，图中黑色虚线表示湿润锋的位置。从图11可以看出：雨水的入渗是从坡面向坡体内部逐渐发展的，随着降雨的进行，雨水浸润范围不断增大，在初期含水率等值线受入渗路径控制基本平行于坡面；随着降雨的进行，坡脚的浸润范围比其他部位的大，而且这种趋势随着降雨的进行越来越明显。这是因为在降雨过程中，随着入渗到边坡内的雨量越来越多，重力在入渗过程中的作用逐渐凸显，除接受雨水直接入渗之外，上部土体中雨水在重力作用下不断向坡脚处汇集。

图11　40°边坡中含水率等值线图Fig. 11 Contour maps of moisture content in slope with angle of 40°

图 12所示为试验过程中利用相机透过有机玻璃记录的各时间点坡体内湿润锋的位置，与图11中依据预测数据得到的湿润锋位置较接近。

根据预测结果给出边坡中竖直方向x=10 cm和水平方向y=10 cm这2个水分剖面上含水率的分布及湿润锋的变化过程，见图13。从图13可见：降雨期间，由浅到深土体的含水率逐渐增加，在10 min时湿润锋已全部进入土体内，坡面开始积水入渗；此后，随降雨的进行，湿润锋不断向坡体内部移动，在重力作用下雨水不断向坡脚汇集，导致下部y=10 cm剖面上的入渗速率要大于x=10 cm剖面的入渗速率。图14所示为入渗过程中2个水分剖面上湿润锋位置的预测值与实测值对比。可以看出：图中数据点基本都落在 y=x直线上，表明预测值与实测值接近。线性回归数据统计结果见表4，表中回归方程的斜率均接近1.0，且线性回归的相关系数均较高。

图12　40°边坡中湿润锋的运移过程Fig. 12 Transport process of wetting fronts in slope with angle of 40° during test

图13　湿润锋运移过程Fig. 13 Transport processes of wetting front on section with x=10 cm and y=10 cm

表4　湿润锋位置预测值与实测值线性回归分析结果Table 4 Results of linear regression analysis of forecasted and measured wetting front position

图14　湿润锋位置预测值与实测值对比Fig. 14 Comparison between forecasted and measured wetting front position

4　结论

1） 室内模拟试验能够准确地测量降雨过程中边坡内部不同位置土体含水率的变化情况。对于路基边坡，土的性质、压实度、排水等条件相同，土体含水率由降雨历时、土体空间位置、坡度和降雨强度共同控制。随降雨的进行，土体含水率逐渐增大，浸润范围不断增大；受空间位置影响，距入渗面越远，则含水率变化滞后，增长速率及幅度减小；在相同雨强下，不同坡度边坡坡顶土体含水率变化过程相似，而随坡度的增大，坡脚土体含水率的增长速率及幅度逐渐减小；随雨强增大，同一边坡相同位置处土体含水率越早开始增大，其增长速率及幅度也随之增加。

2） 遗传算法优化后的BP神经网络具备更快的收敛速率，其预测输出与试验监测值接近，预测结果平均相对误差仅为3.7%，其均方误差仅为0.000 109，比传统BP神经网络的预测精度高。

3） 基于神经网络的含水率预测模型得到的湿润锋运移过程与试验观测结果基本吻合，且其很好地体现出重力作用下雨水向坡脚汇集这一实际现象。

4） 含水率的变化导致边坡各种指标变化。在进一步研究中，可将含水率的预测值与水土特征曲线联系起来计算边坡内吸力场的分布，得到土体抗剪强度，进而实现对边坡稳定性的评价。

［1］ FREDLUND D G， RAHADJO H. Soil mechanics for unsaturated soils［M］. New York： John Wiley and Sons Inc， 1993：1-21.

［2］ O’KANE M， WILSON G W， BARBOUR S L. Instrumentation and monitoring of an engineered soil cover system for mine waste rock［J］. Can Geotech J， 1998， 35（5）： 828-846.

［3］ TU X B， KWONG A K L， DAI F C， et al. Field monitoring of rainfall infiltration in a loess slope and analysis of failure mechanism of rainfall-induced landslides［J］. Engineering Geology， 2009， 105（1）： 134-150.

［4］ 李萍， 李同录， 王阿丹， 等. 黄土中水分迁移规律现场试验研究［J］. 岩土力学， 2013， 34（5）： 1331-1339. LI Ping， LI Tonglu， WANG Adan， et al. In-situ test research on regularities of water migration in loess［J］. Rock and Soil Mechanics， 2013， 34（5）： 1331-1339.

［5］ HUANG C C， YUIN S C. Experimental investigation of rainfall criteria for shallow slope failures［J］. Geomorphology， 2010，120（3）： 326-338.

［6］ 李焕强， 孙红月， 孙新民， 等. 降雨入渗对边坡性状影响的模型实验研究［J］. 岩土工程学报， 2009， 31（4）： 589-594. LI Huanqiang， SUN Hongyue， SUN Xinmin， et al. Influence of

rainfall infiltration on slopes by physical model test［J］. Chinese Journal of Geotechnical Engineering， 2009， 31（4）： 589-594.

［7］ 朱元骏， 邵明安. 含砾石土壤降雨入渗过程模拟［J］. 水利科学进展， 2010， 21（6）： 779-787. ZHU Yuanjun， SHAO Mingan. Simulation of rainfall infiltration in stony soil［J］. Advances in Water Science， 2010， 21（6）：779-787.

［8］ 蒋中明， 曾铃， 付宏渊， 等. 降雨条件下厚覆盖层边坡的渗流特性［J］. 中南大学学报（自然科学版）， 2012， 43（7）： 2782-2788. JIANG Zhongming， ZENG Ling， FU Hongyuan， et al. Seepage characteristics of thick coating slope in raining condition［J］. Journal of Central South University （Science and Technology），2012， 43（7）： 2782-2788.

［9］ 王铁行. 非饱和黄土路基水分场的数值分析［J］. 岩土工程学报， 2008， 30（1）： 41-45. WANG Tiehang. Moisture migration in unsaturated loess subgrade［J］. Chinese Journal of Geotechnical Engineering， 2008，30（1）： 41-45.

［10］ 徐黎明， 王清， 陈剑平， 等. 基于 BP神经网络的泥石流平均流速预测［J］. 吉林大学学报（地球科学版）， 2013， 43（1）：186-191. XU Liming， WANG Qing， CHEN Jianping， et al. Forecast for average velocity of debris flow based on BP neural network［J］. Journal of Jilin University （Earth Science Edition）， 2013， 43（1）：186-191.

［11］ 梁冰， 李刚， 王宗林. 基于BP 神经网络的降雨充水矿井涌水量预测［J］. 中国地质灾害与防治学报， 2009， 20（1）： 122-125. LIANG Bing， LI Gang， WANG Zonglin. Prediction of water inflow of mine with rainfall yield based on BP artificial neural network［J］. The Chinese Journal of Geological Hazard and Control， 2009， 20（1）： 122-125.

［12］ VAN GENUCHTEN M T H. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils［J］. Soil Science Society of America Journal， 1980， 44： 892-898.

［13］ FREDLUND D G， XING A Q. Equations for the soil-water characteristic crave［J］. Canadian Geotechnical Journal， 1994，31（4）： 521-532.

［14］ GARDNER W R. Field measurement of soil water diffusivity［J］. Soil Science Society of America Proceedings， 1970， 34（5）：832-833.

［15］ 潘昊， 王晓勇， 陈琼， 等. 基于遗传算法的BP计算机应用［J］.计算机应用， 2005， 25（12）： 2777-2779. PAN Hao， WANG Xiaoyong， CHEN Qiong， et al. Application of BP neural network based on genetic algorithm［J］. Computer Applications， 2005， 25（12）： 2777-2779.

（编辑 陈灿华）

Rainfall infiltration test on subgrade slope and study on moisture migration by neural network

WU Qian， WANG Changming， WANG Tianzuo， HUANG Xiaohu， ZHANG Zhimin， ZHANG Zhaonan

（College of Construction Engineering， Jilin University， Changchun 130026， China）

A series of rainfall tests with different rainfall intensities and different slope angles were carried out in laboratory to study the variation law of moisture content and the infiltration process in subgrade slope. According to the test results， the subgrade slope with the same engineering properties of soil， compaction degree and drainage condition were found， the moisture content was jointly influenced by four factors， i.e. rainfall duration， position of soil mass， slope angle and rainfall intensity. Taking the four factors as input units and the volume moisture content as output unit， the moisture content forecast model with genetic algorithm based on neural network was established. After prediction test，the neural network was used to forecast the infiltration process in slope with angle of 40° at rainfall intensity of 2.7 mm/min. The results show that as the rainfall lasts， the soil moisture content increases and the infiltrated area in the slope is extended. With the increase of distance from soil mass to infiltrate surface， the change of moisture content lags， and the increasing rate and amplitude of moisture content decrease. At the same rainfall intensity， the change process of moisture content at the top of the slopes with different slope angles is similar， whereas the increasing rate and amplitude of that at the toe of the slopes decrease with the increase of slope angle. When the slope angle remains unchanged， the increasing rate and amplitude of soil moisture content at similar position increase with the increase of rainfall intensity， and beginsto change earlier. The forecasted infiltration process in slope is consistent with the observation result by rainfall test，which indicates that the neural network can exactly forecast the variation of moisture content and infiltration process in subgrade slope.

subgrade slope； volume moisture content； genetic algorithm based neural network； forecast model；infiltration process

TU444

A

1672-7207（2016）04-1237-08

10.11817/j.issn.1672-7207.2016.04.021

2015-04-02；

2015-05-26

国家自然科学基金资助项目（40972171）；吉林大学研究生创新基金资助项目（2014065）（Project （40972171） supported by the National Natural Science Foundation of China； Project （2014065） supported by the Graduate Innovation Fund of Jilin University）

王常明，博士，教授，从事岩土力学研究；E-mail：wangcm@jlu.edu.cn