基于改进的M指标的库布齐沙漠沙丘潜在活性评价
2016-08-15哈斯额尔敦陶彬彬周炎广
管 超,哈斯额尔敦,陶彬彬,刘 丹,周炎广
基于改进的M指标的库布齐沙漠沙丘潜在活性评价
管超,哈斯额尔敦,陶彬彬,刘丹,周炎广
(北京师范大学资源学院,北京100875)
定量评估沙丘的潜在活性程度是沙漠及沙地动态研究的基础工作。目前对于沙丘潜在活性的研究主要是通过Lancaster给出的M指标(M=W/(P/ET)),然而针对我国地形复杂、气候多变,尤其西北干旱地区,此方法与实际情况有较大出入。本文以库布齐沙漠为例采用SEBS模型代替Thornthwaite方法计算蒸散量,并将年蒸散分为4部分代表4个季节计算,以提高蒸散量的精度,并结合地表粗糙度、NDVI、降水、风速等数据利用模糊模型提取各季沙丘潜在活性指数的区域分异,最后结合地貌分类图给出潜在活性的新分级标准。经验证明基于模糊模型的沙丘潜在活性评价可以综合多种影响因素,符合我国气候、地形条件下的真实状况,提高评价精度,同时也指出Lancaster的M指标并不适合我国的自然条件。
沙丘潜在活性;SEBS模型;模糊模型
管超,哈斯额尔敦,陶彬彬,等.基于改进的M指标的库布齐沙漠沙丘潜在活性评价[J].沙漠与绿洲气象,2016,10(3):21-29.
“沙丘潜在活性”是沙丘潜在动态变化的能力,是沙丘动态变化研究的基础,也是沙漠沙地景观响应于未来气候变化的重要指标之一[1]。关于沙丘潜在活性指标,Fryberger提出RDP/DP指标[2](总输沙势DP=U2(U-Ut)t/100,U和Ut分别是10 m高度处的风速和临界起动风速,t为观测期间大于临界起动风速的频率,RDP为合成输沙势),但输沙势只能表示大尺度区域潜在输沙能力,对于精确到单位像元的评估,其精确度不够。Lancaster提出沙丘潜在活性指标[3](M=W/(P/ET),W为每年超过起动风速的天数占全年的百分比;P和ET分别为年平均降水量和潜在蒸发量)将区域蒸散量、降水和风速作为主要变量表征沙丘潜在活性。由于该方法是根据美国东部湿润气候条件下的渗透计观测资料建立而成,与我国地形复杂、气候多变的西北干旱区自然条件差距甚大[4]。同时公式中对年潜在蒸散量的计算采用Thornthwaite的温度解析法[5],虽已给出完整的计算公式与应用实例,但作为主要变量的温度源自空气温度,并不是影响地表蒸散的直接原因,对大气蒸发的极端情况反映也不敏感,因而对于我国沙漠沙丘潜在活性评价是否适用有待考证。客观且中小尺度的评价沙丘潜在活性,需要综合考虑所涉及的诸多变量包括近地表沙土干燥度、下地表起伏度、植被覆盖度、近地表风速以及降水量等。就蒸散量而言,罗建等以Penman-Monteith公式为标准,对华北地区依据平均偏差、相关系数和t统计量等3种指标分别对温度法和辐射法估算蒸散量做出评价,认为辐射法整体上优于温度法[6]。表面能量平衡模型SEBS(Surface Energy Balance System)[7]是近年来应用较为广泛的利用辐射法估算蒸散量的方法之一,它根据地表能量平衡方程,利用卫星遥感影像收集到的近红外、可见光波段和热红外波段信息对大尺度区域范围的蒸散量进行反演计算,在高原地区遥感蒸发估算方面有较高精度[8]。因此本文以库布齐沙漠为例采用 SEBS模型代替 Lancaster的Thornthwaite方法估算蒸散量,并将年蒸散分为4部分代表4个季节计算,以提高蒸散量的精度;另一方面,各个变量对于沙丘潜在活性既有正相关又有负相关难以将多变量综合评价,因此本文考虑将模糊模型引入沙丘潜在活性评价中,结合地表粗糙度、NDVI、降水、风速等数据,通过模糊聚类与叠加提取各季节沙丘潜在活性指数的区域分异,最后给出潜在活性的新分级标准。
1 研究区域及数据来源
1.1研究区域概况
库布齐沙漠是我国八大沙漠之一,位于鄂尔多斯高原北部、黄河以南地区(图1)。呈东西向长带分布,其西、北、东3面均由黄河环绕,地势南高北低,东西长约400 km,南北宽15~50 km,面积约为1.87×104km2,占全国沙漠(沙地)面积的2.1%[9]。隶属内蒙古鄂尔多斯市的杭锦旗、达拉特旗和准格尔旗。该区大致以“包头—杭锦旗”一线为界,东部处于半干旱草原地带,西部属于半干旱荒漠(荒漠草原)地带。从地质地貌角度看,沙漠位于鄂尔多斯地台北缘,构造属鄂尔多斯台向斜。库布齐沙漠地势南高北低,由北向南依次分为三大地貌:北部为黄河河漫滩地,中部为风成沙覆盖的黄河阶地,南部为片状流动沙丘和灌丛相间的构造台地[10]。
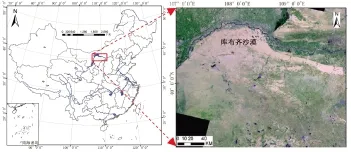
图1 研究区域位置
关于库布齐沙漠范围的界定,文献中的介绍尚不一致[10]。从自然地理的角度来讲,库布齐沙漠边缘与周围地区并无明确界限,加之各研究所依据的资料和量算方法不同,使得以往对库布齐沙漠范围的界定存有差异[11]。本文采用1980年Landsat MSS(空间分辨率80 m),1990年、2000年、2010年Landsat TM/ ETM+多光谱影像(空间分辨率30 m)图像解译数据并参照《中华人民共和国地貌图集(1:100万)》[12]以及实地调研得出30 a库布齐沙漠的地貌分类图,确定库布齐沙漠的平均范围以及各类型沙丘范围(图2)。
通过30 a遥感数据解译,库布齐沙漠风沙地貌总体特征是:风沙地貌类型与规模自西向东趋于简单。西部分布有抛物线形沙丘、格状沙丘、新月形沙丘及沙丘链、复合型沙丘等沙丘类型,而东部仅以新月形沙丘和灌草丛沙丘为主。
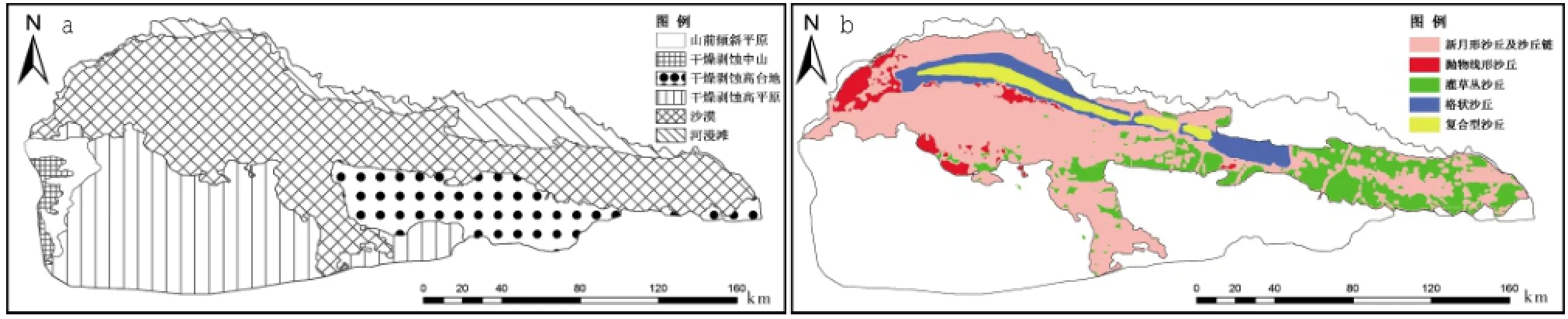
图2 库布齐沙漠地貌(a)与沙漠范围(b)
1.2数据来源及预处理
1.2.1遥感图像数据
采用NASA数据中心(http://modis.gsfc.nasa.gov/)提供的MODIS数据对2008年4月、7月、10月、1月中库布齐沙漠地区天气晴朗且无云的卫星图片进行研究。并且从中选取春(4月23日)、夏(7月12日)、秋(10月16日)、冬(1月7日)各一副遥感影像为代表进行数据分析,数据预处理主要包括几何校正、辐射定标、大气校正等。
1.2.2气象资料
获取2008年国家基础气象站中国地面气候资料(http://cdc.cma.gov.cn/home.do)中东胜、包头、呼和浩特、临河、鄂托克旗、伊金霍洛旗和杭锦后旗等国家气象站的气象数据并插值到整个库布齐沙漠以及NASA数据中心提供的气象数据。日期与遥感影像相对应,主要包括:2008年4月23日、7月12日、10 月16日、1月7日的日平均气压、日最大风速、日平均风速、日照时数、日臭氧含量、日水汽含量、日气溶胶光学厚度以及月平均降水量等气象资料。
1.2.3DEM
数字高程模型采用国际科学数据服务平台(http://datamirror.csdb.cn/)提供的库布齐沙漠地区30 m分辨率的SRTM-DEM数据。
2 研究方法
2.1地表能量平衡系统SEBS模型
地表能量平衡系统 SEBS(Surface Energy Balance System)模型是根据地表能量平衡系统估算地表蒸散量方法,即地球表面所获得的净辐射能等于土壤热通量、感热通量和潜热通量之和,该方法有较强的物理基础[13],其利用卫星遥感影像收集到的近红外、可见光波段和热红外波段信息对大尺度区域范围的蒸散量湍流显热通量;为湍流潜热通量;为汽化潜热;为实际水分蒸发总量。
2.1.1地表净辐射通量
净辐射通量是地球表面所获得的各种辐射之和,其计算公式如下:
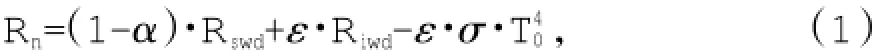
式中,α为反射率,Rswd为短波辐射,Riwd为长波辐射,ε为地表发射率,σ为Stefan-Bolzmann常数,T0为遥感观测的地表辐射温度。α、ε、T0可由遥感数据的可见光至热红外波段得到[14-18]。
2.1.2土壤热通量G0
土壤热通量是地表能量平衡方程中的一项,SEBS模型假定土壤热通量与净辐射及植被覆盖率的关系为[19]:
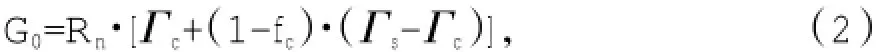
式中,Rn为净辐射通量;Γc为植被完全覆盖条件下土壤热通量与净辐射的比值;Γs为裸土条件下土壤热通量与净辐射的比值;fc为植被覆盖率,由下式计算:

式中,NDVI为归一化植被指数,其中NDVImin为裸地的NDVI值,NDVImax为植被完全覆盖区的NDVI值。
2.1.3显热通量H
在SEBS模型中,显热通量H是由“干限”和“湿限”的显热通量确定约束条件,通过求解一系列非线性方程得来的。为确定蒸发比,需先对极限条件下的能量平衡进行计算[20]。
在“干限”条件下,由于受土壤含水量的限制,蒸散量为0,潜热为0,显热最大:
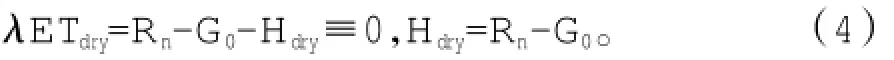
在“湿限”条件下,蒸散量仅受地表和大气条件所决定的蒸发能力约束,显热最小:
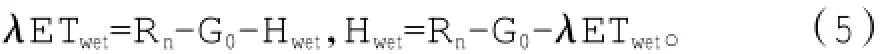
故相对蒸发率(relative evaporation)为:
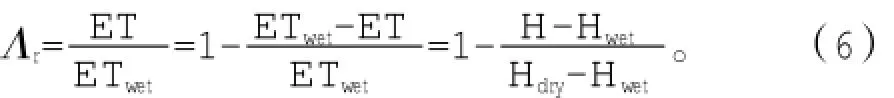
蒸发比(evaporative fraction)为实际蒸散与可用能量的比值,即:
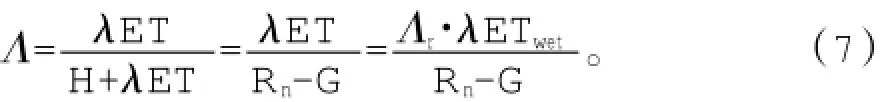
上述公式构成了SEBS模型的基础,通过求解“干限”Hdry和“湿限”Twet两种极端情况约束下的一系列非线性方程,可得到实际的显热通量[21-22]。
2.1.4瞬时蒸散与日蒸散
卫星遥感影像提供的是瞬时扫描的信息,所以SEBS模型只能计算瞬间的ET,然后通过蒸发比可将其转换计算为当天的蒸散量。公式如下[23]:瞬时的显热通量和潜热通量为:
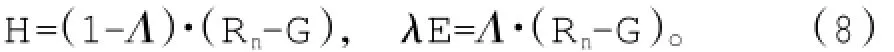
当蒸发比已知时,全天的蒸散量可由下式计算:

式中,ETdaily为全天的实际蒸散量(mm/d);Λ204为全天平均蒸发比,由于蒸发比守恒,SEBS可近λ是蒸发潜热(J/kg);ρw为水的密度(kg/m)。
2.2模糊评价模型
对于沙丘潜在活性的影响因素主要涉及近地表沙土干燥度、下地表起伏度、植被覆盖度、近地表风速以及降水量,其各沙丘潜在活性的影响方式(表1)。

表1 沙丘潜在活性影响因素
对于沙丘潜在活性评价,判断一个沙丘是高潜在活性还是低潜在活性,表1中变量并没有明确的判定界线,同时各个变量有正相关也有负相关且量纲不同,因此模糊评价模型的引入就解决了多因素综合的问题以及评价边界模糊的问题[24]。
模糊评价过程主要分为3步:①数据归一化;②模糊分类;③模糊叠加。将原始输入值变换为0~1的隶属可能性范围的过程称为归一化过程,也就是去量纲过程,模型中的每个条件都将被归一化,将变量中具体数值转变为相对两端极值的相对隶属度,也就是相对概率。
级别a与b构成对立模糊概念,根据对立统一定理[25]有:

式中:μ(iau)、μi(bu)分别为待评对象u指标i对级别a与b的相对隶属度。
设待评对象u指标i的特征值xi落入级别a与b相对隶属度为1的标准值区间[yia,yib]内,则xi对h级的相对隶属度为:

这里认为μi(au)、μi(bu)分别为沙丘潜在活性u(待评价对象)对于变量i最小值a与最大值b的相对隶属度。如果变量i相对于沙丘潜在活性为正相关,则i越大潜在活性越高,那么i对于沙丘潜在活性为“越大越优型”变量,采用模糊较大值模型(表1)进行模糊分类,对于μia(u)或μib(u),它距离1越近,其影响沙丘潜在活性的概率越高,相反影响越低,模糊较大值模型定义中点用于确定交叉点(分配的分类为0.5),大于中点的值成为集合1的概率较高,小于中点的值较低。同理如果为负相关,则i越小潜在活性越高,那么i对于沙丘潜在活性为“越小越优型”变量,采用模糊较小值模型(表1)进行模糊分类。当所有变量均转化为影响沙丘潜在活性的概率之后,将变量叠加求和,求出概率最大区域,该区域即为综合所有变量的影响最大的区域。

图3 库布齐沙漠日蒸散量(ET)季节对比(单位:mm·d-1)
3 研究应用
3.1日蒸散量(ET)估算
基于SEBS模型,利用瞬时潜热通量以及卫星过境瞬间提供的各个参量,通过计算得到蒸发比并通过日照时数等地表参数的引入,最终获得当天的实际日蒸发蒸腾量,蒸散量反演结果见图3。
蒸散量为地面上植物的叶面散发(蒸腾)与植株间沙土蒸发量之和[7]。反演结果表明,春季ET整体蒸散值适中(图3a),西部地区3.5~4.0 mm,东部及其边缘地区蒸散量较高,最大值接近5.0 mm;夏季ET值达到年最大值,由于气温上升,雨水充沛,植被茂密,沙土蒸发与植物蒸腾作用加强,除东部部分地区蒸散值较小外,其余大部分地区在5.0 mm以上,极值可达8.1 mm(图3b);秋季气温下降,降水减小,沙土蒸发与植物蒸腾作用均减弱,ET值也随之降低,东西部差异较为明显,西部ET值下降较快,平均在2.5~3.5 mm之间,东部相对较高,在4 mm左右;冬季ET值进一步降低,受气温的影响,一年生植物大量死亡,沙土蒸发能力达到一年中最弱,西部ET逐渐降至最低,不到1 mm,中东部相对较高但是整个库布齐沙漠蒸散量均较低。总之,时间尺度上库布齐沙漠一年内蒸散量呈“夏季>春秋季>冬季”的趋势,空间尺度上结合库布齐沙漠地貌分类图(图2)可知西部为沙漠腹地,多为流动沙丘,东部为灌草丛沙丘,植被覆盖度较高,年蒸散量东西部存在空间分异,全年普遍东部高于西部。
魏雅芬等[26]利用位于库布齐沙漠中部的涡度观测塔以及净辐射仪、时域反射仪、热通量板等设备测定净辐射通量、土壤热通量等参数并基于SEBS模型分析了库布齐沙漠年潜在蒸散量的变化特征(图4),文章指出库布齐沙漠潜在蒸散量有明显的季节变化特征,夏季蒸散量高,冬季低,整体趋势亦呈“夏季>春秋季>冬季”。
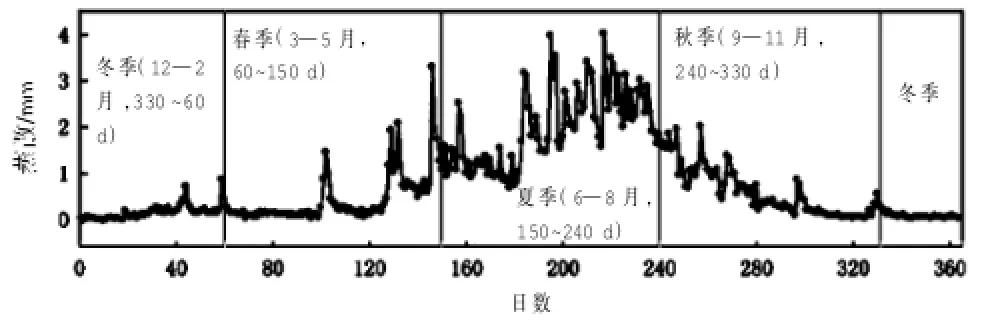
图4 库布齐沙漠年蒸散量变化[26]
卢娜等[27-28]也利用SEBS模型结合NOAA/AVHRR遥感影像数据,计算了鄂尔多斯北部盆地地表年蒸发量,文章认为鄂尔多斯盆地北部沙漠区蒸散量存在东西差异,其年蒸散量东部高于西部,究其原因主要是该区流动沙丘沙粒分选度高,透水性好,降水可迅速转换为地下水,而沙土水分在无降水时期,表层开始失水干燥,沙层毛管水断裂,表面形成较厚的干沙层[29],干沙层抑制了层下土壤水和地下水的蒸发,而蒸发量大的地区主要是在干湿沙层的界面进行,在地表面蒸发很小,因此西部流动沙丘蒸散量小于东部。
以上结论与本文用SEBS模型反演的蒸散量值在时间尺度的年内变化、空间尺度的分异变化以及其数值大小都具有较好的一致性,SEBS反演的2008年日蒸散量最大值也出现在夏季,且季节变化显著,空间差异显著。因此利用SEBS模型反演库布齐沙漠地区蒸散量具有一定的准确性,可以作为干旱区大面积蒸散量计算的一种有效方法。
3.2模糊M指标计算
根据Lancaster的M指标公式(M=W/(P/ET))来看,M值与ET值成正相关,因而蒸散值会决定M值区域分异,而沙丘潜在活性的区域分异不能完全由蒸散决定,应该结合近地表风力大小、地表粗糙度等多因素来综合评定。基于此本文提出“模糊M”指标,采用SEBS模型反演蒸散值来表征地表蒸发状况,并利用地表粗糙度和NDVI来表征下伏地面起伏状况和近地表风速状况,蒸散值越大地区,其沙丘移动较快,属于“越大越优型”;地表粗糙程度大的地区,地表对流动沙丘有阻碍作用,沙丘移动慢,因此粗糙度越小潜在活性越高,属于“越小越优型”;近地表风速用NDVI来表征,由于沙丘表面油蒿、沙柳等植被的存在削弱了近地表风速,沙土的吹蚀量减小,导致沙丘潜在活性降低,因此NDVI值较高区域,近地表风速小,沙丘整体潜在活性应较低,而无植被覆盖的流动沙丘,沙丘潜在活性较高,因此NDVI(近地表风速)属于“越小越优型”。
将ET值、地表粗糙度和NDVI三者进行模糊分类与叠加,计算出影响沙丘潜在活性概率最大的区域,具体过程为:首先利用ArcGIS10.1的Raster Calculator工具将ET值、地表粗糙度和NDVI进行归一化处理,公式为“(栅格数据-最小值)/(最大值-最小值)”,得到0~1分布的栅格数据;之后利用ArcGIS10.1空间分析中的Fuzzy Membership工具将归一化的ET值、地表粗糙度和NDVI进行模糊分类,ET值采用模糊较大值模型,地表粗糙度和NDVI采用模糊较小值模型求得相对概率;然后利用Fuzzy Overlay工具将模糊分类的3个条件进行模糊叠加,模糊叠加是要针对叠加模型中的多个条件分析所有集合之间的关系和交互,模糊叠加方法以集合论为基础,叠加方法选择Fuzzy Sum,它表示当组合栅格的重要性高于任何单个栅格时求得组合栅格的最大概率;最后结合季度风速与降水数据计算出的沙丘潜在活性分布,公式如下:
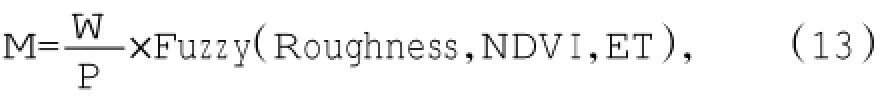
式中,M为沙丘潜在活性指标;W为每季度超过起动风速的天数占该季度总天数的百分比;P为季平均降水量;Roughness为地表粗糙度;NDVI为季归一化植被指数;ET为季潜在蒸散量;Fuzzy()为模糊分类与叠加模型函数。利用“模糊M”指标计算库布齐沙漠沙丘潜在活性的区域分异见图5。
结合库布齐沙漠平均四季降水、风速数据(图6),“模糊M”指标的春季沙丘潜在活性高值区位于沙漠西部,结合地貌分类图(图2)可知该地区包含大量新月形沙丘及沙丘链,植被相对较少,沙源较为丰富,同时该区域蒸散值较高且春季降水量较少可导致近地表沙土相对干燥,春季超过起动风速的日数为58 d,在多风、干燥、低植被覆盖的环境下西部地区沙丘潜在活性相对较高;低值区位于东部灌草丛沙丘地带,该区域沙流较少,植被生长状况较好,可削弱地表风速,同时大量沙子堆积于灌丛基部,导致沙丘被固定,最终使得东部灌草丛沙丘潜在活性较低。
夏季由于降水量增大,全季处于湿润状态,土壤含水量增多,沙子粘滞性和团聚作用加强,沙土不易被吹蚀,同时植被生长茂盛,相对春季风速变小,因此夏季整体沙丘潜在活性较春季变小。
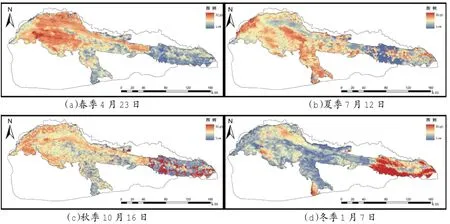
图5 库布齐沙漠“模糊M”指标四季分异
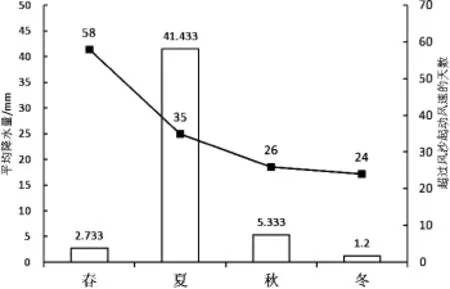
图6 库布齐沙漠四季平均降水与风速数据
秋季降水量减少,沙土干燥度增大,西部新月形沙丘及沙丘链、抛物线形沙丘等重新活化,东部灌草丛沙丘植被开始减少,近地表风速加大,沙土裸露导致东部沙丘潜在活性加大。
冬季由于气温降低,植被大量减少,东部灌草丛沙丘尤为明显,大量沙丘裸露,相比西部大型沙丘而言,裸露的灌草丛沙丘体积小、高度低,在高潜在活性下更易移动,因此冬季植被消亡后东部的灌草丛沙丘潜在活性反而增大,超过西部沙丘,沙漠西部沙丘中除部分处于沙漠边缘的新月形沙丘及沙丘链和抛物线形沙丘仍有潜在活性外,整体潜在活性均较小。
3.3模型对比与讨论
通过求取四个季度的蒸散平均值以及模糊模型平均值得到两个沙丘潜在活性公式年均结果。如图7所示,a为Lancaster[3]的年均M指标,b为年均“模糊M”指标。图8a中高值区位于沙漠中南部和东部,低值区出现在西部流动沙丘,因此M指标表征沙丘潜在活性为“东高西低”,与蒸散量空间分布一致;“模糊M”指标高值区主要集中于西部新月形沙丘及沙丘链、复合型沙丘、格状沙丘等,中东部相对较低,整体与M指标相反。
Lancaster[3]的M指标是主要依赖于气象参数获得的综合指标,仅涉及到蒸散、降水、风况,与Fryberger的输沙势一样是表征沙丘形变需要的外部动力条件,其高值区仅代表外部环境的对沙物质的迁移具有高的能量输送,而讨论潜在沙丘活性的真正驱动力,不仅需要外在环境的条件,沙丘本身的植被状况、下垫面的起伏度也是影响其形变的原因。模糊M指标综合了沙丘形变的内外影响因素,给出沙丘形变的综合驱动力,该驱动力直接导致了沙丘的移动,是沙丘移动和形变的潜在动力基础,即为沙丘潜在活性。因此沙丘实际移动状况和形变状况可以直观的反映沙丘潜在活性大小。
表2为基于库布齐沙漠1980—2010年Landsat MSS和TM/ETM+遥感影像30 a解译数据,通过GIS软件统计出各类沙丘的平均移动速度。由表可知库布齐流动沙丘移动速率相对较大,西部新月形沙丘及其沙丘链平均移动速率可达12.6 m/a;抛物线形沙丘为10.0 m/a,接近杜会石等[29]测定的11.69 m/a;格状沙丘及复合型沙丘由于结构复杂移动速度相对较缓,这与陈芳等[30]研究的结论相一致;灌草丛沙丘由于植被覆盖率较高,长时间被植被固定,近地表风速较弱,导致年均移动不明显,平均1.48 m/a,从沙丘的移动速度上看库布齐沙漠遵循“西高东低”,符合“模糊M”指标的空间分异。
3.4新分级标准与精度验证
结合像元频数分布直方图(图8),根据分布拐点将指标值分为5类:0~10;10~20;20~30;30~40;40~50,分别表示:极低潜在活性;低潜在活性;中潜在活性;高潜在活性;极高潜在活性。通过像元统计,库布齐沙漠由10%高潜在活性沙丘、40%中潜在活性沙丘和50%低潜在活性沙丘组成。

图7 库布齐沙漠两指标结果对比

表2 库布齐沙漠30 a主要沙丘类的平均移动速度/(m/a)

图8 “模糊M”指标像元直方图(a)与新分级标准(b)
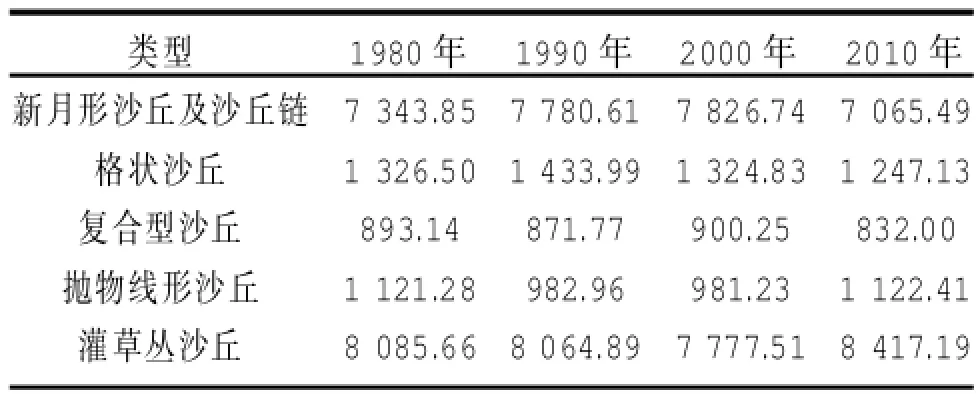
表3 库布齐沙漠30 a主要沙丘类型面积/km2
表3为库布齐沙漠1980—2010年各类沙丘的面积变化,其中灌草丛沙丘占总面积的42.9%,接近“模糊M”指标的低潜在活性沙丘比例,同时57.1%的新月形沙丘及沙丘链和抛物线形沙丘也接近沙丘潜在活性的中高值区,通过“模糊M”的像元统计和沙丘面积比例计算其精度为85.5%;相比M指标,利用Natural Breaks(Jenks)法分出相对应5类并结合沙丘面积计算其精度仅为60.4%,同比提高29.4%。由此可知“模糊M”指标在库布齐沙漠的空间分异特征以及数值大小都具有较好的一致性,可以作为计算沙丘潜在活性的一种有效方法。
4 结论
以库布齐沙漠为例采用 SEBS模型代替Thornthwaite方法估算蒸散量,并将年蒸散分为4部分代表4个季节计算,同时将模糊模型引入沙丘潜在活性评价中,结合地表粗糙度、NDVI、降水、风速等数据,提取各季节沙丘潜在活性指数的区域分异,最后与M指标进行对比分析得到如下结论:
(1)库布齐沙漠由10%高潜在活性沙丘、40%中潜在活性沙丘和50%低潜在活性沙丘组成。高潜在活性沙丘主要位于沙漠西部,包括少量新月形沙丘及沙丘链、抛物线形沙丘、格状沙丘以及复合型沙丘;中潜在活性沙丘包括其余大部分新月形沙丘、格状沙丘等;低潜在活性沙丘主要位于沙漠中东部,包括大量灌草丛沙丘以及植被覆盖率较高的新月形沙丘。高潜在活性的原因主要是近地表沙土较为干燥,植被覆盖率低,风沙地貌演变程度相对剧烈,中低潜在活性沙丘植被覆盖率高,近地表风速较低,沙丘相对固定。
(2)相比M指标,模糊模型更适用于沙丘潜在活性评价。通过模糊分类将各个条件变量转化为影响概率,再通过模糊叠加将多个条件变量结合,得到影响沙丘潜在活性的最大概率区域,经验证该区域包含沙漠西部新月形沙丘和抛物线形沙丘等,符合我国自然条件下的沙漠状况,同时也可揭示出气候—植被—沙丘(地形)的作用关系,因此“模糊M”指标更符合实际情况。
[1]Thomas D S G.Arid zone geomorphology:process,form Mand change in drylands[M].Wiley-Blackwell,2011.
[2]Fryberger S G,Dean G.Dune forms and wind regime[J].A Study of Global Sand Seas,1979,1052:137-169.
[3]LancasterN.Developmentoflineardunesinthe southwestern Kalahari[J].Journal of Arid Environments,1988,14:233-244.
[4]黄鹏展,阿部都热西提·阿布都外力,赵建平.沙丘移动的研究现状与未来研究思路 [J].沙漠与绿洲气象,2010,4 (1):1-5.
[5]Thornthwaite C W.Anapproachtoward a rational classificationofclimate[J].GeographicalReview,1948,38:57-94.
[6]罗健,荣艳淑.几种潜在蒸散量经验公式在华北地区的应用评价[N/OL].中国科技论文在线,2007.
[7]金晓媚,万力.Su Z B.遥感与区域地面蒸散量估算方法[M].北京:地质出版社,2008.
[8] 拉巴,除多,德吉央宗.基于SEBS模型的藏北那曲蒸散量研究[J].遥感技术与应用,2012,27(6):919-926.
[9] 钟德才.中国沙海动态演化[M].兰州:甘肃文化出版社,1998.
[10] 吴正.中国沙漠及其治理[M].北京:科学出版社,2009.
[11] 李朝生.鄂尔多斯高原北部沙区植被—环境关系与生态建设对策[D].北京:中国林业科学研究院,2005.
[12] 中华人民共和国地貌图集编辑委员会.中华人民共和国地貌图集[M].北京:科学出版社,2009.
[13]SandholtI,AndersenHS.Derivationofactual evapotranspiration in the Senegalese Sahel,using NOAAAVHRR data during the 1987 growing season[J].Remote sensing of environment,1993,46(2):164-172.
[14] 段爱旺,孙景生,刘钰,等.北方地区主要农作物灌溉用水定额[M].北京:中国农业科学技术出版社,2004.
[15]Parlange M B,Katul G G.Anadvection-aridity evaporation model[J].WaterResourcesResearch,1992,28(1):127-132.
[16]De Bruin H A R,Keijman J Q.The Priestley-Taylor evaporation model applied to a large,shallow lake in the Netherlands[J].Journal of Applied Meteorology,1979,18 (7):898-903.
[17]Menenti M,Choudhury B J.Parameterization of land surface evaporation by means of location dependent potential evaporation and surface temperature range[J]. 1993.
[18] 李新,黄春林,车涛,等.中国陆面数据同化系统研究的进展与前瞻[J].自然科学进展,2007,17(2):163-173.
[19] 刘绍民,孙睿,孙中平,等.基于互补相关原理的区域蒸散量估算模型比较[J].地理学报,2004,5(3):331-340.
[20]孙菽芬.陆面过程的物理、生化机理和参数化模型[M].北京:气象出版社,2005.
[21]Hill R J.Review of optical scintillation methods of measuring the refractive-index spectrum,inner scale and surface fluxes[J].Waves in Random Media,1992,2(3):179-201.
[22] 辛晓洲,田国良,柳钦火.地表蒸散定量遥感的研究进展[J].遥感学报,2003,7(3):233-240.
[23] 雷慧闽,杨大文,沈彦俊,等.黄河下游灌区水热通量的观测与分析[J].清华大学学报,2007,47(6):801-804.
[24]曹菡,陈军,杜道生.模糊边界地理现象的建模方法[J].西北大学学报:自然科学版,2001,2:108-114.
[25] 陈守煜,王子茹.基于对立统一与质量互变定理的水资源系统可变模糊评价新方法[J].水利学报,2011,42(3):253-261.
[26]魏雅芬,郭柯,陈吉泉.降雨格局对库布齐沙漠土壤水分的补充效应[J].植物生态学报,2008,32(6):1346-1355.
[27]卢娜,万力.基于RS的鄂尔多斯北部盆地地表蒸发量计算[J].地质通报,2008,27(8):1165-1167.
[28]卢娜.基于遥感的鄂尔多斯盆地蒸发量计算及植被指数分析[D].北京:中国地质大学,2006.
[29]李品芳,李保国.毛乌素沙地水分蒸发和草地蒸散特征的比较研究[J].水利学报,2000,03:26-30.
[30]杜会石,雷军,杨越.基于3S技术的库布齐沙漠抛物线形沙丘形态变化研究 [J].水土保持通报,2013,33(3):165-169.
[31]陈芳,刘勇.巴丹吉林沙漠典型地域沙丘多年变化的遥感动态分析[J].遥感技术与应用,2011,26(4):501-507.
Evaluation of Dunes Potential Activity Based on Improved M Index:A Case Study of Hobq Desert
GUAN Chao,HASI Erdun,TAO Binbin,LIU Dan,ZHOU Yanguang
(College of Resources Science and Technology,Beijing Normal University,Beijing 100875,China)
That quantifiable assess of the dunes activity is essential of the dynamic research of desert.At present,using the index M(M=W/(P/ET))given by Lancaster is a primary study method of dunes activity.However,considered complicated landforms and variable climate,especially in the arid environment in the northwest of China,this method has great gap to the actual situation.Taking the Hobq Desert as an example,we replace SEBS model of Thornthwaite model to calculate the surface evapotranspiration.In order to improve accuracy we classified the annual evapotranspiration into four parts based on four seasons.Meanwhile taking advantage of the fuzzy model containing a range of factors,such as surface roughness,NDVI,precipitation,wind speed and other data,we extracted the regional differentiation of dunes activity index in those seasons.Finally,combining with geomorphologic map,we complished a new activity grading standard.It has been proven that this model standard,based on fuzzy model can composite a series of influence factors,is gearing to China actual situation.In a word,the fuzzy model improves the accuracy of assessment and the Lancaster’s M Index is not suitable for China.
dunes activity;SEBS model;fuzzy model
X144
B
1002-0799(2016)03-0021-09
10.3969/j.issn.1002-0799.2016.03.004
2015-03-06;
2015-04-25
国家自然科学基金“抛物线形沙丘的动态变化研究”(41171002);国家“十二五”科技支撑计划项目(2012BAD16B0202)。
管超(1989-),男,博士研究生,主要研究方向:干旱区研究与地理数值模拟。E-mail:gc471603869@126.com
