最优组合预测方法在中长期电力负荷预测中的应用

夏耀杰（上海电气中央研究院，上海 200070）

最优组合预测方法在中长期电力负荷预测中的应用

夏耀杰
（上海电气中央研究院，上海 200070）

根据单一模型建立2种综合模型，分别为以减少拟合残差为目标的综合最优拟合模型和以提升预测能力为目标的综合最优预测模型。综合最优拟合模型采用二次规划算法对单一模型库进行与历史数据方差最小为目标的权值分配，然后在综合最优拟合模型的基础上以提升预测能力为目标的再次权值规划得到综合最优预测模型。通过综合最优拟合模型建立的综合最优预测模型不但在最大程度上接近历史变化规律，并弥补拟合模型在发展趋势上的不足。综合最优预测模型使用误差分析方法对文中所用模型进行分析、比较以区别模型优劣性，最后应用实际的算例，比较确定综合最优预测模型的有效性。

中长期负荷预测；单一预测模型；误差分析；最优组合预测

中长期电力负荷预测是以数理统计知识为理论基础，通过分析研究大量历史数据为实践基础，以科学的方式对历史数据进行建模并运用模型估计未来的走势。中长期电力负荷预测的主要工作是研究部门或地区的电力和电量消费历史情况及估计未来的变化发展趋势。中长期电力负荷预测的含义：对未来需求量（功率）的预测和未来用电量（能量）的预测［1］。本文对负荷预测分析思路紧紧贴合以上概念对未来用电量做预测。

影响负荷预测精度的高低有许多因素，理想的理论情况下应考虑其所有影响因素才能做到准确全面，但是实际情况又不允许将所有因素考虑进去，如何能准确、科学、可靠地预测负荷需要更深入研究其内在组织关系。目前用于负荷预测的方法很多，笔者根据电力负荷预测方法的研究对象不同，分为了自相关预测方法和互相关预测方法2类。其中自相关方法主要研究历史负荷数据本身的规律；互相关方法是从负荷影响因素入手，通过相关因素变化推测负荷变化。自相关模型有如灰色模型通过历史数据建立微分方程［2］；灰色马尔科夫方法则是通过马尔科夫修正灰色模型偏差［3］；增长曲线法是由S型曲线演变发展而来［4］；神经网络法因为其在非线性系统中的优势将其应用于负荷预测有良好的效果［5］；支持向量机是建立在结构风险最小和统计学的相关理论［6］。在互相关方法中主要有分行业法和弹性系数法［7—8］。分行业法的主要思想是将社会十大行业的用电量叠加，即分摊预测，最后总和得出总用电量；弹性系数法主要是通过研究经济与电力的关系，通过预测经济增长率和未来弹性系数来确定未来用电量。

目前多样性作为衡量预测模型是否具有适应能力的一个重要依据，已经被很多学科预测者所普遍认可。因为预测模型实际上是在相关拟定条件下运行，需要预测的事物本身就包含了许多相关、时变因素，其本质上是复杂且多元的，若使用单一预测模型就无法充分考虑预测模型的多样性，在预测精度上往往也难以有令人信服的结果，故多种预测模型的结合应运而生。

为得到适应性更好的负荷预测模型，本文提出一种最优组合模型。在已经建立单一模型的基础上通过4种权值规划算法得到综合最优拟合模型，分析4种规划算法下的最优拟合模型，最后根据综合最优拟合模型外推所得的结果规划得出综合最优预测模型。

1 综合预测模型理论介绍

1.1 综合最优拟合模型

设定综合最优拟合模型的目标为探寻一组权值，这组权值使得该模型所得残差尽可能小。其数学模型可表示为

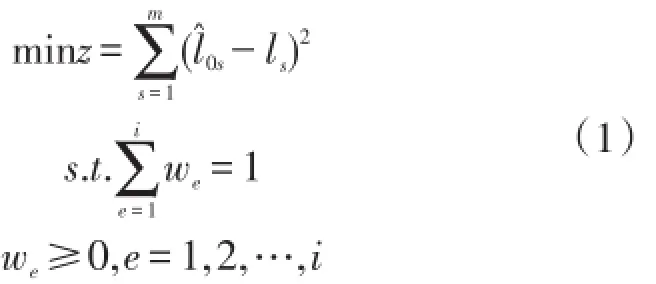
对式（1）进行展开

将拟合方差、拟合协方差代入式（2）得

记

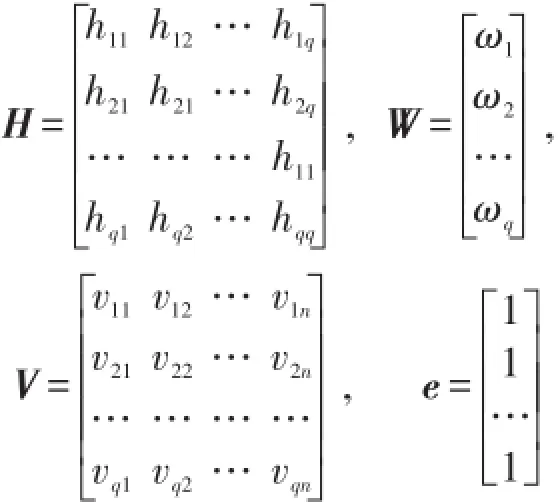
则

记

得

最终的如下二次规划模型

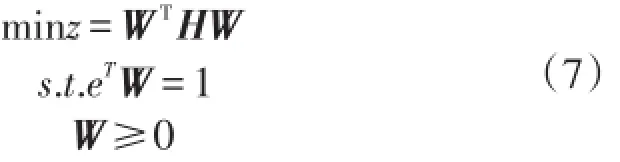
1.2 综合最优预测模型

上述模型试图寻找一种在拟合程度上的最优：通过在选定的几个单一模型中变化权值找到一个以残差最小为目标的综合模型。值得说明的是，对于某种非组合的模型，它对历史把握程度与外推能力之间没有硬性的关联，某个模型残差小于其他模型并没有说明其估计能力也一定突出。对于综合模型也是这样，虽然综合模型比单一模型更具多样性，但是终究也无法保证通过提升拟合精度就一定能对预测精度有所优化。正是这些理念，1.1节才取名为最优拟合模型，而不是最优模型，为了区分出模型只是单纯追求拟合的最优。

而对于录入模型库的单一预测方法，能否有一组权重在考虑拟合的同时也可以对其预测准确度有所考量。

在实际的建模中有2点值得考虑。

（1）为了做好预测，首先要立足于对历史规律的把握。1.1节中的“综合最优拟合模型”恰好是最好把握了历史规律的综合模型。类似地，如果另外一些综合模型能够达到比较好的拟合效果（次优），则也表明其在很大程度上已经把握了历史规律，可称之为“综合次优拟合模型”。如果某个预测模型对历史数据的拟合效果很差，则表明它没有把握历史规律，因此就无法用于预测。

（2）由于物理量发展变化规律的波动性和随机性，未来的变化趋势可能在一定程度上遵循历史规律，但并不是完全按照历史规律来发展。因此，那个理论上把握了历史规律第一的“综合最优拟合模型”，和那些对历史规律把握并不是最好的“综合次优拟合模型”，还是有机会在概率意义上得到最优解。

由此提出综合最优预测模型。

综合最优预测模型的确定，可归结为求取拟合程度唯一最优及若干次优的综合模型的再组合，即重新规划权值。

首先需要对历史进行时段划分，如图1所示。

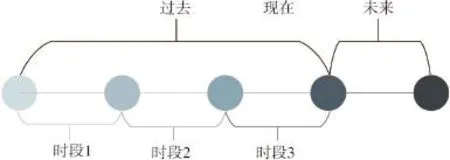
图1 历史样本时间段划分

预测模型只能用历史数据来检验其模型优劣性，故对历史数据进行3个阶段划分，时段1表示单一预测模型以及最优拟合模型利用时间段；时段2表示最优预测模型利用时间段；时段3用于最优预测模型误差分析。

假设由时段1所得 p个综合拟合模型y1，y2，…，yp。其中包含一个综合最优拟合模型和p-1个并不是最优但也是拟合程度较单一模型好的次优模型。其中各个综合预测模型包含有q个单一预测模型。假定第j个（j=1，2，…，p）综合预测模型内包含的q种单一预测模型的权值系数为ω，ω，…，ω。为每个综合预测模型引入权重系数σj，得综合最优预测模型

与求解最优拟合模型权值相似，设置综合最优预测模型的目标为取得一列权重，目的是得到的综合预测模型与实际情况尽量接近，即各个综合拟合模型在时段2的预测误差方差和最小。设时段2预测数据为n个，其数学模型可表示为

推导过程与最优拟合模型一样，这里不再重复。最后得二次规划式

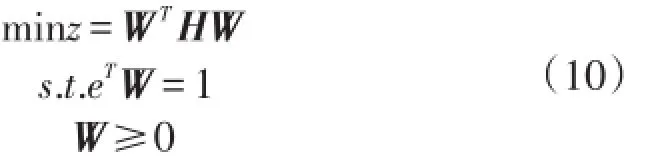
1.3 权值规划算法

小节1.1和1.2中的模型是以权值作为决策变量的非线性规划问题，可以应用相应的非线性规划方法求解。目前用于二次规划算法主要有智能算法，如：遗传算法［9］和粒子群算法［10］；经典算法，如：内点法［11］和直接搜索法［12］。本文应用这4种算法进行规划。

2 建模及算例分析

2.1 样本分析及划分

原始样本选取S市1986年至2013年全社会用电量，数据来源于电网公司统调数据。其中1998年至2010做训练样本，2011年至2013年做预测误差分析样本。1986年至2013年样本结构如图2所示。

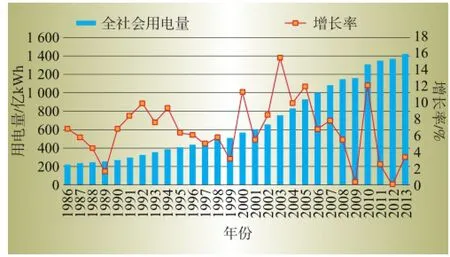
图2 全社会用电量及增长率

由图2可见，2013年S市全社会用电量为1 410 亿kWh，是1986年的555.8%，28年年均增长率为6.3%。其中2003年增长率最高，为15.38%，增长率最低的是2012年，仅为1.03%。增长率曲线除几处有较大波动外整体趋势平稳，并未出现负增长。

由1.2节中时间段划分规则对样本数据进行划分，将样本数据共划分为3段，分别是拟合模型时间段（1986年—2005年）、预测模型时间段（2006年—2010年）、模型校验时间段（2011年—2013年）。划分图示如图3。

图3 样本数据划分

在拟合模型时间段，首先建立单一预测模型库，根据最优拟合准则应用权值规划算法得出综合最优拟合模型。

运用上述综合最优拟合模型预测2005年至2010年全社会用电量，并根据实际数据进行最优权值规划，获得一组权值，此权值即为最优预测模型权值。

将最优预测模型应用于模型校验时间段，分析模型优劣。

2.2 S市综合最优拟合模型

为方便叙述，将选用的12种单一预测模型进行编号，如表1所示。

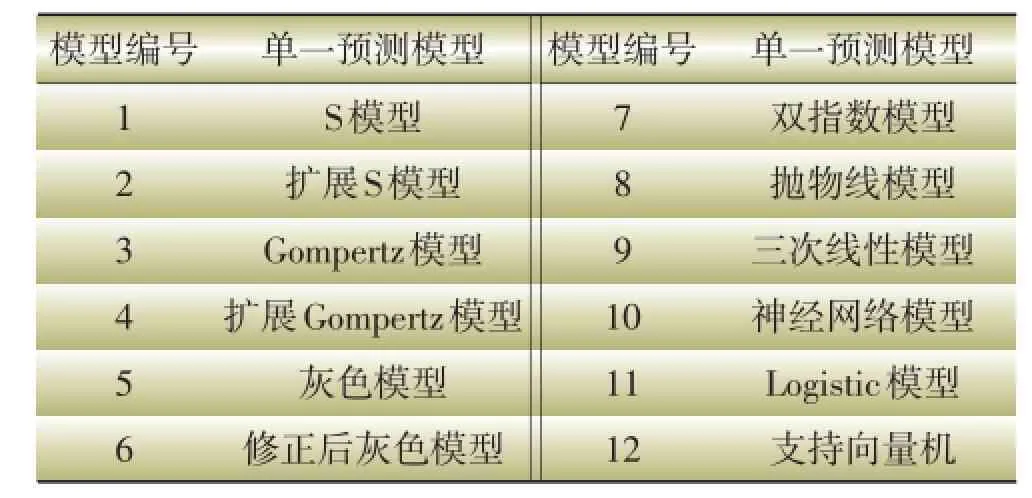
表1 单一模型编号

进行建模和预测之后，12种单一预测模型拟合精度及预测精度如表2所示。

表2 单一模型拟合误差和预测误差

表2中拟合误差是指各模型1986年至2005年拟合值与实际值的相对误差，预测误差是各模型所得2006年至2013年预测值与实际值误差。

由单一模型拟合值与历史样本值得12组残差，将小节1.3中权值规划算法用于这12组残差的规划，通过设置各综合模型迭代次数、运行时间等参数（例如：每个模型运行5次并取综合残差最小的那组比重作为模型权值）使得智能算法在精度上相近，其中遗传算法参数设置为采用二进制编码，初始化参数设置为：最大进化代次数取10 000；交叉概率取0.8，最大交叉概率为0.99，变异概率取0.01，种群大小为5 000，当达到最大进化代数时，终止程序。粒子群算法参数设置为：粒子数5 000，最大迭代次数10 000，学习因子一和学习因子二都为2，惯性权重为0.7。最后得综合最优拟合模型，所得权重如表3所示。

为简化叙述设定由遗传算法所得为综合模型一，由粒子群法所得为综合模型二，由直接搜索法所得为综合模型三，由内点法所得为综合模型四，由各规划算法得出综合模型的平均相对拟合误差和平均预测精度如表4所示。

表3 单一模型权重单

表4 综合拟合模型预测结果误差

4种规划模型所得拟合结果均优于单一模型，这是毋庸置疑的，因为综合模型组合目的就是寻求拟合结果最优，而最终结果中除了综合模型三，其他模型的结果在单一预测模型中只是处于上游，并无突出表现。这也说明拟合结果好，并不能代表预测结果就好。所以需要考虑这4个综合拟合模型的对未来把握的能力。

值得说明的是本文之所以用4个权值规划算法分别对12个单一模型进行计算，得出4种综合拟合模型，是因为规划算法的结果是由其模型参数和算法本身的特质所决定。故某种算法优于另一种算法这种说法是带有局限性的，本文运用4种算法是为了提供4种不同规划算法下的综合拟合模型。在笔者看来因为在实际规划算法中，某一权值算法虽然每次运行结果会有不相同，但是其权重分布概率是相差甚少的，例如：粒子群算法若是参数相同，多次运行后其分配给第10号单一模型的权重只是在千分位上变换，对整体权重布局并没有多少改变。正是基于这个原因，本文使用4种权值算法目的是在权值分布概率上的具备多样性。

2.3 S市综合最优预测模型

在2.2节中，12个单一模型通过权值规划算法得到4个拟合模型，现在由这4个模型的预测序列，即预测2006年至2010年的S市全社会用电量，所得预测值与原始值得出残差序列，对这4个预测残差序列进行权值规划，规划结果如表5。

表5 综合预测模型预测结果误差

综合模型预测结果指标如表6所示。

表6 综合预测模型预测结果误差

由于拟合的时间长短不一样，最优拟合模型和单一模型使用20年数据作为拟合，而最优预测模型实际上使用25年数据作为拟合，故用上述的最优拟合模型和单一预测模型无法科学、准确比较最优预测模型优劣。为直观比较最优预测模型的优劣性，本文将单一模型和最优拟合模型时间段延长至25年，延长时间段后最优拟合模型结果如表7所示。

表7 以25年为拟合的综合拟合模型预测结果误差

综合最优预测模型中平均拟合误差是指该模型1986年至2010年段共25年的平均误差，平均预测误差是指2011年至2013年段共3年的平均误差。从拟合角度看，综合最优预测模型在综合模型中并不突出，略劣于综合拟合模型。主要是因为预测模型不以拟合最优为主要目标，并且预测模型主要为了趋近2005年至2010年的负荷曲线。换句话说就是在预测模型25年的拟合时间段内，使得最优预测模型在局部上（2005年至2010年）优于最优拟合模型，而在其他部分上（1986年至2005年）劣于最优拟合模型，这也是由于最优预测模型的侧重点是针对最优拟合模型在2005年至2010的预测值进行规划。从预测误差来看，最优预测模型无论在综合模型还是单一模型中都是最好的，模型结果证明了综合最优预测模型的有效性。

3 结论

综合最优拟合模型是以拟合残差最小为目标而对若干单一模型进行规划；综合最优预测模型是由综合最优拟合模型所得预测值以预测误差最小规划而得，综合最优预测模型因为包括综合最优拟合模型，使得其既考虑了历史规律，又考虑了预测精度，真正做到拟合和预测兼顾。综合模型有单一模型所不具备的一个特点，即多样性。电力负荷本身受复杂的影响因素制约，建立模型就是对负荷趋势的一种模拟。单一模型由于自身局限性往往只能反映负荷影响因素的某些方面，而综合模型则能囊括这些影响因素，在模型特性方面能反映负荷较多特点，而这些特点是提高模型预测准确性的重要一环。

［1］ 康重庆，夏清，张伯明.电力系统负荷预测研究综述与发展方向的探讨［J］.电力系统自动化，2004（17）：1-11.

［2］ 邓聚龙.灰理论基础［M］.武汉：华中理工大学出版社，2002.

［3］ 夏耀杰，程浩忠.基于改进灰色马尔科夫预测法的中长期负荷预测［J］.电力需求侧管理，2015（1）：21-25.

［4］ 康重庆，夏清，刘梅.电力系统负荷预测［M］.北京：中国电力出版社，2007：1-20.

［5］ K B Sahay，M M Tripathi.Day ahead hourly load and price forecast in ISO New England market using ANN［C］∥India Conference（INDICON），2013 Annual IEEE，2013，1：1-6.

［6］ Jain Satish.Integrated approach for short term load forecasting using SVM and ANN［C］∥ENCON 2008-2008 IEEE Region 10 Conference，2008，1：1-6.

［7］ 唐良艳.电力系统负荷特性分析与负荷预测研究［D］.广州：华南理工大学，2010.

［8］ 吴安平.产业电力弹性系数的意义及其在负荷预测中的应用［C］∥中国电机工程学会电力系统规划学术会议论文集，1998：41-44.

［9］ Khandani F，Soleymani，S Mozafari.Optimal placement of SVC to improve voltage profile using hybrid Genetics Algorithm and Sequential Quadratic Programming［C］∥Electrical Power Distribution Networks（EPDC），2011 16th Conference on，2011.

［10］ Jain A，Srinivas E.A novel hybrid method for short term load forecasting using fuzzy logic and particle swarm optimization［C］∥Power System Technology（POWERCON），2010 International Conference on，2010.

［11］ 刘明波，王晓村.内点法在求解电力系统优化问题中的应用综述［J］.电网技术，1999，32（8）：61-64.

［12］ 江翠.无约束优化的分式插值直接搜索法［D］.南京：南京航空航天大学，2013.

（本栏责任编辑 管永丽）

Application of the optimal combined forecasting method in mid-long term power load forecasting

XIA Yao⁃jie
（Shanghai Electric Central Research Institute，Shanghai 200070，China）

This paper builds two synthetic models according to single model，one is combination optimal fitting model in order to reduce the fitting residual error as the goal，the other is combination optimal prediction model in order to increase forecasting ability.The optimal fitting model uses two-times programming algorithm to assign the weights of the single model base and the minimum varince of historical data.Based on the optimal fitting model，the weight program in order to increase forecasting ability is set to get prediction model.The model is maximum close to the law of historical data change，and makes up the deficiency of the fitting model in the development trend.Error analysis method is used to compare the advantages and disadvantages between the models.At last，through the actual example，the effectiveness of synthetic optimal forecasting model is compared and confirmed.

mid-long term load forecast；single forecasting model；the error analysis；optimal combined forecasting method

夏耀杰（1989），男，上海人，硕士研究生，从事电力系统规划方面的研究工作。

TM715

A

10.3969/j.issn.1009-1831.2016.04.004

2016-04-27；修回日期：2016-06-08

上海市科学技术委员会科研计划（课题）（14D Z120340）