泥石流灾害防治方案优选模型

2016-08-15王念秦曹红丽杨盼盼

中国水土保持 2016年8期

关键词：欧氏泥石流灾害

王念秦，曹红丽，杨盼盼

(西安科技大学地质与环境学院，陕西西安 710054)

泥石流灾害防治方案优选模型

王念秦，曹红丽，杨盼盼

(西安科技大学地质与环境学院，陕西西安 710054)

泥石流；评价指标；熵权决策法；比选模型

以陕北府谷三道沟矿区泥石流灾害防治工程为例，选取安全可靠性、环境协调性、经济合理性、设计规范性、施工复杂性、后期维护性等评价指标，提出基于熵权决策法的定量因素权重确定方法，建立泥石流防治方案比选模型。通过专家打分法建立原始判断矩阵，利用熵权法得到的熵值与属性矩阵确定理想矩阵，根据汪氏贴近度及欧氏贴近度计算待选方案评价指标与理想矩阵的贴近度来确定方案的优劣次序。结果表明，方案三(消能坝+Ⅰ型排导渠+停淤场)为最优方案。该比选模型在传统主观定性确定权重基础上定量确定评价指标权重，克服了权重确定主观随意性，提高了计算过程与结果的客观性及准确性，具有一定的理论意义和应用价值。

泥石流暴发危及交通、水利、矿山工程及群众生命财产安全，并造成巨大经济损失。为了解泥石流运动规律、制定防治措施、减轻灾害损失，许多学者进行了大量研究，比如：王念秦等[1]以影响泥石流灾害活动的因素为评价因子，定量确定预判范围及精度，建立泥石流灾害三级空间预测模型，还采用基于多级模糊综合评判的理论与方法建立了泥石流灾害易发性综合评判模型；匡乐红等[2]、刘勇健等[3]基于粗糙集理论对泥石流灾害进行危险度评价及区划，运用粗糙集理论获取评价指标的相对重要度，再依据专家经验确定主观权重，结合相对重要度和主观权重确定各因素的最终权重。在上述研究成果的基础上，为克服专家经验的差异性，引入模糊数学理论，以陕北府谷三道沟矿区泥石流防治工程为例，根据安全可靠性、环境协调性、经济节约性、设计规范性、施工难易度、后期维护性等评价指标，在传统主观定性确定权重的基础上提出基于熵权决策法定量确定评价指标权重的方法，建立泥石流防治方案比选模型，定量确定方案的比选过程，在探索泥石流防治方案方面是一次有益的尝试。

1　熵权决策法

熵权决策法是一种客观赋权方法，在没有专家权重的情况下，根据评价对象的指标值构成的判断矩阵来确定指标权重，克服经验确定指标权重的主观随意性[4-7]。设有m个待评方案、n项评价指标，形成原始指标数据矩阵R=(rij)m×n，rij为第j个指标下第i个方案的评价值，综合考虑多名专家意见确定。

第j个指标下第i个方案的指标值比重为

(1)

第j个指标的熵值为

(2)

式中：k=1/lnm。

第j个指标的熵权为

(3)

由式(3)知，指标熵值越大，熵权越小，说明该指标越不重要。当待选方案在指标j上的值完全相同时，该指标的熵值达到最大值1，熵权为零，表明该指标未能向决策者提供有用信息，即在该指标下所有的待选方案对决策者说是无差异的，可考虑去掉该指标。因此，熵权本身并不表示指标的重要性，而是表示在该指标下对评价对象的区分度。当评价对象确定后，决策者可根据熵权对评级指标进行调整、增减，以便做出更加可靠、精确的评价。

2　方案比选

(1)确定待选防治方案m个，影响方案比选结果的评价指标n个，根据第j个指标下第i个方案的评价值rij确定原始指标数据矩阵R。

(4)

(3)根据式(1)、(2)及标准化的矩阵R′得到各评价指标的熵值ej。

(4)根据熵值ej及矩阵R′，得到属性矩阵D,即

(5)

(5)通过属性矩阵D得到理想点矩阵A=(a1，a2，…，an)，其中aj=max{dij}(i=1，2，…，m)。

(6)设A、D是论域U上的两个模糊子集，故各待选方案可依据属性矩阵D与理想点矩阵A的距离进行比选，由于用距离来刻画模糊子集的模糊度需要做烦琐的计算，为弥补其不足，这里使用汪培庄教授[8]提出的贴近度(汪氏贴近度)来度量模糊性,即

(6)

式中：A·D与A×D分别表示A、D的内积与外积。

(7)计算属性矩阵中各待选方案在各评价指标下的评分值矩阵Di(i=1，2，…，m)与理想点矩阵Ai(a1，a2，…，an)的欧几里德贴近度(欧氏贴近度)，贴近度越大，越接近理想方案，即最优防治方案。

3　工程实例

3.1工程概况

三道沟矿区位于陕西省府谷县，处于以侵蚀为主的黄土梁峁区，地形破碎，沟壑纵横。区域内沟道纵横，地表水系较发育。煤矿开采会引发采空区塌陷和沟床变形、裂缝，为地表水提供了良好的下渗通道，一旦汛期形成洪水，对矿井安全极其不利。同时，大(柳塔)石(马川)公路建设正在沟道内施工，产生了大量的弃土弃渣，有形成泥石流灾害的潜在危险。按照府谷三道沟井田85201—85202开采工作面红石墕沟沟道地表水防治的指导思想和拟定的总体治理、设计原则，拟采用拦挡、疏排措施，让洪水尽可能少地入渗地下，并快速通过开采塌陷区，以达到防止矿井开采期间地表水淹井灾害发生的目的。依据矿区地理位置、水系分布、物源组成和性质等因素，设计4种临时防护工程方案：方案一，消能坝+Ⅰ型排导渠+护坡；方案二，消能坝+Ⅱ型排导渠+护坡；方案三，消能坝+Ⅰ型排导渠+停淤场；方案四，消能坝+Ⅱ型排导渠+停淤场。

防护方案中，在85202开采工作面对应沟道上游设置一道消能坝，以降低洪水通过工作沟道时的流速、冲击力及冲刷能力；在流通区修筑护墙，稳固岸坡滑塌；在堆积区修建停淤场，避免堵塞河道。在消能坝以下采用“单层刚性基础+双层柔性防渗中间层+刚性面层”结构排导渠工程(Ⅰ型排导渠)时，具体结构形式为采用单层角钢网片(或钢筋网片)构成单层刚性基础、两层沙袋间夹高强度防渗土工布构成双层柔性防渗中间层、铺设15 cm C15砼作为刚性面层。在消能坝以下采用“双层刚性基础+双层柔性防渗中间层+刚性面层”结构排导渠工程(Ⅱ型排导渠)时，具体结构形式为采用两层角钢网片(或下层角钢网片，上层钢筋网片)构成双层刚性基础、两层沙袋间夹高强度防渗土工布构成双层柔性防渗中间层、铺设30 cm M7.5浆砌块石作为刚性面层。

3.2防治方案比选

针对影响防治方案因素的复杂性，以安全可靠性、环境协调性、经济合理性、设计规范性、施工复杂性、后期维护性等作为评价指标，综合专家意见确定各指标在各待选方案下的评分值(表1)。

表1　待选方案评价指标评分结果

由表1确定原始指标数据矩阵为

(7)

标准化后的矩阵为

(8)

根据式(1)、(2)得到各评价指标的熵值(表2)。

表2　评价指标熵值

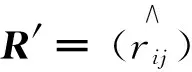
(9)

理想点矩阵A=(0.676 1，0.765 2，0.765 4，0.788 7，0.728 2，0.728 7)。根据式(6)计算各指标属性矩阵与理想点矩阵的汪氏贴近度(表3)。

表3　待选方案汪氏贴近度

由表3知，方案三与方案四贴近度一致，故方案三与方案四均可作为该矿区泥石流灾害的防治方案，但为了确定最优方案，利用欧氏贴近度NE[8]在两方案中比选最优方案，计算公式为

(10)

计算得到，方案三的欧氏贴近度为0.672 4，方案四的欧氏贴近度为0.561 7。故综合汪氏贴近度与欧氏贴近度计算结果，按照待选方案的优劣从大到小排序依次为方案三、方案四、方案二、方案一。

4　结　语

(1)熵权决策法是一种客观赋权方法，根据评价对象的指标值构成的判断矩阵来确定指标权重，克服了经验确定指标权重的主观随意性，保证了计算过程与结果的客观性及准确性，是一种定量表征评价指标权重的方法。

(2)为有效防治泥石流灾害，采用了基于熵权决策法的定量确定影响因素权重方法，通过多专家意见确定的指标评分值建立的原始判断矩阵及利用熵权法得到的熵值与属性矩阵确定的理想矩阵，根据汪氏贴近度及欧氏贴近度原理计算待选方案评价指标与理想矩阵的贴近度来确定方案的优劣次序，建立泥石流防治方案比选模型，定量确定方案的比选过程。

(3)结果表明，方案三(消能坝+Ⅰ型排导渠+停淤场)为最优方案，能够达到设计目的。目前，该矿区已按方案三进行治理，治理效果良好，社会效益和经济效益明显，证明了本研究成果的精确度，也说明模糊数学决策法是一种可行、定量的泥石流综合治理方案比选方法。

[1] 王念秦,薛瑶琼,李少兵,等.基于粗糙集理论的泥石流易发性综合评判模型[J].水土保持研究,2014,21(3):246-250.

[2] 匡乐红,徐林荣,刘宝琛,等.基于粗糙集原理的泥石流危险度区划指标选取方法[J].地质力学学报,2006,12(2):236-242.

[3] 刘勇健,刘义建.基于粗糙集的范例推理在泥石流危险性评价中的应用[J].山地学报,2008,26(2):223-229.

[4] 邱苑华.管理决策与应用熵学[M].北京:机械工业出版社, 2002:15-43.

[5] 陈瑞,王士革,盛才余,等.泥石流防治工程方案优化设计专家系统初步研究[J].自然灾害学报,1999(3):111-116.

[6] 闫文周,顾连胜.熵权决策法在工程评标中的应用[J].西安建筑科技大学学报,2004,36(1):98-100.

[7] 罗君君.熵权决策法在公路工程评标中的应用[J].佳木斯大学学报：自然科学版,2007,25(1):28-30.

[8] 李士勇.工程模糊数学及应用[M].哈尔滨:哈尔滨工业大学出版社,2004:70-75.

(责任编辑李杨杨)

国家自然科学基金项目(41572287，40972174)；国家自然科学基金重点项目(41130753)；陕西省科技统筹创新工程计划项目(2013KTCL03-15)；陕西省煤田地质局科技计划项目(JB2014-4)

S157.1