改进的偏最小二乘法在青海省农业用水预测中的应用

王　洁,章恒全

(河海大学商学院,江苏 南京　211100)



改进的偏最小二乘法在青海省农业用水预测中的应用

王洁,章恒全

(河海大学商学院,江苏 南京211100)

摘要：根据2000—2009年影响青海省农业用水的11个因子的基础数据,建立偏最小二乘回归模型,考虑到模型的实用性和准确性,运用后退法对偏最小二乘法进行改进,剔除了5个不需要的变量,得到了拟合精度更高的结果。选取2010—2013年数据进行模型检验。结果表明:运用偏最小二乘法预测的结果与实际情况贴近,并且改进的模型的贴近度更高。通过模型的应用,可以看到偏最小二乘法在青海省农业用水预测中有较好的应用价值,并且改进后的偏最小二乘法简化了模型,提高了预测精度,为青海省的农业用水预测提供了依据。

关键词：农业用水;用水预测;改进的偏最小二乘法;青海省

水资源问题是整个人类社会面临的一个严峻的问题,中国作为世界第一人口大国,水资源问题尤为严重,人均水资源可利用量为2 200 m3,仅为全球平均水平的1/4[1]。青海省位于青藏高原东北部,是长江、黄河、澜沧江和黑河的源头,是我国重要的水源地,素有“中华水塔”之称。青海省水资源总量相对丰富,2013年全省的平均降水量为298.8 mm,水资源总量为645.60亿m3,其中地表水资源量为629.55亿m3,地下水资源量为290.77亿m3。但其水资源存在较强的季节性和地域性,全年降水主要集中在6—9月份,且降水总量由东南向西北递减,再加上其水资源的利用率和利用效率低下,2013年全省水资源开发利用率仅为4.4%,这些都加剧了水资源的供需矛盾[2-3]。

青海省是农业大省,而水资源是粮食生产的基础,2013年青海省农业用水占总用水量的81.15%[2],因此掌握农业用水情况对青海省的持续发展起到了至关重要的作用。截至2013年,我国的农田灌溉水有效利用系数为0.52[4],而青海省的农田灌溉水利用系数为0.448[2],低于全国平均水平,水资源浪费情况十分严重,严重威胁了青海省的粮食安全和经济发展。因此有必要对青海省的农业用水进行预测,从而合理分配各行业的用水,加强农业用水效率,使得农田灌溉水有效利用系数达到0.55以上[5]。

目前,对于农业用水的分析主要集中在节水灌溉[3,6-7]以及对作物用水的测算[8-9]方面,而对农业用水的整体预测的研究相对较少[10-11],尤其是对多影响因子下的农业用水量预测。笔者筛选了11个影响青海省农业用水的因素,构建了偏最小二乘法模型,通过MATLAB软件进行模型的模拟运算。为了提高模型的精度并且简化模型,对偏最小二乘模型进行了改进,并将预测结果与实际观测结果进行对比检验。结果表明,所构建的模型有较高的准确性,是合理的。所构建模型在一定程度上为青海省预测农业用水提供了依据,并且对调节农业用水、提高农业用水效率提供了定量的标准,具有现实意义。

1　偏最小二乘回归模型

1.1偏最小二乘法的概念

偏最小二乘算法(partial least squares algorithm, PLSA)最早出现在20世纪70年代,Wold在研究经济学的过程中创建了非线性迭代偏最小二乘法[12]。偏最小二乘法同一般的回归方法相比,不仅具备了主成分分析、典型相关性分析和多元线性回归分析的优点[13],还能弥补这些方法的缺陷,解决自变量的多重共性问题,并且保证了主成分对因变量的解释力度,在解决实际问题时更具备优势。目前,PLSA在已被广泛运用于物理、生物、管理学等多领域,并在不断地改进中。

1.2PLSA的计算步骤

本文考虑单因变量的PLSA的回归模型,设有一个因变量y,p个自变量x1,x2,…,xp,样本数为n,将X和Y表示成矩阵Z=(X,Y),将原始数据进行标准化处理,记为E0和F0。按下列步骤建立回归方程:

1.2.1提取主成分

求矩阵ETFFTE最大特征值所对应的单位向量w1,由此得到自变量的第一主成分t1=E0w1,其中

(1)

(2)

然后求出E0对t1的回归方程及回归系数p1:

(3)

则回归方程的残差方程为:

(4)

令E1=E0,重复下面的步骤(2),直到满足精度要求,则成分提取完毕,现假设最终对自变量提取了k个主成分t1,t2,…,tk(k≤p)。

1.2.2确定成分提取的个数——交叉有效性

在偏最小二乘回归模型中,只需引入对模型精度有改进作用的成分,并且每引入一个成分都需要检验其是否提高模型预测的精度。

(5)

(6)

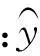
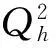
1.2.3变量投影重要性分析

在偏最小二乘回归建模中,用变量投影重要性指标I来说明自变量对因变量的解释能力,即自变量表达式为

(7)

式中:I指在解释因变量时,自变量的作用的重要性;r(y,th)是因变量y与提取的第h个主成分的相关系数;whj是第h个主成分对应的单位向量的第j个指标值。通常情况下,I越大,表明该变量对因变量的影响越大,该变量越重要。一般I≥1时,认为它为重要因素;I<0.5时,认为它为不重要因素。

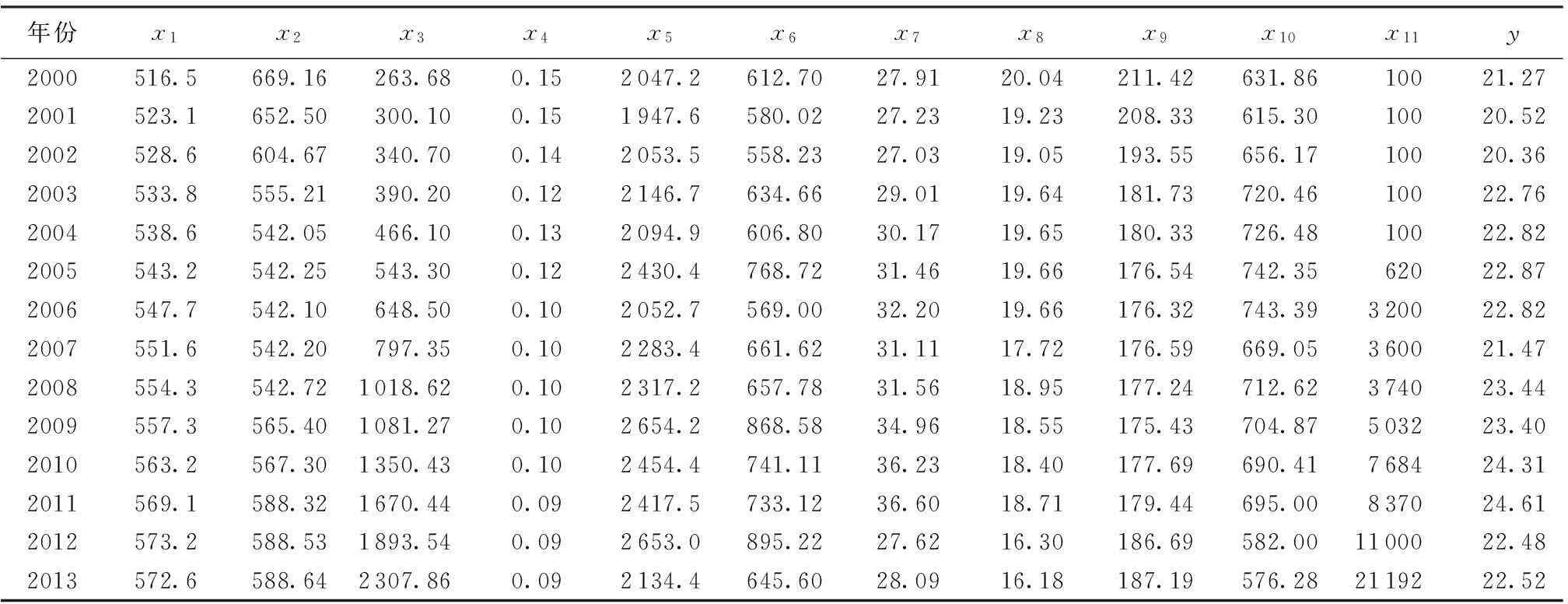
表1　青海省2000—2013年相关因子原始数据

1.2.4建立回归模型

按照以上步骤,确定可以提取k个主成分, 得到:

(8)

(9)

式中:p1,p2,…,pk为E0分别对t1,t2,…，tk,的回归系数;r1,r2,…,rk分别是因变量y与t1,t2,…,tk,相关系数;Fk为残值。

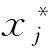
(10)

(11)

式中:E为单位矩阵。

1.3改进的PLSA

PLSA的目的是求解使方差V(ti)和相关系数C(ti,y)较大的成分,事实上,PLSA的结果是求解使协方差C(ti,y)较大的成分。这是由于在选择自变量时,无法剔除与因变量不相关的信息,因此要改进偏最小二乘回归模型,将解释性不强的变量剔除,使回归方程更加的简洁、准确。

本文在原有偏最小二乘回归模型的基础上采用后退法[14],对模型进行改进,具体步骤为:

a. 构建原始变量的偏最小二乘回归方程。

(12)

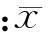
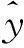
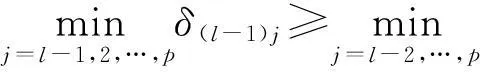
2　实证分析

本文根据青海省的实际状况,选取了11个影响农业用水(y,亿m3)的因子,分为社会经济系统因子:总人口(x1,万人)、耕地面积(x2,103hm2)、GDP(x3,亿元)、第一产业占GDP比例(x4,%);水资源系统因子:年降水总量(x5,亿m3)、水资源总量(x6,亿m3)、供水量(x7,亿m3)、农田灌溉用水量(x8,亿m3)、有效灌溉面积(x9,103hm2)、农田灌溉单位面积用水量(x10,m3);管理因子:水资源费征收(x11,万元),其中2000—2009年的数据作为训练样本,2010—2013年的数据作为检验样本(表1),统计的数据来自历年青海省统计年鉴、青海省水资源公报、中国水利年鉴和黄河年鉴。

2.1原始数据的偏最小二乘模型

表2　回归方程拟合值

表3　各轮变量剔除拟合误差值

注:表中打线段的单元格表示本轮次已删除变量。

2.2改进的偏最小二乘模型

由上述可知,原始数据的回归模型的精度较高,但解释变量较多,模型较为复杂,因此可以在提高精度的基础上,将一些解释性相对弱的变量剔除,由此得到更为简洁的回归模型。

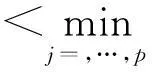
因此,在剔除了变量x10、x9、x11、x5、x1后所得的模型为最终模型,模型精度在原始模型的基础上提高了21.63%,回归方程为:y=0.444 7-0.006 7x2+0.002 1x3-8.790 7x4+0.001 8x5+0.073x6+1.145 5x7,各变量的系数与相关系数的符号一致,变量的剔除是有效的。

对检验样本进行检验,其拟合值如表4所示,从表4中可以得出,原始回归方程的平均拟合误差δ=4.610 1%,改进后的平均拟合误差δ=1.417 8%。从表4中可以直接看到,改进后的模型所得的每一个拟合值的拟合误差均小于原始模型的拟合误差, 进一步说明了改进后的偏最小二乘模型的预测精度更高,与观测值更贴近,因此对原始模型进行改进是必要的、有效的。

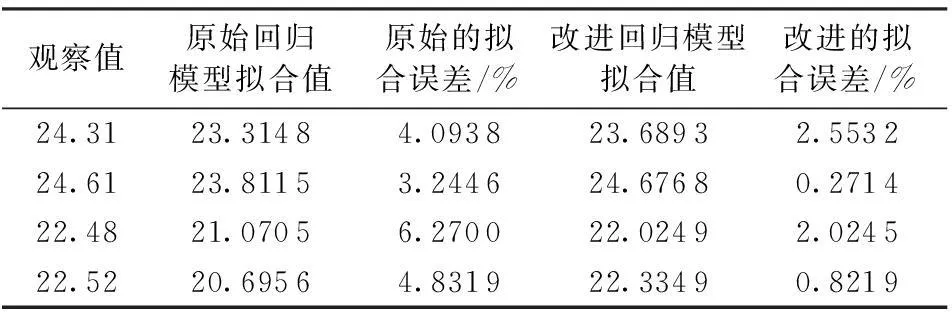
表4　检验样本拟合值

通过观察观测值、原始拟合值以及改进后的拟合值的贴近程度,如图1所示,发现两者与观测值都有较好的贴近度,但改进后的模型所得的拟合值与观测值的贴近度更高,因此更加证明了对模型进行改进的准确性,并且大大简化了模型,使模型运用起来更方便。通过建立模型来预测青海省的农业用水量,为合理分配各行用水提供了保障,并且通过分析不同解释变量对农业用水的影响的大小,为提高农业用水效率、减少浪费提供了依据。模型改进后,各变量对青海省农业用水的解释能力都较好(表5),其中农田灌溉用水量和供水量最为重要,农业用水中农田灌溉为主要耗水部分,并且青海省为农业大省,供的水越多,农业所分配的水量越多,因此这两个变量对农业用水量最为重要,符合实际情况,说明拟合模型与事实相符。此外,青海省水资源总量较为稳定,年际变化不大,对农业用水的影响相对于其他因素较小。其余因素对农业用水的重要程度较为接近,主要集中在社会经济因子中,影响程度接近1,说明经济的发展、社会的改变对农业用水有较大的影响。近年来,青海省政府不断引导社会向工业化发展,工业在国民生产中比重不断上升,青海省的产业结构在改变,农业的比例在减小,农业用水也会受到较大的影响,这与实际情况一致,进一步说明了模型的有效性。

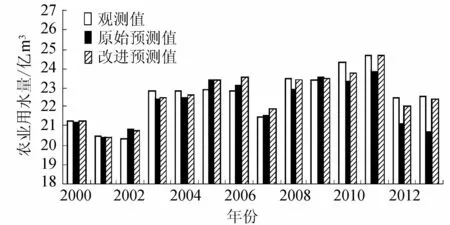
图1　模型拟合值

因数因数符号I农田灌溉用水量x81.2162供水量x71.0752耕地面积x20.9844GDPx30.9595第一产业占GDP比例x40.9535水资源总量x60.7522

3　结　论

a. 从社会经济系统、水资源系统和管理方面筛选11个影响青海省农业用水的解释变量,运用MATLAB软件对2000—2009年的数据建立偏最小二乘回归模型,得到平均拟合误差为1.255 9%,说明了PLSA的拟合精度较高。

b. 偏最小二乘模型无法剔除与因变量不相关的因子,通过改进模型,删减对农业用水量解释性不强的总人口、年降水总量、有效灌溉面积、农田亩均灌溉用水量、水资源费征收5个变量,得到拟合精度最高为0.9843%的回归模型,极大地简化了模型,并提高了模型精度。

c. 选取2010—2013年的数据为检验样本,在对检验样本进行检验后,得到较为贴近观测值的拟合值,表明模型的可靠性,并且改进后的模型的贴近度更高,说明了本文所得的预测模型与实际符合,具有现实意义。

参考文献：

[1] SUN Caizhi,ZHAO Liangshi,ZOU Wei,et al.Water resource utilization efficiency and spatial spillover effects in China[J].Journal of Geographical Sciences,2014,24(5):771-788.

[2] 青海省水利厅.2013年青海省水资源公报[EB/OL].[2015-05-03].http://www.qhsl.gov.cn/uploadfile/2013年 青海省水资源公报.pdf.

[3] 青海省统计局.青海省统计年鉴2014[M].北京:中国统计出版社,2014:24-30.

[4] 袁寿其,李红,王新坤.中国节水灌溉装备发展现状、问题、趋势与建议[J].排灌机械工程学报,2015,33(1):78-92.(YUAN Shouqi,LI Hong,WANG Xinkun.Status,problems,trends and suggestions for water-saving irrigation equipment in China[J].Journal of Drainage and Irrigation Machinery Engineering,2015,33(1):78-92.(in Chinese))

[5] 中华人民共和国中央人民政府.国家农业节水纲要(2012—2020)[EB/OL].[2015-05-03].http://www.gov.cn/zwgk/2012-12/15/content_2291002.htm.

[6] JENSEN M E.Beyond irrigation efficiency[J].Irrigation Science,2007,25(3): 233-245.

[7] 李保国,黄峰.1998—2007年中国农业用水分析[J].水科学进展,2010,21(4):575-583.(LI Baoguo,HUANG Feng.Trends in China’s agricultural water use during recent decade using the green and blue water approach[J].Advances in Water Science,2010,21(4):575-583.(in Chinese))

[8] ZHANG Yongqin,MIAO Qilong,PENG Buzhuo.Calculation and analysis on change of agricultural water consumption in the Changjiang delta[J].Journal of Geographical Sciences,2001,11(4):321-325.

[9] FU Yuanyuan,YANG Guijun,WANG Jihua,et al.Winter wheat biomass estimation based on spectral indices,band depth analysis and partial least squares regression using hyper spectral measurements[J].Computers and Electronics in Agriculture,2014,100(2):51-59.

[10] 田丝,张永丽.主成分回归模型在农业需水量预测中的应用[J].资源开发与市场,2012,38(7):580-582.(TIAN Si,ZHANG Yongli.Agricultural water demand forecast based on principal component regression model[J].Resource Development and Market,2012,38(7):580-582.(in Chinese))

[11] 刘迪,胡彩虹,吴泽宁.基于定额定量分析的农业用水需求预测研究[J].灌溉排水学报,2008,27(6):88-91.(LIU Di,HU Caihong,WU Zening.Predicting method for demand of agriculture water based on quantitative analysis[J].Journal of Irrigation and Drainage,2008,27(6):88-91.(in Chinese))

[12] 王惠文,吴载斌,孟洁.偏最小二乘回归的线性与非线性方法[M].北京:国防工业出版社,2006:56.

[13] 王琛娇.低碳视角下的城市交通发展路径研究[D].无锡:江南大学,2012.

[14] 杨国栋.基于变量筛选的偏最小二乘回归方法及其应用[D].长沙:中南大学,2013.

DOI：10.3880/j.issn.1004-6933.2016.04.009

作者简介:王洁(1990—),女,硕士研究生,研究方向为管理科学与工程。E-mail:1174764572@qq.com 通信作者:章恒全,教授,博士。 E-mail:hqzhang630@163.com

中图分类号：TV211.1

文献标志码：A

文章编号：1004-6933(2016)04-0055-05

(收稿日期：2015-09-08编辑：徐娟)

Application of improved partial least squares method to prediction of agricultural water consumption in Qinghai Province

WANG Jie, ZHANG Hengquan

(Business School, Hohai University, Nanjing 211100, China)

Abstract：Based on the basic data of 11 factors that influenced the agricultural water consumption of Qinghai Province from 2000 to 2009, a partial least squares regression model was established. Considering the practicality and accuracy of the model, the backward method was used to improve the partial least squares method. Five unnecessary variables were excluded, and a higher prediction accuracy was obtained. Data from 2010 to 2013 were selected to verify the model. The results show that the prediction using the partial least squares method agreed with the actual situation, and the improved model showed even greater agreement. Therefore, the partial least squares method is highly applicable to the prediction of the agricultural water consumption of Qinghai Province. The improved partial least squares method greatly simplifies the original model, improves the prediction accuracy, and provides a basis for the prediction of the agricultural water consumption of Qinghai Province.

Key words：agricultural water consumption; water consumption prediction; improved partial least squares method; Qinghai Province