基于两阶段搜索算法的多峰函数优化
2016-08-12李焕哲吴志健郭肇禄刘会超汪慎文
李焕哲,吴志健,郭肇禄,刘会超,汪慎文
(1.武汉大学计算机学院软件工程国家重点实验室,湖北武汉 430072; 2.河北地质大学信息工程学院,河北石家庄 050031;3.江西理工大学理学院,江西赣州 341000)
基于两阶段搜索算法的多峰函数优化
李焕哲1,2,吴志健1,郭肇禄3,刘会超1,汪慎文2
(1.武汉大学计算机学院软件工程国家重点实验室,湖北武汉 430072; 2.河北地质大学信息工程学院,河北石家庄 050031;3.江西理工大学理学院,江西赣州 341000)
多峰优化问题需要搜索多个最优值(全局最优/局部最优),这给传统的优化算法带来很大程度上的挑战.本文提出了一种两阶段算法求解多峰优化问题.第一阶段采用带有邻域变异策略的排挤差分演化算法进行粗粒度搜索,在适应度景观上尽可能多的找到最优解的大概位置.搜索一定代数之后,调用DMC聚类方法把搜索种群划分成多个聚类,然后在每个聚类上调用协方差矩阵自适应演化策略算法进行精细搜索.另外,本文还提出搜索点补充策略用于平衡每个聚类的大小及增加算法初期的搜索能力.我们提出的方法和9个较新的经典算法在两个基准测试集上进行了大量对比测试,结果表明新算法是有效的,在大多数测试函数上都优于其它算法.
排挤差分演化;协方差矩阵自适应演化策略;多峰优化;小生境;邻域变异
1 引言
在实际工程实践中,有一类问题需要同时搜索多个最优解,这类问题通常被称为多峰优化问题.例如模式匹配与识别、神经元的结构及权重优化、模糊系统结构和参数优化等,都是多峰优化的应用场景.但是,传统的演化算法[1,2]最初被设计用于搜索单一的全局最优解,由于全局选择方案的使用使得种群一般会收敛到单一最优解.因此,传统的演化算法并不适用于直接求解多峰优化问题.为了解决这个问题,人们经常把传统的演化算法与某种技术(例如重启技术、多种群技术、小生境技术、双目标技术)相结合来求解多峰优化问题.在众多的技术中,小生境(Niching)技术[3,4]是使用最为广泛的技术之一.近几十年中,在演化计算领域较为流行的小生境技术主要包括排挤技术、清除技术、适应度共享技术、物种生成技术、聚类技术和受限的锦标赛选择技术.
排挤技术(Crowding)由De Jong在1975年提出,用于求解多峰优化问题.2004年,Thomsen把排挤技术引入差分演化算法,称之为CDE(Crowding Differential Evolution),来求解多峰优化问题.2012年,Qu等[5]把邻域变异策略引入CDE,提出了NCDE算法.在NCDE(Neighborhood-based CDE)算法中,实验向量的生成被限制在一定数量的相似个体(以欧氏距离度量相似性)之间,通过这种方法,每个个体都向离它最近的更好个体演化并且降低了在不同小生境之间生成实验向量的概率,这有助于更好的保持种群的多样性.NCDE算法有两个主要优点:其一,它具有很强的全局搜索能力以及良好的保持种群多样性的能力.其二,NCDE是一种隐式小生境技术,在保持种群多样性上对种群的大小要求不高,在极端情况下,甚至每个个体都可以独立保持一个小生境.但是,NCDE这种低选择压力机制无疑会降低它的收敛速度.此外,为了提高局部搜索能力,交叉概率CR通常会被设置为一个较小的值,例如0.1,这有可能降低其在不可分问题上的性能.
Hansen等在1996年首先把协方差矩阵自适应(Covariance Matrix Adaptation,CMA)方法引入演化策略(Evolution Strategy,ES),以达到对搜索空间的任意可逆线性变换具有不变性和让搜索分布形状适应问题的实际适应度景观的目的.CMA-ES[7]算法克服了一些传统演化算法相关的典型问题,例如在严重缩放和高度不可分问题上的低性能、对大种群的内在需求以及种群的早熟问题.然而,在其本质上,CMA-ES算法是一种局部搜索算法,它具有很强的局部搜索能力,但在全局搜索能力上相对较弱[8].
基于以上的分析,为了弥补NCDE收敛速度慢及CMA-ES全局搜索能力弱的缺点,我们提出了一种基于NCDE和CMA-ES的两阶段杂交算法.在第一阶段充分发挥NCDE算法全局搜索能力强的特点进行粗粒度搜索,尽可能多的定位最优解的大概位置.在NCDE演化一定代数之后,调用DMC聚类方法识别当前种群中形成的聚类.然后,根据识别出的聚类数量,相同数量的CMA-ES实例被生成,每一个CMA-ES实例对应一个不同的聚类.每个聚类的最好搜索点作为CMA-ES的起始搜索点,每个聚类与其最近相邻聚类欧氏距离的六分之一作为CMA-ES的起始搜索步长,每个实例被独立的运行直到终止条件满足.为了充分地利用剩余的函数评价次数,算法采用了CMA-ES实例重新初始化和档案存储机制.
2 相关工作介绍
因为本文提出的算法将要用到检测多峰算法、NBC聚类、DMC聚类和CMA-ES算法,为了便于阐述提出的算法,下面简要介绍一下关于这几种算法的相关工作.
2.1检测多峰算法
检测多峰算法(Detect Multimodal,DM)[9]用于检测搜索空间中的两个点是否跟踪同一个最优值,即验证这两个点之间是否存在一个山谷.如果有一个山谷存在,这意味着它们没有跟踪同一个最优值.假设求解最大化问题,为了检测两个点之间是否存在山谷,需要生成一些内部插值点并均匀地插入两个测试点之间.如果所有插值点的函数值都高于两个测试点的最小函数值,则可认为这两个测试点跟踪同一个最优值.DM方法消耗评价次数,为了减少评价次数的消耗,插值点个数不适于设置过大的值,大多数情况下取值在2到10之间即可.
2.2NBC聚类
NBC(Nearest-Better Clustering)聚类方法由Preuss[8]提出,它被认为是一个无参数的聚类方法.NBC方法通过连接每一个个体到离它最近且更好的邻近个体来构造一个生成树(如果存在多个全局最优值,则构造成树林),然后根据一系列规则修剪树(移除个体之间的边),最后修剪完成后的结果即为最终的聚类结果.第一个修剪规则是删除那些比φ×μdist长的边,μdist代表所有边的平均长度,φ是一个权重系数,通常被设置为2.然而这个规则在高维问题中是不可靠的,通常会低估吸引盆的个数.为了克服这个问题,Preuss接着又提出了第二个修剪规则.当一个个体具有3个或更多内向边时,如果它的外向边长度大于β×μdist,则移除这个外向边.μdist代表该个体所有内向边的中位数,β为权重系数.假定求解最大化问题,nearest-better距离可被定义为dnb(xi,P)=min{dist(xi,xj)|f(xj)>f(xi)∧∀xj∈P},f(·)代表评价函数.
2.3DMC聚类
DMC(Detect-Multimodal Clustering)聚类方法由Stoean[9]提出,该方法采用检测多峰算法进行聚类识别.这种聚类方法不依赖于小生境半径或个体的索引值,它依赖于适应度景观上的种群拓扑结构来划分聚类,是一种基于种群拓扑结构的聚类方法.这一特性使得该方法的聚类结果可以是不规则形状的.与NBC聚类方法相比,DMC方法需要指定内部插值点的个数(参数IP),并且消耗额外的评价次数才能识别聚类.但是,如果设置一个合理的IP值,DMC方法能够取得比NBC方法更准确的聚类划分结果.
2.4CMA-ES算法
CMA-ES是一种可用于求解非线性和非凸问题,无需求导的随机局部搜索算法.它采用基于统计的方法更新协方差矩阵和变异步长,以达到去随机化的目的.基于协方差矩阵自适应的学习机制使其对搜索空间的任意可逆线性变换具有不变性,对于病态的、高度不可分的问题有优秀的求解能力.CMA-ES有多种变体,最常见是(μw,λ)-CMA-ES,表示从λ个子个体中选择最好的μ个个体作为父个体生成下一代的加权均值向量m.新的搜索点通过随机抽取一个多元正态分布来产生变异,其公式如下:
(1)
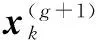
3 提出的算法
本节我们提出基于NCDE和CMA-ES的两阶段算法,在第一阶段中分别采用NBC聚类和DMC聚类方法进行聚类识别,以分析这两种聚类方法的性能.分别称这两种新算法为NBC-CMA和DMC-CMA.
3.1NBC和DMC聚类性能比较
下面比较NBC和DMC在不考虑评价次数消耗的情况下,它们之间聚类性能的差异.参数IP(插入点数量)设置为10,两种聚类方法在测试集1中的6个函数上进行对比实验.实验考察两种聚类算法随演化代数的增加,它们聚类性能上的变化.在NCDE算法运行过程中,每隔一定代数记录聚类算法识别的聚类数目,对每个函数两种方法分别独立运行50次,以平均找到的聚类数目作为比较对象,实验结果如图1所示.

曲线上的数字代表该函数所对应的种群大小,在函数F6(2D,3D)、F7(2D)和F12(5D)上,DMC表现出了更优秀和稳定的聚类性能.尽管在F7(2D)上NBC取得了更多的聚类数量,但是DMC的结果更接近F7(2D)函数真实的最优值数量.在F12函数上,可以看到DMC识别的聚类数目多于NBC,并且它们的聚类性能在迭代初期都非常差,NBC的聚类性能接近于1.但随着演化代数的增加,它们的聚类性能逐渐增强.在没有考虑评价次数的情况下,DMC的性能似乎优于NBC算法.但是,在大种群的情况下DMC算法会消耗大量的评价次数,因此在这种情况下DMC算法并不适于被频繁使用.另外,从下面子图1(c)中的函数F6可以看到,NCDE算法有优秀的保持种群多样性的能力,由DMC识别出的平均聚类数量几乎接近于对应的种群数量,这意味着种群中的每个个体几乎独立维护着一个不同的吸引盆.这是我们选择NCDE算法作为第一阶段算法的一个原因.
3.2搜索点补充策略
算法1SPRS策略
输入:MINindi,C,R
1.从聚类集合C中分别选择包含最多和最少搜索点数量的聚类cmax和cmin
2.如果cmin中的搜索点数目大于等于MINindi,则算法终止
3.从聚类cmax中选择一对具有最大相似性(以欧氏距离度量)的搜索点
4.从被选择的一对搜索点中选择适应度较低的搜索点pk,并把它加入到cmin中
5.根据公式(2)计算重新初始化半径rreinit
6.在半径rreinit内均匀随机地初始化搜索点pk
7.跳转到step1
为了在演化初期增强搜索新峰的能力、平衡子种群的大小以及保持子种群的稳定性,本节提出了搜索点补充策略(Search Point Replenishment Strategy,SPRS).它的主要思想是在演化初期增加小生境间搜索点的迁移,通过搜索点迁移来达到增大搜索空间和平衡子种群的目的.对SPRS的使用有以下几点需要注意:(1)SPRS仅在算法的运行初期有效,因为只有较大的初始化半径才可扩大搜索空间以增加发现新最优值的概率.相反,在算法后期,由于初始化半径的收缩,调用SPRS已不能起到扩大搜索空间的目的,对SPRS的调用变得没有必要.(2)没有必要每次迭代都调用SPRS,为了节省计算开销,可以以指数递增方式调用SPRS.其伪代码如算法1所示.
其中,MINindi是聚类中允许的最少搜索点数量,它可由种群数量除以聚类数目CN求得.聚类集合C和聚类数量CN由NBC或DMC方法获得.R用于计算重新初始化半径rreinit.
(2)
dn(cmin,C)计算cmin到离它最近的聚类之间的距离(两个聚类中最好搜索点之间的距离),cmin代表包含最少搜索点的聚类.R为收缩因子用于限制重新初始化半径的大小,如果演化代数小于4,R=1,否则R=iter-3,iter为当前演化代数.这样做的目的是保证在算法运行早期有更大的初始化半径,随着演化代数的增加,初始化半径逐渐缩小.

图2给出NBC-CMA算法在F7-2D函数上第32次迭代后,调用SPRS和不调用SPRS的种群快照结果.图2(a)在搜索新的最优值上明显优于图2(b),而且图2(a)上每个聚类的个体数量更均衡,这有利于保持聚类的稳定性.
3.3提出的算法框架
在算法的迭代过程中,算法分两个阶段执行,在第一阶段执行NCDE算法进行粗粒度搜索,当满足一定条件时SPRS会被调用.首先,当前聚类数量要大于问题维度D;其次,只有当前迭代次数等于阈值α时.这样做可以使得对SPRS的调用随演化的进行逐渐减少.第三,为了进一步限制对SPRS的调用,如果当前消耗的评价次数大于等于总评价次数的五分之一时,则不再调用SPRS.
α=(max(2,log2(D)))t,t=2,…,n
(3)
下面要解决何时转入第二阶段的问题,我们引入了一个自适应的启发式参数θ,当已消耗的评价次数大于等于阈值θ时,终止第一阶段并转入第二阶段的准备阶段.公式中的MaxFEs代表允许的最大评价次数.
θ=MaxFEs/max(2,5-log2(D))
(4)
在第二阶段开始前的准备阶段,需要精确的对种群划分聚类,所以此时调用DMC方法进行聚类划分,以期望获得更准确的划分结果.然后和已获得聚类数目相同的(μw,λ)-CMA-ES实例被生成,每一个CMA-ES实例对应一个聚类并覆盖搜索空间中的一个不同区域.取聚类中的最好搜索点作为CMA-ES实例的起始搜索点,并定义当前实例与它最邻近实例之间欧氏距离的二分之一为覆盖距离,则取覆盖距离的三分之一作为当前实例的起始步长,这样做的目的在于希望在CMA-ES随机抽取的搜索点中,有99%的搜索点落在覆盖距离之内.这样可以从统计上避免邻近CMA-ES实例间覆盖范围的相互重叠.为了充分利用剩余的评价次数,引入了CMA-ES实例重新初始化和档案存储机制,当一个实例被终止并且有剩余的评价次数时,该实例被会重新随机初始化并重新启动它.算法框架的伪代码如算法2所示.
算法2算法框架
1.初始化种群
2.执行聚类方法识别聚类
3.如果CN>D,则执行SPRS,否则跳过该步
4.converged=false,iter=0,t=2
5.while终止条件没有满足do
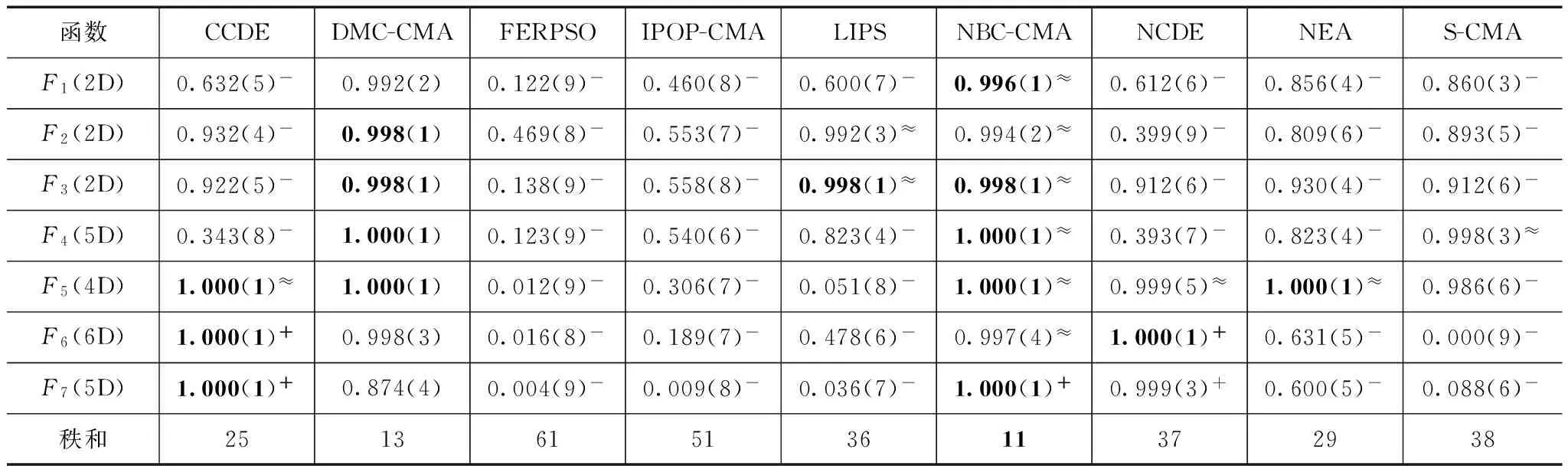
(a)if not converged then
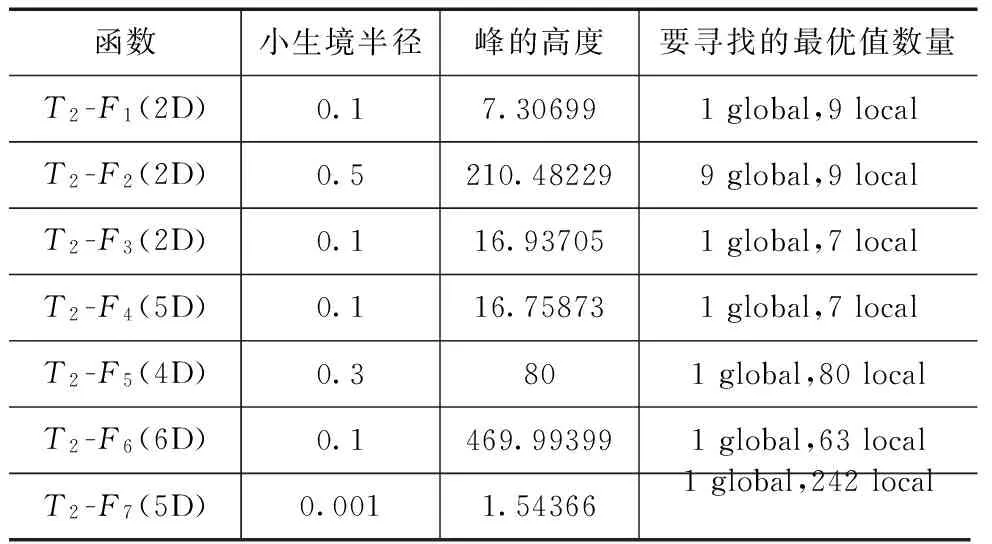
①如果CN>D∩iter=α∩FEs ②执行NCDE算法 ③如果FEs>=θ,则执行DMC划分聚类并初始化CMA-ES实例,并令converged=true (b)else ①分别执行所有CMA-ES实例 ②若条件满足执行档案存储和实例重启 (c)iter=iter+1 6.end while FEs代表目前消耗的评价次数,CN为NBC或DMC聚类算法返回的聚类数目. 3.4时间复杂度分析 本文提出算法的复杂性与NCDE、CMA-ES、NBC、DMC和SPRS等算法复杂性有关.NCDE和NBC的复杂性为O(n2log(n)),n为种群大小.CMA-ES的复杂性为O(n3),n为问题的维度.而DMC聚类方法的复杂性难于确定,因为它与函数评价有关.在不考虑函数评价的情况下,DMC的复杂性小于等于NBC的复杂性,相等只出现在找到的最大聚类数量等于种群数量时.在评价函数不是特别复杂的情况下,由于本文提出的算法框架对DMC和NBC聚类方法仅调用几次,并且它们的复杂度并不占主导因素,可以把它们忽略.对于SPRS方法,它的复杂性在O(1)到O(n3)之间,其中n为种群大小.在大多数情况下,由于SPRS仅被调用几次,SPRS的运行时间是可以忽略的,但在种群中仅包含少数几个聚类,且聚类中的个体数量极不均匀的情况下,SPRS对算法运行时间有一定影响.根据上面的分析,本文提出算法的复杂性主要取决于NCDE和CMA-ES算法的复杂性.NCDE算法的复杂性依赖于种群的大小,而CMA-ES算法的复杂性依赖于问题维度的大小.一般来说,在低维问题上NCDE算法的复杂性占主导因素(因为种群大小远大于问题维度),而在高维问题上CMA-ES算法的复杂性占主导因素(即当O(Nn3)>O((NP)2log(NP))时,N为小生境数量,n为问题维度,NP为种群大小).因此,在低维问题上本文提出的算法的运行时间少于原始NCDE算法,而在高维问题上我们提出的算法的运行时间可能会大于NCDE算法,这取决于种群大小和问题的维度. 4.1测试函数 为了评估提出算法的性能,本文使用了两个基准测试集.以CEC2013会议竞赛设计的20个多峰基准测试函数为测试集1,用以检验算法搜索全部全局最优解的能力.另外,又选择了其它7个常用测试函数作为测试集2,用以检验算法同时搜索全部全局最优解及部分局部最优解的能力.有关测试集1的详细介绍请参考文献[10].测试集2共包含7个测试函数,它们是: F1:Waves (2D) F2:Shubert (2D) F3:Modified Shekel (2D) F4:Modified Shekel (5D) F5:Rastrigin (4D) F6:Szu (6D) F7:Ackley (5D) 所有这些函数均为最大化问题.F1和F2选自文献[9].F3到F7选自文献[11]. 4.2性能评价 本文使用文献[10]中所规定的性能评价方法对算法进行定量评价.这些评价方法需要在给定的精度要求下,运行被测算法多次,然后通过对多次运行结果进行计算得到评价指标. 峰比率(Peak Ratio,PR)按式(5)计算,NPFi代表算法第i次运行结束后找到的最优值数量,NKP是已知最优值数量,PR度量在NR次运行中找到已知最优值数量的平均百分比. (5) 4.3实验设置 本实验中所有算法代码均由Visual C++2012编写,操作系统为Window7,CPU为Intel 酷睿i7-4790k.为了检验NBC-CMA和DMC-CMA算法的性能,我们选择了9个对等的算法进行比较.它们是NEA[8]、TN-CMA-ES[12]、S-CMA[13]、IPOP-CMA-ES[14]、CCDE[15]、NCDE[5]、LIPS[16]、FERPSO[17]和PNA-NSGA-II[18].其中IPOP-CMA-ES是基于重启机制、时间上串行运行的算法,原则上空间上并行化的算法性能应不次于它,这里以它作为一个测试基准,来检验所有算法的性能. 除了TN-CMA-ES和PNA-NSGA-II(它们的实验结果引自相应参考文献)算法以外,剩余所有算法都在5种精度e={1.0e-1,1.0e-2,1.0e-3,1.0e-4,1.0e-5}中的每一种精度下独立运行50次.最大允许的评价次数根据问题选择: 5.0e+04用于T1-F1到T1-F5(1D or 2D) 2.0e+05用于T1-F6到T1-F11(2D) 4.0e+05用于T1-F6到T1-F12(≥3D) 3.0e+04用于T2-F1到T2-F4(2D or 5D) 1.0e+05用于T2-F5到T2-F6(4D or 6D) 2.0e+05用于T2-F7(5D) 测试基准为每个函数提供了指定的参数,其中部分参数作为被执行算法的输入使用,测试集1的参数见文献[10],测试集2的参数见表1.一般来说,种群的大小对大多数算法的性能都有影响,为了保证比较的公平性,所有算法都在不同种群大小下(以步长50递增)被执行多次.对于每一个种群大小,所有算法都被独立执行50次并计算其PR值及平均找到的最优值个数,然后从所有运行结果中选择最好运行结果作为最终结果参与比较. 我们提出的算法共引入了3个新参数IP,α和θ,DMC-CMA和NBC-CMA的参数IP分别被设置为固定值6和8.α和θ是两个自适应参数,不需要设置.对于NEA和S-CMA算法,它们的最大允许小生境数量设置为要搜索的最优值数量.为了保证和其它CMA算法比较的公平性,在原IPOP-CMA-ES和S-CMA算法的基础上为其增加了档案存储机制.其它算法的参数均取其默认值. 表1 测试集2性能评价所需的参数 在两个测试集27个函数上,求解精度为1.0e-5时,所有算法对每个种群大小都独立运行50次.图3展示了在最好种群下部分函数的实验情况.对全部测试函数选择最好种群下的实验结果分别列在表2和表3中.对每个函数最好实验结果以粗体显示,每种算法的秩显示在小括号中,算法的秩和列在表格的最后一行.为了确定DMC-CMA算法的优势相对于其它算法在统计上的显著性,从实验结果中选择所有算法的最好实验结果,对50次运行中所有求得的50组最优值个数,在DMC-CMA和其它算法之间以0.05为显著性水平执行Wilcoxon秩和检验.若两组算法性能存在显著性差异,则比较它们的平均找到的最优值个数.“-”、“+”和“≈”分别代表相应算法的性能劣于、优于和近似于DMC-CMA算法.最终秩和检验的结果列于表2和表3中. 从表2和表3可以看到,DMC-CMA和NBC-CMA有近似的性能,DMC-CMA的性能略优于NBC-CMA,二者仅在个别函数上有所区别.DMC-CMA和NBC-CMA的性能明显优于其它算法,这说明我们提出的方法是有效的,具有更好的适应性.根据表2和表3的秩和可以看到,DMC-CMA和NBC-CMA性能最好,NEA和S-CMA次之.从整体上看,IPOP-CMA-ES在一定程度上受随机性的影响,因为它每次重启运行的初始搜索点是随机从搜索空间中选取.因此,对于一些包含大量最优值的函数,IPOP-CMA-ES仅通过多次重启很难获得全部最优值.例如在T1-F6(2D,3D)、T1-F7(2D,3D)和测试集2上.然而在复合函数上,IPOP-CMA-ES的性能是可接受的,这证明了CMA-ES算法在病态和高度不可分的复杂问题上的优秀能力.FERPSO和PNA-NSGA-II算法在低维问题上性能较好,但在高维问题上它们的性能明显劣于其它算法.另外,FERPSO在搜索局部最优值上表现最差,这是因为该算法使得每个粒子向离它最近且适应度最好的邻近个体移动,这使得粒子更多的向全局最优值移动,容易丢失局部最优.CCDE、LIPS和NCDE算法有近似的性能,它们都采用了基于邻域变异的策略,都有很好的保持种群多样性的能力,具有很好的算法稳定性和一致性.NEA、S-CMA、TN-CMA-ES都采用了CMA-ES算法和相应的聚类识别技术进行最优值搜索,多数函数上它们有近似的性能,在总体上NEA和S-CMA的性能优于TN-CMA-ES.在复合函数上它们都有不错的表现,近一步证明了CMA-ES算法有较强的局部搜索能力及解决复杂问题的能力.在测试集2上,NEA算法整体上优于S-CMA算法,表现了出了更强的局部搜索能力.虽然DMC-CMA和NBC-CMA有近似的性能,但在某些函数上它们有着不同的性能.DMC-CAM在T1-F7(3D)、T1-F12(10D)函数上明显优于NBC-CMA算法,而NBC-CMA在T2-F7(5D)函数上优势明显. 5.1求解精度的影响 为了检验算法在不同求解精度下的性能差异,所有算法在最好种群规模下,对5种求解精度(1.0e-1到1.0e-5)中的每一种精度独立运行50次.两个测试集中的部分函数的实验结果绘制在图4中.结果表明DMC-CMA、NBC-CMA和IPOP-CMA-ES是最少受到求解精度影响.我们提出的算法因为采用了两阶段搜索,这一策略能够增加搜索的准确性,减少搜索的随机性,同时在已找到的吸引盆上利用CMA-ES进行局部精确搜索能够增加收敛速度,减少评价次数的消耗.算法的这些特性能够减少受求解精度改变的影响. 5.2收敛速度比较 为了比较所有算法的收敛速度,在求解精度1.0e-5下,所有算法在最好种群下独立执行50次,每次运行时记录每次迭代后找到的最优值数量.为了便于统计,让FEs以一定间隔递增,把每次迭代后找到的最优值数量记录于当前FEs下,然后计算所有算法50次运行后在不同FEs下的PR值.从两个测试集中选择11个函数进行实验,部分实验结果绘制在图5中.从图5可以看到DMC-CMA和NBC-CMA算法在运行初期收敛速度较慢,这是因为NCDE方法本身就是一个收敛速度慢的算法,在调用SPRS后可能会毁坏已收敛的种群结构,导致进一步降低收敛速度.但是当算法转入第二阶段后,算法的性能有一个明显的提升.这是因为在第二阶段中使用多个CMA-ES实例在前面已找到的吸引盆上进行精细搜索.搜索的准确性及CMA-ES算法的快速收敛特点使得我们提出的算法在第二阶段具有良好的收敛速度.与原始的NCDE算法相比,DMC-CMA和NBC-CMA在函数T2-F5(4D)、T2-F6(6D)和T2-F7(5D)上收敛速度更慢,但在其它函数上,DMC-CMA和NBC-CMA的收敛速度明显好于原始的NCDE算法.在函数T1-F6(2D)、T1-F6(3D)、T2-F5(4D)、T2-F6(6D)和T2-F7(5D)上,CCDE算法表现出了优于DMC-CMA和NBC-CMA的收敛速度. 表2 测试集1最好结果的PR值,求解精度为1.0e-5 表3 测试集2最好结果的PR值,求解精度为1.0e-5 函数CCDEDMC-CMAFERPSOIPOP-CMALIPSNBC-CMANCDENEAS-CMAF1(2D)0.632(5)-0.992(2)0.122(9)-0.460(8)-0.600(7)-0.996(1)≈0.612(6)-0.856(4)-0.860(3)-F2(2D)0.932(4)-0.998(1)0.469(8)-0.553(7)-0.992(3)≈0.994(2)≈0.399(9)-0.809(6)-0.893(5)-F3(2D)0.922(5)-0.998(1)0.138(9)-0.558(8)-0.998(1)≈0.998(1)≈0.912(6)-0.930(4)-0.912(6)-F4(5D)0.343(8)-1.000(1)0.123(9)-0.540(6)-0.823(4)-1.000(1)≈0.393(7)-0.823(4)-0.998(3)≈F5(4D)1.000(1)≈1.000(1)0.012(9)-0.306(7)-0.051(8)-1.000(1)≈0.999(5)≈1.000(1)≈0.986(6)-F6(6D)1.000(1)+0.998(3)0.016(8)-0.189(7)-0.478(6)-0.997(4)≈1.000(1)+0.631(5)-0.000(9)-F7(5D)1.000(1)+0.874(4)0.004(9)-0.009(8)-0.036(7)-1.000(1)+0.999(3)+0.600(5)-0.088(6)-秩和251361513611372938 本文提出了一个基于NCDE和CMA-ES算法的两阶段杂交算法求解实值多峰优化问题.提出的算法充分利用了它们的两个明显特点,即NCDE具有较强的保持种群多样性的能力和CMA-ES具有优秀的局部搜索能力.NCDE为了保持种群的多样性,降低了收敛速度,而第二阶段的CMA-ES所具有的快速收敛能力恰好弥补了这一劣势,既保证了种群的多样性,又保证了快速收敛.为了在第一阶段搜索后准确定位当前种群搜索到的最优值位置,我们引入了DMC聚类方法来划分聚类,该聚类方法虽然消耗了一定数量的评价次数,但可以获得更准确的聚类结果.为了增强种群在演化初期的搜索能力及保持种群的稳定性,我们引入了搜索点补充策略.该策略在一些低维函数上取得到明显优势,尤其在T1-F7(2D)、T1-F7(3D)、T2-F1(2D)和T2-F7(5D)函数上.大量的实验表明我们提出的算法在大多数测试函数上优于其它算法,表现出了优秀的性能和适应性.在两个测试集上的实验同时也表明我们提出的算法不仅在搜索全局最优值上有优良的性能,而且在搜索局部最优值上也性能优异. 下一步的工作将继续完善算法框架,与更多的多峰算法在更广泛的基准测试函数上进行比较研究.另外,将提出的算法尝试应用到动态环境下的多峰优化问题. [1]周新宇,吴志健,等.一种精英反向学习的粒子群优化算法[J].电子学报,2013,41(8):1647-1652. Zhou Xin-yu,Wu Zhi-jian,et al.Elite opposition-based particle swarm optimization[J].Acta Electronica Sinica,2013,41(8):1647-1652.(in Chinese) [2]彭虎,吴志健,等.基于精英区域学习的动态差分进化算法[J].电子学报,2014,42(8):1522-1530. Peng Hu,Wu Zhi-jian,et al.Dynamic differential evolution algorithm based on elite local learning[J].Acta Electronica Sinica,2014,42(8):1522-1530.(in Chinese) [3]李康顺,韦蕴珊,等.小生境演化算法下的WDCT图像压缩方法[J].电子学报,2014,(4):809-814. Li Kang-shun,Wei Yun-shan,et al.WDCT image compre-ssion based on niching evolutionary algorithm[J].Acta Electronica Sinica,2014,42(4):809-814.(in Chinese) [4]郑金华,刘磊,等.一种自适应小生境分布性保持策略[J].电子学报,2012,40(11):2330-2335. Zheng Jin-hua,Liu Lei,et al.An adaptive niche for keeping the diversity of solutions in multi-objective evolutionary algorithm[J].Acta Electronica Sinica,2012,40(11):2330-2335.(in Chinese) [5]Qu B Y,Suganthan P N,Liang J J.Differential evolution with neighborhood mutation for multimodal optimization[J].IEEE Transactions on Evolutionary Computation,2012,16(5):601-614. [6]Hansen N,Ostermeier A.Completely derandomized self-adaptation in evolution strategies[J].Evolutionary Computation,2001,9(2):159-195. [7]Hansen N.The CMA Evolution Strategy:A Comparing Review[M].Berlin:Springer,2006.75-102. [8]Preuss M.Niching the CMA-ES via nearest-better clustering[A].Proceedings of the 12th Annual Conference Companion On Genetic and Evolutionary Computation[C].Portland:ACM,2010.1711-1718. [9]Stoean C,Preuss M,Stoean R,et al.Multimodal optimization by means of a topological species conservation algorithm[J].IEEE Transactions on Evolutionary Computation,2010,14(6):842-864. [10]Li X D,et al.Benchmark Functions for CEC′2013 Special Session and Competition on Niching Methods for Multim-odal Function Optimization[R].Melbourne:RMIT University,Evolutionary Computation and Machine Learning Group,2013.1-10. [11]Vitela J E,Castaos O.A sequential niching memetic algorithm for continuous multimodal function optimization[J].Applied Mathematics and Computation,2012,218(17):8242-8259. [12]Pereira M W,et al.A topological niching covariance matrix adaptation for multimodal optimization[A].Proc of IEEE Congress on Evolutionary Computation[C].Betjing:IEEE,2014.2562-2569. [13]Shir O M,Emmerich M,Back T.Adaptive niche radii and niche shapes approaches for niching with the CMA-ES[J].Evolutionary Computation,2010,18(1):97-126. [14]Auger A,Hansen N.A restart CMA evolution strategy with increasing population size[A].Proc of IEEE Congress on Evolutionary Computation[C].Edinburgh,Scotland:IEEE,2005.1769-1776. [15]Gao W,Yen G G,Liu S.A cluster-based differential evolution with self-adaptive strategy for multimodal optimization[J].IEEE Transactions on Cybernetics,2014,44(8):1314-1327. [16]Qu B Y,Suganthan P N.A distance-based locally informed particle swarm model for multimodal optimization[J].IEEE Transactions on Evolutionary Computation,2013,17(3):387-402. [17]Li X D.A Multimodal particle swarm optimizer based on fitness euclidean-distance ratio[A].Proc of The 9th Annual Conference on Genetic and Evolutionary Computation[C].London:ACM,2007.78-85. [18]Bandaru S,Deb K.A parameterless-niching-assisted bi-objective approach to multimodal optimization[A].Proc of IEEE Congress on Evolutionary Computation[C].Cancun:IEEE,2013.95-102. 李焕哲男,1975年生,河北唐山人,武汉大学计算机学院博士研究生,研究方向:智能计算、机器学习. E-mail:lihuanzhe@whu.edu.cn 吴志健男,1963年生,教授,博士生导师,武汉大学软件工程国家重点实验室副主任,研究方向:智能计算、 并行计算和智能信息处理. E-mail:zhijianwu@whu.edu.cn 郭肇禄男,1984年生,江西南康人,博士,研究方向为智能计算、并行计算和机器学习. E-mail:gzl@whu.edu.cn 刘会超男,1982年生,河南驻马店人,博士生,研究方向为智能计算. E-mail:huichaoliu@whu.edu.cn 汪慎文男,1979年生,副教授,博士后,研究方向为智能计算与机器学习等. E-mail:wangshenwen@whu.edu.cn Multimodal Function Optimization Based on Two-Stage Search Algorithm LI Huan-zhe1,2,WU Zhi-jian1,GUO Zhao-lu3,LIU Hui-chao1,WANG Shen-wen2 (1.StateKeyLabofSoftwareEngineering,ComputerSchool,WuhanUniversity,Wuhan,Hubei430072,China;2.SchoolofInformationEngineering,HebeiGEOUniversity,Shijiazhuang,Hebei050031,China;3.SchoolofScience,JiangxiUniversityofScienceandTechnology,Ganzhou,Jiangxi341000,China) Multimodal optimization aims to search multiple optima (global and/or local optima) simultaneously,which gives rise to a challenging task for traditional optimization algorithms.This paper proposes a two-stage algorithm to solve multimodal optimization problems.In the first stage,NCDE with neighborhood mutation strategy tries its best to find as many approximate positions of optimal solutions as possible on the fitness landscape.After NCDE runs a certain number of iterations,DMC method is employed to divide the entire population into multiple clusters,and then CMA-ES algorithm is used to perform fine search on each cluster which is found by NCDE.Additionally,search point replenishment strategy is put forward to balance cluster size and to increase search capability of our algorithm in the beginning of the running.Extensive comparative experiments is made between our proposed approach and 9 state-of-the-art algorithms on two benchmark sets,the results show that the new algorithm is effective and superior to the other algorithms on the majority of test functions. crowding differential evolution;covariance matrix adaptation evolution strategy;multimodal optimization;niching;neighborhood mutation 2015-07-27;修回日期:2015-09-20;责任编辑:梅志强 国家自然科学基金(No.61364025,No.61402481);江西省自然科学基金(No.20151BAB217010);河北省自然科学基金(No.F2015403046);武汉大学软件工程国家重点实验室开放基金(No.SKLSE2014-10-04);河北省科学技术支撑项目(No.12210319) TP18 A 0372-2112 (2016)06-1481-094 实验设置与性能评价
5 实验结果分析


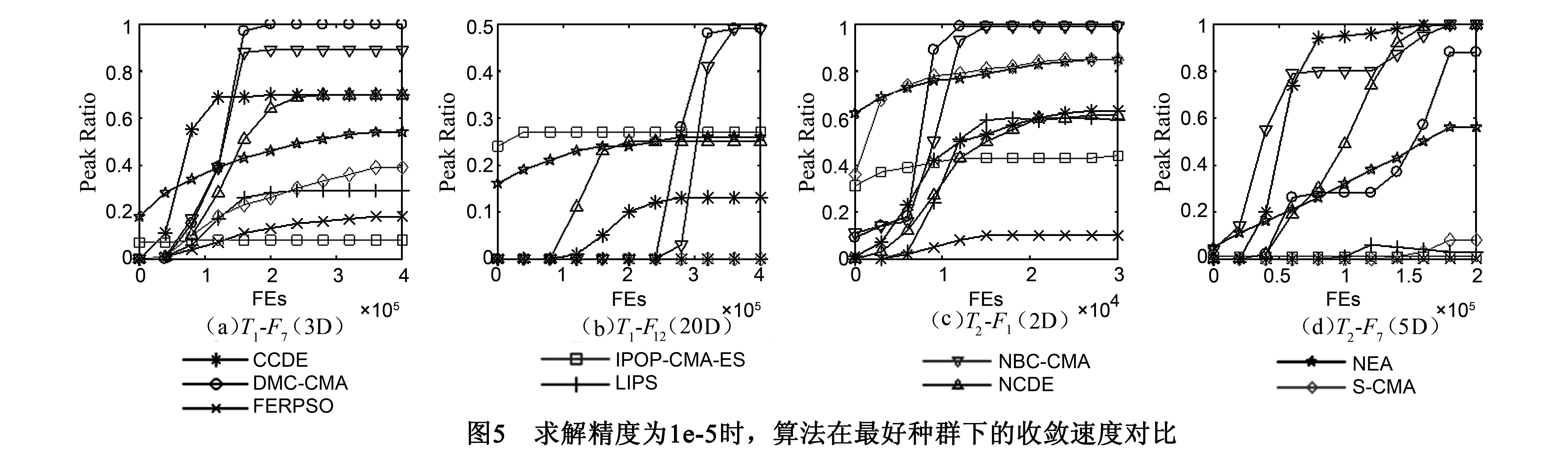
6 结论


