一种基于Duffing系统的信号检测与参数估计新方法

王慧武,丛　超

(哈尔滨电工仪表研究所,黑龙江哈尔滨 150028)



一种基于Duffing系统的信号检测与参数估计新方法

王慧武,丛超

(哈尔滨电工仪表研究所,黑龙江哈尔滨 150028)

为了给出一种基于Duffing系统的完整信号检测与估计方法,本文采用了耦合型间歇混沌振子,并引入了变尺度方法,以实现仅用单个Duffing振子完成对未知频率具有任意出相位的正弦信号的检测与频率估计.此外本文还提出了一种新的正弦信号幅值、相位同步估计方法,并综合方法原理和仿真实验结果证明了此方法具有估计精度高、抗噪声干扰能力强和实时性好的优点.最后用一组仿真实验结果验证了本文所提出的检测方法的有效性和估计方法的准确度.

混沌振子;变尺度;正弦信号检测;低信噪比;参数估计

1　引言

基于Duffing振子的弱信号检测方法是近年来得到快速发展的一种能在超低信噪比下有效检测弱信号的新方法,因其所采用的渐软斥力型Duffing方程同时具备了对微弱周期信号敏感和抗噪声干扰能力强的特性,所以此方法得到了各领域学者的广泛关注和深入研究[1].在基于Duffing振子的信号检测方面:1996年王冠宇[2]首次提出基于Duffing振子的信号检测方法,并给出了可行有效的检测模型;2003年李月等[3,4]通过引入高阶次非线性项和采用耦合振子,进一步提高了Duffing振子的抗噪声特性;2012年冷永刚[5]等通过引入变尺度方法,实现了在固定Duffing振子系统参数的条件下完成对任意频率信号检测.2014年李秀坤[6]等分析了不同内置策动力频率下的Duffing振子的弱信号检测灵敏度,并结合变尺度方法进一步增强了Duffing振子的弱信号检测性能.在应用Duffing振子进行信号参数估计方面的研究主要形成了两种思路:一种是应用间歇混沌振子列方法进行未知频率的信号参数估计[7～10],另一种方法则是在已知待测信号频率的条件下应用相态跃变型混沌振子对待测信号进行幅值和相位估计[11～15].

目前在基于Duffing振子的信号检测研究方面已有了较为成熟的方法,对信号的参数估计也有很多思路和尝试,但尚未有一种可以兼顾信号检测和完整参数估计的混沌振子类方法[16～18].针对这一问题,本文通过对现有混沌检测方法进行综合和改进,给出了一种变步长双耦合型间歇混沌振子,以实现仅用单个Duffing振子完成对任意频率待测信号的检测和频率估计.在此基础上本文还提出一种新的基于相态跃变型Duffng振子的信号幅值和相位同步估计方法,并通过一组仿真实验结果验证了综合以上两种方法可实现对频率未知具有任意初相位的正弦信号的有效检测和高精度参数估计.

2　基于变步长双耦合型间歇混沌振子的信号检测与频率估计

2.1双耦合型Duffing振子的系统特性

为了提高Duffing系统的弱信号检测性能,文献[5]提出了双耦合Duffing系统.双耦合Duffing系统利用两个单Duffing振子互相联系、互相控制的工作过程,提高系统在临界分岔处的稳定性,可以看做是一种高稳定性的改进型Duffing振子,其检测系统数学模型为:

(1)

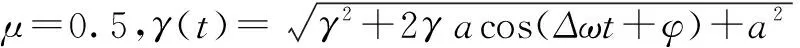
(2)

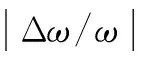
(1)以1.03为公比设定一组能够覆盖待测信号所在频段的系统求解步长序列an.

(2)通过MATLAB软件对Duffing系统进行编程仿真实现,将待测数据加入到Duffing系统内置策动力项中,并采用四阶龙格库塔数值解法对Duffing方程输出信号进行求解,根据步骤1所设定的系统求解步长序列依次调整计算步长.

(3)观察不同计算步长时的系统时域输出信号,若有某连续两次的时域输出为标准的间歇混沌状态,则表明在此两个步长对应的频段间存在待测信号.

由于上述变步长双耦合间歇混沌振子的检测准确性不受待测信号初相位的影响,所以理论上变步长双耦合型间歇混沌振子可以对未知频率具有任意出相位的正弦信号进行有效检测.

2.2对待测信号的频率估计

根据双耦合型Duffing振子的检测系统模型式(1),当把频率为ω0=ω+Δω的待测信号加入到检测系统中,并使系统输出间歇混沌信号时,系统策动力合力的幅值表达式为式(2),观察式(2)可知由于频差Δω的存在使得策动力幅值将以2π/Δω的周期进行变化,与之相应的系统输出的间歇混沌信号的周期时长T=2π/Δω.如果可以准确的测量系统输出的间歇混沌信号的周期T,就可以准确估算出待测信号频率.对于适应步长型间歇混沌振子,设采样频率为fs待测信号在步长为a0时可使系统输出间歇混沌信号,且Duffing系统输出的间歇混沌信号的一个周期长为T(T可通过测量系统时域输出信号确定),则待测信号的频率估计值为

ω1=a0fs(ω0+2π/T)

(3)

式(3)中ω0为系统内置信号角频率.

3　对待测信号幅值和相位的估计

为解决待测信号的幅值和相位的估计问题,本文提出了一种基于相态跃变型混沌振子的待测信号相位和幅值的同步估计方法,此方法的信号检测模型为

(4)

其中γ0cos(ωt+θ)为系统内置策动力(γ0略小于系统阈值γd),acos(ωt+φ)为待测信号,n(t)为噪声,此时的系统处于混沌临界态,当有同频信号加入到系统中时,系统即会跃入到大尺度周期态.理论上,Duffing振子进入大尺度周期态的条件为式(4)中的策动力幅值满足下式:

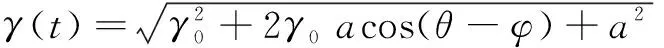
(5)

式(5)中γd为系统策动力阈值.如果用γa代表系统刚好由混沌态跃变到周期态的内置策动力幅值,则有

(6)

如果再建立起至少一个关于a和φ的类似式(6)的方程,则可通过求解二元函数方程组来对待测信号的幅值和相位进行估算.基于以上考虑,本文通过改变内置策动力的初相位来建立起关于a和φ的二元函数方程组,进而实现对待测信号幅值和相位的同步估计.具体方法为:首先根据待测信号频率估计结果对式(4)的系统参数进行设定,然后分别将待测信号加入到内置策动力初相位为0和π的检测系统中,再通过调整内置策动力幅值,并观察系统相态变化来确定每个检测系统发生相态跃变时的内置策动力值.如果用γ1和γ2分别代表初相位为0和π的检测系统的相态发生跃变时的内置策动力幅值,则关于相位φ和幅值a的2元2次方程组可表示为

(7)

对其求解可得

(8)

式(8)就是相位φ和幅值a的估计计算式.观察式(8)可知,此方法的估计准确度很依赖于检测系统对同频弱信号的灵敏度,为提高估计精度本文将系统内置信号角频率固定在0.4rad/s处,此条件下Duffing方程对微弱正弦信号的灵敏度最高,在检测信噪比低至-37dB的情况下仍可以准确分辨出幅度为0.001的正弦信号变化.

为了提高这种基于相态跃变型混沌振子的参数估计方法的实时性,并减少由观察相图产生的主观性及操作不便性,本文采用系统检测模型式(4)的类Halmition系统检测统计量:

(9)

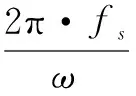
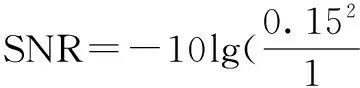
(1)将内置信号角频率固定在0.4rad/s,并将变尺度系数设定为待测信号频率.

(2)分别将待测信号加入到内置策动力初相位为0和π的检测系统中,并计算系统检测统计量,判断系统相态.

(3)通过编程实现下述功能:若检测统计量处于T1,则以0.001的变化幅度逐渐增大内置策动力幅值,直至系统检测统计量变为T2,输出并记下此时的内置策动力幅值γ;若系统检测统计量处于若检测统计量处于T2,则以0.001的变化幅度逐渐减小内置策动力幅值,直至系统检测统计量建委若检测统计量处于T1,输出并记下此时的内置策动力幅值γ.

(4)将初相位为0的检测系统相态跃变时的内置策动力幅值γ1和初相位为π的检测系统跃变时的内置策动力幅值γ2代入公式(8),计算待测信号幅值和相位的估计值.

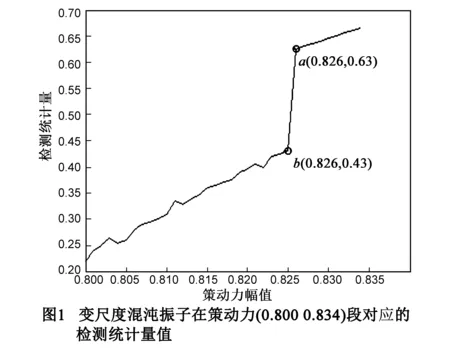
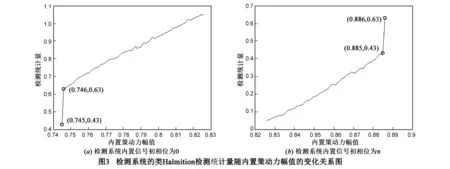
应用上述方法得到检测步骤3的输出为γ1=0.746,γ2=0.886.将γ1和γ2代入公式(8)算得待测信号的幅值和相位的估计值分别为0.149和1.034rad/s,相对估计误差分别为0.006和0.008.为了可以直观的显示检测系统的检测统计量变化规律,本文根据程序计算输出结果画出了检测统计量随内置策动力幅值的变化关系图,通过图3可明显观察到系统相态发生跃变时对应的的内置策动力幅值.

4　仿真实验

4.1信号检测与估计

为了验证变尺度双耦合型间歇混沌振子抗噪声干扰能力强、能对多频正弦信号进行准确检测与频率估计,以及混沌振子可以在低信噪比条件下对信号的幅值和相位进行高精度估计,设定仿真信号为

s(t)=0.5×cos(2π×10t+π/6)

+0.02cos(2π×50t+π/3)

+0.2×cos(2π×55t+π/4)+n(t).

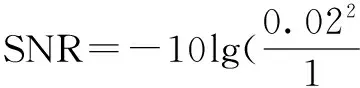
通过观察检测系统在预设的各求解步长处的时域输出信号,发现检测系统分别在系统求解步长a78和a79、a133和a134、a136和a137处输出了间歇混沌信号,其他步长均为混沌态输出，信号波形与图5输出信号相仿，图6～8为检测过程系统输出的间歇混沌信号.

综合图6提供的系统时域输出和变步长间歇混沌振子的判定标准可知,求解步长a78、a79间存在待测信号.由于加入检测系统中的待测信号是经过采样后的离散信号,所以输出信号的横坐标是采样点数,为了便于应用公式(3)对其进行频率估计,需要将其换算为相应的时间长度.在本例中,对于求解步长为an、采样长度为N的输出信号,其所对应的时间长度TN为

TN=an·N

(10)

每个待测信号对应两个有效检测步长,可任选一个步长处的输出信号对待测信号频率进行估计.此处以图6中(b)图(即系统求解步长为a79处的系统输出信号)为例,图6(b)中为3个完整周期的间歇混沌信号,通过观察用MATLAB工具放大后的系统时域输出信号测得一个周期的间歇混沌信号的总采样点数约为5180,将其依次带入式(10)和式(3)计算可得待测信号频率估计值为10.01Hz.

图7和图8分别为检测系统在求解步长a78和a79、a133和a134、a136和a137处连续输出的间歇混沌信号,由适应步长型间歇混沌振子的判定标准可知,在此相邻步长之间存在待测信号,并按照对图7中待测信号的估计步骤对检测出的信号进行频率估计,待测信号频率估计结果如表1.

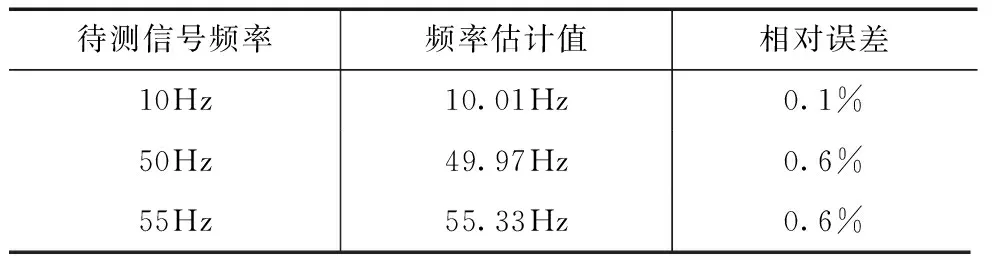
表1　信号频率估计结果

观察图6～8和表1可知,变尺度双耦合振子有效地检测出了待测信号中所包含的待测信号.表1为应用2.2节介绍的频率估计方法对待测信号的频率估计结果,由表中的频率估计结果可知可知,此方法的频率估计值具有较高的估计精度,在-34dB条件下频率估计值得相对误差仍可以达到10-3.

4.2对待测信号幅值和相位的估计

根据信号检测和频率估计结果再进行幅值和相位估计,具体步骤已在第3节进行了详细说明,此处不再重述.各待测信号幅值和相位参数的估计结果如表2,观察表中幅值和相位估计结果可知,此方法在噪声强度较高信噪比降到-34dB时仍可以对谐波信号进行有效检测,且参数估计相对误差可以稳定在10-2.

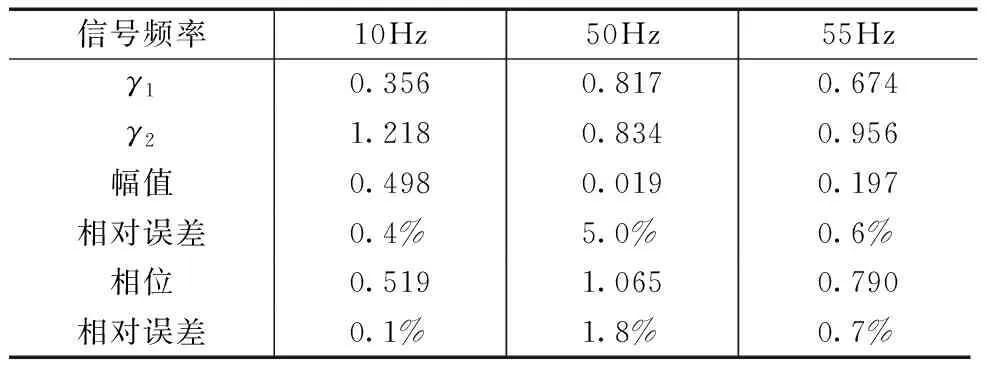
表2　信号幅值和相位估计结果

5　结论

本文提出了一种变尺度性双耦合间歇混沌振子,并给出了基于此方法的正弦信号频率估计公式,进而可以只用单个Duffing振子实现低信噪比下,对未知频率正弦信号的有效检测和高精度频率估计.

为了完成对信号幅值和相位的估计,本文还提出了一种基于相态跃变型混沌振子的针对已知频率正弦信号的幅值和相位同步估计方法,且为了减少由相图观察法带来的主观性、操作不便性并提高方法的实时性,采用了类Halmition检测统计量作为系统相变判据,并通过仿真实验结果证明了此方法在低信噪比下仍具有较高估计精度.

最后通过一组含有频率相近的正弦信号和低信噪比条件下的正弦信号的仿真数据的实验结果,验证了本文所提出的信号检测方法能够在低信噪比下,对未知频率具有任意初相位的正弦信号进行有效检测,且能有效分辨出频率相近的信号,以及本文所提出的参数估计方法在低信噪比条件下的有效性和高准确度.

[1]Guanyu Wang,Wei Zheng,Sailling He.Estimation of amplitude and phase of a weak signal by using the property of sensitive dependence initial conditions of a nonlinear oscillator[J].Signal Processing,2002,82:103-115.

[2]王冠宇,陶国良,陈行,等.混沌振子在强噪声背景信号检测中的应用[J].仪器仪表学报,1997,18(2):209-212.

Wang Guan-yu,Tao Liang-xing,Chen Xing,et al.Application of chaotic oscillators in the strong background noise in signal detection[J].Chinese Journal of Scientific Instrument,1997,18(2):209-212.(in Chinese)

[3]李月,石要武,马海涛,杨宝俊.湮没在色噪声背景下微弱微弱信号的混沌检测方法[J].电子学报,2004,32(1):87-90.

Li Yue,Shi Yaowu,Ma Haitao,Yang Baojun.Chaotic detection method for weak square wave signal submerged in colored noise [J].Acta Electronica Sinica,2004,32(1):87-90.(in Chinese)

[4]代理,李建,郑豫,孙涛.基于双耦合Duffing振子的随机相位正弦信号检测[J].成都信息工程学报,2008,23(1):50-53.

Dai Li,Li Jian,Zheng You,Sun Tao.Detection of phase randomly distributed weak sinusoidal based on double coupled Duffing oscillators[J].Journal of Chengdu University of Information Technology,2008,23(1):50-53.(in Chinese)

[5]李月,路鹏,杨宝俊,赵雪平.用一类特定的双耦合Duffing振子系统检测强色噪声背景下的周期信号[J].物理学报,2006,55(4):1672-1677.

Li Yue,Lu Peng,Yang Baojun,Zhao Xueping.Appling a special kind of two coupled Duffing oscillator to detect periodic signals under the background of strong colored noise[J].Acta Physics Sinca,2006,55(4):1672-1677.(in Chinese)

[6]丛超,李秀坤,宋阳,一种基于新型间歇混沌振子的舰船线谱检测方法[J].物理学报,2014,63(6):064301-064311.

Cong Chao,Li Xiukun,Song Yang.A ship line spectrum detection method based on intermittent chaotic oscillator model[J].Acta Physics Sinca,2014,63(6):064301-064311.(in Chinese)

[7]杨涛,陈治纲,邵惠鹤.一种可完全线性化的不同类型混沌系统同步方法[J].电子学报,2002,30(10).1-3.

Yang Tao,Chen Zhi-gang,Shao Hui-he.Synchronization of fully linearizable different chaotic systems[J].Acta Electronica Sinica,2002,30(10).1-3.(in Chinese)

[8]赖智慧,冷永刚,孙建桥,范胜波.基于Duffing振子的变尺度微弱特征信号检测方法研究[J].物理学报,2012,61(5):1-9.

Lai Zhihui,Leng Yonggang,Sun Jianqiao,Fan Shengbo.Study on detection method for weak signal based on variable scale Duffing oscillator[J].Acta Physics Sinica,2012,61(5):1-9.(in Chinese)

[9]刘海波,吴德伟.基于Duffing振子大尺度周期态相轨迹的频率测量方法{[J].电子学报,2013,41(10):2010-2015.

Liu Haibo,Wu Dewei.A new frequency measuring method by using Duffing oscillator’s phase trajectory in great periodic motion[J].Acta Electronica Sinica,2013,41(10):2010-2015.(in Chinese)

[10]葛晓慧,黄进.利用Duffing振子估计多频信号参数[J].浙江大学学报(工学版),2008,42(6):954-959.

Ge Xiaohui,Huang Jin.Parameter estimation of multi-frequency signal by using Duffing oscillator[J].Journal of Zhejiang University (Engineering Science),2008,42(6):954-959.(in Chinese)

[11]姜万禄，吴胜强，张建成.Duffing振子的两种信号检测微弱信号的方法及区别[J].燕山大学学报,2002,26(2):114-118.

Jiang Wan-lu,Wu Sheng-qiang,Zhang Jian-cheng.Two methods of weak signal detection of Duffing oscillator and their differences[J].Journal of Yanshan University,2002,26(2):114-118.(in Chinese)

[12]杨东升,李乐,杨珺,汪刚.基于双耦合混沌振子的未知频率信号检测[J].东北大学学报(自然科学版),2012,33(9):1726-1730.

Yang Dongsheng,Li Yue,Yang Jun,Wang Gang.Detection of the weak signal with unknown frequency based on the coupled chaos oscillator[J].Journal of Northeastern University (Natural Science),2012,33(9):1726-1730.(in Chinese)

[13]芮国胜,张洋,苗俊,等.联合增益递推的Duffing系统弱信号检测算法[J].电子学报,2012,40(6):1269-1273.

Rui Guo-sheng,Zhang Yang,Miao Jun,et al.A weak signal detection method by Duffing system with the gain[J].Acta Electronica Sinica,2012,40(6):1269-127.(in Chinese)

[14]Kennedy M K.Digital communications using chaos [ J].Signal Processing,2000,80:1307-1320.

[15]牛德智,陈长兴.Duffing振子微弱信号检测盲区消除及检测统计量构造[J].物理学报,2015,64(6):060503.

Niu Dezhi,Chen Changxing.Blind angle elimination method in weak signal detection with Duffing oscillator and construction of detection static[J].Acta Phys Sinica,2015,64(6):060503.(in Chinese)

[16]韩建群.一种减小Duffing系统可检测断续正弦信号频率范围的方法[J].电子学报,2013,41(4):733-738.

Han Jian-qun.A method of narrowing frequency range of intermittent sine signal detected by Duffing system[J].Acta Electronica Sinica,2013,41(4):733-738.(in Chinese)

[17]Haykin S,Li X B.Detection of signals in chaos[J].Processing of IEEE,1995,83(1):95-122.

[18]邓东虎,张群.Duffing振子在低信噪比雷达目标微弱特征提取中的应用[J].电子与信息学报,2014,36(2):453-458.

Deng Donghu,Zhang Qun.The application of Duffing oscillators to micro-motion feature extraction of radar target under low SNR[J].Journal of Electronics &Information Technology,2014,36(2):453-458.(in Chinese)

王慧武男,1968年出生,高级工程师,从事电能质量测试分析、电能计量的相关研究.

E-mail:c150484@126.com

丛超男,1989年出生,硕士,从事基于混沌理论的弱信号检测的研究.

E-mail:congchao-hrb@126.com

A New Signal Detection and Estimation Method by Using Duffing System

WANG Hui-wu,CONG Chao

(HarbinResearchInstituteofElectricalInstruments,Harbin,Heilongjiang150028,China)

In order to give a complete signal detection and estimation method based on Duffing system,this paper uses the coupling Duffing oscillator,and introduces the variable scale method,to detect and estimate the sinusoidal signal with unknown frequency and arbitrary phrase just by one Duffing oscillator.Besides,this paper puts forward a simplified method which is based on chaotic oscillator for estimating the amplitude and phase of the signal to be measured,and integrated method principle and the simulation experiment result proves that this method has high estimation precision,strong ability to resist noise interference and the advantages of good real-time performance.Finally,using a simulation result of a analog signal for verifying the availability and accuracy of the detection and estimation method is proposed.

chaotic oscillator;variable scale;sine signal detection;low signal to noise ratio;high precision estimation

2015-04-07;修回日期:2015-09-08；责任编辑：蓝红杰

国家科技部2014年度转制科研院所创新能力专项资金(No.2014EG119119)

TN911

A

0372-2112 (2016)06-1450-08