间歇混沌合成1/f噪声的相关特性分析

关　健,郜峰利,张　驰,曹军胜,张振国,郭树旭

(1.集成光电子学国家重点联合实验室吉林大学实验区,吉林大学电子科学与工程学院,吉林长春130012;2.中国科学院长春光学精密机械与物理研究所,吉林长春 130033)



间歇混沌合成1/f噪声的相关特性分析

关健1,郜峰利1,张驰1,曹军胜2,张振国1,郭树旭1

(1.集成光电子学国家重点联合实验室吉林大学实验区,吉林大学电子科学与工程学院,吉林长春130012;2.中国科学院长春光学精密机械与物理研究所,吉林长春 130033)

本文利用非线性随机微分方程来合成间歇混沌信号,针对该信号表现出的1/f噪声特征,在不同消失矩的小波基下进行相关特性分析.仿真结果发现,在功率谱的中间频段内,该信号的功率谱密度表现出典型的1/f噪声特性,其小波变换系数方差与相应的小波尺度呈对数线性关系;且在该频段内,部分尺度下该间歇性信号的小波变换系数的相关性随小波基的消失矩的增大而减小,在另一部分尺度下该相关性则随着消失矩的增大而增大.实验结果表明,随小波消失矩的增大,并非在所有尺度下小波变换对该间歇性信号均具有去相关作用.论文讨论了小波变换系数的方差和尺度的关系,详细分析了小波变换系数的相关性随小波消失矩的变化趋势.

间歇性;1/f噪声;小波变换;相关性;

1　引言

1/f噪声,也称为粉红噪声,是广泛存在于自然界中的一种非平稳随机过程[1],功率谱密度(Power Spectral Density,PSD)S(f)呈现出S(f)～A/fβ(0<β<2,β一般接近1)的形式的随机过程都可以认为是1/f噪声.1925年J B Johnson首次在真空电子管中发现了1/f噪声[2],随后人们在半导体器件中也发现了1/f噪声的存在,不仅如此,在很多系统中都能观察到1/f噪声,例如生物,物理,音乐,医学,股票,自然灾害等[2～8].虽然对1/f噪声的研究至今已有60年左右,但是对于1/f噪声的具体产生机制依旧没有一个确切的定论,现存的一些关于1/f噪声的模型往往也只能在某些系统中适用.然而对于1/f噪声特性的研究依然是一个十分热门的领域,特别是近年来人们发现半导体器件中产生的1/f噪声的特性与器件的质量和可靠性有着密切的关系,通过测量和研究半导体器件的1/f噪声特性可以成为一种有效评估半导体器件性能及其可靠性的无损检测手段[9,10].1/f噪声的长程相关性作为其重要特性之一,其研究也具有十分重要的学术意义和应用价值.

随着非线性科学中混沌理论的建立和应用[11,12],人们发现混沌理论中存在一种间歇混沌(intermittency)也可以产生1/f噪声[13].相比传统的合成法,利用间歇混沌来合成1/f噪声的频率指数可调性更强,同时能在很宽的频域内表现出1/f噪声特性.间歇混沌,是系统从规则有序转变到混沌状态的一种中间态,即系统时而表现出有序时而表现出随机混沌的一种状态.通常当系统的某些参数的变化突破某一临界值时,间歇混沌就出现了.最早Pomeau和Manneville提出了三种混沌间歇模型[14],后来相继出现了诱发激变型间歇混沌(crisis-induced intermittency)[15],含有不变子空间的非线性动力学系统中的on-off型间歇混沌[16,17]等.最近,又提出了用非线性随机微分方程(Stochastic Differential Equations,SDEs)产生间歇混沌以获取1/f噪声信号的方法[18～21].文献[21]中Ruseckas将SDEs结合非线性动力学系统,发现当横截L(Lyapunov)指数为零时,偏离不变子空间的偏移量的PSD能在较宽的频带内表现出1/fβ的特征.本文利用Ruseckas提出的方法合成间歇混沌信号,并利用小波变换对该合成信号进行分析,发现在表现出1/f噪声特性的频段内所对应的尺度与小波变换系数的方差呈对数线性关系;同时,并非所有尺度下小波变换对其均具有去相关性,仅在一部分尺度下,该合成信号的小波变换系数的相关性随小波基的消失矩的增大而减小,而在另一部分尺度下该相关性则随着消失矩的增大而增大.此外,当小波基消失矩一定时,小波变换系数的相关性均随尺度的增大而增大.论文针对这种方法合成的1/f噪声信号的上述特征进行了详尽的分析.

2　理论方法

2.11/f噪声信号的间歇混沌合成

对于一个有如下结构的二维映射[16]

xn+1=F(xn),yn+1=G(xn,yn)

(1)

对∀xn都有G(xn,0)≡0,因此y=0代表一个不定子空间.yn代表偏移不定子空间的偏移量.一般驱动变量xn是混沌的,横截L指数为

(2)

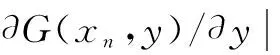
(3)

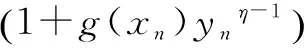
yn+1=wnyn，η>1

(4)

将式(4)两边取对数得到

sn+1=sn+zn

(5)

其中sn=lnyn,zn=lnwn,产生间歇性的临界条件为〈z〉=0.考虑到yn和sn之间的高度非线性关系能够产生间歇性,因此引入q指数,定义如下

(6)

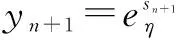
(7)

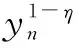
(8)

式(7)可转化为

(9)

其中,变量zn的计算由下式给出

(10)

理论上当〈z〉=0时,就能产生间歇性,这里取〈z〉=9×10-4,略大于0同时远远小于变量zn的标准差,这样就确保了一定能产生间歇性,方差〈(z-〈z〉)2〉=1,迭代驱动变量xn采用帐篷映射如下

(11)

其中〈x〉=0.5,〈(x-〈x〉)2〉=1/12,通过式(9)～(11)迭代n-1次后,就能产生长度为n的间歇性信号,由SDEs产生的信号的PSD具有1/fβ特性的部分的频率指数β可由下式得到[18,21,22]

(12)

这里ν=η=3,计算得β=1.

2.21/f噪声信号的小波系数相关性

1/f噪声在空间上具有分形特征,即自相似性,在时间上又具有长程相关性,信号中的每一点都蕴含着丰富的信息.对于常用分析信号谱的方法,比如傅里叶变换,在积分的过程中,可能丢失信号畸变点、突变点的大量信息,这将影响分析结果并得到不准确的结论.在以往分析信号的诸多方法中,应用比较广泛的小波分析,是一种十分有效地时频分析方法,且小波变换的多尺度特性,能准确的捕捉突变点的信息,其次小波也具有自相似性,这些特点使得小波比较适合用于分析1/f噪声的特性.因此合成间歇混沌信号之后,我们用不同消失矩的小波基对该信号进行小波分析.小波变换采用最常见的二进制小波变换,设1/f噪声信号y(t),y(t)∈L2(R),其小波变换系数的方差和尺度的关系为[23]

(13)

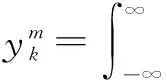
(14)

如果小波基具有N阶消失矩[23],即

Ψr(ω)=0,r=0,1,2,…,N-1

(15)

此时ω是Ψ(ω)的N阶零点,记为Ψ(ω)=ωNΨ0(ω)

代入式(14)可进一步得到

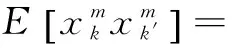
(16)

N为小波消失矩,从式(16)可以看出当频率因子β,k-k′和尺度m一定,且满足2N+1>β时,E和消失矩N的关系主要由(k-k′)2N-β+1和|ω|2N-β两项决定,随着消失矩的增大,(k-k′)2N-β+1项使得相关性E减小,然而|ω|2N-β项则会使相关性E增大,即E的变化趋势主要受(k-k′)2N-β+1和|ω|2N-β两项权重的影响.

3　仿真实验结果

利用迭代公式(9)产生长度n=223的间歇信号yn如图1所示,其中图1(a)为时域波形,图1(b)为信号yn1000个PSD进行平均的结果.从图1(a)可以看出生成的信号是稳定和爆发态交替出现的,说明生成的信号具有间歇混沌信号的典型特征.从图1(b)中可以看出平均PSD在中间很宽的一段频率范围内表现出1/f噪声的特性,其大概频率范围为10-5f10-1.5,图中的虚线部分则为该频段范围的线性拟合曲线,斜率k=-0.977,这与之前理论部分计算的β=1相当接近,说明生成的间歇性信号是正确的,且在中间频段内表现出了我们所需要的1/f噪声特性.

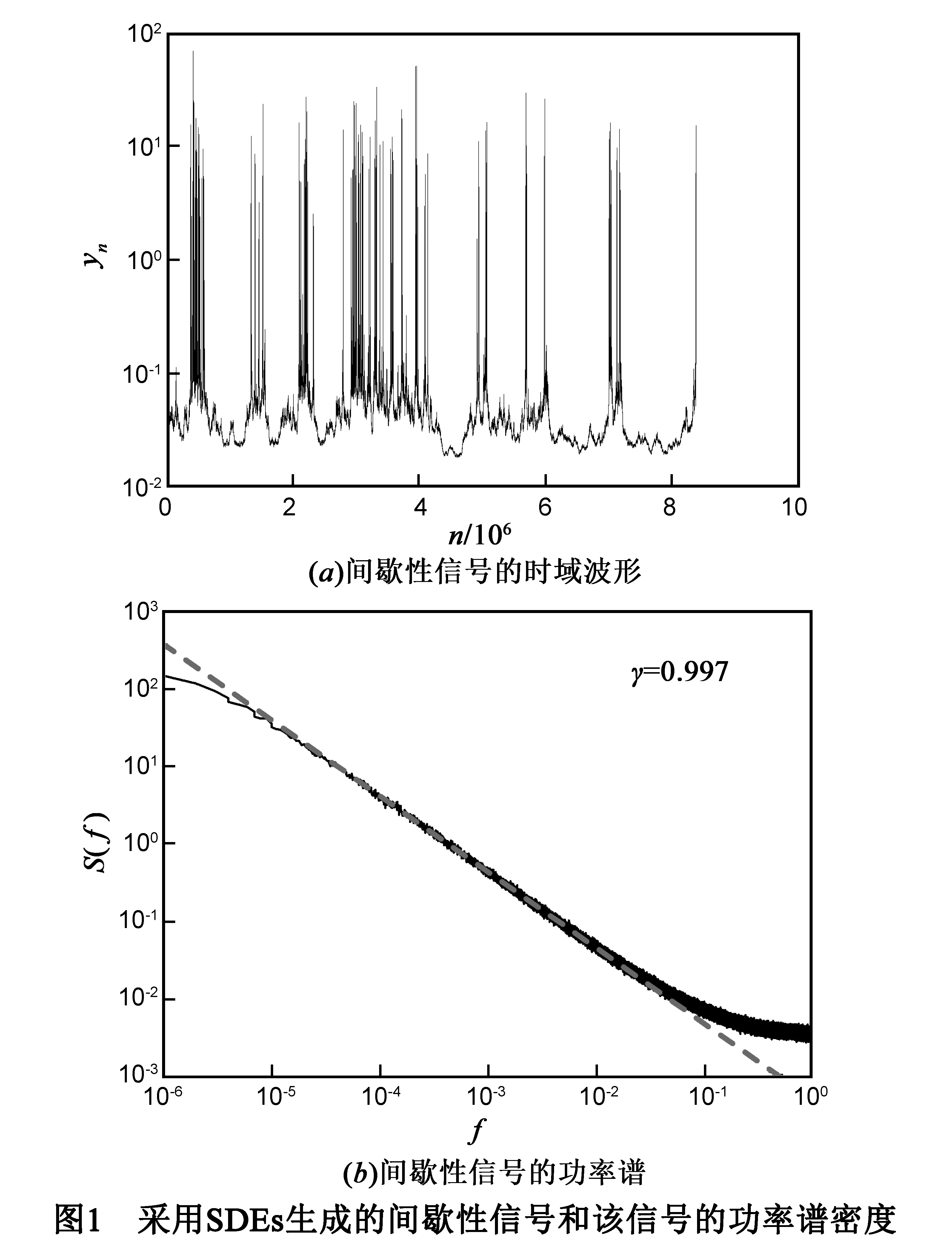
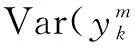
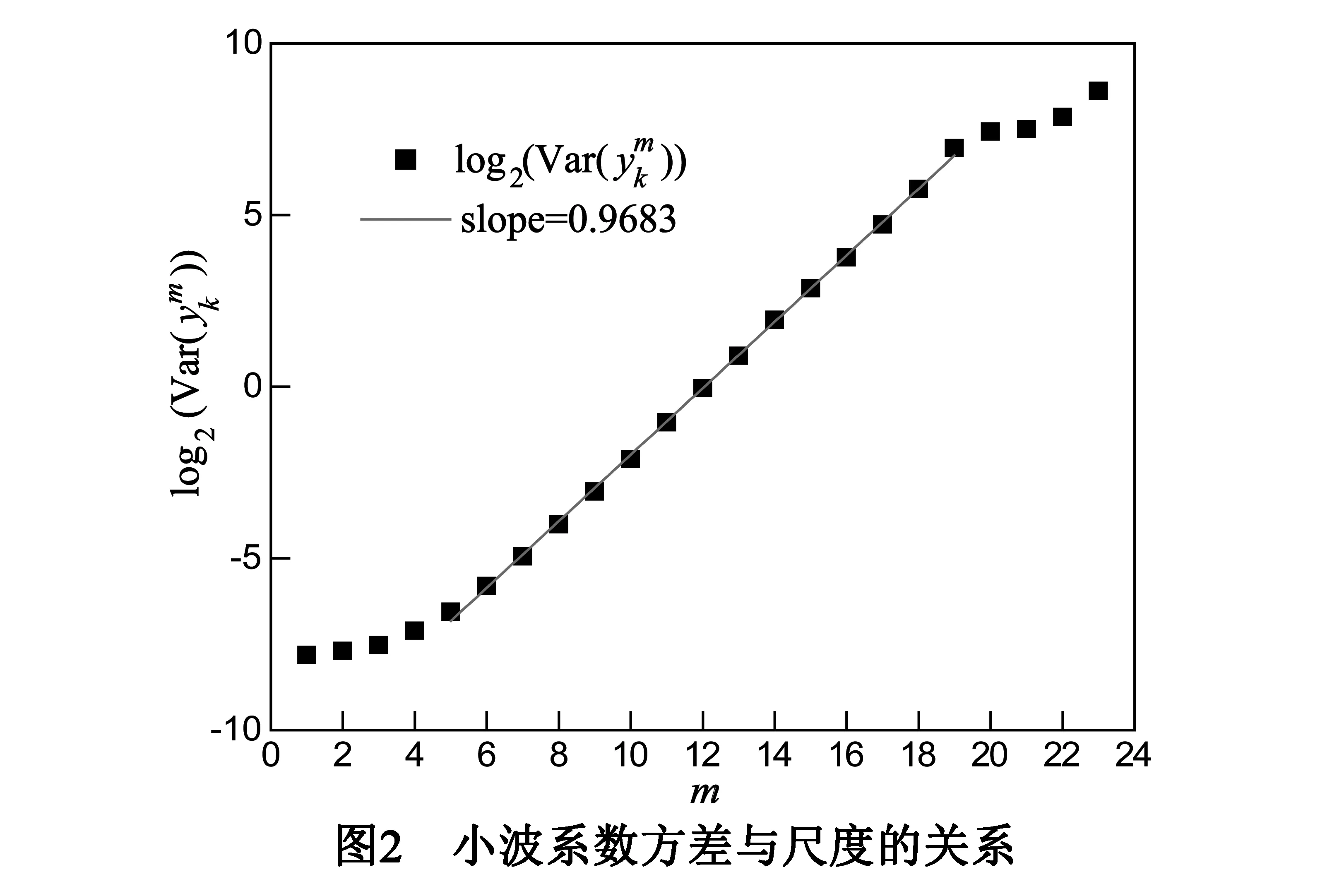
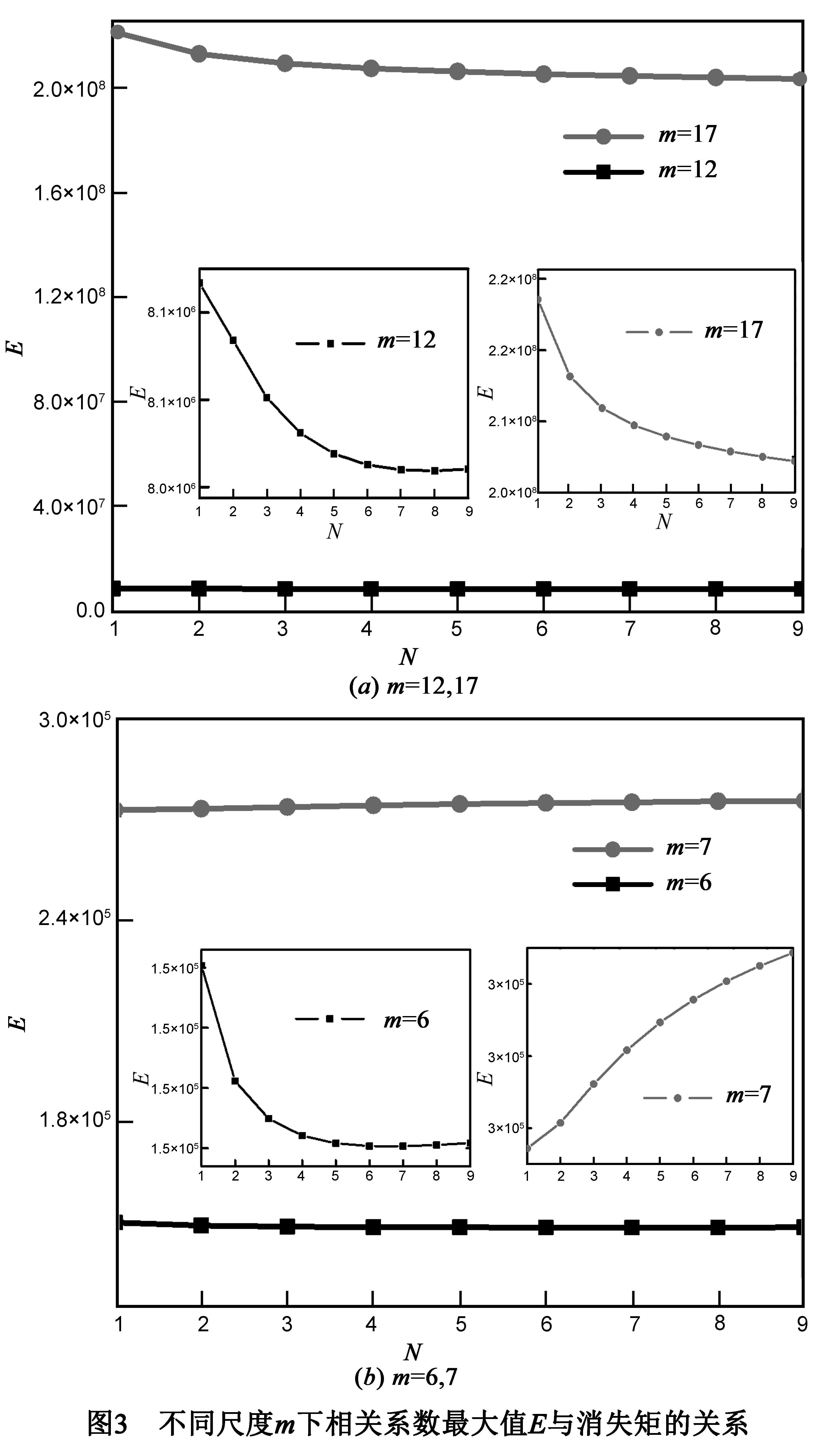
为了分析小波变换对间歇性信号产生的1/f噪声的相关性的影响,在具有不同消失矩的db小波基下对该间歇性信号yn做二进小波变换得到相应的小波变换系数,然后对所得小波变换系数做自相关运算,由于计算机内存的限制,消失矩N取1～9.为了表征相关函数序列整体相关性的大小,计算相关性函数序列的最大值E,通过式(16)即可获得不同尺度下E与所选小波基的消失矩N的关系.从所有尺度中选取部分尺度下的结果如图3所示,其中图3(a)为m=12,17的结果,图3(b)为m=6,7的结果,内嵌图分别为所对应曲线的放大图.从图3(a)中可以看出,相关性E随着消失矩N的增大而呈缓慢下降的趋势,且下降的趋势越来越小.说明在尺度m=12,17下小波变换具有去相关性的作用.而从图3(b)中可以看出,当m=6时,相关性E先随着消失矩N的增大而迅速下降随后有略微增大的趋势,但增大的程度十分微弱,整体仍然呈现相关性减小的趋势;而当m=7时,相关性E随着消失矩N的增大而逐渐增大,此时小波变换具有增强相关性的作用.计算结果显示,在尺度:1、3、4、5、6、8、10、12、17、18、21下,相关性随消失矩的增大而减小;而在尺度:2、7、9、11、13、14、15、16、19、20、22、23下,相关性随消失矩的增大而增大.图3现象可由式(16)进行解释,尺度m=6,12,17下的积分项系数对相关性的影响起主要作用,而在尺度m=7下的积分项对相关性的影响起主要作用.上述现象表明,在部分尺度下小波变化系数的相关性E随消失矩N的增大而减小,即小波变化对1/f噪声具有去相关性的作用,而在另一些尺度下小波变化系数的相关性E又随着N的增大有增大的趋势,所以并非在所有尺度下小波变换对该间歇性信号产生的1/f噪声均具有去相关性的作用.此外,当消失矩N固定时小波变换的尺度m越大,对应的小波系数之间的相关性E越大,这是由于在小波空间分解1/f类分形信号,大尺度对应其低频部分的小波变换系数,而根据1/f类分形信号的频谱定义式(1),频率越低1/f类分形信号的强度越大,故大尺度下的小波变换系数之间的相关性就越大.

4　结束语

本文对非线性随机微分方程产生的间歇性信号的1/f特性进行了分析,仿真实验首先利用随机微分方程合成间歇性信号,其功率谱密度在中间较宽的频段范围内表现出了1/f噪声的典型特性.然后采用不同消失矩的小波基对该间歇性信号进行小波变换,分别计算了不同尺度下小波变换系数的相关性和方差,结果显示,间歇性信号的PSD表现出1/f噪声特性的频段内所对应的尺度与小波变换系数方差的呈对数线性关系;此外在一部分尺度下该间歇性信号的小波变换系数的相关性随小波基的消失矩的增大而衰减,在另一部分尺度下该相关性则随着消失矩的增大而增大,证明了小波变换并非在所有尺度下对该间歇性信号产生的1/f噪声均起到去相关性的作用.此外,当小波基消失矩一定时,小波变换系数的相关性均随尺度的增大而增大.

[1]Keshner M S.1/fnoise[J].Proceedings of the IEEE,1982,70(3):212-218.

[2]Johnson J B.The Schottky effect in low frequency circuits[J].Physical Review,1925,26(1):71.

[3]Balandin A A.Low-frequency 1/fnoise in graphene devices[J].Nature Nanotechnology,2013,8(8):549-555.

[4]Hausdorff J M,Peng C K.Multiscaled randomness:A possible source of 1/fnoise in biology[J].Physical Review E,1996,54(2):2154.

[5]Hooge F N.1/fnoise sources[J].Electron Devices,IEEE Transactions on,1994,41(11):1926-1935.

[6]Voss R F,Clarke J.“1/fnoise” in music:Music from 1/fnoise[J].The Journal of the Acoustical Society of America,1978,63(1):258-263.

[7]Campbell M J,Jones B W.Cyclic changes in insulin needs of an unstable diabetic[J].Science,1972,177(4052):889-891.

[8]Mandelbrot B B,Van Ness J W.Fractional Brownian motions,fractional noises and applications[J].SIAM Review,1968,10(4):422-437.

[9]Vandamme L K J,Alabedra R,Zommiti M.1/fnoise as a reliability estimation for solar cells[J].Solid-State Electronics,1983,26(7):671-674.

[10]Vandamme L K J.Noise as a diagnostic tool for quality and reliability of electronic devices[J].Electron Devices,IEEE Transactions on,1994,41(11):2176-2187.

[11]杨爱波,王基,刘树勇,等.基于空间栅格法的最大Lyapunov指数算法研究[J].电子学报,2012,40(9):1871-1875.

YANG Ai-bo,WANG Ji,LIU Shu-yong,et al.Analgorithm for computing the largest Lyapunov exponent based on space grid method[J].Acta Electronica Sinica,2012,40(9):1871-1875.(in Chinese)

[12]温祥西,孟相如,马志强,等.小时间尺度网络流量混沌性分析及趋势预测[J].电子学报,2012,40(8):1609-1616.

WEN Xiang-xi,MENG Xiang-ru,MA Zhi-qiang,et al.Thechaotic analysis and trend prediction on small-time scale network traffic[J].Acta Electronica Sinica,2012,40(9):1871-1875.(in Chinese)

[13]Niemann M,Kantz H,Barkai E.Fluctuations of 1/fnoise and the low-frequency cutoff paradox[J].Physical Review Letters,2013,110(14):140603.

[14]Pomeau Y,Manneville P.Intermittent transition to turbulence in dissipative dynamical systems[J].Communications in Mathematical Physics,1980,74(2):189-197.

[15]Grebogi C,Ott E,Romeiras F,et al.Critical exponents for crisis-induced intermittency[J].Physical Review A,1987,36(11):5365.

[16]Platt N,Spiegel E A,Tresser C.On-off intermittency:A mechanism for bursting[J].Physical Review Letters,1993,70(3):279.

[17]Heagy J F,Platt N,Hammel S M.Characterization of on-off intermittency[J].Physical Review E,1994,49(2):1140.

[18]Kaulakys B,Ruseckas J,Gontis V,et al.Nonlinear stochastic models of 1/fnoise and power-law distributions[J].Physica A:Statistical Mechanics and its Applications,2006,365(1):217-221.

[19]Kaulakys B,Alaburda M.Modeling scaled processes and 1/fβnoiseusingnonlinearstochasticdifferentialequations[J].JournalofStatisticalMechanics:TheoryandExperiment,2009,2009(02):P02051.

[20]Ruseckas J,Kaulakys B.1/fnoise from nonlinear stochastic differential equations[J].Physical Review E,2010,81(3):031105.

[21]Ruseckas J,Kaulakys B.Intermittency in relation with 1/fnoise and stochastic differential equations[J].Chaos:An Interdisciplinary Journal of Nonlinear Science,2013,23(2):023102.

[22]Kaulakys B,Ruseckas J.Stochastic nonlinear differential equation generating 1/fnoise[J].Physical Review E,2004,70(2):020101.

[23]Wornell G W,Oppenheim A V.Wavelet-based representations for a class of self-similar signals with application to fractal modulation[J].Information Theory,IEEE Transactions on,1992,38(2):785-800.

关健男,1990年7月生,吉林长春人,现为吉林大学电子科学与工程学院研究生,目前主要从事半导体激光器1/f噪声特性研究.

E-mail:guanjian14@jlu.edu.cn

郜峰利(通信作者)男,1977年11月生,河南沁阳人,现为吉林大学电子科学与工程学院副教授.主要从事半导体激光器噪声特性及其应用方面的研究.

E-mail:gaofl@jlu.edu.cn

Analysis of Correlation Characteristics of 1/f Noise Generated by Intermittency

GUAN Jian1,GAO Feng-li1,ZHANG Chi1,CAO Jun-sheng2,ZHANG Zhen-guo1,GUO Shu-xu1

(1.StateKeyLaboratoryonIntegratedOptoelectronics,CollegeofElectronicScienceandEngineering,JilinUniversity,Changchun,Jilin130012,China;2.ChangchunInstituteofOptics,FineMechanicsandPhysics,ChineseAcademyofSciences,Changchun,Jilin130033,China)

In this paper the nonlinear stochastic differential equation is used to generalize an intermittency signal,and the correlation of its 1/fnoise characteristics under the wavelet bases with different vanishing moments are analyzed.The simulation results show that in the middle band of the frequency spectrum,its power spectrum density (PSD) shows typical 1/fnoise characteristics,and the relationship of the signal’s wavelet transformation coefficient variance and the corresponding wavelet scale is linear under logarithm coordinate.In this frequency band,under some scales the signal’s wavelet transformation coefficient correlations decrease with the vanishing moments growing,while in other scales,the correlations increase with the vanishing moment increasement.These results indicate that wavelet transformation does not always bring decorrelation to the intermittency signal.The relationship of the wavelet transformation coefficients’ variances and the scale,and the tendency of coefficients’ correlations with wavelet vanishing moments changing are analyzed.

intermittency;1/fnoise;wavelet transformation;correlation;

2014-12-09;修回日期:2015-01-22;责任编辑:梅志强

国家自然科学基金青年科学基金(No.61204055);吉林省科技发展计划青年科研基金(No.20130522188JH);吉林省科技发展计划自然科学基金(No.20140101175JC)

TN911.6

A

0372-2112 (2016)06-1389-05