多处理器片上系统中一种结合二阶导数的温度预测模型

魏　琳,周　磊,吴　宁,杨　睛

(1.扬州大学信息工程学院,江苏扬州 225000;2.南京航空航天大学电子信息工程学院,江苏南京 210016)



多处理器片上系统中一种结合二阶导数的温度预测模型

魏琳1,周磊1,吴宁2,杨睛1

(1.扬州大学信息工程学院,江苏扬州 225000;2.南京航空航天大学电子信息工程学院,江苏南京 210016)

区域温度预测是多处理器片上系统(MultiProcessor System-on-Chips,MPSoCs)高效散热的基础.本文以RC 热传导(Thermal Resistance and Capacitance,Thermal RC)模型为基础,结合二阶导数提出了一种温度预测模型.该模型不仅可以在较低的运算复杂度下准确预测温度,而且能在固定的预测误差率范围内拓宽预测时间长度,进而减少模型在实际运行中被调用的次数,降低额外功耗.实验结果表明,相比现有的一次导数预测模型,在相同可接受误差率范围内,该模型能将预测时长拓宽至对比模型的1.6倍.同时,当预测时长拓展至2.5s时,该模型的预测准确率比对比模型高3.84%.

多处理器片上系统(MPSoCs);RC热传导模型;温度预测模型

1　引言

随着集成电路技术的发展,传统全局互连方式(总线互连)已无法适应当前多处理器片上系统(MPSoCs)的通信需求.因此,结合片上网络(NoC)结构设计的新兴MPSoCs随之涌现,该设计可以提供更大的互连带宽,更低的网络能耗和更高的晶体管密度以实现更高的性能[1～3].然而,较大的晶体管密度及不断提高的处理器工作频率使芯片内功耗加大,导致MPSoCs中处理器过热[4～6].高温不仅使系统中的互连延迟、功耗、冷却成本和封装成本增加,而且会影响电路的可靠性[7,8].因此,建立高效精确的温度模型以解决散热问题是必要的.

相比于实时温度感知,温度预测可以提前为温度管理机制[9,10]提供温度信息以便做出相应的降温决策.因此,温度预测是温度管理机制实现高效散热优化的基础.目前,主要通过如下两类方法来预测温度,一类是软件方法[11～13].如文献[11]中Coskun A K等人利用自回归移动平均预测建模和查找温度表的方法提出了一种预测方案.文献[13]中Xiaorui Wang等人提出了一种线上预估模型以保证预测准确性和系统的稳定性.但这类方法计算复杂度较高,这无疑消耗了大量的时间和功耗,容易形成新的热区.另一类方法以简化热传导模型(Compact Thermal Model,CTM)[6]为基础实现温度预测[14～17].相比于软件方法,这种方法具有较低的分析复杂度.如文献[14]中Inchoon Yeo等人结合基于应用的温度模型(Application-Based Thermal Model,ABTM)和基于处理器核的温度模型(Core-Based Thermal Model,CBTM)两种模型提出了一种多核系统中的预测模型.然而,两个模型之间的比例系数需要根据工作的负载调整,考虑到系统负载的不稳定性,该模型在复杂的实际情况下很难快速地预测温度.文献[17]中Kun-Chih Chen等人提出了一种基于RC热传导模型的低运算复杂度的温度预测模型.然而,其中所利用的一阶导数由于忽略了温度变化的速度即温度变化过程中的非线性特点,所以在可接受的误差率范围内它能预测的时间宽度较窄.同样,在较大的预测时间间隔内,该模型预测的准确性也会急剧降低.

为解决以上问题,本文从拓宽预测时长的角度出发,结合二阶导数提出了一种基于RC热传导模型的温度预测模型,该预测模型可以拓宽预测时间宽度以减少运行中模块被调用的次数,继而减少额外功耗.以文献[17]中提出的温度预测模型为基础,利用二阶导数在此基础上进行了改进,从而达到延长预测时长的目的.

2　温度预测模型

2.1RC热传导模型

集成电路内部的热量是由功耗产生的.傅里叶导热定律指出,物体冷却的速率与物体和环境之间的温度差成正比[18].结合傅里叶定律和热力学第一定律可以得到单位时间内的温度变化的公式如下

(1)

其中T(t)和P(t)分别是时间t时的温度和处理器节点的功率.R和C是所在区域的热阻和热容.其中R与所处材料层的厚度,材料的热导率,传热系数以及散热横截面积参数相关;C与所处材料层的厚度,材料的比热,材料密度以及散热横截面积参数有关[6].等式(1)是一个经典的线性微分等式,因此,T(t)和P(t)之间的关系可以改写得到如下等式

(2)

为了简化公式,假设在一段时间内处理器核以平均功率运行,即P(t)为常数Pc.其中T0为t0时刻的温度,T0=T(t0),即对处理器进行预测的初始温度,是运行期间的一种极限状态.将等式(2)积分得到如下等式

(3)

其中b=1/(RC),即一个与具体应用无关,只与硬件材料结构和平面布局有关的物理常数.本文基于实验的工作平台HotSpot 5.0[19]根据处理器核在平面布局中的具体位置对b分别选取了不同取值.

由式(3)可以看出,温度随时间增加是呈指数变化上升的,即是非线性的.文献[17]采用一阶导数来推导温度预测模型,忽略了温度的非线性特性,预测值与实际值之间的误差率会随着时间的增加而逐渐增大.相比于一阶导数,二阶导数可以考虑到温度非线性的特点,在原有线性变化的基础上作出调整.因此,采用二阶导数推导的模型更符合实际温度的变化.

2.2结合二阶导数的温度预测模型

采用二阶导数来推导预测温度T(t)和时间t之间的关系式,首先要得到式(3)的一阶导数,它可以表示为

(4)

对一阶导数式(4)再进行求导得到的二阶导数,可以表示为

(5)

求得的二阶导数反映了当前时间点t相对于上一个时间点(t-Δt)之间的温度变化的速率.因此,时间点(t+Δt)与相应的上个时间点t之间的温度变化的速率可以用时间点(t+Δt)上的二阶导数表示

(6)

因此,温度在时间点(t+Δt)上的变化值可以结合时间点t的变化值与(t+Δt)的温度变化的速率表示为

(7)

按此类推,时间点(t+kΔt)上的温度变化值可以表示为

(8)

其中k是一个常数,代表预测的最小时间间隔数.然后,将所有时间点上的温度变量累计起来得到总的预测温度变化量,即当前时间和预测时间之间的温度变化量,它可以表示为

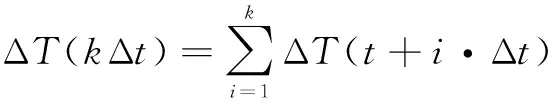
(9)

将它全部展开为

ΔT(kΔt)=(k·e-bΔt·Δt+(k-1)·e-2bΔt·Δt+…+

(10)

预测时间点(t+kΔt)的温度可以计算如下所示

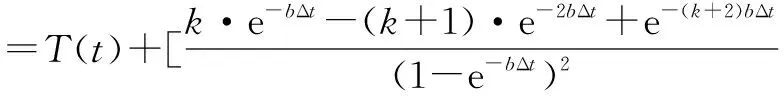
(11)

具体分析的时间/温度曲线图如图1所示.虽然式(11)比较复杂,但是当常数k确定后计算复杂度仍然保持为O(1).由式(11)可见,要得到最终的预测温度T(t+kΔt),除了预测温度变量ΔT(kΔt),当前温度T(t)也是一个重要的参数.在简化热传导模型(CTM)中,根据温度与热阻、功耗之间的关系,T(t)可以由如下等式求得[20]:

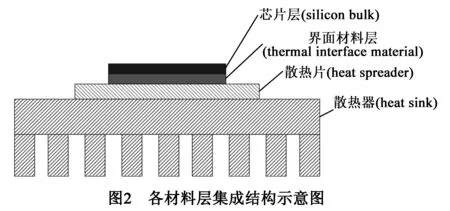
(12)其中TAmb是一个固定的环境温度,值得注意的是此处的环境温度并不是室温,而是在芯片封装中的温度,在散热设计中一般设置其为45℃[19].A为垂直于热流方向的横截面积,即有效散热面积.在混合集成系统中,横向相邻节点之间的水平散热截面积要远小于垂直方向的散热面积,从而,大部分的热消散主要集中在垂直方向上.文献[21]证明90%的热量是从芯片层(Si层)向散热器层传播的,即按垂直方向散热,具体集成结构如图2所示.因此,此处的A设为垂直方向上的散热面积,即各个区域的表面积.R是该区域的热阻,包括芯片层热阻,界面材料热阻,散热片热阻和散热器热阻以及对流热阻.内热阻Rin与所处层材料的热导率K和该层的厚度L以及相应的散热面积A有关,即R’=L/K·A.因此,

(13)

其中,P为在相应条件下给定的功率.TDie,Tsink分别为芯片温度和散热器温度,本实验中其均可以从HotSpot软件中得到.对流热阻用如下等式计算

Rconv=1/(h·A)=(Tsink-TAmb)/P

(14)

其中,h为传热系数.因此,R=Rin+Rconv.Pprocessor是当前节点的处理器功耗,由节点中处理器本身的结构和所执行的任务决定,因此Pprocessor可由节点本身所包含的功耗监控组件获得.Prouter表示该节点路由器功耗,由通信功耗和路由单元结构功耗两部分构成.其中,通信功耗主要由链路数据传输产生,结构功耗主要由数据传输时路由单元内部的交叉开关、仲裁机构以及缓存产生.两者都与经过路由单元的流量v相关,因此Prouter可以表示为:

(15)

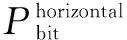
T(t+kΔt)=T(t)+ΔT(kΔt)

(16)

3　实验结果

3.1实验环境

在实验中,为了证实本文预测模型的有效性,本文采用一台PC机作为实验设备,其CPU配置为Inter Core 2 Duo CPU,主频为2.00GHz,内存为1.99GB.并将HotSpot 5.0 软件作为实验的仿真平台,HotSpot是利用材料电、热之间的二元性来模拟得到处理器的温度[19],其预测温度更接近实际的温度.文献[6]中证实Hotspot软件测得的温度值与实际温度传感器测量得到的温度值误差在0.2℃以内.因此可以默认由HotSpot 得到的温度为实际温度.为了简化比较仿真结果和预测结果,整个平面被划分为16块(4×4 2-D Mesh),其中所有模块的材料参数和功率值都相等.HotSpot中设置的各材料层的参数如表1所示[19].

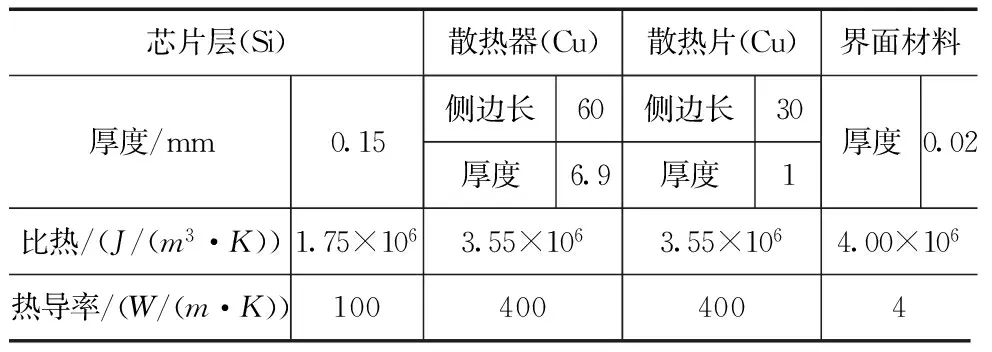
表1　各层材料参数

在HotSpot平台中可直接设置每个区域块的总功耗,即P=Pprocessor+Prouter.区域中各条边上的热阻可以认为是相邻区域的总热阻R[6].由于各个区域相处的平面位置不同,每个区域中各条边的接触环境也不相同,即各条边的热阻不同,从而区域的总热阻R不同.由于本实验中平面布局的对称性,所有区域块可以分为三个对称的区域组,如图3所示.因此,针对不同的区域位置共有3个不同的参数b值,本实验在三个对称区域组中分别选取一个区域块来进行实验对比,这其中包括L2,L2-left和Bpred0,其参数b分别为0.21,0.18 和0.25.各区域参数b的值可直接由HotSpot 5.0软件中的计算模型根据实验中划分的平面布局和设置的各层材料参数得出[19].为了对比模型性能,本文重构了由一阶导数推得的温度预测模型以做比较.3.2实验结果

3.2.1预测窗口长度

为了得到两种模型的预测窗口,统一设置预测最小时间间隔为0.1s,并将时间宽度放宽至3s.分别在四种不同的功率条件下(45W,55W,60W,75W)比较两种模型的温度预测曲线与实际温度曲线之间的偏差,得到的预测结果如图4所示.用预测值与实际值之间的误差率来评定偏离度大小,并将阈值设置为0.6%(约0.7℃),从而得到两种预测方法在不同功率条件下的预测窗口,如表2、表3所示.注意,只要有一个区域块的误差率超过0.6%这一组数据都无效.将两种模型的四个预测窗口求平均最终得到,由一次导数推得的模型的预测窗口为[0s～1s],本模型的预测窗口为[0s～2.6s].显然,在相同的误差率限制条件下,本模型具有较长的预测窗口长度.

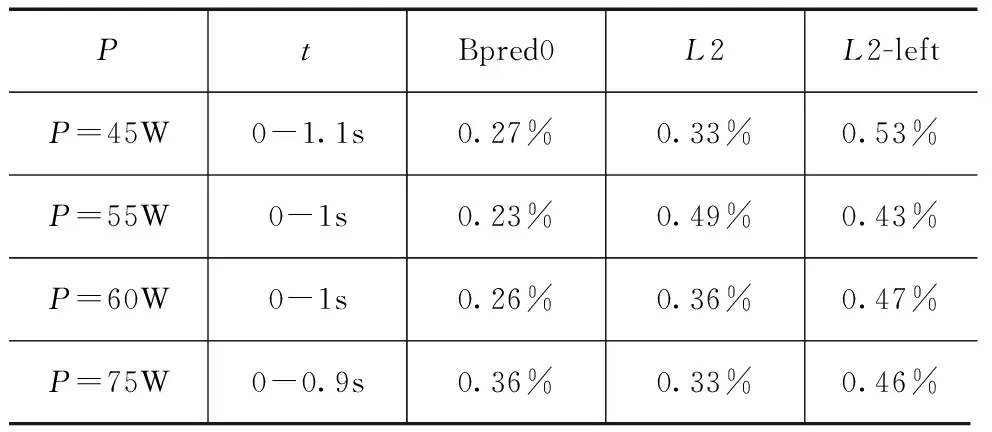
表2　误差率阈值为0.6%时一次导模型的预测时间窗口宽度

表3　误差率阈值为0.6%时本模型的预测时间窗口宽度

3.2.2预测准确度

为了验证本模型预测的准确性,实验中选取两个预测时长,分别为1.5s和2.5s,在这两种条件下比较不同区域块上两种模型的误差率以此衡量预测的准确度.从图5可以看出,一次导数推得的模型的误差率普遍高于本模型的误差率,当预测时长为1.5s时,两者的误差率最大相差2.08%.当预测时长拓展至2.5s时,一次导数模型的误差率与本模型对应的误差率相比最大超过3.84%,与1.5s时长下的误差率相比上升了84.6%.可见,在较长的预测时长下,本模型比一次导数推得的模型具有更高的预测准确度.

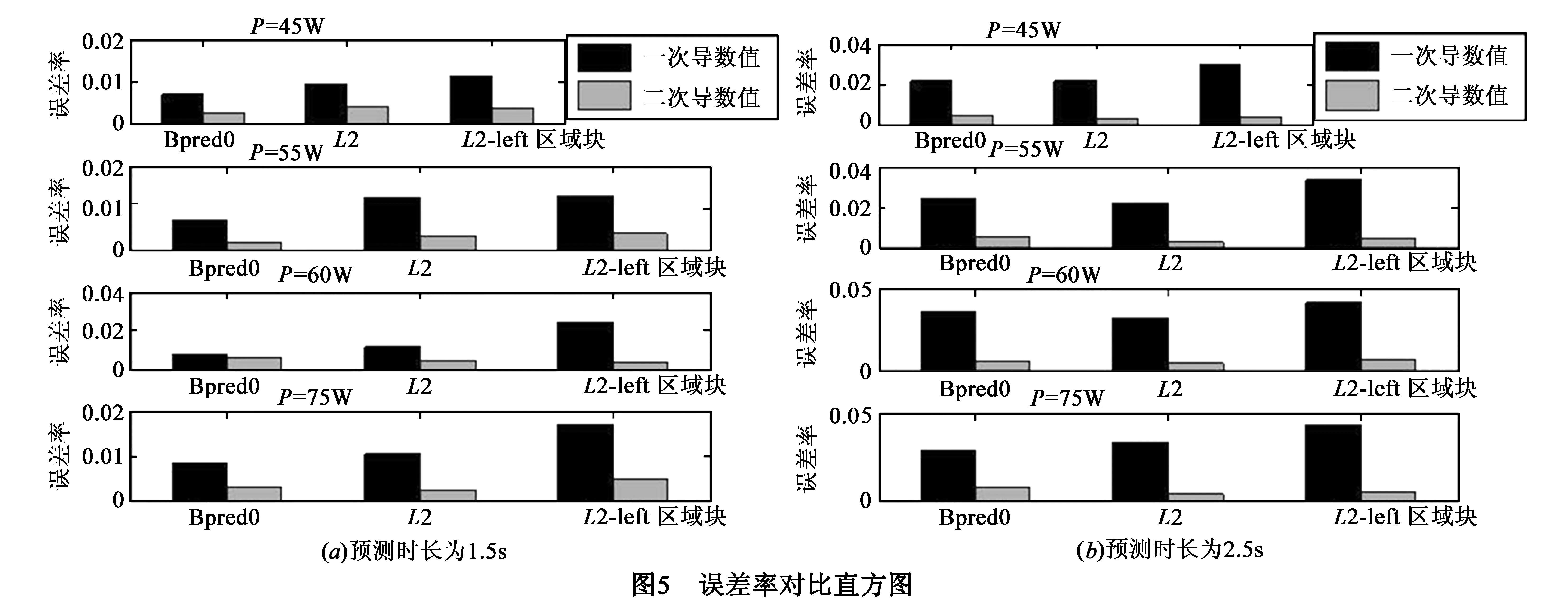
4　结论

在本文中,从拓宽预测时间长度这个角度出发,结合二阶导数提出了一种基于RC热传导模型的温度预测模型.实验结果表明,相比于一阶导数得到的模型,本模型可以将预测时间长度从1s拓宽至2.6s.当预测时间较长时,本模型具有更好的预测准确性.因此,在可接受的预测误差范围内,本模型的预测时间更长,性能更优.在进一步的工作中,我们将采用基于多播传输的温度信息共享策略实现全局温度信息的高效传递.

[1]Jabbar M H,M′zah A,Hammami O,et al.Exploration of 2D EDA tool impact on the 3D MPSoC architectures performance[A].Masahiro Fujita.Proceedings of the Fifth Asia Symposium on Quality Electronic Design (ASQED)[C].Penang,Malaysia:IEEE,2013.249-255.

[2]Hammami O,Hamwi K.MHYNESYS II:multi-stage hybrid network on chip synthesis for next generation 3D IC manycore[A].Chang Wen Chen.IEEE International Symposium on Circuits and Systems (ISCAS)[C].Beijing:IEEE,2013.325-328.

[3]虞潇,李丽,张宇昂,等.一种面向功耗免死锁三维全动态3D NoC路由算法[J].电子学报,2013,41(2):329-334.

YU Xiao,LI Li,ZHANG Yu-ang,et al.A power-aware sead lock avoid three-dimensional full-adaptive routing algorithm for 3D NoC[J].Acta Electronica Sinica,2013,41(2):329-334.(in Chinese)

[4]Hamedani P K,Hessabi S,Sarbazi-Azad H,et al.Exploration oftemperature constraints for thermal aware mapping of 3D networks on chip[A].Rainer Stotzka.Proceedings of the 20th International Euromicro International Conference on Parallel,Distributed and Network-Based Processing (PDP 2012)[C].Garching,Germany:IEEE Computer Society,2012.499-506.

[5]Rahmani A M,Vaddina K R,Latif K,et al.Design and management of high-performance,reliable and thermal-aware 3D networks-on-chip[J].IET Circuits,Devices & Systems,2012,6(5):308-321.

[6]Wei Huang,Ghosh S,Velusamy S,et al.HotSpot:a compact thermal modeling methodology for early-stage VLSI design[J].IEEE Transactions on Very Large Scale Integration (VLSI) Systems,2006,14(5):501-513.

[7]Addo-Quaye C.Thermal-aware mapping and placement for 3-D NoC designs[A].Dong Ha.IEEE International SOC Conference[C].Herdon,Virginia,USA:IEEE,2005.25-28.

[8]闫佳琪,骆祖莹,唐亮,等.考虑温度对漏电流功耗影响的MPSoC结构级热分析方法[J].计算机辅助设计与图形学学报,2013,25(11):1767-1774.

Yan Jia-qi,Luo Zu-yin,Tang Liang,et al.High accurate architecture-leve thermal analysis methods for MPSoCs considering leakage power dependence on temperature[J].Journal of Computer-Aided Design & Computer Graphics,2013,25(11):1767-1774.(in Chinese)

[9]Bartolini A,Cacciari M,Tilli A,et al.Thermal and energy management of high-performance multicores:distributed and self-calibrating model-predictive controller[J].IEEE Transactions on Parallel and Distributed Systems,2013,24(1):170-183.

[10]Shuang Xie,Wai Tung Ng.Delay-line temperature sensors and VLSI thermal management demonstrated on a 60nm FPGA[A].Piotr Dudek.IEEE International Symposium on Circuits and Systems (ISCAS)[C].Melbourne VIC,Australia:IEEE,2014.2571-2574.

[11]Coskun A K,Rosing T S,Gross K C.Utilizing predictors for efficient thermal management in multiprocessor SoCs[J].IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems,2009,28(10):1503-1516.

[12]Zanini F,Atienza D,De Micheli G.A control theory approach for thermal balancing of MPSoC[A].Kazutoshi Wakabayashi.Proceedings of the 14th Asia and South Pacific Design Automation Conference[C].Yokohama,Japan:IEEE,2009.37-42.

[13]Xiaorui Wang,Kai Ma,Yefu Wang.Adaptive power control with online model estimation for chip multiprocessors[J].IEEE Transactions on Parallel and Distributed Systems,2011,22(10):1681-1696.

[14]Inchoon Yeo,Chih Chun Liu,Eun Jung Kim.Predictive dynamic thermal management for multicore systems[A].Limor Fix.Proceedings of the 45th Design Automation Conference[C].Anaheim,California,USA:ACM,2008.734-739.

[15]Bartolini A,Cacciari M,Tilli A,et al.A distributed and self-calibrating model-predictive controller for energy and thermal management of high-performance multicores[A].Kathy Preas.Proceedings of Design,Automation & Test in Europe Conference & Exhibition (DATE)[C].Grenoble,France:EDAA,2011.1-6.

[16]Dacheng Juan,Huapeng Zhou,Marculescu D,et al.A learning-based autoregressive model for fast transient thermal analysis of chip-multiprocessors[A].Kazutoshi Wakabayashi.Proceedings of the 17th Asia and South Pacific Design Automation Conference[C].Sydney,Australia:IEEE,2012.597-602.

[17]Kun-Chih Chen,Shu-Yen Lin,An-Yeu Wu.Design of thermal management unit with vertical throttling scheme for proactive thermal-aware 3D NoC systems[A].Ilderem V.Proceedings of the International Symposium on VLSI Design,Automation,and Test (VLSI-DAT)[C].Hsinchu:IEEE,2013.1-4.

[18]Shengquan Wang,Bettati R.Reactive speed control in temperature-constrained real-time systems[A].Stephanie Kawada.Proceedings of the 18th Euromicro Conference on Real-Time Systems[C].Dresden,Germany:IEEE Computer Society,2006.161-170.

[19]Skadron K,Stan M R,Wei Huang,et al.Temperature-aware microarchitecture[A].Bob Werner.Proceedings of the 30th Annual International Symposium on Computer Architecture[C].San Diego,California,USA:IEEE Computer Society,2003.2-13.

[20]Sungjun Im,Banerjee K.Full chip thermal analysis of planar (2-D) and vertically integrated (3-D) high performance ICs[A].Mark Law.2000 International Electron Devices Meeting[C].San Francisco,California,USA:IEEE,2000.727-730.

[21]Wei Huang,Allen-Ware M,Carter J B,et al.Temperature-aware architecture:lessons and opportunities[J].IEEE Micro,2011,31(3):82-86.

魏琳女,1990年10月出生于江苏省靖江市.2013年获得扬州大学广陵学院学士学位.现为扬州大学信息工程学院硕士研究生.主要研究方向为电子系统集成和专用集成电路设计.

E-mail:elitals@163.com

周磊(通信作者)男,1980年月出生于江苏省扬州市.2002年、2013年获得南京航空航天大学学士和博士学位.现为扬州大学信息工程学院讲师.主要研究方向为电子系统集成和专用集成电路设计.

E-mail:tomcat800607@126.com

A Predictive Thermal Model Combined with the Second Derivative for Multiprocessor System-on-Chips

WEI Lin1,ZHOU Lei1,WU Ning2,YANG Jing1

(1.CollegeofInformationEngineering,YangzhouUniversity,Yanghzou,Jiangsu225000,China;2.CollegeofElectronicandInformationEngineering,NanjingUniversityofAeronauticsandAstronautics,Nanjing,Jiangsu210016,China)

The regional temperature prediction is the basis of the efficient heat dissipation in multiprocessor system-on-chips (MPSoCs).Based on the thermal resistance and capacitance (Thermal RC) model,this paper proposed a predictive thermal model combined with the second derivative.It predicts the temperature accurately with low complexity,and increases the prediction time length within a certain prediction error range to reduce the number of times that the prediction module is invoked and the extra power consumption.Experimental results show that,compared to the existing model combined with the first derivative,the proposed model increases the prediction length by 1.6 times within the same acceptable prediction error range.When the prediction time length is increased to 2.5s,the prediction accuracy of the proposed model is 3.84% higher than that of the contrastive model.

multiprocessor system-on-chips (MPSoCs);thermal resistance and capacitance (Thermal RC) model;predictive thermal model

2014-11-20;修回日期:2015-01-28;责任编辑：覃怀银

国家自然科学基金(No.61376025，No.61301111);江苏省高校自然科学基金(No.13KJB510039);江苏省普通高校研究生科研实践计划项目(No.SJZZ-0182)

TN47

A

0372-2112 (2016)06-1272-07