采空区顶板流变破断发展及灾变时间

李　铁，刘诗杰，3，马海涛，张山林（1.北京科技大学 金属矿山高效开采与安全教育部重点实验室，北京 100083；2.北京科技大学 土木与环境工程学院，北京 100083；3.中国安全生产科学研究院，北京 100012；4.矿山采空区灾害防治国家安全生产监督管理总局 安全生产重点实验室，北京 100012）

采空区顶板流变破断发展及灾变时间

李铁1，2，刘诗杰1，2，3，马海涛3，4，张山林1，2
（1.北京科技大学 金属矿山高效开采与安全教育部重点实验室，北京 100083；2.北京科技大学 土木与环境工程学院，北京 100083；3.中国安全生产科学研究院，北京 100012；4.矿山采空区灾害防治国家安全生产监督管理总局 安全生产重点实验室，北京 100012）

采用广义Kelvin体建立采空区顶板-矿柱流变体系，基于弹性力学理论进行体系沉降与时间对应关系的求解，并带入实际案例进行验证。结果表明：顶板沉降发展总体符合广义Kelvin体描述的阶段性沉降特性，但由于实际边界条件的改变为一渐变过程，顶板沉降可表现为多阶段变化，甚至连续变化。尽管顶板实际沉降变化受过程影响与理论计算有所差别，但建立的基于广义Kelvin体的采空区流变模型对采空区稳定时间预测较为可信，可应用于矿山稳定性评估及合理采取安全措施。

采空区；流变性能；广义Kelvin体本构模型；顶板沉降

岩石材料的流变指岩石的应力、应变随时间逐渐改变的性质。对于空场法采矿形成的采空区，顶板暴露面积大，空区存在时间长，岩石的流变对空区顶板的稳定性影响巨大［1］。过往针对采空区稳定性及安全分析［2］的研究较多，不同理论被应用于采空区简化模型处理及顶板-矿柱体系的应力应变研究，但多限于临界条件与失稳机理等，如顶板极限跨距研究［3］和不同开采形式下岩体应力分布规律［4］等，针对岩体流变特性的研究较少。

近年来，国内外学者逐渐意识到本构模型及其决定的瞬时、流变特性对于岩体及地下工程研究具有重要意义［5-6］，并针对这一性质进行了深入的研究。张龙云等［7］通过实验室手段对硬脆性辉绿岩的流变破坏过程进行了研究，得到了多种加载方式下不同种类的分级曲线，对揭示岩体流变特性具有重要意义。YU等［8］对软岩地质环境中隧道围岩变形圈进行研究，采用数值模拟方法，并结合相关弹性力学理论，所得结论具有一定的科学性与指导意义；杨振伟等［9］通过对Burgers体各元件参数的控制变量分析，深入研究了各元件对Burgers体性质的影响，进一步解析了Burgers体反映岩体性质的机制；孙琦等［10］和于跟波等［11］通过引入Burgers体作为岩体本构模型，对矿柱-顶板流变体系进行解析计算，在未完全求解条件下揭示了空区变化的特点。李大钟［12］深入解析采空区Kelvin体下的顶板控制方程，在Kelvin体未考虑岩体初始弹性变形条件下得到空区变形随时间发展的关系。

已有研究者在空场法采矿岩石流变对空区顶板稳定性方面的研究在理论和工程应用方面发挥了重要作用。限于科技发展的水平，过往关于采空区岩体流变特性及本构模型［13］的研究主要存在以下两方面缺憾：

1）缺乏合理的简化模型模拟空区中顶板-矿柱体系，并通过有效的数学方法求解得到具有代表性、普适性的空区流变方程；

2）研究方法多为实验室物理试验及数值模拟，采空区实测数据检验不足，偏于基础理论研究。

本文作者采用广义Kelvin体建立采空区顶板-矿柱流变体系，基于弹性力学理论进行体系沉降与时间对应关系求解，并带入实际案例进行验证。

1　广义Kelvin本构模型简介

Burgers体对于岩体性质反映较为全面［14］，但不利于计算求解，Kelvin体结构简单，但不能综合反映岩体性质。广义Kelvin体既能较为全面地反映岩体性质，又能兼顾计算需求，可应用于采空区流变失稳的研究中。

广义Kelvin体由由一个弹性元件与Kelvin体串联而成，其本构模型与蠕变曲线如图1所示。

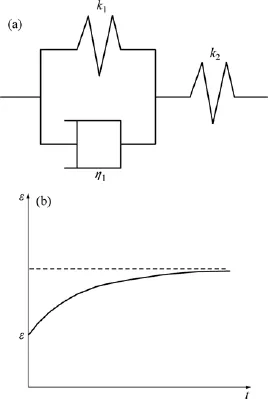
图1　广义Kelvin体本构模型及蠕变曲线Fig.1　Constitutive model and creeping curve of generalized Kelvin model

广义Kelvin体的本构方程为

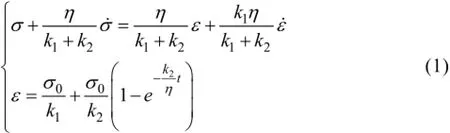
2　顶板流变沉降过程分析

将矿柱视为性质相同的广义Kelvin体，建立简化的空区模型，模型中弹簧元件弹性系数分别为k1，k2，阻尼器阻尼为η，如图2所示。

假设顶板承受上覆岩层均布荷载完全由矿柱传递，矿柱端部的变形即为顶板对应处的沉降量，因而矿柱端部变形量对顶板形变、应力分布具有重要意义，矿柱的大变形最终引起顶板拉破坏，最终形成坍塌失稳。矿柱端部变形与单元应变关系

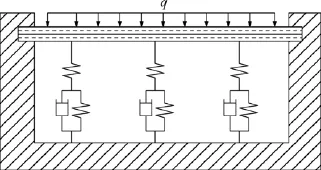
图2 采空区简化模型Fig.2　Simplified model of goaf

式中：H为矿柱高度，m。

顶板控制方程：

为泊松比；ζ为将矿柱应力等效成均布应力系数。

将广义Kelvin体本构方程（1）与应力应变关系式（2）代入顶板控制方程中，消去矿柱应力，得

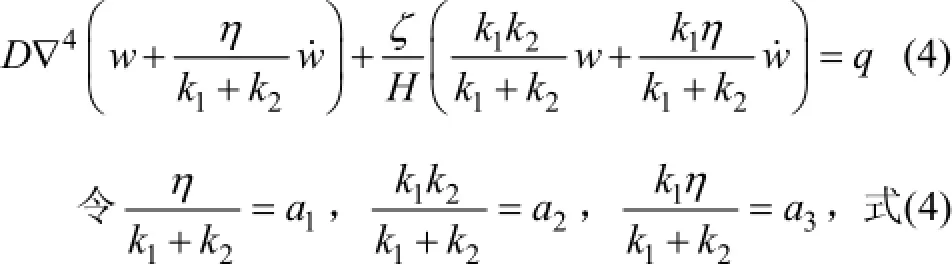
可写为

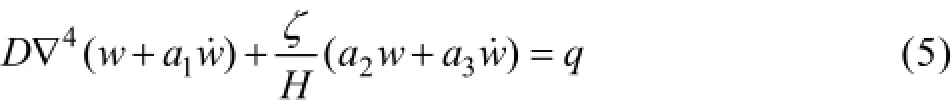
在顶板中建立坐标系如图3所示。

假设顶板的沉降变形分布可表示为

式中：w0（t）为顶板中心最大挠度； （，）x yφ为描述顶板沉降分布的形函数。

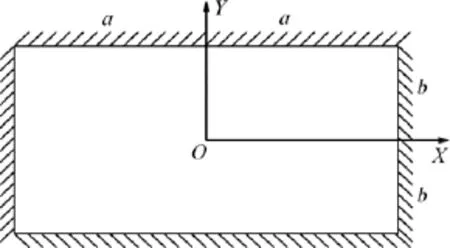
图3 顶板内坐标系Fig.3　Coordination in roof

将式（6）代入式（5），式（6）的Galerkin形式为：

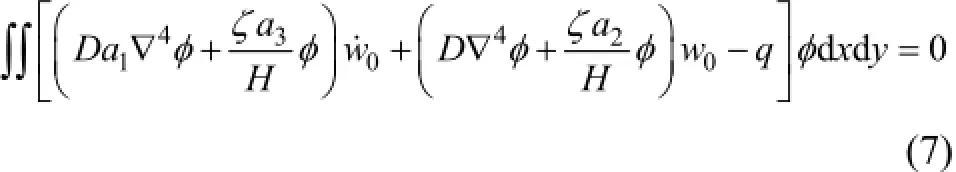
令

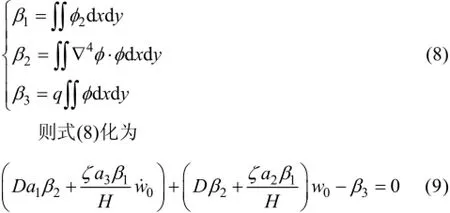
此时，顶板控制方程转化为常微分方程形式

式中：

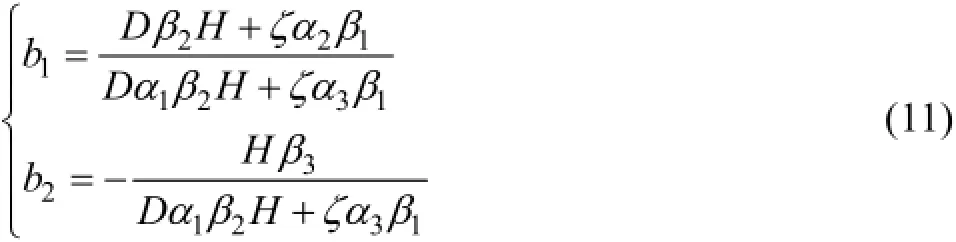
求解此常微分方程得

3　顶板破断条件分析

仍参考图3中所示的顶板内坐标系，顶板沉降变形根据其边界条件的不同被分为3个阶段。第一阶段，顶板四周固支，此阶段顶板变形将引起长边边界破坏。边界条件为

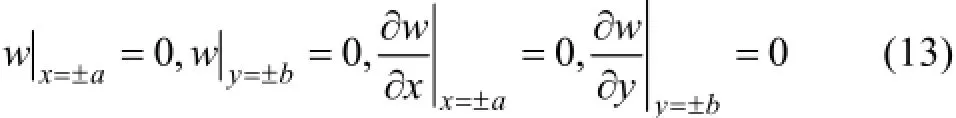
使用弹性力学半逆解法对该顶板沉降分布函数进行求解。沉降分布函数应满足：1）顶板相容方程

40Φ

∇=；2）应力边界条件；3）位移单值条件；4）求解对象特定边界条件。王金安等［14］对顶板变形的研究表明，顶板沉降分布的形函数可表示为

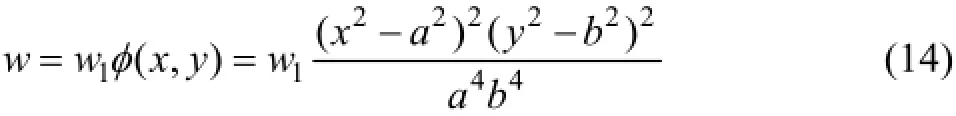
顶板破断的类型，根据受力机理的不同主要分为以下3类：1）拉应力引起的拉张破坏；2）剪应力引起的剪切破坏；3）矿柱失稳引起的垮冒破坏。本研究中，矿柱被视为墩型，不考虑失稳破坏；顶板为薄板，破断形式主要受拉应力控制。根据弹性力学理论，长边破坏时顶板内部沉降极限w1（t）应满足

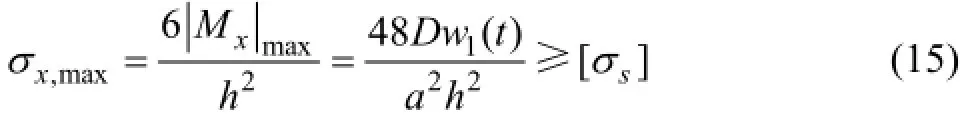
式中：［σs］为岩体抗拉强度。

第二阶段，顶板长边发生破坏，约束状态为铰支，但短边仍为固支边界，此阶段顶板变形将引起短边发生边界破坏，进而进入内部破坏阶段。边界条件

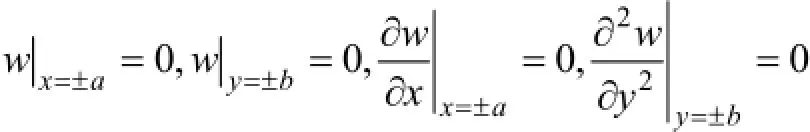
顶板沉降分布的形函数为

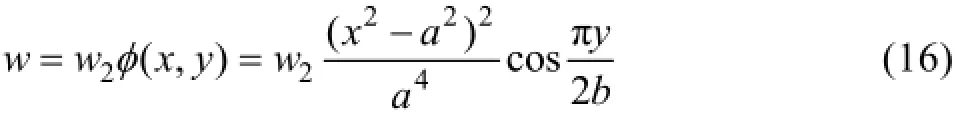
短边破断时顶板内部沉降极限w2（t）满足

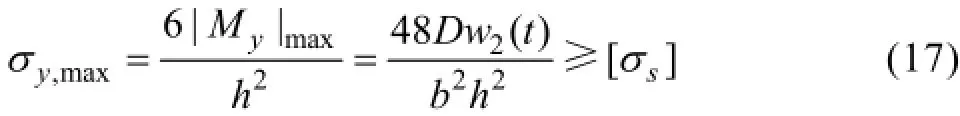
第三阶段，顶板四周边界破坏，由固支变成铰支，顶板的进一步变形将造成顶板中心呈“X”形破坏。边界条件为

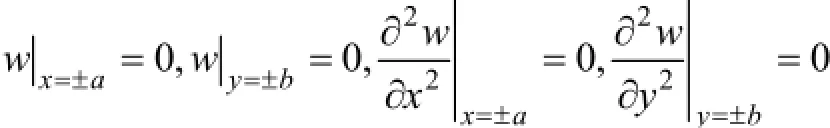
顶板变形分布形函数为

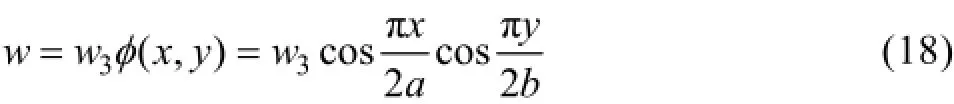
内部破坏时顶板最大沉降w3满足

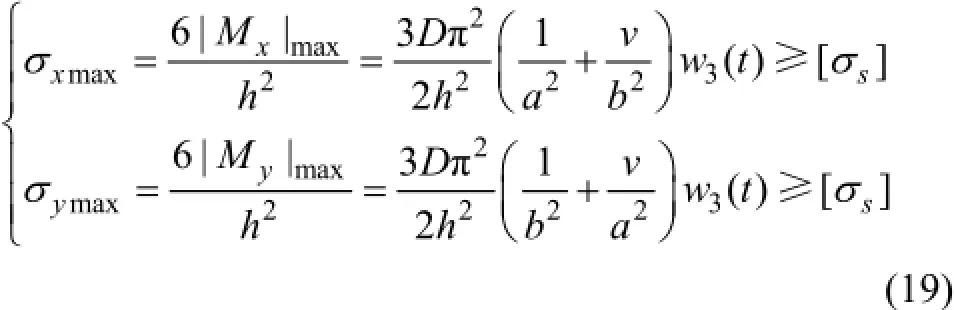
3个阶段顶板变化如图4所示。

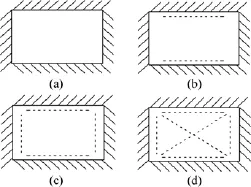
图4　顶板变形破坏过程Fig.4　Process of roof subsiding and failing：（a）Four sides hinged roof；（b）Long sides failed，short sides hinged；（c）Four sides failed；（d）Inside failure in roof

4　顶板破断发展及时间分析

上述计算表明，顶板沉降的发展具有连续性与突变型，边界条件的改变将引起沉降分布函数 （，）x yφ的改变，导致各阶段对应的式（7）中的积分常数与顶板控制方程通解中相关参数（b1，b2）各不相同，从而引起不同阶段顶板变形曲线的变化。

式（11）中，顶板变形方程的通解中包含一未知参数c，该参数由各阶段的初始条件求得，即

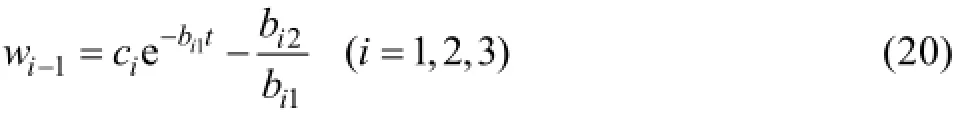
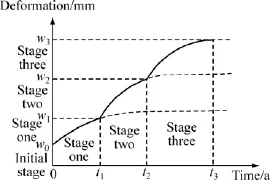
图5　顶板沉降曲线Fig.5　Curve of roof subsiding

根据顶板沉降曲线与式（14）～（18）中的破断极限条件，即可分别计算出顶板流变发展经历各阶段所用时间ti（i=1，2，3），空区稳定时间即为3个阶段历时之和t=t1+t2+t3。

5　流变破断理论实用研究

5.1空区失稳时间验证分析

河北省邢台县尚旺庄石膏矿建于1984～1998年，分康立、林旺、太行、邢燕、第二石膏矿共5座矿（见图6）。矿区地表下第四系覆岩厚为145 m，顶板为灰岩，厚度h=38 m，各地层性质如表1所列。该矿于2005年11月6日发生特别重大坍塌事故，发生坍塌的采空区近似矩形区域，坚硬顶板长度为2a=280 m，宽度2b=180 m。空区矿柱群均布力系数ζ=39.16%，矿柱高度H=8 m，矿柱流变参数η=6.41×108MPa·h。

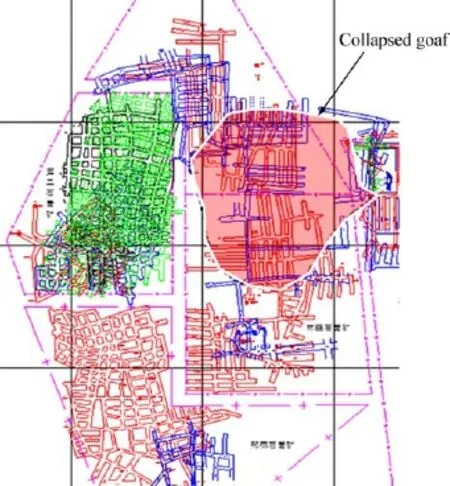
图6 灾变空区示意图Fig.6　Picture of collapsed goaf

运用基于广义Kelvin体的矿柱顶板流变失稳体系进行计算。矿柱弹性系数

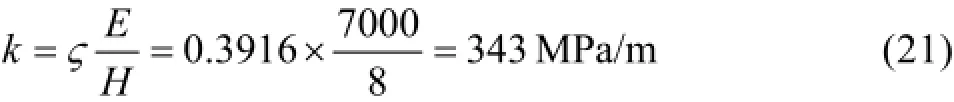
广义Kelvin体中两弹簧元件的弹性系数分别为k1=3811 MPa/m，k2=381 MPa/m

计算结果如表2所列。

经计算，该矿采空区稳定时间t=t1+t2+t3=15.93 a，自1984年建矿之后采空区开始形成至2005年发生灾变，实际自稳时间t≤21 a，考虑建矿之初顶板暴露面积小，流变效果不明显，本文作者对空区稳定时间的预测基本符合实际情况。

5.2顶板变形发展趋势应用

江西某钨矿曾于1966年6月和1967年7月在矿区上部发生了破坏性地压活动，自1998年至今，采掘作业转入深部范围后，矿区地压活动局部—区域表现尤为剧烈，严重威胁485 m至335 m中段工程岩体稳定性。为了保证生产作业安全与稳定，从2012年起，使用数显收敛监测仪对该区域顶板及围岩沉降、变形量进行了为期数年的监测记录，如图7所示。

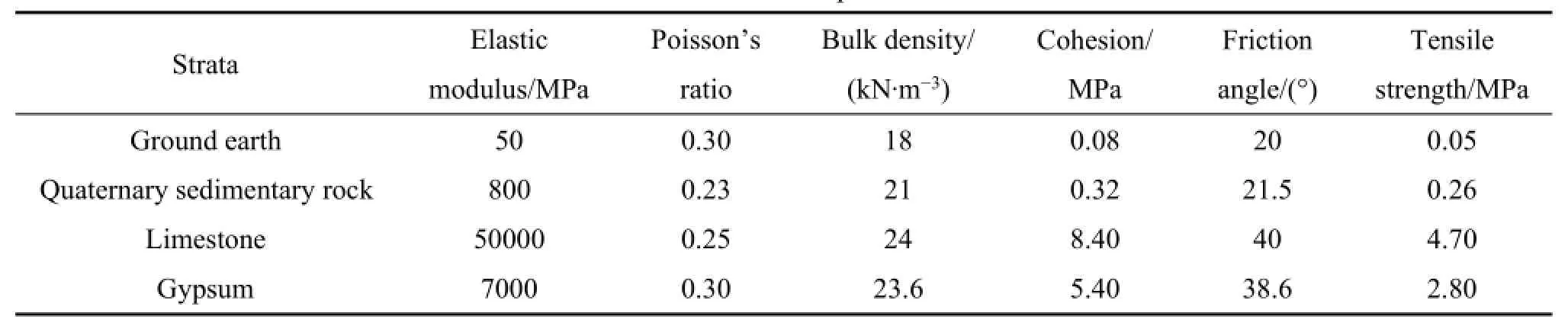
表1　矿区主要岩石力学参数Table 1　Main mechanical parameters of rock

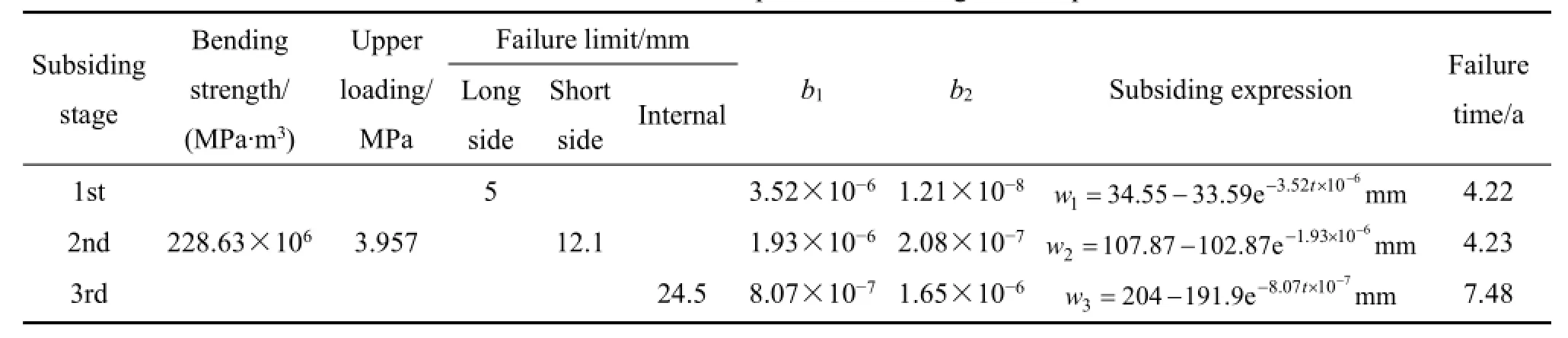
表2　矿柱顶板流变失稳计算Table 2　Calculation of pillar-roof rheological collapse

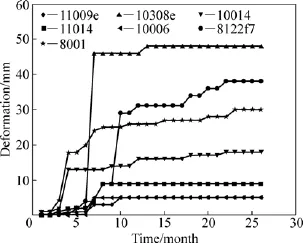
图7　部分监测点变形走势Fig.7　Deformation developing of some points

通过以上7组监测点走势图可以看到，空区围岩的变形具有如前文研究得出的“收敛-发散-收敛”往复式发展，在监测初期（0～5月），沉降变形较小，各监测点测得数据均基本保持稳定；监测第5～10月期间，各组监测数据均出现了不同程度的突变发育，其中10308e监测点在1个月内变形量增大约50 mm。后各组数据又趋于稳定至第26月，没有发生突变发育。

基于上述各监测数据的变化形式，可得出结论：

1）485～335 m中段围岩并非完全稳定，监测数据的突变发育表明顶板短边发生过破坏，部分区域进入第二阶段，即长边破坏阶段；

2）就目前而言，该区域围岩变形稳定，无大规模冒落危险性，但对顶板围岩的监测工作不应停止，一旦顶板进入内部破坏阶段，系统受力机理将出现改变，空区将可能出现失稳危险。

同时，由于顶板边界条件的变化并非瞬时完成，而是一逐渐失稳的过程，部分监测点沉降走势并不呈现出明显的收敛特性，而是趋向于Burgers体描述的“稳定蠕变”特性，如图8所示。

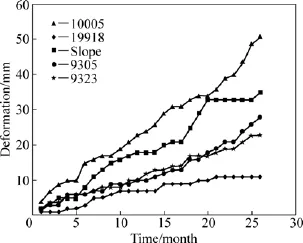
图8　变形稳定发展监测点Fig.8　Deformation developing steadily points

6　结论

1）针对采空区流变失稳的计算对于矿山安全生产具有较高的指导意义，具体区域的围岩变形发育过程可能因差异化的岩体构造、地层结构等有所偏差，但对空区整体稳定时间的计算结果基本符合实际。

2）围岩监测工作应密切关注变形量突增事件，某一区域围岩变形量在短时间内大量增长可能表明该区域岩体整体稳定性构造出现了破坏与变化，需采取应急措施进行排查、治理。

3）广义Kelvin体空区模型的计算并未考虑地下水、节理、风化作用等外界因素的影响，如要对此类因素影响顶板失稳机理的研究，可对相关参数进行折减。

REFERENCES

［1］ MAHai-tao，WANGJin-an，WANGYun-hai.Studyon mechanics and domino effect of large-scale goaf cave-in［J］. Safety Science，2012，（S50）：689-694.

［2］ 习心宏，冯夏庭，于培言，蔡鸿起.空场采矿法采场顶板破坏模式识别专家系统［J］.中国有色金属学报，2001，11（1）：157-161. XI Xin-hong，FENG Xia-ting，YU Pei-yan，CAI Hong-qi.Expert systeminidentifyingfailuremodeofhangingwallof room-and-pillar mining［J］.The Chinese Journal of Nonferrous Metals，2001，11（1）：157-161.

［3］ 史红，姜福兴.采场上覆大厚度坚硬岩层破断规律的力学分析［J］.岩石力学与工程学报，2004，23（18）：3066-3069. SHI Hong，JIANG Fu-xing.Mechanical analysis of rupture regularity of hard and massive overlying strata of longwall face［J］.Chinese Journal of Rock Mechanics and Engineering，2004，23（18）：3066-3069.

［4］ HU Jian-hua，LEI Tao，ZHOU Ke-pin，LUO Xian-wei，YANG Nian-ge.Mechanical response of roof rock mass unloading during continuous mining process in underground mine［J］. Transactions of Nonferrous Metals Society of China，2011，21（12）：2727-2733.

［5］ CAO Ping，WAN Lin-hui，WANG Yi-xian，HUANG Yong-heng，ZHANG Xiang-yang.Viscoelasto-plastic properties of deep hard rocks under water environment［J］.Transactions of Nonferrous Metals Society of China，2011，21（12）：2711-2718.

［6］蒋斌松，蔡美峰，贺永年，韩立军.深部岩体非线性Kelvin蠕变变形的混沌行为［J］.岩石力学与工程学报，2006，25（9）：1862-1867. JIANG Bin-song，CAI Mei-feng，HE Yong-nian，HAN Li-jun. Chaotic behavior of nonlinear Kelvin creep of rock mass in deep ground［J］.Chinese Journal of Rock Mechanics and Engineering，2006，25（9）：1862-1867.

［7］ 张龙云，张强勇，杨尚阳，隋斌，杨文东，王有法，王超，袁圣渤.大岗山坝区辉绿岩卸围压三轴流变试验及分析［J］.中南大学学报（自然科学版），2015，46（3）：1034-1042. ZHANG Long-yun，ZHANG Yong-qiang，YANG Shang-yang，SUI Bin，YANG Wen-dong，WANG You-fa，WANG Chao，YUAN Sheng-bo.Analysis of unloading confining pressure triaxial rheological tests of diabase in Dagangshan dam side［J］. Journal of Central South University（Science and Technology），2015，46（3）：1034-1042.

［8］ YU Yang，ZHU Cai-kun，CHONG De-yu，LIU Yang，LI Si-chao. Catastrophe mechanism and disaster countermeasure for soft rock roadway surrounding rock in Meihe mine［J］.International Journal of Mining Science and Technology，2015（25）：407-413.

［9］ 杨振伟，金爱兵，周喻，严琼，王凯，高玉娟.伯格斯模型参数调试与岩石蠕变特性颗粒流分析［J］.岩土力学，2015，36（1）：240-248. YANG Zhen-wei，JIN Ai-bing，ZHOU Yu，YAN Qiong，WANG Kai，GAO Yu-juan.Parametric analysis of Burgers model and creep properties of rock with particle flow code［J］.Rock and Soil Mechanics，2015，36（1）：240-248.

［10］孙琦，魏晓刚，卫星，杨逾，杨佳，邢洋.采空区矿柱流变特性对露天矿边坡稳定性的影响研究［J］.中国安全科学学报，2014（8）：85-91. SUN Qi，WEI Xiao-gang，WEI Xing，YANG Yu，YANG Jia，XING Yang.Study on effects of pillars rheological properties on open-pit slope stability［J］.China Safety Science Journal，2014（8）：85-91.

［11］于跟波，杨鹏，陈赞成.缓倾斜薄矿体矿柱回采采场围岩稳定性研究［J］.煤炭学报，2013（S2）：294-298. YUGen-bo，YANGPeng，CHENZan-cheng.Studyon surrounding rock stability of pillar extraction in thin gently inclined ore body［J］.Journal of China Coal Society，2013（S2）：294-298.

［12］李大钟.空场法采空区稳定性及安全评价研究［D］.北京：北京科技大学，2009. LI Da-zhong.Study on the stability of mined-out goaf and its safetyevaluation［D］.Beijing：UniversityofScienceand Technology Beijing，2009.

［13］陈阮江，潘长良，曹平，王文星.基于内时理论的软岩流变本构模型［J］.中国有色金属学报，2003，13（3）：735-742. CHEN Yuan-jiang，PAN Chang-liang，CAO Ping，WANG Wen-xing.Endochronic rheological constitutive model of soft rock［J］.The Chinese Journal of Nonferrous Metals，2003，13（3）：735-742.

［14］王金安，李大钟，马海涛.采空区矿柱-顶板体系流变力学模型研究［J］.岩石力学与工程学报，2010，29（3）：577-582. WANG Jin-an，LI Da-zhong，MA Hai-tao.Study of rheological mechanical model of pillar-roof system in mined-out area［J］. Chinese Journal of Rock Mechanics and Engineering，2010，29（3）：577-582.

［15］ZHOU Jian，LI Xi-bing，SHI Xiu-zhi，WEI Wei，WU Bang-biao. Predicting pillar stability for underground mine using Fisher discriminant analysis and SVM methods［J］.Transactions of Nonferrous Metals Society of China，2011，21（12）：2734-2743.

(编辑王超)

Development and catastrophe time of rheological collapse in goaf roof

LI Tie1，2，LIU Shi-jie1，2，3，MAHai-tao3，4，ZHANG Shan-lin1，2
（1.State Key Laboratory of High-efficiency Mining and Safety of Metal Mines，Ministry of Education，University of Science and Technology Beijing，Beijing 100083，China；2.School of Civil and Environment Engineering，University of Science and Technology Beijing，Beijing 100083，China；3.ChinaAcademy of Safety Science and Technology，Beijing 100012，China；4.Key Laboratory on Mining Goaf Disaster Prevention，State Administration of Work Safety，Beijing 100012，China）

A roof-pillars rheological system of goaf was built based on the elastic theory and generalized Kelvin constitutive model，and the function relationship between subsiding and time was solved out.Solutions were tested in actual cases.The results show that，although the development of roof subsiding matches well with the periodical characteristics described by the generalized Kelvin model，the roof subsiding can change multiperiodically or even constantly due to the fact that the changing of the actual boundary condition is a gradual process.Although there are some differences between the actual roof subsiding process and theoretical solutions because of the procedural effect，the result on the goaf stable time in generalized Kelvin goaf rheological model is still credible.The conclusions can be applied mines stability evaluation and taking the safety measures reasonably.

goaf；rheological property；generalized Kelvin constitutive model；roof subsiding

Project（51274025）supported by the National Natural Science Foundation of China

date:2015-05-06；Accepted date:2015-11-10

LI Tie；Tel：+86-15810786767；E-mail：litie@ustb.edu.cn

TG142.71

A

1004-0609（2016）-03-0666-07

国家自然科学基金资助项目（51274025）

2015-05-06；

2015-11-10

李铁，教授，博士；电话：15810786767；E-mail：litie@ustb.edu.cn