Lorenz混沌同步系统虚拟仪器网络化实现*
2016-08-11谢永兴胡云安
谢永兴 胡云安 林 涛 秦 亮
(1.海军航空工程学院控制工程系 烟台 264001)(2.海军航空工程学院科研部 烟台 264001)
Lorenz混沌同步系统虚拟仪器网络化实现*
谢永兴1胡云安1林涛2秦亮1
(1.海军航空工程学院控制工程系烟台264001)(2.海军航空工程学院科研部烟台264001)
摘要研究了Lorenz系统同步原理,并在LabVIEW中实现四阶Runge-Kutta算法仿真。比较和总结了LabVIEW中多种网络通信方式的应用场合和优缺点,并选用基于DataSocket的网络通信方法实现主机端和客户端VI设计。VI界面友好、操作简单。经过Matlab仿真发现两者的结果高度一致,说明LabVIEW不仅具备优秀的图形图像处理能力,还具备强大的信号数据处理功能。
关键词Lorenz系统; 混沌同步; LabVIEW; Runge-Kutta; DataSocket网络通信
Class NumberO415.5
1 引言
1963年气象学家E. N. Lorenz在研究大气热对流时发现了一种特殊的现象,即著名的蝴蝶效应[1]。经研究发现,某些确定性系统对初值特别敏感,初值稍有变化,经长时间演化后系统状态将截然不同,这就是所谓的混沌。混沌学在科学界享有很高的评价,被称为物理学发生的第三次革命,它与相对论、量子力学同被列为20世纪的最伟大发现之一。目前,混沌理论与其它学科相互渗透,在图像、视频、语音等信号加密中应用广泛[2~4],混沌同步在保密通信方面的应用则是近几十年来研究的热点。
混沌保密通信和混沌同步电路的研究是紧密相关的。Chua构造了一种结构非常简单但是动力学行为非常丰富的非自治混沌电路,成为混沌电路研究的范例[5]。Carroll和Pecora研究了Newcomb电路的混沌同步现象,证明了被同一信号联结的某些混沌系统能够实现稳定同步[6]。Cuomo等研究了Lorenz系统电路混沌同步,并将其应用在通信中[7],证实了混沌同步过程具有一定的鲁棒性,能在连续摄动的作用下保持稳定。
LabVIEW是虚拟仪器开发的引领者,是未来开发测试软件的总体趋势。LabVIEW使用模块化的图形函数,只需简单地拖动图标和连线即可实现编程,其特有的加亮执行功能使调试变得异常容易,利用LabVIEW相关工具包还能进行数据库的连接、控制设计与仿真、运动检测等功能。LabVIEW兼备各种优点,使其在测试和仿真领域得到广泛应用[8~9]。而将网络技术和虚拟仪器相结合,不仅可以完成信号处理、图形显示等功能,还摆脱了地域上的限制,实现测试或仿真过程的远程控制。
本文首先研究了Lorenz系统混沌同步原理,然后介绍了LabVIEW中多种网络通信方式。在LabVIEW中通过四阶Runge-Kutta算法求解Lorenz混沌同步系统,并选用基于DataSocket的网络通信方法实现对虚拟仪器VI的远程控制。
2 Lorenz系统同步原理
Lorenz系统[1]表示为

(1)
其中σ、r和b为参数。Pecora和Carroll已经证明Lorenz系统可分解为两个稳定子系统。特别地,稳定响应子系统(x1,z1)可定义为
(2)
另一个稳定响应子系统(y2,z2)定义为
(3)
式(1)的动力学行为不依赖响应子系统,可视为驱动系统。式(2)和(3)分别表示由驱动信号y(t)和x(t)驱动的动力响应系统。(x1,z1)子系统Jacobian矩阵特征值都为负值,表明当t→∞时|x1-x|及|z1-z|→0。还能通过数值方法证明(y2,z2)子系统的Lyapunov指数都为负,因此,当t→∞时有|y2-y|及|z2-z|→0。
两个响应子系统也可以一同使用,复现出驱动系统演化的全维动力学。特别地,如果(y2,z2)子系统输入是x(t),则其输出y2(t)可用来驱动(x1,z1)子系统,并产生一个新的x(t),加上通过同步获得的y(t)和z(t)。两个响应子系统可以合成一个具有三维状态空间的系统,产生的全维响应系统在结构上与驱动系统(1)类似。
3 LabVIEW网络通信
在LabVIEW中有多种方法实现网络通信,归纳起来主要分为以下四种: 1) TCP与UDP通信; 2) DataSocket技术; 3) 共享变量; 4) 远程VI面板连接。
3.1TCP与UDP通信
TCP/IP是一个由不同层次上的多个协议组合而成的协议族,包括网络接口层、Internet层、传输层和应用层[10]。TCP和UDP是TCP/IP协议族中使用最广泛、最重要的传输层协议,都使用IP作为网络层协议。
TCP通信方式在通信前必须在服务器和客户端之间先建立起可靠连接,因此能够保证数据的无差错传输。其通信过程为:在服务器端指定主机名或IP地址、端口号,通过侦听函数建立侦听,然后等待客户端建立连接。客户端发出连接请求,注意请求时配置的主机名或IP地址、端口号必须与服务器端配置相同。连接成功后,通过读写函数完成TCP数据通信。
与TCP相比,UDP采用广播方式进行通信,通信前无需建立可靠连接,因而会有一定量的数据丢失。但是UDP响应速度快,对于某些有实时需求但对数据传输要求不高的应用程序来说更为便利。
TCP与UDP通信方式从编程流程上看较为复杂,但是考虑到大部分计算机都支持这两种协议,在一些特定场合它们仍然是唯一的选择,如实现与C语言所编写程序之间的通信。
3.2DataSocket
DataSocket技术建立在TCP/IP基础之上,是一种专为测控领域设计的网络编程技术,其数据交换具有较好的实时性[11]。通过屏蔽各种网络通信细节,使整个编程过程大大简化。DataSocket不仅支持包括FTP、OPC、HTTP等Windows标准协议,而且专门开发了FILE、PSP、DSTP等LabVIEW专用协议,用以提高通信的可靠性。网络通信中,使用统一资源标识符(Uniform Resource Locator,URL)标识网络资源的地址,并根据不同的通信协议采取不同的格式。
DataSocket网络通信包括DataSocket服务器和DataSocket API,其中DataSocket服务器主要负责底层通信的所有细节,DataSocket API则负责URL所连接资源的打开、读写及关闭操作[12]。
使用DataSocket实现通信时必须先运行服务器,其具体位置为“开始|程序|National Instruments|Datasocket|DataSocket Server”。位于相同位置的DataSocket Server Manager可完成对服务器参数的配置、预定义数据项目的创建及配置等。启动DataSocket服务器后,将自动创建预定义数据项目。事实上,在实际编程过程中,并不需要将所有要使用的数据项目都预先定义,打开或读写操作时会自动创建,极大地简化了编程。
DataSocket通信分无缓冲和有缓冲两种方式。无缓冲方式在读写DataSocket时会自动打开数据连接,不必另外使用打开DataSocket函数。值得注意的是,读取DataSocket函数的“等待更新值”输入端为真时,数据项目更新后立即返回更新值,类似于中断式事件触发;输入端为假时,返回的是当前值,此时如果数据读取速度低于数据发布速度,将存在数据漏读。有缓冲方式通过缓冲机制,能够解决读取速度偶尔偏慢造成的数据丢失问题。
3.3共享变量
共享变量是出现于DataSocket之后的一种网络通信方式,通过特殊的内部缓冲机制,有效避免了全局变量的数据竞争问题。共享变量的读写操作可通过DataSocket函数实现,而创建和发布共享变量则需要LabVIEW实时模块的额外支持。共享变量支持包含I/O点在内的所有LabVIEW数据类型,使网络数据如本地数据一样便于获取。共享变量引擎使用PSP协议,完成对共享变量使用、连接的发布及管理。共享变量采用的网络地址格式为:psp://计算机名/项目库名/变量名。
创建共享变量前需要在项目中新建项目库,然后通过项目库的快捷菜单新建变量。变量的类型必须设置为网络发布型,才能使网络上其它节点访问该变量。共享变量可以绑定到项目中或网络上已有的共享变量上,也可以通过控件属性对话框中的“数据绑定”选项卡和控件建立连接。执行调用共享变量VI前应手动或自动布署共享变量。
3.4远程VI面板连接
诸如实际工程应用中的监控类程序,绝大多数时间仅需要浏览远程计算机上的VI前面板,而操作量相对较少,此时可通过Web服务器技术实现此功能。其实现过程非常简单,首先需要在服务器端配置并启动LabVIEW Web服务器,然后在客户端通过网页或LabVIEW Run-Time引擎两种方式连接远程面板[13]。远程VI面板连接过程中,也是使用URL进行网络资源定位的,如使用网页方式浏览远程VI时,在浏览器地址栏填写的就是之前配置服务器时填入的VI URL地址。
4 LabVIEW虚拟仪器设计
虚拟仪器实现主要包括两个VI的设计:实现Lorenz系统的主机端VI和接收Lorenz系统变量网络数据的客户端VI。下面分别介绍其具体设计细节。
4.1主机端VI
考虑由x作为驱动信号的驱动响应系统,结合式(1)和式(3)组成一个五维方程组:
(4)
其中σ=10,r=28,b=8/3,初值(x,y,z,y2,z2)t=0=(1,1,1,3,2),仿真区间为[0,100],步长h=0.01。
在程序框图中,通过选取函数选板中的“数学|微分方程|常微分方程”中的“ODE库塔四阶方法”函数实现式(4)的求解。必须设置好该函数的常微分方程的右侧、变量、起始时间、终止时间、步长等参数,才能保证运行后输出正确的时间及解数据。注意,输出的时间为一维数组,解为二维数组,一列对应一个变量,行数取决于Runge-Kutta算法的迭代次数。通常需要对解数据进行转置,以便于信号的处理和显示。
通过“索引数组”函数分离五个变量,前三个对应驱动系统变量,后两个对应响应系统变量。在前面板添加位于“新式|图形|三维图形”的“三维线条图形”控件,并切换至程序框图中将刚提取出的驱动系统的3个变量依次连接到其输入端,完成驱动系统3D相图的显示。
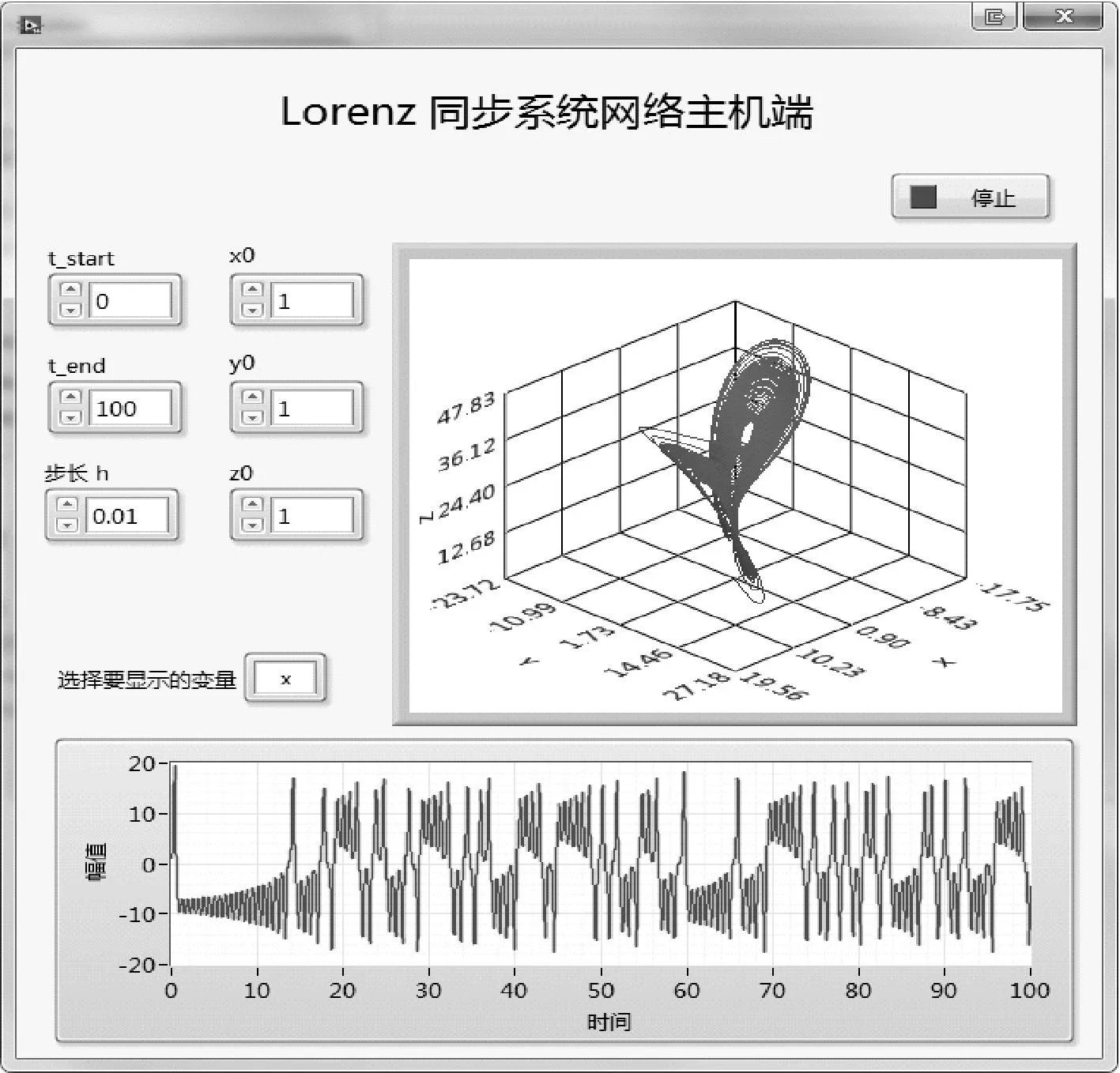
图1 主机端VI前面板
图3所示为实现网络通信时用到的两个核心函数,分别完成DataSocket的读取和写入。“连接输入”接线端所接数据类型为字符串类型,用于指定要读取的数据源或要写入的数据终端,其格式为:dstp://主机名称/变量名,如主机端VI中的dstp://localhost/datat。值得注意的是,本文设计的主机端VI和客户端VI位于同一台计算机上,所以主机名称是localhost;如果是两台计算机进行通信,此处应用主机计算机的IP地址替换。程序框图中用了5个写入DataSocket函数,使x,y,z,y2,z2等变量可通过网络进行访问;还用了2个读取DataSocket,用于从客户端VI读取对响应子系统变量初值的设置。
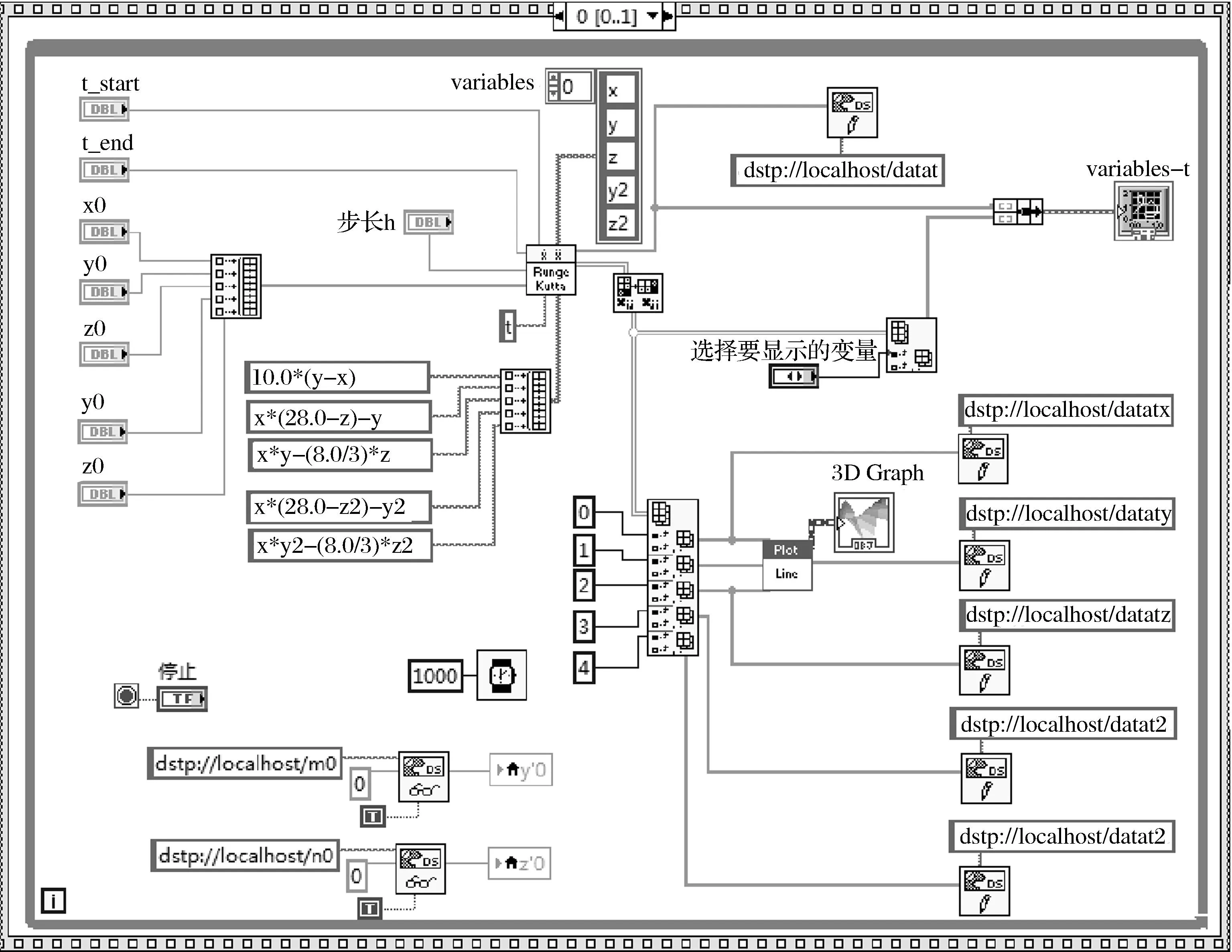
图2 主机端VI程序框图
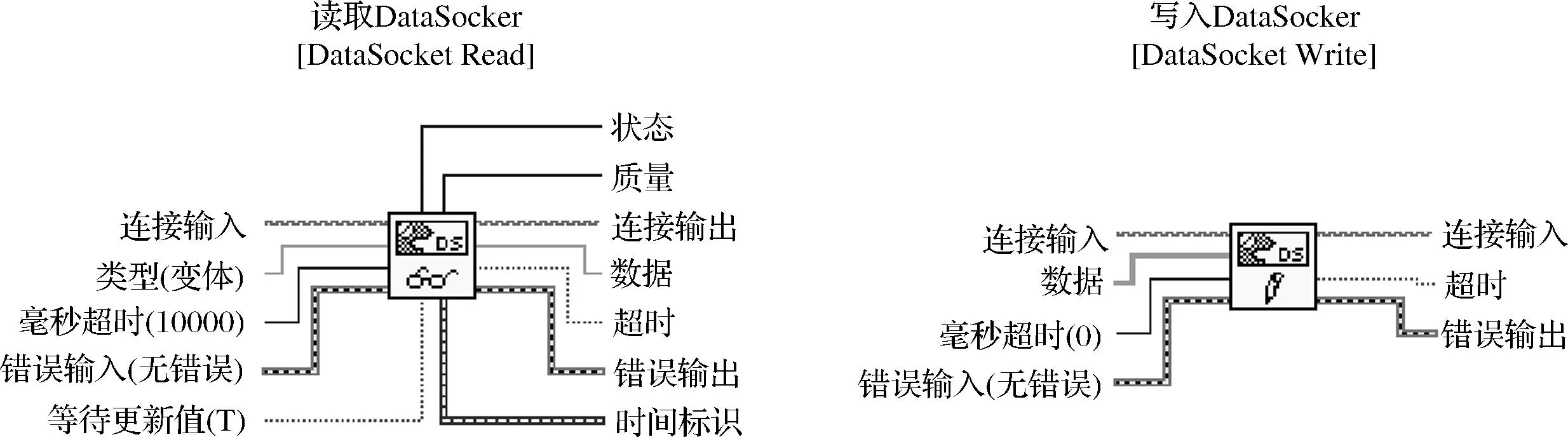
图3 读取与写入DataSocket函数
合理地编辑前面板上“选择要显示的变量”枚举控件,使枚举项的值对应变量在数组中的行索引值,从而控制对应的变量显示于XY图中,图1中选择显示的变量是x。
程序的主体部分放置在一个While循环内,改变初值的设置,将自动重新进行计算,绘制更新后的信号曲线。
4.2客户端VI
客户端VI的前面板和程序框图分别如图4、图5所示。与主机端VI相对应,在程序框图中主要使用了五个读取DataSocket函数,获取Lorenz驱动响应系统的变量数据;另外利用两个数值控件及两个写入DataSocket函数,用于控制主机端VI中响应子系统初值。前面板中XY图显示了驱动系统和响应系统y,z两个分量的误差曲线,由图可以看出,响应系统与驱动系统之间的误差很快便收敛到零,即达到同步。

图4 客户端VI前面板
运行此VI前,先运行主机端VI和DataSocket Server。调整两个数值输入控件中的数值后,数值通过网络传输由主机端VI读取,将值设置给初值对应的局部变量,执行Runge-Kutta算法后产生新的解数据,解数据再经网络传输由客户端VI读取,产生新的误差曲线。
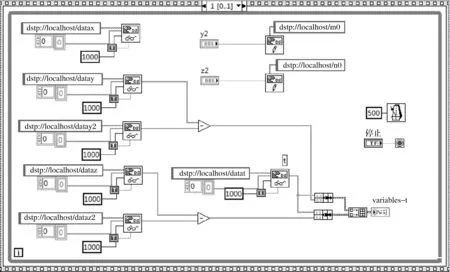
图5 客户端VI程序框图
4.3仿真结果对比
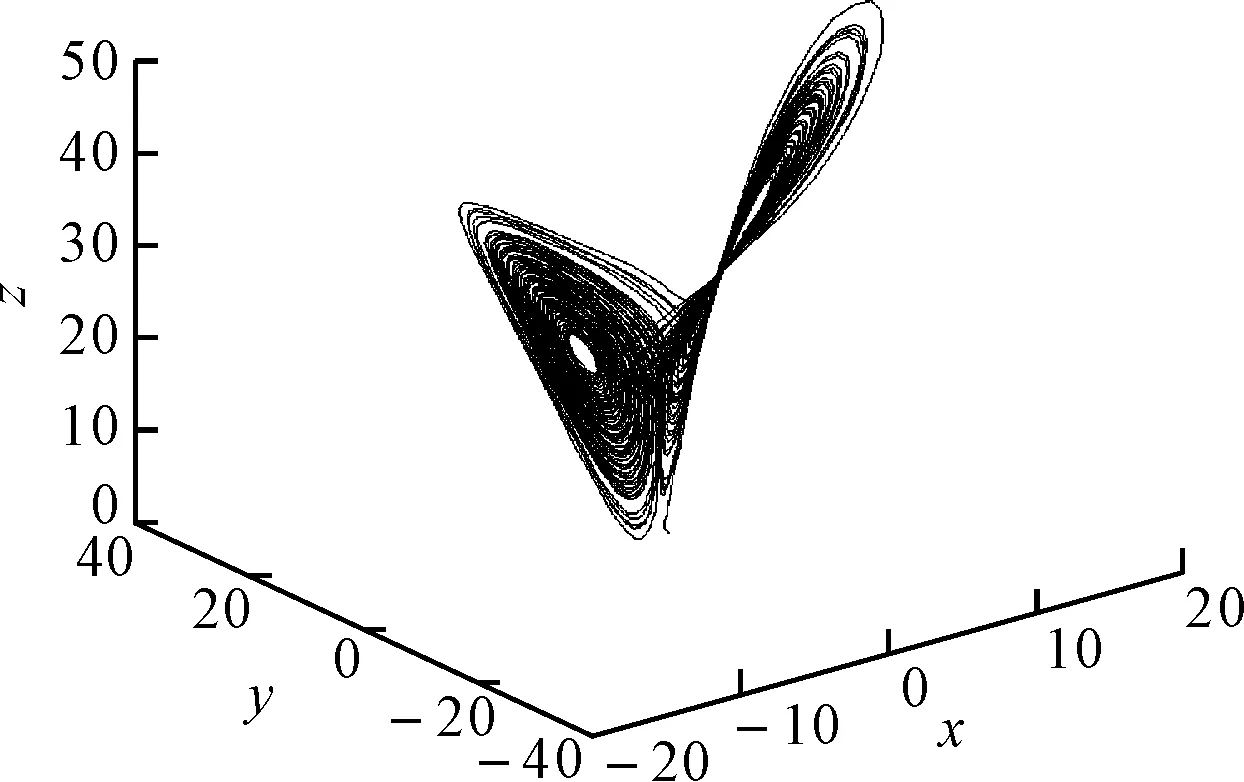
图6 Lorenz吸引子

图7 x-t波形图

图8 同步误差
为了验证仿真结果的可靠性,在Matlab中对式(4)进行仿真,参数设置与4.1节相同,仿真结果如图6~图8所示。经过对比可以发现,LabVIEW和Matlab两者的仿真结果是非常一致的,这说明LabVIEW不仅擅长于图形图像的显示,还能胜任求解微分方程一类的高级数据处理。
5 结语
本文首先研究了Lorenz系统同步原理,并在LabVIEW中实现了四阶Runge-Kutta算法仿真。针对虚拟仪器网络化趋势,比较和总结了LabVIEW中多种网络通信方式的应用场合和优缺点,最终选用基于DataSocket的网络通信方法实现主机端和客户端VI设计。VI界面友好、操作简单,通过更改相应的数值控件输入值可以方便地改变Lorenz系统的初值,从而观察不同初值时系统变量的变化,进一步掌握混沌系统同步的动力学特性;从客户端VI也可以随时通过DataSocket写入操作改变主机端VI响应子系统的初值,随后可观察相应误差信号的变化情况。经过与Matlab仿真结果的对比可以发现,LabVIEW除了优秀的图形图像处理能力外,也具备良好的信号数据处理功能,仿真结果准确、可靠。
参 考 文 献
[1] Lorenz. Deterministic Nonperiodic Flow[J]. Journal of the Atmospheric Sciences,1963,20(2):130-141.
[2] 陈仕坤,禹思敏.视频混沌加密及其FPGA实现[J].电子技术应用,2015,41(1):111-114.
CHEN Shikun, YU Simin. Video chaotic encryption and its FPGA implementation[J]. Application of Electronic Technique,2015,41(1):111-114.
[3] 邓晓衡,廖春龙,朱从旭,等.像素位置与比特双重置乱的图像混沌加密算法[J].通信学报,2014,35(3):216-223.
DENG Xiaoheng, LIAO Chunlong, ZHU Congxu, et al. Image encryption algorithms based on chaos through dual scrambling of pixel position and bit[J]. Journal on Communications,2014,35(3):216-223.
[4] 薛胜男,陈秀宏.基于混沌加密和SVD的数字图像水印算法[J].计算机工程,2012,38(19):107-110.XUE Shengnan, CHEN Xiuhong. Digital Image Watermarking Algorithm Based on Chaos Encryption and SVD[J]. Computer Engineering,2012,38(19):107-110.
[5] Matsumoto T, Chua L O, Tanaka S. Simplest chaotic nonautonomous circuit[J]. Physical Review A,1984,30(2):1155-1157.
[6] Pecora L M, Carroll T L. Driving systems with chaotic signals[J]. Phys Rev A,1991,44(4):2374-2383.
[7] Cuomo K M, Oppenheim A V, Strogatz S H. Synchronization of Lorenz-based chaotic circuits with applications to communications[J]. IEEE Transactions on Circuits and Systems Ⅱ: Analog and Digital Signal Processing,1993,40(10):626-633.
[8] 杨宏.一种基于LabVIEW的微弱信号混沌检测方法[J].西安邮电学院学报,2013,18(1):70-73.YANG Hong. A method of weak signal chaotic detection based on LabVIEW[J]. Journal of Xi’an University of Posts and Telecommunications,2013,18(1):70-73.
[9] 蔡光斌,胡昌华,蔡曦.基于虚拟检测技术的导弹武器系统维修平台研究[J].电光与控制,2007,14(2):150-153.
CAI Guangbin, HU Changhua, CAI Xi. Study on maintenance platform for missile weapon system based on virtual test technique[J]. Electronics Optics & Control,2007,14(2):150-153.
[10] 黄国兴.基于LabVIEW的网络通信方法[J].新技术新工艺,2008(10):40-42.
HUANG Guoxing. Network communication method based on LabVIEW[J]. New Technology & New Process,2008(10):40-42.
[11] 廖剑,史贤俊,张戎.在LABVIEW中实现网络通信的几种方法[J].仪器仪表学报,2008,29(8):573-576.
LIAO Jian, SHI Xianjun, ZHANG Rong. Methods of achieving network communication in LabVIEW[J]. Chinese Journal of Scientific Instrument,2008,29(8):573-576.
[12] 陈树学,刘萱.LabVIEW宝典[M].北京:电子工业出版社,2011.
CHEN Shuxue, LIU Xuan. LabVIEW bible[M]. Beijing: Publishing House of Electronics Industry,2011.
[13] 陈锡辉,张银鸿.LabVIEW 8.20程序设计从入门到精通[M].北京:清华大学出版社,2007.
CHEN Xihui, ZHANG Yinhong. LabVIEW 8.20 program designing: From novice to professional[M]. Beijing: Tsinghua University Press,2007.
收稿日期:2015年10月7日,修回日期:2015年11月22日
作者简介:谢永兴,男,博士研究生,讲师,研究方向:混沌信号处理。胡云安,男,教授,博士生导师,研究方向:模式识别与智能系统。林涛,男,硕士,副教授,研究方向:SAR成像。秦亮,男,博士,讲师,研究方向:导弹测试。
中图分类号O415.5
DOI:10.3969/j.issn.1672-9722.2016.04.044
Virtual Instrument Networking Implementation of Lorenz Chaotic Synchronizing System
XIE Yongxing1HU Yun’an1LIN Tao2QIN Liang1
(1. Department of Control Engineering, Naval Aeronautical and Astronautical University, Yantai264001)(2. Department of Scientific Research, Naval Aeronautical and Astronautical University, Yantai264001)
AbstractThe synchronization principle of Lorenz system is studied, and the forth-order Runge-Kutta algorithm is implemented in LabVIEW. After comparing several network communication methods in LabVIEW, their application sceneries, pros and cons are concluded. Both the Server VI and Client VI use DataSocket technology to achieve network communication. The interfaces are friendly and easy to operate. The results in LabVIEW are in high accordance with those in Matlab, which shows that LabVIEW is not only capable of graphical processing, but also good at advanced data processing.
Key WordsLorenz system, chaos synchronization, LabVIEW, Runge-Kutta, DataSocket network communication
