航天器光伏电池故障诊断及仿真*

李　洁　张　可

(西安工业大学电子信息工程学院　西安　710021)



航天器光伏电池故障诊断及仿真*

李洁张可

(西安工业大学电子信息工程学院西安710021)

摘要论文研究了航天器光伏电池故障诊断方法检测出故障点的问题。用小波变换方法分析光伏电池故障点；对噪声干扰情况下的故障信号进行消噪处理；结合多种小波基函数检测航天器光伏电池突变点；仿真结果表明航天器光伏电池测出的突变点就是航天器光伏电池故障点，证明了该文方法的可行性。

关键词航天器光伏电池; 小波基函数; 信号去噪; 故障诊断

Class NumberTP391

1　引言

航天器光伏电池故障诊断是指光伏电池在运行过程中，受到自然环境的影响以及自身材料老化、光伏电池不匹配等故障问题对其进行诊断，确认故障点，为后续维修工作提供便利。光伏电池的故障是无法避免的，因此对光伏电池的故障诊断就十分重要。

文献[1]在不考虑故障点的情况下，提出对光伏电池故障诊断方法可以利用卫星观察并检测光伏电池所在位置的天气情况，将卫星检测出的实际功率与模型预测进行对比，从而判断电池是否存在故障，该方法只能判断出航天器光伏电池正常与否，不能够指出发生故障的位置。文献[2]对光伏电池采用电流检测方法，设计复杂的阵列结构连接方式以实现对光伏电池故障点的定位。此方法虽然实现故障点定位，但其使用的电流传感器较多并且该阵列结构太过于复杂，在实际应用中难以实现。本文采用小波变换方法进行航天器光伏电池的故障诊断，小波变换能够克服电流检测法阵列结构复杂的缺点，应用简单无需构建阵列结构，同时具有故障点查找迅速、实用性好、成本低等优点，具备很高的研究价值。

本文在航天器光伏电池故障诊断中运用了小波变换法对航天器光伏电池电力负载信号进行检测，测出信号突变点即故障点。然后选用sure阈值模式和sym8细节系数进行小波消噪。最后，在航天器光伏电池的故障诊断实例中使用该方法进行了仿真分析，充分体现了该方法的实用性和精准性。

2　航天器光伏电池故障诊断机理

航天器光伏电池结构如图1所示。它其实是由一个大面积的P-N结，由电子(N)型半导体和空穴(P)型半导体构成。电子型半导体是硅原子与半导体杂质比如磷共同组成共价键时，施主原子的位置会有一个不能转换、固定不变的正离子。空穴型半导体是由半导体中杂质比如硼和硅原子共同组成共价键时，由于缺少一个电子故而称之为空穴。

图1　航天器光伏电池结构图

航天器光伏电池工作原理是在光伏特效应基础上的。当太阳光照在P-N结上，新的空穴-电子对形成。在内电场作用下，光生电子流向N区，光生空穴流向P区，当电路接通后就会产生电流。结合图1可以进一步得出：当能量足够大的入射光子照进P-N结过渡区时，电子被激发变成自由电子。与此同时，形成两个相反电荷的粒子。受到激发的电子在内建电场作用下，流到下方N区；由此类推，空穴在内建电场作用下，流向上方P区。因此，一个与P-N结内建电场方向相反的光生电动势和光生电场就会产生。

航天器光伏电池在太阳光照下，EVA结构会发生变化，吸收紫外线、温度、氧气能力下降。光伏电池表面透光率少，光伏电池对光能利用率降低。航天器光伏电池发生老化现象，通过故障诊断对光伏电池电力负载信号进行检测，检测电压波动幅度范围是否正常。由小波变换方法进行仿真，找寻突变点。

3　航天器光伏电池故障诊断小波变换方法

航天器光伏电池故障诊断采用小波变换方法，该方法可以确定故障点范围，为后续维修工作提供便利。故障诊断模型建立简单方便，采集光伏电池电力负载信号奇异点以及消除信号噪声都有很大的优势。为此，本文首先分析小波变换的运算机理。

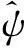
则称ψ(t)为基本小波函数或母小波函数，母小波函数还可以通过延时变换和伸缩、平移来展成一系列子小波序列:

ψa,b(t)=|a|-1/2ψ(t-b/a)

对每一个函数或者信号满足平方可积空间L2(R)这个条件，并在小波基下展开，则函数的连续小波变换(CWT)表达式为

WTf(a,b)=〈f(t),ψa,b(t)〉

小波变换对应的重构公式[5]为

对于f(t)∈L2(R)相对应的离散小波变换(DWT)方程式为

在把连续小波及连续小波变换转变成为离散小波及离散小波变换，二进制离散化后的小波和相应小波变换被称之为二进制小波或二进制小波[9]变换。

ψm,n(t)=2-m/2ψ(2-mt-nb0)

该表达式为二进小波[6]函数，其中a和b都做了二进离散。

当b0>0，ψm,n(t),m,n∈Z并不是正交的函数集，当且仅当b0=1时可得：

ψm,n(t)=2-m/2ψ(2-mt-n)

该表达式为正交函数系，也就是二进制正交小波函数系。信号函数f(t)的二进制正交小波变换的定义为

正交小波变换算法也被称为Mallat[7]算法。它是将多分辨率分析法[8]引入到小波分析中，创立了Mallat分解算法、Mallat重构算法。

由于小波基[9]与尺度函数是已知的，列出表达式：

进一步得出

也可以简化成

其中j=1,2,3,…,N。

C1=HC0,D1=GC0

C2=HC1,D2=GC1

…

Cj=HCj-1,Dj=GCj-1

(1)

式(1)就是Mallat分解算法，相对应的序列Cj,Dj为离散信号f(x)在分辨率2j下的离散逼近与离散细节。

Mallat算法的信号重构表达式如下

g0,n-2k=〈φ1,0(t),φ0,k(t)〉

g1,n-2k=〈φ1,0(t),φ0,k(t)〉

h0,n-2k=〈φ0,n(t),φ1,k(t)〉

h1,n-2k=〈φ0,n(t),φ1,k(t)〉

(2)

依据式(2)可以得出ψj,k(t)为多尺度分析的小波函数，φj,k(t)为尺度函数。

4　航天器光伏电池故障诊断实例仿真

为了验证理论分析的正确性，在Matlab软件平台对航天器光伏电池进行仿真。其系统参数设计如下：电网电压U=220V，振动幅度为100～500之间，将信号分层分解，bior3.7、db10以0.5进行依次分解。小波变换用于光伏电池传感器故障诊断[10]中进行仿真可以得到光伏电池电力负载信号波形，如图2所示，光伏电池在2200s之前时间段和3400s之后时间段趋于稳定振动幅度小，在2200s～3400s之间振动幅度大，信号不稳定产生奇异点即突变点。

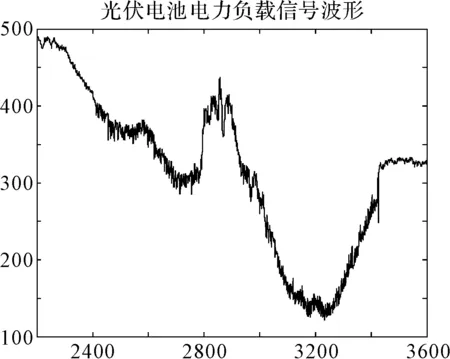
图2　光伏电池电力负载信号波形

图3　信号细节图

光伏电池电力负载信号波形如图2所示，从图可以得出当t的范围在2400～3400之间信号出现异常，这是传感器故障造成。利用bior3.7小波[11]进行3层分解，得到1～3层细节信号。时间在2400～3400之间，由于传感器故障引入了误差噪声，由图3可以看出d1高频系数重构图像要比d2、d3高频系数重构图像更加容易找到故障信号所在位置。

在光伏电池正常运作时，其正常输出点的采样信号为蠕变信号。一旦系统发生故障时，输出信号会出现突变信号。主要表现在幅度和频率的突变，从正常到出现故障的一系列采样序列分析可得。

图4　光伏电池小波分解层次图

采用小波分析法来分析检测信号的突变点。从图4中可得光伏电池小波分解的层系数，当t=500时，系统工作出现了异常情况；在t=1000时，系统又恢复了正常。

在测量信号中总是会受到噪声干扰，则需要考虑降低噪声对系统的干扰。引入小波消噪法。一般来说，利用小波分析的消噪方法分为三个步骤如下：

1) 对噪声信号进行正交小波变换计算，确定一个合适小波分解层次和小波基函数。对信号进行N层小波分解，获得相应的小波分解系数。该系数包括高频系数以及低频系数。

2) 高频系数的阈值量化：选择一个阈值量化准则，对每一层小波系数进行阈值量化处理。

3) 小波重构：经阈值处理后的小波系数获得恢复后的原始信号估计值，依据小波分解第N层的低频系数和处理后的第1层到第N层的高频系数，进行尺度信号的小波重构。

对光伏电池进行小波消噪处理如图5、6所示。

由图5中可以看出利用sym8和db10进行降噪[12]后基本恢复到原始信号，消噪效果显著。但与此同时，从图中可以看到采用阈值消噪后信号特征值比较少，以至于很难非常准确地将原始信号反应出来。从图6和图7可以得到db10对信号的5层分解以及从第5层到第1层的低、高频系数重构图。

图5　原始信号、叠加随机噪声、db10和sym8默认阈值降噪后信号图形

图6　db10对信号进5层分解

图7　分解的第5层到第1层的低频、高频系数重构图

从图6和图7中可以看出，db10对信号进行5层分解，然后对第5层到第1层的高频系数和低频系数进行重构。图中细节信号是由白噪声[13]分解得出的，所需的正弦信号是可以由图6中的近似信号a5得出，因此获得的信号就是原始信号波形，这样就把隐藏在噪声中的有效信号分离出来。

Matlab软件[14]中自带noissin信号函数以及初始信号，对光伏电池进行小波去噪仿真。在noissin信号函数上叠加一个随机噪声信号得到e,本文采用db10小波和sym8小波对随机噪声信号e进行5层分解，选用minimaxi阈值模式和db10作为细节系数和选择sure阈值模式和sym8作为细节系数进行对比。噪声去除后，对初始信号进行分析，将噪声信号和原始信号分离出来。

5　结语

结合小波变换信号奇异点检测方法，对航天器光伏电池故障点进行检测，并通过实例验证了该方法可行性。通过理论分析，选用db10和bior3.7作为小波基函数，对航天器光伏电池电力负载信号进行故障点定位，用sym8小波对航天器光伏电池电力负载信号进行消噪处理。仿真结果表明，航天器光伏电池在三种小波基函数下可以快速准确地定位故障点。仿真验证了该方法的有效性和可行性。在今后的研究中，此方法具有长远意义。

参 考 文 献

[1] 程泽，李兵峰，刘力，等.一种新型结构的光伏阵列故障检测方法[J].电子测量与仪器学报，2010,24(2):31-136.

CHENG Ze, LI Bingfeng, LIU Li, et al. A novel structure of PV array fault detection method for[J]. Electronic Measurement and Instrumentation,2010,24(2):31-136.

[2] 陈中华，赵敏荣.硅太阳能电池数学模型的简化[J].计算机仿真，2006,23(6):239-243.

CHEN Zhonghua, ZHAO Minrong. Mathematical model of silicon solar cell simplified[J]. Computer Simulation,2006,23(6):239-243.

[3] Vetterli M, et al. Wavelet and filter banks: Theory and design[J]. IEEE. SP,1992,40(9):14-38.

[4] 冉启文，谭立英.小波分析与分数傅里叶变换及应用[M].北京：国防工业出版社，2002:12-30.

RAN Qiwen, TAN Liying. Wavelet analysis and fractional Fourier transform and application[M]. Beijing: National Defense Industry Press,2002:12-30.

[5] 程正兴.小波分析算法与应用[M].西安：西安交通大学出版社，1998:40-50.

CHENG Zhengxing. Wavelet analysis algorithm and application[M]. Xi’an: Xi’an JiaoTong University press,1998:40-50.

[6] Resenikoff H L. Wavelets and Adaptive Signal Processing[J]. SPIE. Adaptive Processing,1991,1565:370-382.

[7] Mallat S. Multifrequency channel decomposition of images and wavelet models[J]. IEEE ASSP,1989,37:2091-2110.

[8] Young R K. Wavelet Theory and Its Application[J]. Boston Kluwei Academic Publisher,1993:12-20.

[9] Kadambe S, et al. Application of the wavelet transform for pitch detection of speech signals[J]. IEEE IT,1992,38(2):917-924.

[10] 石启星，田金文，柳健.小波变换及其在信号处理中的应用.遥测遥控[J].1996,17(3):56.

SHI Qixing, TIAN Jinwen, LIU Jian. Wavelet transform and its application in signal processing. Remote control[J]. 1996,17(3):56.

[11] 周小勇，叶银忠.小波分析技术在故障诊断中的应用[J].上海海运学院学报,2001:9-12.

ZHOU Xiaoyong, YE Yinzhong. Application of wavelet analysis in fault diagnosis[J]. Journal of Shanghai Maritime University,2001,9-12.

[12] 董小刚，秦喜文.信号消噪的小波处理方法及其应用[J].吉林师范大学学报(自然科学版),2003,5(2):14-60.

DONG Xiaogang, QIN Xiwen. Wavelet processing method for signal de-noising and its application[J]. Journal of Jilin Normal University(Natural Science Edition),2003,5(2):14-60.

[13] 刘鲭洁，陈桂明，刘晓方,等.FFT和小波变换信号降噪中的应用[J].数据采集与处理，2009,24(10):58-60.

LIU Qingjie, CHEN Guiming, LIU Xiaofang, et al. Application of.FFT and wavelet transform signal denoising in[J]. Data Acquisition and Processing,2009,24(10):58-60.

[14] 胡昌华，李国华,等.基于MATLAB的系统分析与设计，小波分析[M].西安：西安电子科技大学出版社，2004:35-40.

HU Changhua, LI Guohua et al. Analysis and design of system based on wavelet analysis MATLAB[M]. Xi’an: Xi’an Electronic and Science University press,2004:35-40.

收稿日期:2015年10月8日,修回日期:2015年11月28日

基金项目:陕西省国际科技合作重点项目(编号：2015KW-024)资助。

作者简介:李洁，女，硕士研究生，研究方向：故障诊断、随机控制、最优控制、自适应控制等。张可，男，硕士研究生，研究方向：故障诊断。

中图分类号TP391

DOI:10.3969/j.issn.1672-9722.2016.04.038

Fault Diagnosis and Simulation of Photovoltaic Battery for Spacecraft

LI JieZHANG Ke

(School of Electronic and Information Engineering, Xi’an Technology University, Xi’an710021)

AbstractThe spacecraft fault diagnosis method of photovoltaic cells is studied to detect the fault point. Wavelet transform method is used to analyze photovoltaic battery point of failure. The noise conditions for fault signal are denoised. Many kinds of wavelet basis function test spacecraft photovoltaic cell mutation point are combined. The simulation results show that the spacecraft is the abrupt change point of the pv cells detect spacecraft photovoltaic battery failure point, proves the feasibility of this method.

Key Wordsspacecraft photovoltaic cell, wavelet base function, signal denoising, fault diagnosis