基于多源测量与属性混合信息的分类识别方法*

关　欣　常　进　王　虹　衣　晓

(海军航空工程学院电子信息工程系　烟台　264001)



基于多源测量与属性混合信息的分类识别方法*

关欣常进王虹衣晓

(海军航空工程学院电子信息工程系烟台264001)

摘要充分利用多传感器系统提供的多源异类信息,将观测数据处于数据级的属性和处于特征级的属性混合作为描述目标的特征矢量;对特征矢量进行了主成分分析,在此基础上转换至三维直角坐标系寻找最优分类平面进行分类识别;采用“一对一”策略解决多类分类问题;通过仿真实验验证了该方法在加入不同百分比高斯白噪声环境下的有效性,并与BP神经网络识别方法在同等条件下作了对比实验,突出了论文所提方法正确识别率高、识别速度快和稳定性高的优越性。

关键词主成分分析; 最近顶点规则; 最优分类平面; BP神经网络

Class NumberTP391

1　引言

多传感器提供的观测数据在属性上可以是同类的也可以是异类的;在粒度级别上可以是稀疏的,也可以是稠密的,也可能分别处于数据级、特征级或是符号级各种不同的抽象级别上。因此异类多传感器与同类传感器相比,其提供的信息具有更强的多样性和互补性[1～2]。在进行目标识别[3]时可充分利用多传感器提供的多源异类信息,仅仅采用常规的属性特征参数进行分类识别已经突显单一,并且模式匹配法、k-近邻分类法等传统识别方法不但计算量大,识别准确率低,而且还需进行专家校验[4]。因此,除了利用常规的观测数据处于数据级的属性,还可以充分挖掘特征级的属性,将二者混合作为描述目标的特征矢量。

本文首先利用多源异类信息构造描述目标的特征矢量,即为目标的模式。然后在对数据样本特征矢量进行主成分分析(Principal Component Analysis,PCA)的基础上,合理地变换至三维直角坐标系通过空间几何分析(Space Geometrical Analysis,SGA)进行分类识别。最后通过仿真实例和对比实验,验证了基于多源测量与属性混合信息的分类识别方法的有效性和优越性。

2　特征矢量的构建

特征提取或特征矢量的构建是进行模式识别的关键问题之一。特征矢量选取的好坏直接影响着分类器的分类识别结果[5]。选取由j个属性的观测数据构成的数据样本特征矢量x对目标进行数学抽象描述,并记为:

x=(x1,x2,…,xj1,xj1+1,xj1+2,…,xj)T

(1)

其中,属性1,2,…,j1的观测数据x1,x2,…,xj1处于数据级;而属性j1+1,j1+2,…,j的观测数据xj1+1,xj1+2,…,xj处于特征级,表示具有或不具有某种性质特征。为了使后续设计的分类器具有识别能力,必须要把xj1+1,xj1+2,…,xj转换成数值型参数。因此可以利用二值函数来表示,即用“1”表示具有某种性质特征、“0”表示不具有该性质特征。而后续分类器设计中需要求协方差矩阵,这里进一步把“1”和“0”的二值性用区间长度为1且不同区间内的服从均匀分布的随机数来代替。这里区间的选取应视数据x1,x2,…,xj1具体的数量级而定,只要数量级处于这些数据数量级之间即可,不至于因过小而被削弱其作用或过大而被过分利用。

3　基于多源测量与属性混合信息的分类识别方法原理及步骤

该方法首先根据上述特征矢量构建方法得到两类样本,其次求取两类样本的整体协方差矩阵,并依据主成分分析方法得出各个样本由第一、第二、第三主成分构成的三维主成分向量,再次将所有主成分向量对应至三维直角坐标系中的点,然后通过空间几何方法找到一个最优分类平面将两类点分开,根据样本坐标点与最优分类平面的位置关系,对样本完成分类识别,最后采用“一对一”策略解决多类分类问题。我们将这个处理过程简记为PCA-SGA,该方法流程图如图1所示。

按照图1,本方法的详细步骤如下:

Step1:根据PCA求各样本的主成分向量

根据式(1),把第i个样本进一步记为

(i=1,2,…,N1,N1+1,…,N)

(2)

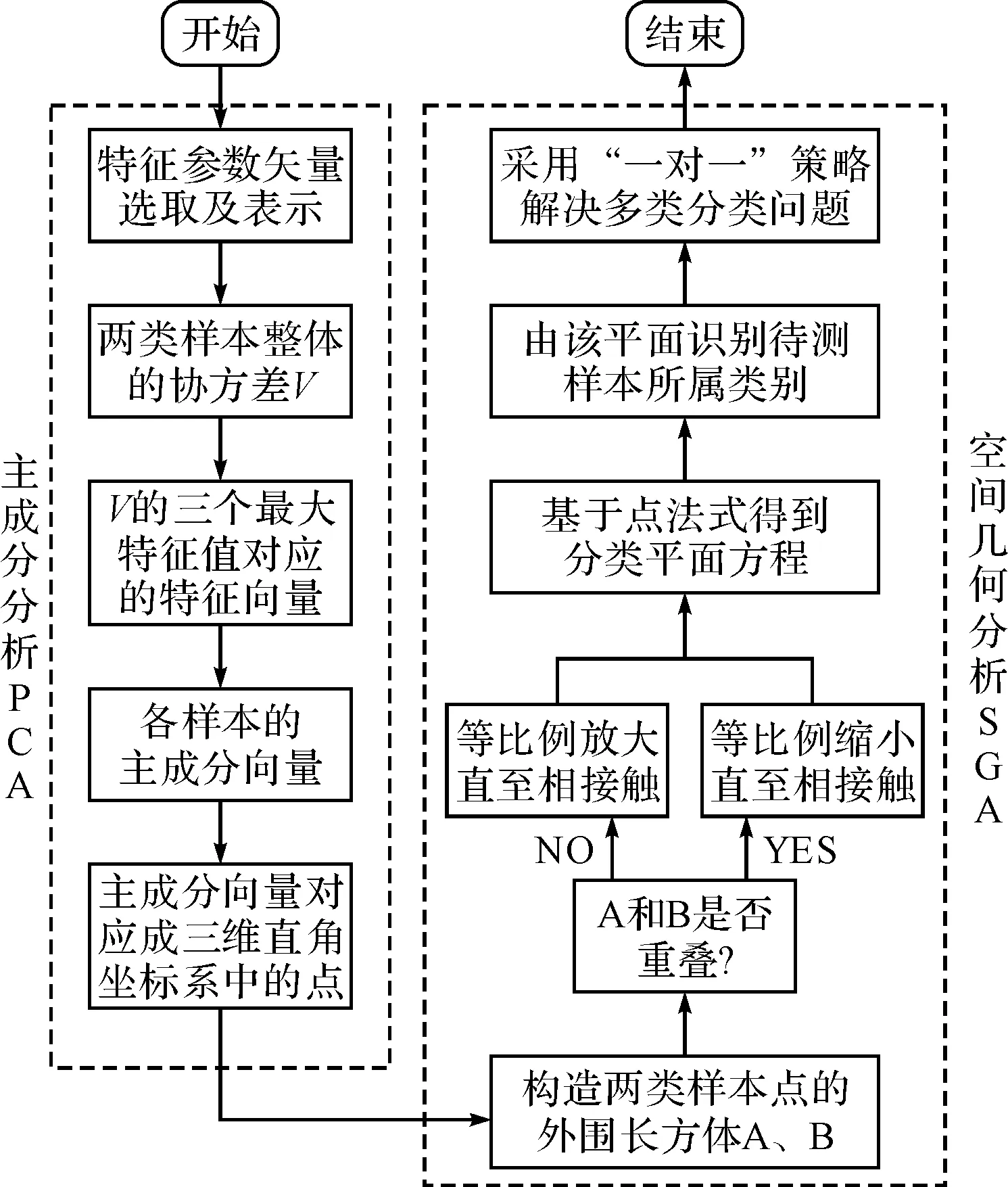
图1　基于多源测量与属性混合信息的分类识别方法流程图

记第1类样本和第2类样本的整体协方差矩阵为V:

(3)

记V的特征值为λ1≥λ2≥…≥λj,且前三个最大特征值即λ1,λ2,λ3对应的特征向量分别为p1,p2,p3。则由x(i)(i=1,2,…,N)的第一、第二、第三主成分构成的主成分向量为

(i=1,2,…,N)

(4)

Step2:将主成分向量对应至坐标系点,并构造最小的轴向长方体A和B分别把两类坐标点包围起来

建立一个以前三个主成分y1,y2,y3分别为横轴、纵轴、竖轴的三维直角坐标系,将N个样本的主成分向量对应成坐标系中的N个点,在坐标系中可以直观地反映出第1类样本和第2类样本的分布情况。

以第1类样本为例,将y(1),y(2),…,y(N1)对应至坐标系中的N1个点后,构造一个最小的长方体A将这N1个点包围起来,并且使A各棱线均平行或垂直于每条坐标轴,即经平移后可使共某个顶点的三条棱线与三条坐标轴对应重合。这样既方便快速得到A又可以覆盖y各分量在范围内的所有组合。将这样的长方体定义为轴向长方体,记A的长宽高分别为L1、W1、H1,则有:

(5)

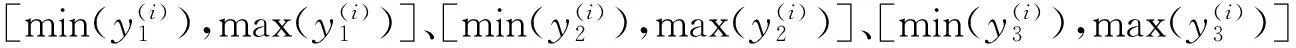
(6)

Step3:根据最近顶点规则放大或缩小A和B至恰好相接触

如果两类样本属性很接近乃至出现混叠时,A和B很有可能出现重叠现象。因此,具体步骤要分A和B是否有重叠两种情况。

1) 若两长方体没有重叠即A∩B=∅

记A的8个顶点为Ai(i=1,2,…,8),B的8个顶点为Bj(j=1,2,…,8),则A和B最接近的两个顶点可由式(7)获得:

(7)

则Ai0和Bj0即为所求。

保持A和B几何中心不变,按下述方法放大A、B至恰好相接触:记(Δy11,Δy12,Δy13)=Ai0-M,(Δy21,Δy22,Δy23)=Bj0-M,显然有|Δ11|=|Δ21|,|Δ12|=|Δ22|,|Δ13|=|Δ23|。则A和B的长宽高各自的放大比例为

(8)

(9)

记放大后的A、B分别为A′、B′,此时A′和B′恰好相接触,称这种方法为最近顶点规则。

2) 若两长方体存在重叠即A∩B≠∅

此种情况下同样可以按最近顶点规则将A和B缩小至恰好相接触。缩小的方法和1)中放大的方法相似,首先根据式(7)得到最近两顶点,从而找到其中点,然后由式(8)得到A和B的长宽高各自的缩小比例,最后A和B的长宽高分别缩小至L″1、W″1、H″1和L″2、W″2、H″2:

(10)

但需要强调的是这只适用于重叠部分长方体的长宽高均小于A和B的长宽高的一半,更严重的重叠情况这里暂且不作讨论。

Step4:根据点法式方程寻找最优分类平面分离A和B

(11)

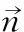
表1　法向量的取值情况

Step5:根据最优分类平面判别样本所属类别

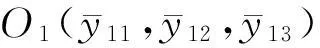
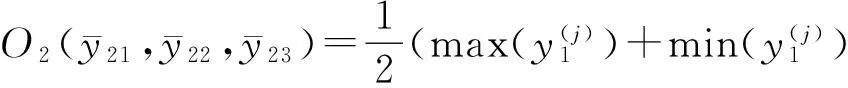
(i=1,2,…,N1,j=N1+1,N1+2,…,N)

(12)

将O1和O2坐标分别代入由式(11)所得的平面方程,取其数值符号记为sign1、sign2:

sign1=sign(F(O1))

sign2=sign(F(O2))

(13)

平面两侧的点代入平面方程后的数值符号是相反的,则sign1和sign2为一正一负。所以可以通过样本的主成分向量对应坐标点代入平面方程后的数值符号来判定该样本所属类别。

假设待分类样本为x,其分类识别方法如下:

1) 把x代入式(4)得到主成分向量yx=(yx1yx2yx3);

2) 将上述主成分向量yx对应到三维直角坐标系中的点Q(yx1,yx2,yx3),并把Q代入式(11)平面P方程,则x的分类识别依据为:

若F(yx1,yx2,yx3)=sign1,则将x分类识别为第1类;若F(yx1,yx2,yx3)=sign2,则将x分类识别为第2类。

Step6:根据“一对一”策略解决多类分类问题

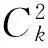
至此,一种基于多源测量与属性混合信息的分类识别方法的整个过程结束。

4　仿真实验

从相关数据库中选取四种典型的且属性参数较为接近的目标进行仿真实验,属性参数取值范围如表2所示。其中,属性1、2、3的观测数据处于数据级,而属性4、5的观测数据处于特征级;目标1和2同时具有某两种性质特征,而目标3和4均不具有这两种性质特征;目标4属性2的参数值为序列长度为18的序列类型:[1080,1080+Δd,1080+2Δd,…,1420,1420-Δd,1420-2Δd,…,1080+Δd](Δd=(1420-1080)/9)。根据前3个属性观测数据的数量级,则目标在属性4和5上同时具有某两种性质特征和不具有这两种性质特征时的观测数据x4和x5可按式(14)数值化描述(取其他相当的区间得到的分类识别结果与本文相差很微小),其中unifrnd(a,b)(其中a≤b)表示在[a,b]上服从均匀分布的随机数。

(14)

在Matlab仿真环境下,各类随机产生1000个样本,其中600个样本作为训练样本,400个样本作为测试样本。单个样本各属性均为实数型数据,足够多的训练样本可以更好地表征数据库目标各属性可能的实数型、区间型和序列类型的混合型数据[12]。单次量测值(即一个测试样本)加入训练好的分类器中进行分类识别则转化为简单的实数-实数同类数据的识别,无需进行异类数据的同型转化[13]。

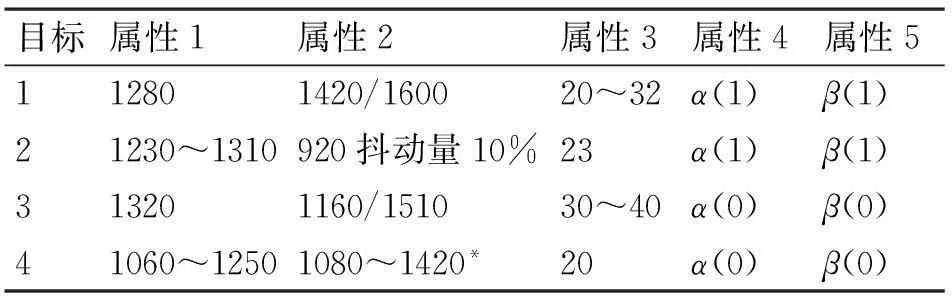
表2　各目标属性特征参数表

基于“一对一”策略,四类训练样本可分解成六个简单的两类分类问题。按照PCA-SGA步骤可得到六个不同的最优分类平面P,且前三个主成分的累计贡献率均超过85%。两类分类问题得到的A′和B′如图2所示。

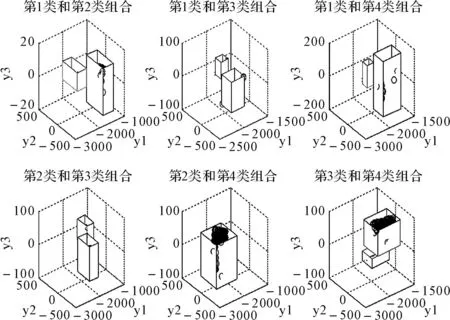
图2　两两组合构成的A′和B′

由于传感器工作环境的不确定性因素,导致观测数据一般包含有噪声成分。为更符合观测数据的实际情况,将测试样本属性1、2、3的观测数据加上高斯白噪声。然后把每一个测试样本依次加入到六个两类分类模型中进行分类识别,根据次数最高确定各个测试样本最终属于的类别。在2%、5%、10%三种不同的高斯白噪声环境下均进行100次蒙特卡洛仿真,将正确识别出的测试样本个数与测试样本总个数的比值作为正确识别率,则不同噪声环境下各目标正确识别率、平均正确识别率及识别时间结果如表3所示。

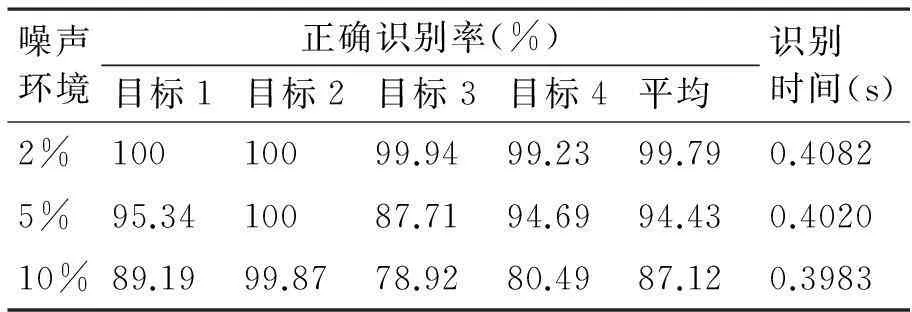
表3　本文方法识别结果

为了验证该方法的优越性,将其与BP神经网络识别方法在同等条件下进行对比实验。训练样本和测试样本的选取同上。神经网络参数及训练参数设置如下:输入数据为5维数据,隐含层节点数为11,输出层节点数为4,隐含层节点转移函数为正切S型传递函数,输出层节点转移函数为线性传递函数,最小均方误差为10-8,最小梯度为10-20,训练次数选为20次[4,14]。同样在2%、5%、10%三种高斯白噪声环境下均进行100次蒙特卡洛仿真,最终实验结果如表4所示。

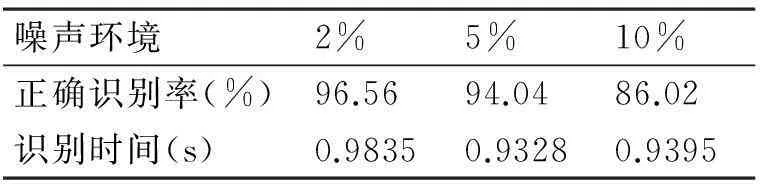
表4　BP神经网络识别结果

对比表3和表4可知,本文方法在三种噪声环境下的识别率均要高于BP神经网络模式识别方法,且识别时间少于一半,识别速度明显更快。另外,图3给出了在三种噪声环境下,本文方法和BP神经网络进行100次蒙特卡洛仿真的识别率稳定性对比。由图3对比发现,本文方法100次蒙特卡洛仿真的运行结果波动范围很小,基本趋于稳定,而BP神经网络模式识别方法的运行结果波动范围较大,甚至出现个别识别率严重低于平均值的现象,稳定性较差。

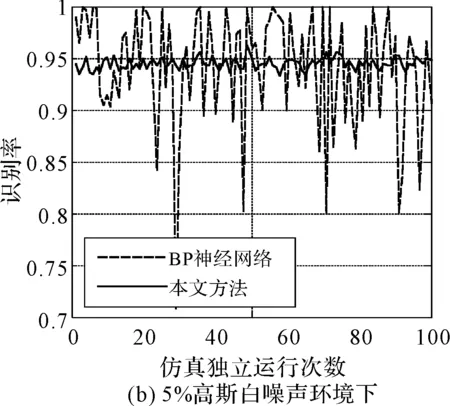
图3　三种高斯白噪声环境下的识别率稳定性对比

5　结语

本文将具有不同类型观测数据的属性混合作为特征矢量,通过主成分分析用三维的主成分向量表示高维数据样本特征矢量的变化特性,并未将特征参数样本矢量通过一个非线性映射变换到一个更高维的特征空间,整个过程也未涉及复杂的数学算法和函数,所以计算相对简单快捷,可以实现快速分类识别。另外,通过一个空间平面来隔开两类样本的主成分向量坐标点,这种几何结构关系较为稳固,进行多次独立重复试验的结果相差甚小,总体趋于平缓稳定。

参 考 文 献

[1] 韩崇昭,朱洪艳,段战胜.多源信息融合[M].第二版.北京:清华大学出版社,2010:11-12,479.HAN Chongzhao, ZHU Hongyan, DUAN Zhansheng, et al. Multi-sensor Information Fusion[M]. Second Edition. Beijing: Tsing University Press,2010:11-12,479.

[2] 于昕,韩崇昭,潘泉,等.一种基于D-S推理的异源信息目标识别方法[J].系统工程与电子技术,2007,29(5):788-790.

YU Xin, HAN Chongzhao, PAN Quan, et al. Method Based on Evidenve Theory for Multi-source Target Recognition[J]. Systems Engineering and Electronics,2007,29(5):788-790.

[3] 何友,王国宏,陆大紟,等.多传感器信息融合及应用[M].第二版.北京:电子工业出版社,2007:4-5.

HE You, WANG Gonghong, LU Dajin, et al. Multisensor Information Fusion With Application[J]. Second Edition. Beijing: Publish House of Electronics Industry,2007:4-5.

[4] 樊亚春,王岩,才迎光,等.基于支持向量机的相控阵雷达信号识别方法[J].电子信息对抗技术,2014,29(5):44-48.

FAN Yachun, WANG Yan, CAI Yingguang, et al. The Recognition Method of Phased-Array Radar Signal Based on Support Vector Machine[J]. Electronic Information Warfare Technology,2014,29(5):44-48.

[5] 姚旭,王晓丹,张玉玺,等.特征选择方法综述[J].控制与决策,2012,27(2):161-166,192.

YAO Xu, WANG Xiaodan, ZHANG Yuxi, et al. Summary of Feature Selection Algorithms[J]. Control and Decision,2012,27(2):161-166,192.

[6] Jollife I. Principal Component Analysis[M]. New York: Springer-Verlag,1986:10-28.

[7] 吴翊,李永乐,胡庆军.应用数理统计[M].长沙:国防科技大学出版社,2008:285-298.WU Yi, LI Yongle, HU Qingjun. Applied Mathematical Statistics[M]. Changsha: NUDT Press,2008:285-298.

[8] K.-T. Kim, I.-S. Choi, H.-T. Kim. Efficient Radar Target Classification Using Adaptive Joint Time-frequency Processing[J]. IEEE Trans Antennas Propagat,2000,48(12):1789-1801.

[9] 范雪莉,冯海泓,原猛.基于互信息的主成分分析特征选择算法[J].控制与决策,2013,28(6):915-919.

FAN Xueli, FENG Haihong, YUAN Meng. PCA Based on Mutual Information for Feature Selection[J]. Control and Decision,2013,28(6):915-919.

[10] Yong Xu, David Zhang, Zhong Jin, et al. A Fast Kernel-based Nonlinear Discriminant Analysis for Multi-class Problems[J]. Pattern Recognition,2006,39:1026-1033.

[11] 徐勇,杨强,杨静宇.基于核的快速特征抽取及识别方法[J].解放军理工大学学报:自然科学版,2005,6(2):128-131.

XU Yong, YANG Qiang, YANG Jingyu. Fast Kernel-based Feature Extraction and Recognition[J]. Journal PLA University of Science and Technology: Natural Science,2005,6(2):128-131.

[12] 刘海军,李悦,柳征,等.基于随机文法的多功能雷达识别方法[J].航空学报,2010,31(9):1809-1817.

LIU Haijun, LI Yue, LIU Zheng, et al. Approach to Multi-function Radar Indentification Based on Stochastic Grammars[J]. Acta Aeronautica Astronautica Sinica,2010,31(9):1809-1817.

[13] 关欣,孙贵东,衣晓,等.累积量测序列的区间云变换及识别[J].控制与决策,2015,30(8):1345-1355.

GUAN Xin, SUN Guidong, YI Xiao, et al. Interval Cloud Transform and Recognition Research of Accumulative Measurement Sequence Data[J]. Control and Decision,2015,30(8):1345-1355.

[14] 孙即祥.现代模式识别[M].长沙:国防科技大学出版社,2010:285-288.

SUN Jixiang. Modern Pattern Recognition[M]. Changsha: NUDT Press,2010:285-288.

收稿日期:2015年10月7日,修回日期:2015年11月25日

基金项目:国家自然科学基金重点项目(编号:61032001);教育部新世纪优秀人才支持计划项目(编号:NCET-11-0872)资助。

作者简介:关欣,女,博士,教授,研究方向:智能信息处理、多源信息融合。常进,男,硕士,研究方向:相控阵雷达辐射源识别。王虹,女,硕士,研究方向:雷达辐射源识别。衣晓,男,博士,教授,研究方向:多传感器信息融合、多目标跟踪、组合导航。

中图分类号TP391

DOI:10.3969/j.issn.1672-9722.2016.04.012

Classification and Recognition Method of Information Based on Multi-source Measuring and Attributes Mixing

GUAN XinCHANG JinWANG HongYI Xiao

(Department of Electronics and Information Engineering, Naval Aeronautical and Astronautical University, Yantai264001)

AbstractMulti-source and heterogeneous information provided by multisensor system is being utilized fully. The paper merges attributes whose observation data is at data level and somes at feature level into a feature vector that describes target. On the basis of principal component analysis of feature vector, it is transformed to triangular rectangular-coordinates system to find a optimal separating plane for classification and recognition. “One-Against-One” strategy is used to deal with the multi-class problems. The validity of the method is validated by simulation experiments in the environment of different percentages of gaussian white noise, then this paper carrys on comparison experiment with BP neural network recognition method in same condition. It shows the superiority of higher recognition rate, faster recognition speed and higher stability of the proposed method.

Key Wordsprincipal component analysis, nearest peak regulation, optimal separating plane, BP neural network