中国地面气温统计降尺度预报方法研究

陈国华,郭品文

南京信息工程大学 气象灾害教育部重点实验室,江苏 南京 210044



中国地面气温统计降尺度预报方法研究

陈国华*,郭品文

南京信息工程大学 气象灾害教育部重点实验室,江苏 南京 210044

2013-02-06收稿，2013-05-16接受

公益性行业(气象)科研专项(GYHY201006017)

摘要利用中国752个基本、基准地面气象观测站2000—2010年地面温度日值数据,采用具有自适应特征的Kalman滤波类型的递减平均统计降尺度技术,对中国地面温度进行精细化预报研究。分析该方案的降尺度效果,并与常用插值降尺度方法进行比较。结果表明:1)递减平均统计降尺度技术相比插值方法有较大的提高,显著减小东西部预报效果差异,1～3 d预报的均方根误差减小了1.4 ℃;2)该方案1～3 d预报的均方根误差为1.5 ℃,预报误差从东南地区(均方根误差为1.4 ℃)向西北地区(均方根误差为1.8 ℃)逐渐增大,并且预报效果夏季优于冬季。因此,递减平均统计降尺度技术对中国地面温度进行精细化预报是可行的。

关键词

精细化预报

统计降尺度

插值

递减平均法

实现精细化天气预报最关键和有效的技术手段就是降尺度技术,主要有嵌套高分辨率数值模式的动力降尺度技术和基于现有大尺度数值产品的统计降尺度技术(刘永和等,2011)。动力降尺度的物理意义明确,是长期发展的根本方向,但它的缺点是消耗的计算量大,模式的性能受所提供的边界条件的影响很大,并且预报效果还达不到精细化预报和服务的需求(陈豫英等,2005)。就上述缺陷,目前各国学者主要使用统计降尺度方法解决。统计降尺度通过建立不同尺度间的关系来实现尺度间的转换,其优点在于它可以和现有数值模式产品相配合,能较好地解决现有动力降尺度法的不足,计算量小、容易实现,是提高气象要素精细化预报水平更为直接有效的手段。Kidson and Thompson(1998)和Mearns et al.(1999)均用统计降尺度和动力降尺度两种方法进行气候预测,认为动力降尺度虽有更好的物理基础作为支撑,但统计降尺度消耗的计算量小,很多方面更为可取。

常用的统计降尺度方法主要概括转换函数法、环流分型技术和天气发生器(李江萍和王式功,2008)。应用最多是转换函数法,它包括了多元线性回归、SVD等线性转换函数法(Oshima et al.,2002;范丽军等,2007)和人工神经网络、支持向量机等非线性转换函数法(Mpelasoka et al.,2001;Anandhi et al.,2009)。Huth et al.(2008)通过对比线性回归与神经网络两种方法进行温度降尺度,证明了线性方法也可以取得较好的降尺度效果。Lian et al.(2010)运用PCA、CCA等统计降尺度方法,利用1960—1990年的月平均海平面气压和温度值成功预测中国沿海地区气温。贾小龙等(2010)使用变形的典型相关分析方法对中国冬季温度进行了可预报性研究,很好地揭示了大气环流和温度的内在联系,并且预测效果明显高于模式输出结果。但目前而言,上述研究方法主要运用于气候预测方面(陈威霖等,2012)。

对于短期天气预报的统计降尺度研究,目前依然比较匮乏。国内主要采用双线性插值、Kriging插值、反距离权重插值等空间内插方法(李新等,2000;钞振华,2011;彭彬等,2011;徐振亚等,2012)和滑动训练法等(智协飞等,2013)进行统计降尺度研究,此外还有学者使用一些简单的转换函数(郭虎等,2008),但均有一定局限性。近年来国外主要采用Kalman滤波、滑动窗等偏差估计方法(Engel and Ebert,2011;Monache et al.,2011)对气象要素进行统计降尺度研究。Cui et al.(2011)等提出了一种具有自适应特征的Kalman滤波类型的递减平均统计降尺度技术,对北美集合预报系统的输出值做统计后处理,获得精细化预报产品,取得明显效果。

本文将上述递减平均统计降尺度技术运用于中国进行地面气温的精细化预报试验,探索该方案在中国的可用性,以及研究其与插值降尺度方法预报能力的差异。

1　资料和方法

1.1资料

本文所用资料为中国752个基本、基准地面气象观测站的地面日平均温度数据,资料时段为2000—2010年,选取其中缺测较少的600站进行预报试验。

1.2降尺度方案设计

1.2.1预报场和分析场的建立

数值预报产品自身带有系统性偏差和随机误差,使得基于数值产品的精细化预报的误差不仅源于降尺度过程,也来源于数值产品本身,最终导致难以评价该降尺度方案的优劣以及效果的好坏。出于上述考虑,本文将使用地面气象观测站的站点观测数据构建“预报场”和“分析场”,以去除数值预报产品带来的误差。首先,在上述所选的600站中较均匀地随机挑选100站作为低分辨率“预报场(F100)”,代替业务中所使用的低分辨率的大尺度模式产品,剩余的500个观测站作为高分辨率的“精细化分析场(A500)”。然后,将低分辨率“预报场”的日平均温度使用空间内插的方法插值到“精细化分析场”的站点上,作为精细化初估场(F500)。具体台站分布见图1,“·”表示低分辨率“预报场(F100)”,“+”表示高分辨率的“精细化分析场(A500)”。

图1　预报试验所选的600个站点分布Fig.1　Distribution of the selected weather stations for the forecasting test

大多数研究认为,数据密度、数据分布和空间异质性是影响插值精度的主要因素,插值方法的选择不是绝对的、唯一的(Lam,1983)。考虑到是在不规则的站点间进行插值计算,双线性插值和样条插值等空间内插方法不适用,本文选用反距离插值(文中以IDW表示,下同)、距离平方反比权重插值(IDS)、Cressman客观分析(Cressman)和Kriging插值(Kriging)4种方法(林忠辉等,2002)对低分辨率“预报场(F100)”进行空间内插,获取精细化初估场(F500)。

将4种插值结果与“精细化分析场(A500)”进行比较分析可以发现(图2),整体而言不同插值方法的效果随时间的变化基本一致,春、冬季误差较大,秋季最小。Kriging插值和IDS插值的准确度明显优于IDW插值和Cressman插值,前两种插值的均方根误差的年平均值接近3.0 ℃,较后两者减小了0.1 ℃左右;相比之下,Kriging插值效果略优于IDS插值,但两者十分接近。考虑到IDS插值比Kriging插值更为实用和简洁,且效果相差无几,故本文选择距离平方反比权重插值(IDS)进行空间内插,获取精细化预报的初估场(F500)。

图2　不同插值方法的均方根误差Fig.2　RMSE of different interpolation methods

1.2.2降尺度矢量(DV)的构建

降尺度矢量DV体现了精细化初估场(F500)与精细化分析场(A500)之间的统计关系,定义为同一时刻F500与A500间的差值场,即DV(t)=F500(t)-A500(t),t为某一时刻。

DV(t0)=(1-w)×DV(t-1)+w×(F500(t0)-A500(t0))。

(1)

如公式(1),DV通过递减平均法进行更新,t0表示起报时刻;t-1表示前一个起报时刻;w为自适应系数,在0～1之间,反映不同时刻的DV对于t0时刻的贡献大小,即过去多长时间的信息将对预报当天的订正有影响。

前人的研究成果(王辉赞等,2006)表明,Kalman滤波方法对于连续性变量较其他统计预报方法的自适应能力更强,能够更好地跟踪预报对象。本文所使用的递减平均统计降尺度技术即为Kalman滤波类型的方法,通过提取历史预报和实况之间的误差信息,估算系统偏差,使得预报更为接近观测值。递减平均法初始化偏差的方法分为偏差“热启动”和偏差“冷启动”两种。所谓偏差“热启动”,就是利用过去一定天数的F500(t)与A500(t)差值的时间平均值作为偏差的初始值;出于计算方便或者资料不足等原因,将偏差的初始值直接设为0,即为偏差“冷启动”。本文将使用后者进行偏差初始化(李莉等,2011)。

1.2.3降尺度预报值DF

DF(t)=F500(t)-DV(t0)。

(2)

公式(2)中,t为预报时效,将t时效的高分辨率的精细化初估场(F500)与起报时刻的降尺度矢量DV作差,即可得到t时效下精细化的降尺度预报值DF,本文的预报时效t分别取1、2、3 d。

1.2.4自适应参数w的获取

通过IDS插值获取初估场后,利用公式(1)和(2),采用偏差“冷启动”方式估计插值偏差,进行降尺度预报。

图3给出了对w进行敏感性试验后,所得预报误差的均方根误差随w的变化趋势。发现,当w在0.4附近时,均方根误差达最小,也就是说此时预报试验的总误差最小;w向两端趋近时,均方根误差逐渐变大,尤其当w趋向于0时变化十分显著。最终,本文取w=0.43作为递减平均的自适应参数。

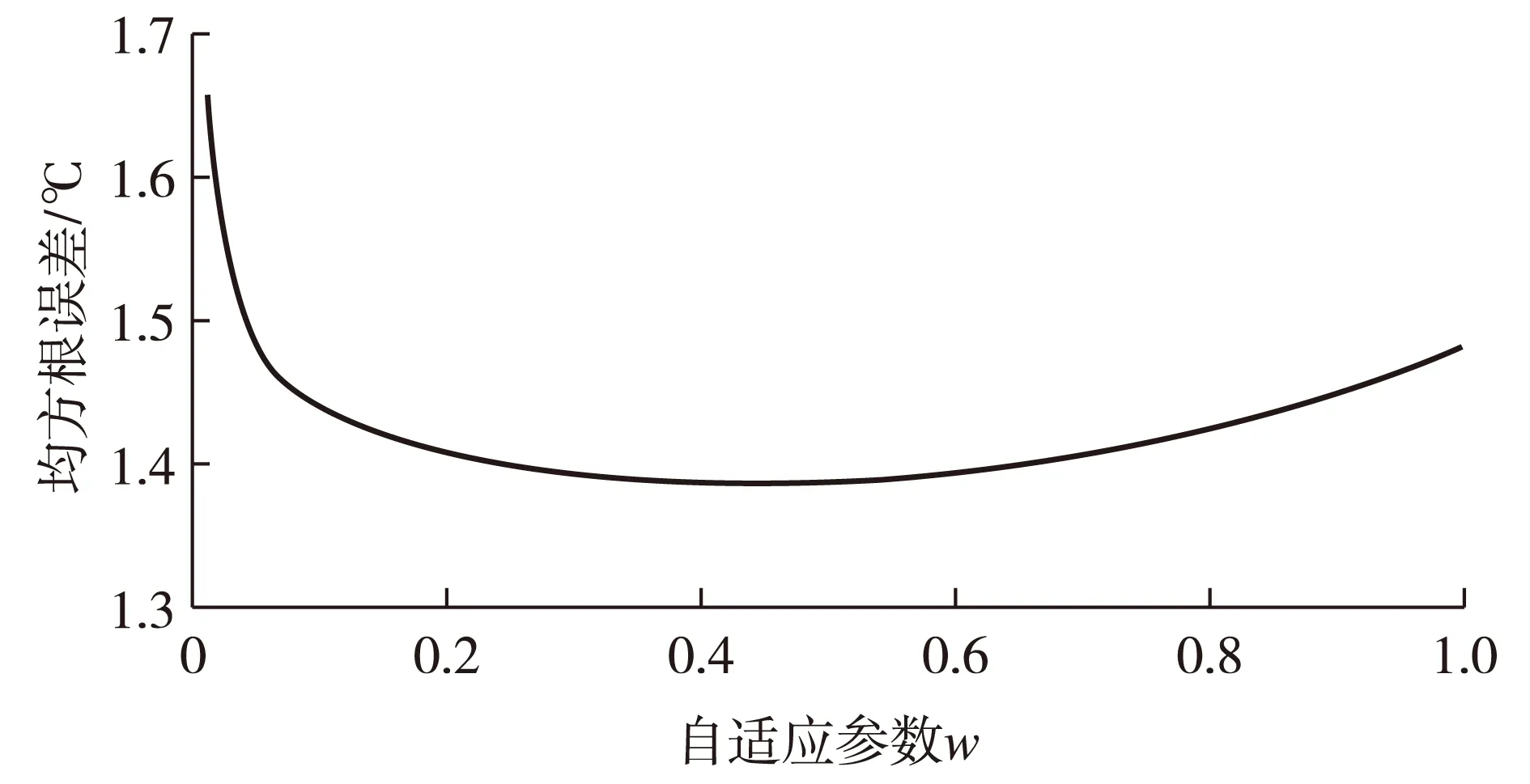
图3　不同自适应参数w下的精细化预报均方根误差Fig.3　RMSE of fine-scale forecasting with a different self-adapting parameter w

2　精细化预报效果分析

2.1全国预报误差随时效的变化

图4为预报误差的均方根误差随预报时效的变化以及与IDS插值均方根误差的比较。首先,关注均方根误差随时效的变化,它的基本变化趋势与业务预报一致:随着预报时效的增加,预报误差也在不断增大。1 d预报全年的均方根误差为1.4 ℃,2 d和3 d预报全年的均方根误差稍大,分别为1.6 ℃、1.7 ℃;并且,1 d预报与2 d预报之间的差异要大于2 d预报与3 d预报的差异。其次,经订正以后的预报与IDS插值结果相比,均方根误差均显著减小,尤其是1 d预报时年平均均方根误差减小了约1.5 ℃,减小幅度接近50%。

图4　不同预报时效下不同季节的预报均方根误差Fig.4　Forecasting RMSE in different seasons on different forecast days

2.2全国预报准确率

在精细化预报过程中,较为关注的是每日全国的预报能力,以预报误差的绝对值小于1.5 ℃作为预报准确的标准,计算平均每日全国预报准确的站数,并与IDS插值效果进行比较。

由图5可见,降尺度预报的效果与插值结果相比有很大的提高,前者预报准确率在70%～80%,而插值预报平均每日绝对误差小于1.5 ℃的站数在240站左右,准确率尚不足50%。降尺度预报使得平均每日预报准确的站数较插值预报提高了近100站,也就是使预报准确率提高了近20%,其中,在1 d预报情况下,预报准确率提高了30%之多。

图5　平均每日预报的绝对误差小于1.5 ℃的站数Fig.5　Daily number of stations whose absolute error was less than 1.5 ℃

2.3预报误差的时空变化

我国是一个气候多变、地形复杂的国家,不同的地区插值效果必然有所差异,那么全国各地的降尺度预报效果,以及递减平均法究竟在不同的地区有多大订正效果。

图6　降尺度预报和IDS插值的均方根误差的空间分布(单位:℃)　　a.IDS插值;b.1 d预报;c.2 d预报;d.3 d预报Fig.6　Distribution of the RMSE of fine-scale forecasting and IDS interpolation:(a)IDS;(b)1 d forecast;(c)2 d forecast;(d)3 d forecast

图6为降尺度预报和IDS插值的均方根误差的空间分布。总结四幅图的共同特征可知,预报误差的基本趋势是从东南地区向西北地区逐渐变大。均方根误差在西南和西北的山区为一个明显的大值区,而我国东南部和东北地区则是一个相对的小值区。这主要是由于北方边疆和西部地区相对复杂的地形和稀疏的站点分布,使得插值过程中产生了较大的误差,所设计的降尺度方案很难完全对该类地区进行订正。

对比图6a、b、c、d发现,图6a中,IDS插值的误差较大,全国的均方根误差普遍高于2 ℃,部分中西部地区甚至超过了4 ℃。将图6b、c、d与图6a比较可以发现,经过递减平均技术订正的降尺度预报的误差显著减小。原本误差较大的西部地区,经订正以后均方根误差平均减小了2 ℃,部分误差的高值中心已消失;原本误差相对较小的东南部地区预报状况也有所改善。整体而言,递减平均统计降尺度技术对初估场的订正是相当有效的,不但普遍减小了全国的预报误差,而且很大程度上改善了东西部预报效果“不平衡”的现象。

从上述分析可以发现,不同地区的预报效果存在着较大差异,以下根据预报的误差特征将我国简单的分为4个区域,对不同地区进行误差分析,研究偏差订正的改进效果。本文以35°N纬线和105°E经线为界,将我国分为东北、东南、西北、西南4个地区。

图7为预报时效为1 d时不同地区预报误差的均方根误差随时间的变化。整体而言,预报的均方根误差在冬季最大(平均为1.6 ℃),春季次之,夏季最小(平均为1.2 ℃),也就是说夏季的预报效果最好,而冬季最差。这主要是由于春、冬季节地面日平均温度波动较大,增加了偏差估计的难度,使得计算的降尺度矢量DV不能很好地代表系统偏差,从而导致春、冬季节精细化预报产生较大的误差。相反,夏季温度相对稳定、波动小,通过递减平均估算的偏差较准确,对初估场产生了较好的订正。对不同季节而言,春季4个地区的预报效果差异较小,均方根误差在0.3 ℃以内;从夏季开始,差异逐渐变大,到冬季东南地区和西北地区相差近0.7 ℃。也就是说,在不同季节,不同地区的预报能力有所差异。并且对不同区域而言,东南地区始终是预报效果最好的(均方根误差为1.2 ℃),向西北方向预报效果逐渐变差,并且预报效果的季节差异也相应不断增加。

图7　1 d预报的均方根误差的时空变化Fig.7　Spatiotemporal variation of 1 d forecast RMSE

从图8可以看出,相同时效下,东南地区的预报准确率始终高于其他地区,其中1 d预报时准确率高达85%;东北和西南地区的效果比较接近,3 d内预报准确率均介于70%～80%;西北地区的预报效果始终是最差的。1 d预报和3 d预报相比,不同地区的预报准确率均高出10%以上,其中东南部地区二者的差异最大。降尺度预报和IDS插值结果相比,预报准确率的提高十分显著。以3 d预报为例,东南地区提高的幅度最小,为10%;西北地区的准确率提高幅度最大,接近30%。也就是插值准确率越低的地区改进的幅度越大,使得降尺度以后预报效果的空间差异显著减小。

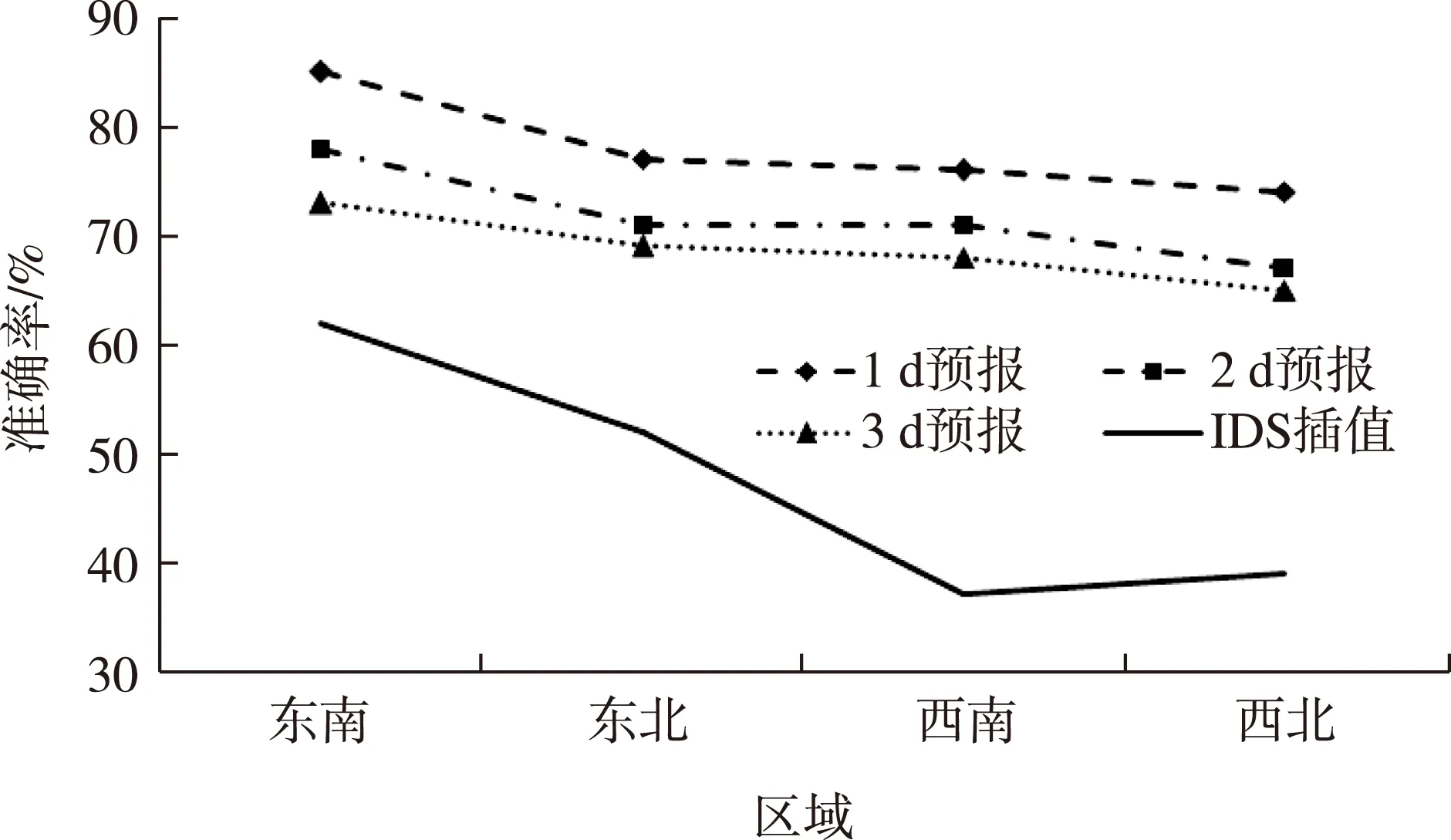
图8　不同时效下不同区域预报准确率Fig.8　Forecasting accuracy in different regions on different forecast days

由上述分析可见,递减平均统计降尺度技术具有较强的精细化预报能力,降尺度矢量DV的构建是成功的,很好地订正了插值误差。

3　结论

本文利用中国600个基本、基准地面气象观测站2000—2010年地面日平均气温数据构建“预报场”和“分析场”,采用具有自适应特征的Kalman滤波类型的递减平均统计降尺度技术,对中国地面温度进行精细化预报,对预报效果进行了评估,并与IDS插值结果进行了比较,得如下结论:

1)递减平均统计降尺度技术对中国地面温度进行精细化预报是可行的。精细化预报的误差从东南向西北增大,预报能力夏、秋、春、冬依次减弱,且随着预报时效的增加预报准确率逐渐降低。3 d内预报的均方根误差在1.4～1.7 ℃,预报准确率在70%～80%,基本满足业务要求,适合在基层台站推广。

2)距离平方反比权重插值(IDS)可提供误差较小的初估场,其操作简单易行。自适应的偏差订正降尺度方案相比上述插值方法有明显的提高,最关键的降尺度矢量DV构建合理,很好地估计了插值产生的精细化初估场的偏差。3 d内预报的均方根误差平均减小1.4 ℃、预报准确率提高20%～30%,尤其对插值误差较大的西部地区产生了很好的订正,预报准确率的提高幅度超过30%,有效地改善了西部的预报效果,使预报能力的空间差异显著减小。

参考文献(References)

Anandhi A,Srinivas V V,Kumar D N,et al.,2009.Role of predictors in downscaling surface temperature to river basin in India for IPCC SRES scenarios using support vector machine[J].Int J Climatol,29(4):583-603.

Cui B,Toth Z,Zhu Y J,2011.Bias correction for global ensemble forecast[J].Wea Forecasting,27:396-410.

钞振华,2011.三种再分析气温资料在中国西部地区的可信度评价[J].大气科学学报,34(2):162-169.Chao Z H,2011.The reliability evaluation of three types of air temperature reanalysis data in West China[J].Trans Atmos Sci,34(2):162-169.(in Chinese).

陈威霖,江志红,黄强,2012.基于统计降尺度模型的江淮流域极端气候的模拟与预估[J].大气科学学报,35(5):578-590.Chen W L,Jiang H,Huang Q,2012.Projection and simulation of climate extremes over the Yangtze and Huaihe River Basins based on a Statistical Downscaling Model[J].Trans Atmos Sci,35(5):578-590.(in Chinese).

陈豫英,陈晓光,马金仁,等,2005.基于MM5模式的精细化MOS温度预报[J].干旱气象,2(4):52-56.Chen Y Y,Chen X G,.Ma J R,et al.,2005.Fine MOS temperature forecast based on MM5[J].Arid Meteorology,2(4):52-56.(in Chinese).

Engel C,Ebert E E,2011.Gridded operational consensus forecasts of 2-m temperature over Australia[J].Wea Forecasting,27:301-322.

范丽军,符淙斌,陈德亮,2007.统计降尺度法对华北地区未来区域气温变化情景的预估[J].大气科学,131(15):887-897.Fan L J,Fu Z B,Chen D L,2007.Estimation of local temperature change scenarios in North China using statistical downscaling method[J].Chin J Atmos Sci,131(15):887-897.(in Chinese).

郭虎,杨建捷,杨波,等,2008.北京奥运演练精细化预报方法及其检验评估[J].气象,6(34):17-25.Guo H,Yang J J,Yang B,et al.,2008.Refined forecast techniques and related verification during 2007 Olympic Drilling[J].Meteor Mon,6(34):17-25.(in Chinese).

Huth R,Kliegrova S,Metelka L,2008.Non-linearity in statistical downscaling:Does it bring an improvement for daily temperature in Europe[J].Int J Climatol,28(4):465-477.

贾小龙,陈丽娟,李维京,等,2010.Bp-cca方法用于中国冬季温度和降水的可预报性研究和降尺度季节预测[J].气象学报,68(3):398-410.Jia X L,Chen L J,Li W J,et al.,2010.Statistical downscaling based on BP-CCA:Predictability and application to the winter temperature and precipitation in China[J].Acta Meteorologica Sinica,68(3):398-410.(in Chinese).

Kidnson J W,Thompson C C,1998.A comparison of statistical and model-based downscaling techniques for estimating local climate variations[J].American Meteorological Society,4(11):735-753.

Lam N S,1983.Spatial interpolation method:A review[J].The American Cartographer,10:129-149.

李江萍,王式功,2008.统计降尺度在数值预报产品使用中的应用[J].气象,34(6):41-45.Li J P,Wang S G,2008.Application of statistical downscaling method to numerical weather forecast[J].Meteor Mon,34(6):41-45.(in Chinese).

李莉,李应林,田华,等,2011.T213全球集合预报系统性误差订正研究[J].气象,37(1):31-38.Li L,Li Y L,Tian H,et al.,2011.Study of bias-correction in T213 global ensemble forecast[J].Meteor Mon,37(1):31-38.(in Chinese).

李新,程国栋,卢玲,2000.空间内插方法的比较[J].地球科学进展,25(13):261-265.Li X,Cheng G D,Lu L,2000.Comparison of spatial interpolation mrthods[J].Advances in Earth Science,25(13):261-265.(in Chinese).

Lian S M,Wang K,Cui M C,et al.,2010.Exercise in downscaling on sea surface temperature along Chinese coast[J].Chinese Journal of Oceanology and Limnology,18(2):110-116.

林忠辉,莫兴国,李宏轩,等,2002.中国陆地区域气象要素的空间插值[J].地理学报,27(1):47-56.Lin Z H,Mo X G,Li H X,et al.,2002.Comparison of three spatial interpolation methods for climate variables in China[J].Acta Geographical Sinica,27(1):47-56.(in Chinese).

刘永和,郭维栋,冯锦明,等,2011.气象资料的统计降尺度方法综述[J].地球科学进展,26(8):837-847.Liu Y H,Guo W D,Feng J M,et al.,2011.A summary of methods for statistical downscaling of meteorological data[J].Advances in Earth Science,26(8):837-847.(in Chinese).

Mearns L O,Bogardi I,Giorgi F,et al.,1999.Comparison of climate change scenarios generated from regional climate model experiments and statistical downscaling[J].J Geophys Res,3(104):6604-6621.

Monache L D,Nipen T,Liu Y B,et al.,2011.Kalman filter and analog schemes to post-process numerical weather predictions[J].Mon Wea Rev,139:3354-3570.

Mpelasoka F S,Mullan A B,Heerdegen R G,2001.New Zealand climate change information derived by multivariate statistical and artificial neural networks approaches[J].Int J Climatol,21:1415-1433.

Oshima N,Hisashi K,Shinji K,2002.An application of statistical downscaling to estimate surface air temperature in Japan[J].J Geophys Res,107(D10):1401-1410.

彭彬,周艳莲,高苹,等,2011.气温插值中不同空间插值方法的适用性分析—以江苏为例[J].地球信息科学学报,13(4):539-547.Peng B,Zhou Y L,Gao P,et al.,2011.Suitability assessment of different interpolation methods in the gridding process of station collected air temperature:A case study in Jiangsu province,China[J].Geo-Information Science,13(4):539-547.(in Chinese).

王辉赞,张韧,王彦磊,等,2006.基于Kalman滤波的副热带高压数值预报误差修正[J].热带气象学报,22(6):661-666.Wang Z H,Zhang R,Wang Y L,et al.,2006.Errors revised for numerical forecast products of subtropical high based on Kalman filtering[J].J Trop Meteor,22(6):661-666.(in Chinese).

徐振亚,任福民,杨修群,等,2012.日最高温度统计降尺度方法的比较研究[J].气象科学,32(4):395-402.Xu Z Y,Ren F M,Yang X Q,et al.,2012.A comparison study on statistical downscaling methods in daily maximum temperatures[J].J Meteor Sci,32(4):395-402.(in Chinese).

智协飞,季晓东,张璟,等,2013.基于TIGGE资料的地面气温和降水的多模式集成预报[J].大气科学学报,36(3):257-266.Zhi X F,Ji X D,Zhang J,et al.,2013.Multimodel ensemble forecasts of surface air temperature and precipitation using TIGGE datasets[J].Trans Atmos Sci,36(3):257-266.(in Chinese).

The statistical downscaling technique based on large-scale numerical forecasting productions is an effective method for fine-scale forecasting.In China,researchers use interpolation methods such as bilinear interpolation and inverse distance interpolation to produce a downscaled forecast.In recent years,the Kalman filter—type self-adapting decaying average downscaling technique has been designed overseas for forecast downscaling,which is better than the MOS method.Based on a daily surface temperature dataset of 752 weather stations for the period 2000 to 2010 in China,a fine-scale prediction test with a low-resolution “forecast field” and fine-scale “analysis field” for daily average temperature,using the self-adapting Kalman Filter—type decaying average statistical downscaling technique,was designed,without the effect of forecasting error in numerical forecasting production.The result of the downscaled prediction was compared with the interpolation method and analyzed for its possibility of application in China.

The decaying average technique in this paper filtered the observational data in order and determined the change of the dynamic system constantly.Then,systematic bias(called the “downscaling vector”,DV) was estimated.Finally,the prediction outcome was then corrected by the bias.This was a kind of self-adapting bias-estimated method,similar to the Kalman filter and a statistical post-processing method.The DV,defined as the difference between the “forecast field” and “analysis field” at the same time,presents the statistical relationship and systematic bias between the forecast and analysis.The DV that is weight-averaged between the last DV and the forecast error at the same time is updated by the decaying average algorithm.Thus,we can extract error information between the forecast and the observational data to estimate the forecast bias.The result show that:

(1)The 1—3 d forecast accuracy rate of the self-adapting Kalman filter—type decaying average statistical downscaling technique was 70%—80%,which is basically satisfactory for professional application.The RMSE of the 1—3 d forecasts was between 1.4 ℃ to 1.7 ℃,and the average value in China was 1.5 ℃.The error increased from Southeast China(RMSE of 1.4 ℃) to Northwest China(RMSE of 1.8 ℃).The forecasting ability decreased with the increase of the forecast limitation.The forecast effect was best in summer and worst in winter.

(2)The IDS interpolation method was able to provide the best estimated field,but the decaying average statistical downscaling technique was better than any interpolation method.The critical DV was structured reasonably,able to estimate the interpolation bias of the estimated field well.The RMSE decreased to 50% on average(approximately 1.4 ℃),and the forecast accuracy rate increased by 20%—30% in the 1—3 d forecasts.In particular,the large gap in forecasting ability between West China and East China was reduced,and the accuracy rate increased more than 30% in West China,where there was a large error.

In conclusion,the forecasting ability of the method was verified by producing a low-resolution “forecast field” and fine-scale “analysis field” without the influence of forecasting error in the numerical forecasting product.Therefore,the decaying average statistical downscaling technique is feasible for operational fine-scale surface temperature forecasting in China.

In future work,we intend to combine numerical forecasting products and reanalysis temperature data to generate a realistic prediction test for demonstrating how the Kalman filter—type self-adapting decaying average downscaling technique performs.

fine-scale forecasting;statistical downscaling;interpolation;decaying average algorithm

(责任编辑：刘菲)

doi：10.13878/j.cnki.dqkxxb.20130206001

Surface temperature statistical forecasting downscaling research in China

CHEN Guohua,GUO Pinwen

MeteorologicalDisaster,MinistryofEducation(KLME),NanjingUniversityofInformationScience&Technology,Nanjing210044,China

引用格式：陈国华,郭品文,2016.中国地面气温统计降尺度预报方法研究[J].大气科学学报,39(4):569-575.

Chen G H,Guo P W,2016.Surface temperature statistical forecasting downscaling research in China[J].Trans Atmos Sci,39(4):569-575.doi：10.13878/j.cnki.dqkxxb.20130206001.(in Chinese).

*联系人，E-mail:glory_1999@163.com