基于分数阶傅里叶变换的滤波*

步衍瀚　王平波

(海军工程大学　武汉　430033)



基于分数阶傅里叶变换的滤波*

步衍瀚王平波

(海军工程大学武汉430033)

摘要分数阶傅里叶变换是一种较好的滤波处理工具。利用分数阶傅里叶变换进行滤波处理是基于时频平面旋转的信号滤波方法，即将信号在时频平面上旋转特定的角度，使得信号在新的时频平面上退化为单频正弦信号。基本思路是利用分数阶傅里叶变换对信号进行旋转分离，从而达到抑制噪声的目的。分离出的信号通过对时频平面的反向旋转，恢复出原信号。通过对算法的分析论证，分数阶傅里叶域滤波算法性能优于其他滤波算法。仿真结果表明，该方法不仅效果明显，而且信号失真小。和其它滤波算法相比，计算复杂度低更容易实现。

关键词分数阶傅里叶变换； 信号处理； 滤波

Class NumberTN911

1　引言

对于从事信号处理方面研究的工作者来说，滤波是一个非常重要的环节。在实际应用中，经过各种信道传输后，传播的信号将不可避免地混有噪声[1]。从时频域上分析，经典的滤波方法大都只是从时域或频域上入手进行信号分离，但由于很多信号是宽带信号，在时频域上都有较强的耦合，使得经典的滤波方法难以实现有效的滤波[2]。

近年来，被广泛应用于信号处理领域的一种工具——分数阶傅里叶变换(Fractional Fourier Transform，FRFT)，成为滤波处理的一种实用好用的方法[3]。目前随着对分数阶傅里叶变换的深入研究，基于分数阶傅里叶域的滤波技术日趋成熟。下文中将对分数阶傅里叶域与传统的时频域做一个形象的论述，对于初次接触分数阶傅里叶变换的研究者来说会有所帮助。

从分数阶傅里叶域与时域频域之间的关系来看分数阶傅里叶变换实质上是一种统一的时频变换[3]，同时反映了信号在时域、频域的信息。它和常用的二次型时频分布不同的是，分数阶傅里叶变换用单一变量表示时频信息且没有交叉项。与传统傅里叶变换相比，分数阶傅里叶变换更适合处理非平稳信号，尤其是线性调频信号[4]。利用线性调频信号在不同阶数分数阶傅里叶域呈现不同的能量聚集特性，通过对分数阶傅里叶域进行峰值二维搜索，就可以实现对LFM信号的检测和参数估计[5]。基于此本文做出这方面的仿真实验与传统傅里叶变换滤波做了对比，可以很好的看出滤波效果更好。

2　分数阶傅里叶变换的基本定义

2.1分数阶傅里叶变换定义

作为傅里叶变换的广义形式，p阶傅里叶变换可以看做信号在时频域上坐标轴绕原点逆时针旋转pπ/2角度后构成的分数阶傅里叶域上的表示[6]。当旋转角度为π/2时即为傅里叶变换。如图1所示。

图1　分数阶Fourier域(u，v)

在t域的函数x(t)的p阶分数阶傅里叶变换的定义为

(1)

(2)

(3)

其中p≠2n。

分数阶傅里叶变换的逆变换为

(4)

2.2从时域和频域到分数阶傅里叶域

下面用直观的表述方法来分析分数阶傅里叶变换，对初接触这一领域的研究人员来说更易理解。信号可以展开成n组正弦波的叠加[7]，其时域频域图像如图2。

传统傅里叶变换从时域旋转π/2角度后到频域的变换。结合图2和图1，p阶傅里叶变换就是时频域旋转角度为pπ/2构成的新的(u，v)域。

2.3分数阶傅里叶变换的性质

分数阶傅里叶变换的基本性质有线性、酉性、阶数可加性、交换性、结合性等。其中一个重要性质是阶数可加性(又称旋转可加性)，如0.3阶分数阶傅里叶变换的0.5阶变换是0.8阶变换。而p阶的-p阶变换即为原信号。基于此我们在p阶分数阶傅里叶域做完滤波处理再进行-p阶变换，得到的便是滤波后的信号。

图2　时域和频域(t,ω)

2.4信号的分数阶傅里叶变换分布图

设一初始频率为100Hz，截止频率为200Hz，脉宽0.1s的线性调频信号。经分数阶傅里叶变换Matlab仿真，该信号在分数阶域上的分布如图3所示。

图3　信号在分数阶傅里叶域上的分布

其中采样频率为1000Hz，采样点取100，当p=0.83时信号能量聚集最大。

3　分数阶傅里叶域滤波原理和步骤

以线性调频(LFM)信号为例，设被观测信号为混有加性高斯白噪声的LFM信号。其表示为

x(t)=s(t)+ω(t)

=a0exp(jπm0t2+j2πf0)+ω(t)

(5)

其中a0,m0,f0为未知参数，ω(t)为加性高斯白噪声。a0为其包络函数，m0是线性调频率，f0为初始频率。滤波算法的第一步是进行参数估计，检测含有未知参数的LFM信号基本思路是以旋转角α为变量做二维扫描，形成(a,u)二维平面，在此平面上对各峰值做遮隔处理。其检测和估计过程可以描述为

(6)

其中：

(7)

虽然检测方法看上去较为直观，但实际操作起来会面临着一些问题：比如当参数精度要求较高时，必须选择较小步长，这会大大增加运算量及计算的复杂程度。文献[8]中给出了一种两级搜索的方法。首先对观测信号选用大的搜索步长，采用较低的分辨率进行直接搜索对参数进行粗略估计；然后以这一估计值为初始值利用拟牛顿法进行迭代搜索，得到精确估计。其过程为

(8)

其选取的p阶分数阶傅里叶域要遵循两个原则：一是信号要有很好的聚集性，二是信号和噪声尽量没有耦合。

在得到参数估计之后，滤波算法的步骤如下：

1) 对信号进行p阶FPFT，得到旋转角度α0=pπ/2后信号表示为

Xp(u)=Sp(u)+Np(u)

(9)

其中Sp(u)为信号的分数阶傅里叶变换，Np(u)为噪声的分数阶傅里叶变换。在u域上Np(u)一般不会出现聚集特性。

2)在u域上进行尖峰遮隔处理：

=Sp(u)Mp(u)+Np(u)Mp(u)

(10)

其中Mp(u)是中心频率为u0的带通滤波器。选择适当的带宽可以有效滤除大部分噪声能量。但由于带宽越大信号两端越平滑，较大带宽滤波会形成一个钟形脉冲。因此对等幅信号进行滤波要想较好还原波形，带宽选择不宜过大。

3)对处理结果进行p阶反变换，便可得到滤波后的原信号。

4　仿真结果

设信号是一个混有均值为零的加性高斯白噪声的单分量线性调频信号，信噪比为-3dB。图4(a)为原信号波形，图4(b)给出了叠加噪声后的波形。滤波过程如下：首先，对叠加信号在(a,u)平面进行二维搜索，搜索范围p=0～2(p=2α/π)，搜索步长(间隔)0.01。得到峰值点p0=1.63和u0=279，(a，u)平面上其幅值分布如图4(c)。然后，对叠加信号做1.63阶FRFT变换，在u域上进行窄带通滤波(尖峰遮隔)，滤波前后u域幅值如图4(d)、图4(e)。最后，将滤波后的信号做1.63阶的反变换，还原到时域波形便得到了除噪后的信号，见图4(f)。

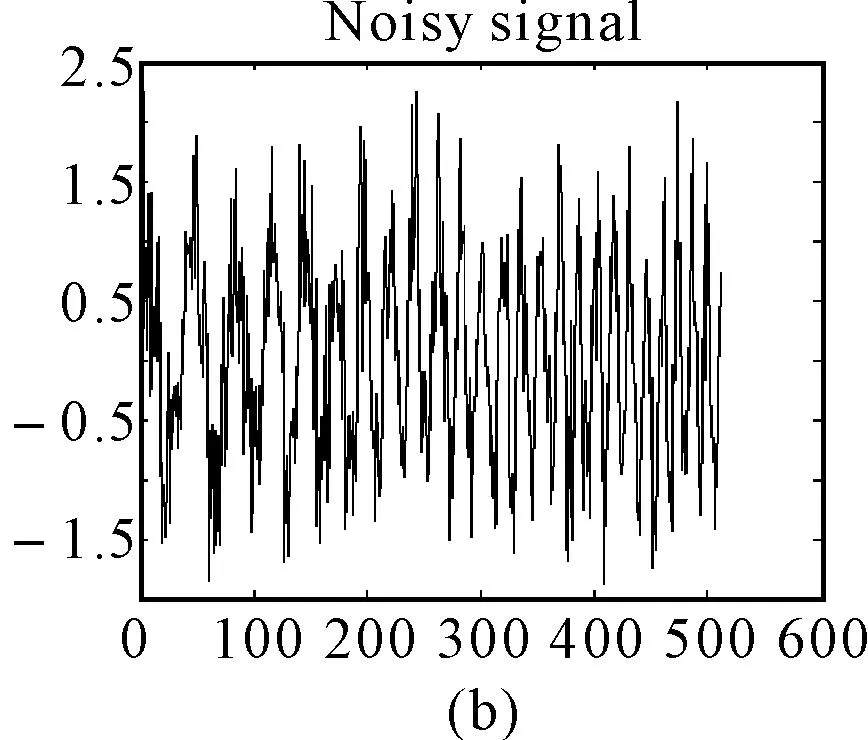
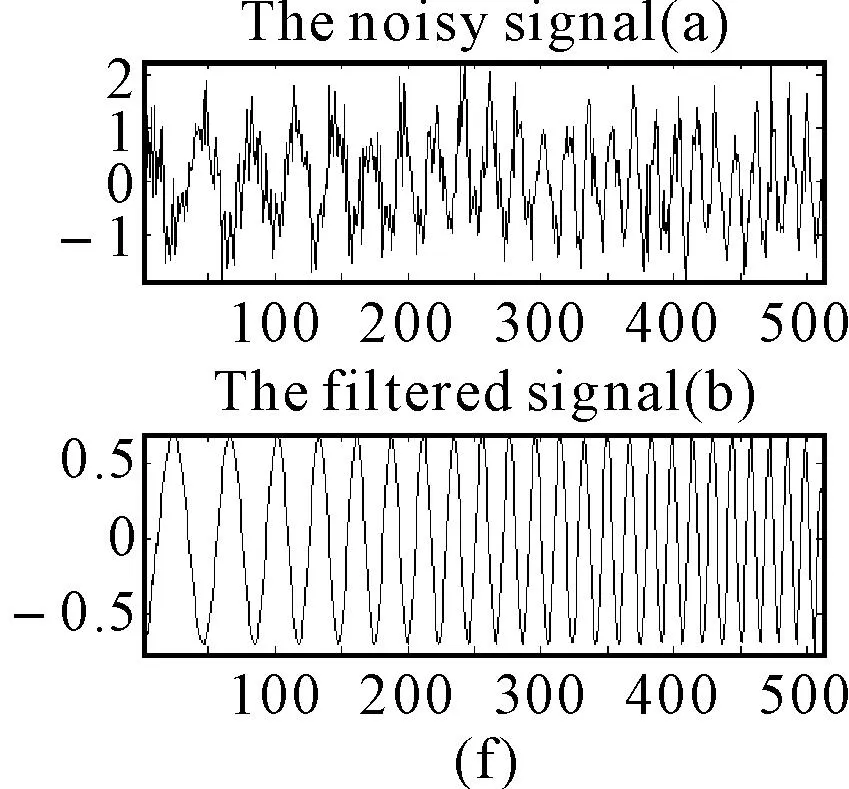
图4　分数阶傅里叶域滤波处理

对比图4(f)和图4(a)，可以看出由于噪声影响及滤波处理，还原的信号和原信号有一定的相位差，但这不影响信号中包含的信息：LFM信号的信息量在包含频率中。

5　结语

分数阶傅里叶变换和其他时频分析方法相比，计算量和复杂程度更低，实现起来更为简便[10]。分数阶傅里叶域滤波也可以说是一种最优滤波方法，相对于其他方法设计相对简单。本文介绍了分数阶傅里叶变换的基本概念以及对LFM信号的滤波方法，其基本思路是利用分数阶傅里叶变换对信

号进行旋转分离，从而达到抑制噪声的目的。通过本文提出的方法可以有效进行单分量LFM信号的滤波处理。另外本文直观形象地用立体图对比表述了时域频域和分数阶傅里叶变换的关系，对初学者而言更容易理解和入门。通过仿真对比，本文提出的方法步骤简单明了，易于操作实现。

参 考 文 献

[1] 惠俊英，生雪莉.水下声信道[M].北京：国防大学出版社，2007.

[2] 吴正国，夏利，尹为民.现代信号处理技术[M].武汉：武汉大学出版社，2003.

[3] 陈小龙，关键，刘宁波,等.基于FRFT的LFM信号自适应滤波算法及分析[J].南京：现代雷达，2010，32(12)：54-59.

[4] H. M. Ozakatas, O. Arikan, et al. Digiita Computation of the Fractional Fourier Transform[J]. IEEE Trans.Signal Processing，1996，44(9)：2141-2150.

[5] 陶然，邓兵，王越.分数阶傅里叶变换及其应用[M].北京：清华大学出版社，2009.

[6] 刘建成，刘忠，王雪松.高斯白噪声背景下的LFM信号的分数阶Fourier域信噪比分析[J].北京：电子与信息学报，2007，29(10)：2337-2340.

[7] Ahmed Zzyed. On the relationship between the Fourier and fractional Fouriertransform[J]. IEEE， SPLetters，1996，3(12):310-311.

[8] 齐林，陶然，周思永,等.基于分数阶傅里叶变换的线性调频信号的自适应滤波[J].北京：兵工学报，2003，24(4)：499-503.

[9] QI Lin, TAO Ran, ZHOU Siyong. Detectionand pa-rameter estimation ofmulticomponent LFM signal based on the fractional Fourier trans-form[J]. Sciencein China Ser. F Information Sciences，2004，47(2)：184-198.

[10] 李靖，王树勋，汪飞.基于分数阶傅里叶变换的chirp信号时频分析[J].北京：系统工程与电子技术，2005，27(6)：988-990，1015.

*收稿日期：2015年10月28日,修回日期：2015年11月10日

基金项目：国家自然科学基金(编号:4355163606)资助。

作者简介：步衍瀚，男，硕士研究生，研究方向：水声信号处理。王平波，男，博士，教授，博士生导师，研究方向：水声信号处理。

中图分类号TN911

DOI：10.3969/j.issn.1672-9730.2016.04.010

Filtering Based on Fractional Fourier Transform

BU YanhanWANG Pingbo

(Naval University of Engineering, Wuhan430033)

AbstractFRFT(Fractional Fourier Transform) is a good filtering processing tool. Using FRFT to process the signal is a signal filtering method that based on the time-frequency plane rotary. From the signal in the time-frequency plane rotation specific angle, the signal is made degradation in the new time-frequency planefor single frequencysine signal to do processing, making signal-noise separation. A reverse rotation recovers the singal without noise. Through the argumentation and the simulation results, this method not only has obvious offect but also is simple, and has small amount of calculation. Compared with other fiteringalgorithm, this algorithm has low computation and is easy to implement.

Key Wordsfractional fourier transform, signal processing, filter