密立根与电子电荷的测量
2016-08-11刘艳莉
刘艳莉
1923年12月10日,瑞典斯德哥尔摩金碧辉煌的音乐大厅里灯光耀眼、鲜花芬芳,乐曲声中,中年科学家罗伯特·安德鲁斯·密立根(R.A.Millikan)稳步登上领奖台,领取了物理学的最高荣誉——诺贝尔物理学奖,成为当时美国最著名的物理学家之一。
一、毕生追求科学真理
密立根1868年3月出生于美国伊利诺伊州的莫里森。父亲是公理教会的传教士,母亲毕业于奥伯林学院,曾任密歇根州奥利瓦特学院的院长,密立根的童年时光是在艾奥瓦州的马可达度过的。1886年,密立根进入奥伯林学院预科学习,二年级结束时,学校便邀请他担任初级物理课的老师。他非常喜欢这个工作,不久就决定把它作为自己的终身职业。
1891年,密立根从奥伯林学院毕业后,一面继续物理课的教学,一面进修电动力学,并于1893年获硕士学位,同年进入哥伦比亚大学物理系学习,成为学校里唯一的物理学研究生。1894年夏,密立根又进入芝加哥大学,在迈克尔逊(A.A.Michelson)指导下学习实验技术。1895年获博士学位后,赴欧洲游学。1896年,密立根回到芝加哥大学担任物理学助教。1907年,由于教学上的成绩被提升为副教授。
密立根于1909年起开始测量电子电荷。经过上千次实验,他最终得到了较为精确的电子电荷的数值为1.6×10ˉ19库。这一结果有力地证明了电子是具有一定电荷和质量的基本微粒,并使我们能以较高的精确度计算的重要的物理常数。
同时在1912~1915年间,密立根利用复杂、精密的仪器和处于高真空中的样品,检验了爱因斯坦1905年提出的光电效应关系。当入射光的频率为ν的情况下,他测量了遏止电子从金属中逸出所需要的最小电压Us。验证了爱因斯坦方程Ek=Use=hν-W,并首次对普朗克常量h直接运用光电学方法做了测定。
就是因为对电子电荷的测量和光电效应的研究,密立根获得了1923年的诺贝尔物理学奖。
1953年12月19日,密立根在加利福尼亚的帕萨登那逝世,享年86岁,密立根对物理学的发展与进步有着卓越的贡献。
二、密立根对电子电荷测量的贡献
1909年,密立根开始埋头于电子电荷的测量工作。电子是非常小的微观粒子,它所携带的电荷更是微乎其微,因此测量电子电荷是非常困难的工作。当时还没有人对电子电荷得到可靠准确的数值。一些反对原子学说的人坚持认为这并不是一个独特的粒子常数,而是大小不同的电荷能量的统计平均值。
在英国物理学家威尔逊(H.A.Wilson)发明云室后(称威尔逊云室:让带电粒子射入压力很低、装有潮湿空气的容器中,云雾就接连的在运动粒子周围凝结,显示出清晰的粒子轨迹),另一位英国著名物理学家汤姆逊(J.J.Thomson,1906年诺贝尔物理学奖获得者,电子的发现者),便在英国剑桥大学的卡文迪许实验室,利用威尔逊云室测量电子的电荷“e”。但他测量得的e值为1.03×10ˉ19C。1903年威尔逊也利用自己发明的云室进行了测量,测得的结果为0.67×10-19~1.47×10-19C,其平均值和汤姆逊测量的e值差不多,但误差都比较大。
密立根也采用了威尔逊云室来进行实验,即在平行板电容器之间形成水蒸气凝成的云雾,首先测量水蒸气带电云在重力场的影响下的降落速率,再加适当的反向电场力,使之与重力平衡,就可以计算出带电云的电量。
但密立根很快就认识到这种方法中包含许多不确定因素,如云表面的蒸发会影响下落速率的测量。为了修正这一影响,密立根决定采用强电场使云雾维持在固定位置来研究蒸发过程。然而,当加上强电场后,云雾就消散了,只留下少数几个带电水滴在外加电场和重力场作用下缓慢移动。密立根立刻意识到,用单个水滴来测定电子电荷比用大片雾粒精确得多。他发现大的水滴可以在长达45秒钟的时间内不被蒸发掉。几个月的时间内,他测得的结果表明:任一给定水滴上的电荷总是一个不可约值的整数倍。
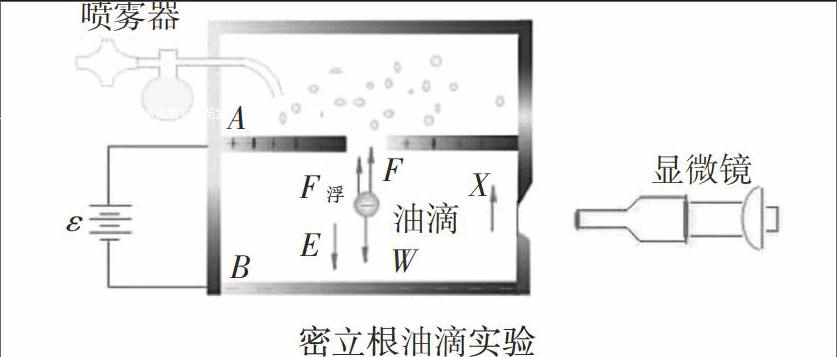
1909年冬,密立根用油滴代替水滴,从而大大改进了测量方法。因为油滴挥发得很慢,可以跟踪观察一个油滴长达4小时之久。另外,他用镭的射线(即α射线)射到油滴室里使空气电离,油滴在不时地捕捉电子,就可以任意改变油滴的电荷。油滴在电容器两极板间由于电场力的变化而运动。他的所有结果都确切地证实了油滴上的电荷是一个最小值的整数倍。这就是著名的密立根油滴实验。
实验装置如上图所示。油滴从喷雾器喷出,并通过平板
上的小孔落到两个水平放置的平行板之间的空间。由于喷嘴处的摩擦作用,或油滴受到α射线、γ射线等的作用,都会使得一些油滴带电。设一油滴所带电荷为-q,如果两极板间没有电压,极板间就没有电场,则油滴只在重力作用下加速下落。在下落过程中,油滴速率逐渐增加,此时它除受重力作用外,还受流体(空气)的阻力作用,阻力方向竖直向上,因此油滴很快以恒定的终极速率υ1下落。终极速率依赖于油滴的尺寸。如以G代表油滴所受重力,Fr代表油滴在空气中所受阻力,当无外电场作用,且油滴达到终极速率时有G=Fr,其中Fr=6πηrυ1,称斯托克斯公式,r为油滴半径,η为气体的黏滞系数,如以m代表油滴质量,于是有
