具有参数漂移特征的产品可靠度分布规律研究*

翟亚利　张志华　宋　祁

(海军工程大学　武汉　430033)



具有参数漂移特征的产品可靠度分布规律研究*

翟亚利张志华宋祁

(海军工程大学武汉430033)

摘要对具有参数漂移特征的产品可靠性服从的规律进行了研究,分析了常见分布(指数分布、正态分布、对数正态分布、三参数威布尔分布、伽马分布)的特点和参数估计方法,从获得的产品可靠度值的范围不同的角度,分三种情形进行可靠度曲线拟合分析,仿真结果说明,当可以通过先验信息大概确定正态分布或对数正态分布参数的取值范围时,使用正态分布或对数正态分布拟合可靠度曲线效果较好,否则使用三参数威布尔分布效果较优。

关键词参数漂移; 可靠度分布规律; 参数估计

Class NumberO141.4

1引言

产品在使用过程中,通常需要进行定期监控,以确保其正常运行,在监控过程中得到的产品性能指标检测信息包含了大量的产品可靠性信息。利用产品检测信息,一方面可以及时判断产品当前运行状态,确定是否需要实施保障措施[1];另一方面,可以利用检测信息计算得到产品性能指标的变化趋势进而预测产品寿命,为预防性维修(或报废)时间的确定提供依据[2～3]。因此,充分利用产品定期检测信息确定性能指标的变化规律,进而预测产品寿命,成为近年来产品可靠性研究的重要方向。

具有参数漂移特征的产品的可靠性评估是通过分析产品的性能指标退化机理,建立产品性能指标退化与其可靠性之间的数学模型,进而预测其剩余寿命。文献[4～5]利用退化量的散布特征将各个时刻产品性能指标的退化信息转化为该时刻产品的可靠性信息,利用产品可靠性寿命分布拟合产品可靠性规律,实现产品可靠性评估。该评估方法充分利用了产品的寿命分布信息,其可靠性评估结果具有较好的鲁棒性,尤其是在产品退化观测数据较多的情况下,可以较准确地拟合产品寿命分布。文献[6]基于随机扩散理论,提出了将参数漂移模型预测与产品寿命分布拟合相结合的可靠性评估方法,提高了产品可靠性的评估精度。文献[4～8]中利用可靠性寿命分布对可靠性进行预测时,根据工程经验使用了三参数威布尔分布,但是并没有对寿命分布进行证明或仿真说明。

本文针对具有参数漂移特征的性能退化产品,以性能参数漂移模型为基础,分析了常见分布,即指数分布、正态分布、对数正态分布、三参数威布尔分布、Gamma分布的参数估计方法,进一步,通过仿真算例分析各种常见分布对参数漂移模型寿命分布的拟合程度。仿真结果说明,当可以大致估计寿命分布的均值和方差范围时正态分布的拟合效果最优,当没有任何先验信息时,三参数威布尔分布的拟合效果最优。

2参数漂移的退化可靠性模型

对于具有参数漂移特征的产品,其参数漂移行为常常可以用扩散过程近似描述。一般情况下,通常假定产品参数在初始时刻没有漂移(即漂移值为零),随着产品使用时间的延长,产品参数出现随机漂移,并逐步远离中心,其漂移偏离速度和波动幅度逐渐增加。当产品参数漂移量超出规定的上下限时,产品发生失效。

2.1模型假设和建立

根据工程实践经验,产品参数的漂移可解释为产品受到的各种外部随机冲击与内部失效因素的不断累积造成的,在产品质量与工作环境较为稳定的情况下,这些外部随机冲击和内部失效因素的累积主要与产品工作时间有关。

由文献[1]可知,在假设产品在时刻t的参数漂移量X(t)是独立增量过程,其在初始时刻的漂移量为0,即X(0)=0,且参数漂移量X(t)的漂移系数和扩散系数分别为常数a,b时,X服从正态分布N(at,b2t)。即

(1)

假设产品退化量从某时刻t0开始,其退化规律可以用参数漂移模型进行描述,且该时刻性能指标的退化量为X(t0)=x0,则X服从N(x0+a(t-t0),b2(t-t0))。

2.2产品退化可靠度

对于具有参数漂移特征的产品而言,当其退化量在一定范围内漂移时产品能够正常工作,否则,当产品的退化量超出其允许上下限时,产品处于失效状态。假设产品性能指标的允许上限为Xcu。产品退化量首次超出允许上限的时间即为产品失效时间。即

T(Xcu)=inf{t:X(t)=Xcu,t≥0}

则产品在任意时刻t的失效概率为

F(t)=P{T≤t}=P{X(t)>Xcu}

由此可得任意时刻t产品的可靠度函数R(t)为

R(t)=1-F(t)=P{X(t)≤Xcu}

对于参数漂移系数和扩散系数均为常数时,其可靠度函数为

(2)

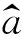
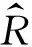
3高可靠产品可靠性寿命分布研究

利用产品性能指标的可靠度函数对产品可靠度进行预测时,当预测时间与检测时刻比较近时估计效果比较好,当预测时间与检测时刻相差比较远时产品可靠度预测会产生较大误差。如果能合理确定产品可靠度的寿命分布,将检测时刻的可靠度数值与寿命分布相结合,可以提高可靠度评估精度。本节介绍常见的寿命分布函数及其参数估计方法。

3.1指数分布

指数分布通常用来描述电子类产品的可靠度,其具有无记忆性。对于服从参数为λ>0的指数分布,其概率密度函数为

f(x;λ)=λe-λx,x>0

设产品可靠度服从指数分布,则各个时刻的可靠度值为

R(ti)=e-λti,i=1,2,…,n

指数分布参数的最小二乘估计为

(3)

3.2正态分布

由于正态分布密度函数的原函数不能用初等函数来表示,所以使用近似计算或搜索的方法对参数进行估计。

1) 参数估计的近似计算法

设随机变量X服从参数为μ,σ的正态分布,其k阶原点矩uk为

利用定积分的定义,通过取被积函数的左端点的值,近似计算出u1,u2,

因此,正态分布的期望和方差的估计值:

(4)

这种参数估计方法具有一定的误差,特别是对于高可靠产品很难得到寿命期内产品的各种可靠度估计值,随着试验样本工作时间的减少参数估计偏差变大。

2) 参数估计的搜索方法

根据先验信息确定参数的大致取值范围,使用搜索的方式确定参数的估计值,即确定参数μ,σ,使得式(5)成立,其中

(5)

这种参数估计方法,在不能大致确定参数取值范围时,搜索范围较大,需要的时间较长。

3.3对数正态分布

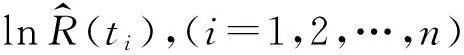
3.4三参数威布尔分布

三参数威布尔分布的概率密度函数为

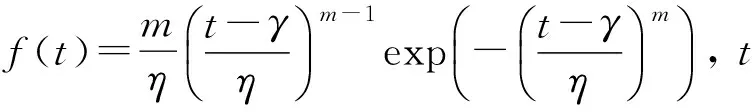
式中γ为保证参数;m、η分别为形状参数和尺度参数。三参数威布尔分布的参数估计见文献[1]。

3.5Gamma分布

若非负随机变量X的概率密度函数[9]为

(6)

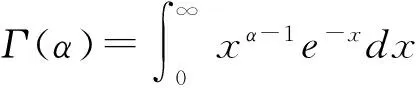
设X～Γ(α,λ),则随机变量的期望和方差分别为

则参数的估计值为

(7)

通过近似计算得到的Gamma分布的参数估计如式(7)所示,该估计方法具有一定的误差,也可以使用搜索的方式确定参数的估计值,即确定参数α,λ,满足下式

(8)

4仿真分析

选取仿真例子,计算在不同时刻的可靠度真值,对于第2节中的常见寿命分布,对参数进行估计,得到寿命分布函数表达式,进而得到可靠度估计值,根据可靠度误差的大小判断寿命分布函数对具有参数漂漂移特征的产品可靠度的适用性。

4.1仿真例子

以文献[10]中液力耦合器的性能指标振动幅值为研究对象,随着时间的增长,液力耦合器的振动幅值会不断增大,当振动幅值超过额定阈值时液力耦合器系统发生退化失效,振动幅值的额定阈值为Xcu=40。对于第三个周期的观测数据,从第三个数据点开始认为振动幅值服从参数漂移模型,使用极大似然估计法计算得到参数估计值为a=0.0091,b2=0.0017,以该参数估计值为仿真例子对产品可靠度寿命分布进行仿真分析。

4.2误差计算

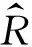
(9)

4.3可获得寿命期内可靠度值时可靠度寿命分布分析

设采样时间为[1,1500]天,此时样本点的可靠度的取值范围为[0.371,1],分别使用指数分布、正态分布、对数正态分布、三参数威布尔分布、Gamma分布对可靠度进行拟合,使用式(3)～式(8)中的参数估计方法对参数进行估计,进而作出可靠度曲线,其中正态分布、对数正态分布、Gamma分布均使用两种参数估计方法对参数进行估计,其中标号为1的是使用搜索的方法对参数进行估计,标号为2的是使用近似积分的方法对参数进行估计。可靠度曲线如图1所示,误差结果见表1所示。图1中的可靠度仿真结果指对于仿真例子使用式(2)计算得到的可靠度值。

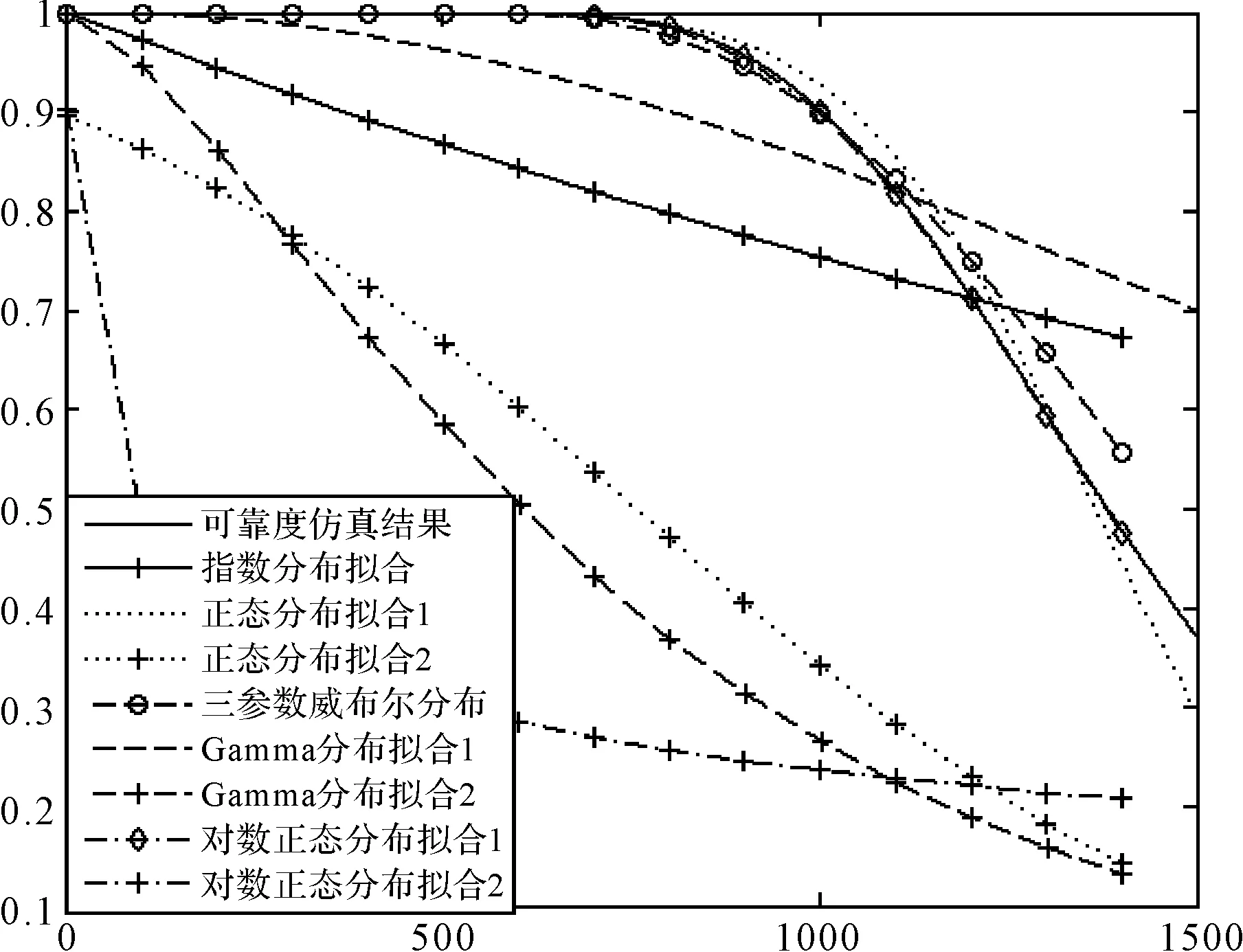
图1　可靠度范围为[0.371,1]时可靠度寿命分布拟合

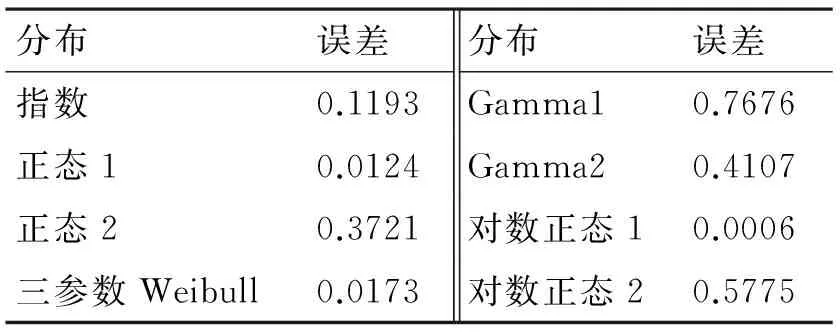
分布误差分布误差指数0.1193Gamma10.7676正态10.0124Gamma20.4107正态20.3721对数正态10.0006三参数Weibull0.0173对数正态20.5775

由图1和表1可知:指数分布、Gamma分布拟合出的可靠度曲线,与仿真例子的可靠度曲线相差较远;正态分布和对数正态分布使用搜索方法得到参数估计值对应的可靠度曲线比近似计算得到的可靠度曲线更接近仿真例子的可靠度曲线。因此,在后续仿真分析中,不考虑指数分布和Gamma分布对高可靠寿命分布的拟合,在使用正态分布和对数正态分布对可靠度曲线进行拟合时,不考虑参数的近似估计方法。

4.4可获得较长时间可靠度值时可靠度寿命分布分析

设采样时间为[1,1200],此时样本点的可靠度的取值范围为[0.7131,1],分别使用正态分布、对数正态分布、三参数威布尔分布对可靠度曲线进行拟合,使用相应的参数估计方法对参数进行估计,进而做出可靠度曲线,其中正态分布、对数正态分布使用搜索方法对参数进行估计。可靠度曲线如图2所示,误差结果见表2所示。

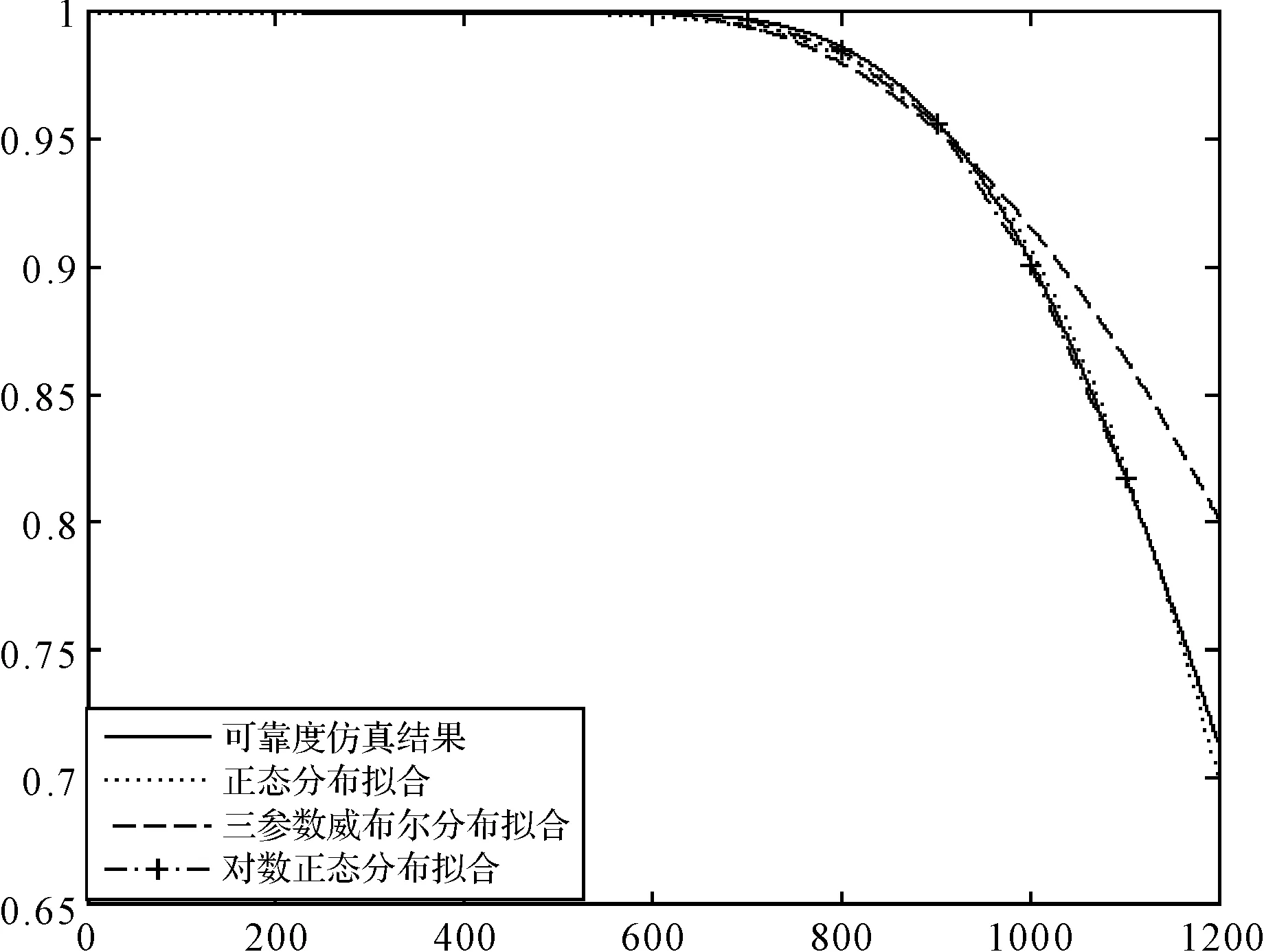
图2　可靠度范围为[0.7131,1]可靠度寿命分布拟合

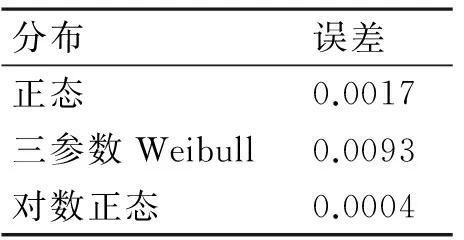
分布误差正态0.0017三参数Weibull0.0093对数正态0.0004

由图2和表2可知,当样本点的可靠度数值在0.8以上时,正态分布、三参数Weibull分布、对数正态分布对于高可靠性产品可靠度值的拟合效果相当,从误差结果来看,三参数Weibull分布的可靠度预测相对来说差距大一些。

4.5可获得高可靠度值时可靠度寿命分布分析

设采样时间为[1,900],此时样本点的可靠度的取值范围为[0.9578,1],分别使用正态分布、对数正态分布、三参数威布尔分布对可靠度进行拟合,使用相应的参数估计方法对参数进行估计,进而做出可靠度曲线,其中正态分布、对数正态分布使用搜索方法对参数进行估计。可靠度曲线如图3所示,误差结果见表3所示。

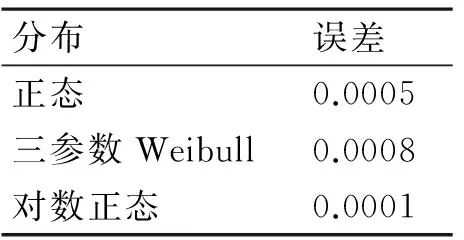
表3　可靠度范围为[0.9578,1]可靠度寿命分布拟合误差

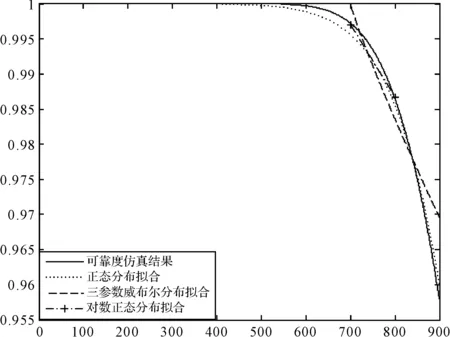
图3　可靠度范围为[0.9578,1]可靠度寿命分布拟合

由图3和表3可知,对于高可靠产品,当样本点的可靠度数值较高且高于0.98时,正态分布、三参数Weibull分布、对数正态分布对于高可靠性产品可靠度值的拟合效果相当,正态分布和对数正态分布比三参数Weibull分布的可靠度预测更精确。

综上所述,对于高可靠产品,其可靠度曲线具有突然下降的特点,使用寿命分布对可靠度曲线进行拟合时,正态分布、对数正态分布、三参数Weibull分布的拟合效果比较好,正态分布、对数正态分布的效果优于三参数Weibull分布,但是这两个分布的参数估计使用搜索的方法,参数范围的选择比较重要,且耗时比较长,三参数Weibull分布使用最小二乘法对参数进行估计,参数估计可以使用表达式进行表示和计算,计算时间比较短。

5结语

本文对具有参数漂移特征的产品可靠性分布规律进行了研究,分析了常见分布,如指数分布、正态分布、对数正态分布、三参数威布尔分布、伽马分布的特点,以及在已知可靠度值时常见分布中的参数估计方法,最后使用仿真分析进行说明,从获得的可靠度值的取值范围的大小从三个方面进行可靠度曲线拟合分析,仿真结果说明,当可以通过先验信息大概确定正态分布或对数正态分布参数的取值范围,并且对计算时间没有要求时,使用正态分布或对数正态分布拟合可靠度曲线效果较好,否则使用三参数威布尔分布效果较优。

参 考 文 献

[1] Chinnam R B. On line Reliability Estimation of Individual Components Using Statistical Degradation Signal Models[J]. Quality & Reliability Engineering International,2002,54(1):3-10.

[2] Si X S, Chen M Y, Wang W B, et al. Specifying Measurement Errors for Required Lifetime Estimation Performance[J]. European Journal of Operational Research,2013,231(3):631-644.

[3] Le Son K, Mitra F, Barros A, et al. Remaining Useful Life Estimation Based on Stochastic Deterioration Models: a Comparative Study[J]. Reliability Engineering & System Safety,2013,112:165-175.

[4] 翟亚利,张志强,钟强晖.具有参数漂移特征的退化可靠性评估方法[J].海军工程大学学报,2013,25(2):107-112.

ZHAI Yali, ZHANG Zhiqiang, ZHONG Qianghui. Degradation reliability evaluation method of products with parameters digression feature[J]. Journal of Naval University of Engineering,2013,25(2):107-112.

[5] 钟强晖,张志华,吴和声.基于退化数据的可靠性评估方法探讨[J].系统工程与电子技术,2009,31(9):2280-2284.

ZHONG Qianghui, ZHANG Zhihua, WU Hesheng. Research on methods about reliability assessment based on degradation data[J]. Systems Engineering and Electronics,2009,31(9):2280-2284.

[6] 钟强晖,张志华,梁胜杰.基于多元退化数据的可靠性分析方法[J].系统工程理论与实践,2011,31(3):544-551.ZHONG Qianghui, ZHANG Zhihua, LIANG Shengjie. Reliability analysis approach based on multivariate degradation data[J]. Systems Engineering-Theory & Practice,2011,31(3):544-551.

[7] 翟亚利,张志华,李大伟.具有漂移特征的退化可靠性评估方法研究[J].系统工程理论与实践,2014,34(10):2710-2715.

ZHAI Yali, ZHANG Zhiqiang, LI Dawei. The method about reliability evaluation based on degradation data with parameters digression feature[J]. Systems Engineering-Theory & Practice,2014,34(10):2710-2715.

[8] 翟亚利,张志华,李大伟.基于冲击理论的性能可靠性评估研究[J].系统工程与电子技术,2014,36(10):2108-2112.ZHAI Yali, ZHANG Zhiqiang, LI Dawei. Performance reliability evaluation based on impact theory[J]. Systems Engineering and Electronics,2014,36(10):2108-2112.

[9] 茆诗松,王静龙,濮晓龙.高等数理统计[M].北京:高等教育出版社,2006:7-9.

MAO Shisong, WANG Jinglong, PU Xiaolong. Advanced mathematical sratistics[M]. Higher Education Press,2006:7-9.

[10] 谭林,程志君,郭波.基于风险的劣化系统最优检测策略[J].系统工程理论与实践,2009,29(9):108-114.

TAN Lin, CHENG Zhijun, GUO Bo. Optimal inspection policy for deteriorating system based on risk[J]. Systems Engineering-Theory & Practice,2009,29(9):108-114.

收稿日期:2016年1月6日,修回日期:2016年2月15日

作者简介:翟亚利,女,博士研究生,讲师,研究方向:装备保障理论。张志华,男,教授,博士生导师,研究方向:装备保障。宋祁,男,硕士研究生,研究方向:备件配置。

中图分类号O141.4

DOI:10.3969/j.issn.1672-9722.2016.07.005

Reliability Distribution of Products with Parameters Digression Feature

ZHAI YaliZHANG ZhihuSONG Qi

(Naval University of Engineering, Wuhan430033)

AbstractFor the products with parameters digression feature, the reliability distribution is studied. The character and parameter estimation methods of the common distributions are analyzed, such as index distribution, normal distribution, logarithmic normal distribution, three-parameter Weibull distribution, and Gamma distribution. For the scope of the product reliability which obtained from the practice is different, the fitting analysis of reliability curve is studied for three kinds of situation. The simulation results demonstrate if the scope of parameters can be obtained before parameter estimation the normal distribution and logarithmic normal distribution are fitting better, otherwise the three-parameter Weibull distribution is fitting better.

Key Wordsparameters digression, reliability distribution, parameter estimation