基于条件滤波的数字视频稳像算法*

潘　磊

(中国民用航空飞行学院计算机学院　广汉　618307)



基于条件滤波的数字视频稳像算法*

潘磊

(中国民用航空飞行学院计算机学院广汉618307)

摘要针对数字视频稳像算法的运动平滑步骤中,采用单一滤波方法适应性较差以及多滤波器方法稳定性不足的问题,提出了一种根据不同类型的噪声选取相应滤波器的条件滤波方法。首先,根据摄像机全局运动的特点,将抖动噪声分为脉冲噪声和随机噪声两类;然后,通过分析参考点的坐标在窗口内各帧中的变化趋势,分别给出上述两类噪声的判别条件;最后,对于脉冲噪声,采用改进的加权均值滤波方法进行运动平滑,而对于随机抖动噪声,则选用高斯滤波方法。同时,还解决了多滤波器方法中的图像跳变问题。实验表明,该方法更为有效地滤除了抖动噪声,并更好地保留了有意运动。

关键词数字视频稳像; 运动平滑; 条件滤波; 加权均值滤波; 高斯滤波

Class NumberTP301.6

1引言

数字视频稳像[1～2]是指利用计算机视觉和数字图像处理的方法,对视频中因拍摄平台不稳定而造成的图像抖动进行滤除,并尽可能保留其中摄像机有意运动,以改善视频视觉效果的技术,常用于手持设备所拍摄视频的后期处理。

一般情况下,数字视频稳像算法主要包含三个步骤[1]:运动估计(Motion Estimation)、运动平滑(Motion Smoothing)和运动补偿(Motion Compensation)。首先,建立一定的运动模型,进行运动估计,得到视频帧之间的全局运动矢量;然后,对运动估计得到的全局运动矢量进行运动平滑,以滤除抖动噪声,并保留摄像机的有意运动;最后,根据运动平滑的结果进行运动补偿,从而得到稳定的视频帧序列。其中,运动平滑是达到稳像目的的关键步骤,其性能直接影响到最终的稳像效果。

运动平滑主要通过滤波来实现,主要分为两大类:一类是通过单一滤波器实现,另一类是采用多个滤波器实现。目前,常用的单一滤波器方法主要有高斯滤波[1]、卡尔曼滤波[3]和粒子滤波[4]等。其中,卡尔曼滤波和粒子滤波基于固定参照帧的运动模型,容易带来累计误差;高斯滤波解决了累计误差的问题,且能较好地保留有意运动,但对抖动噪声的滤除能力不足。文献[5]对文献[1]中的高斯滤波进行了改进,在一定程度上提高了其平滑能力,但仍无法适用于抖动剧烈的情况。上述滤波方法各具优缺点,适用于不同的情况,因此,采用单一滤波器的运动平滑方法难以在整体上获得最佳效果,适用性较差。文献[6]提出了一种结合两类低通滤波器的混合滤波方法,该方法根据视频帧抖动幅度的不同,选取相应的低通滤波器,与单一滤波器相比,具有更好的效果。然而,滤波器的性能主要与噪声类型有关,根据视频帧的抖动幅度来选择滤波器具有一定的局限性,且相关阈值需要根据经验和视频的实际情况进行手动设定,缺乏通用性;另外,由于未进行相应的处理,在两种滤波器的切换时会存在图像的跳变现象,严重影响了稳像的效果。

为解决运动平滑中单一滤波器方法适用性低,以及现有多滤波器方法性能不足的问题,本文提出了一种基于条件滤波的数字稳像算法,借鉴文献[6]中结合多种滤波器进行运动平滑的思想,根据不同类型的噪声来选取相应的滤波器。其基本思路是:将视频中的抖动噪声分为脉冲噪声和随机抖动噪声两类,并给出它们的判别条件;对于脉冲噪声,提出一种改进的加权均值滤波进行处理,而对于随机抖动噪声,则采用高斯滤波,尽可能在滤除抖动噪声的同时,保留有意运动;此外,在滤除脉冲噪声后,采用滤波后的值代替原始值进行后续的滤波操作,从而避免了滤波器切换时的图像跳变问题,且避免了二次滤波,减少了计算代价。

本文的贡献主要表现在以下几个方面:第一,首次对抖动噪声进行了分类,并给出了相应的判别条件,以便更有针对性地进行运动平滑;第二,解决了运动平滑中现有多滤波器方法存在的图像跳变现象,提高了稳定性;第三,根据视频稳像自身的特点,针对脉冲抖动噪声,提出了一种改进的加权均值滤波器,从而达到更好的运动平滑效果。

2运动估计

运动估计的目的是获取摄像机的原始运动轨迹,可以通过2D模型[1]或3D模型[7]来实现。用于描述摄像机运动的参考系,则主要有固定参考帧[3～4]、可变参考帧[8]和无参考帧[1]三种。

综合考虑精确性、稳定性和运算复杂度等方面的因素,本文采用文献[7]中提出的运动估计方法,基于无参考帧的2D仿射模型,利用ORB特征点[9]进行图像匹配,来计算帧间像素点的坐标变换矩阵。从第m帧到第n帧像素点的坐标变换可表示为

(1)

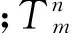
3基于条件滤波的运动平滑

运动平滑是稳像的关键步骤,通常利用低通滤波器来实现。然而,在一般情况下,不同的低通滤波器具有各自的优势,适用于不同类型噪声的滤除。因此,本文提出了一种基于条件滤波的运动平滑方法,先对抖动噪声进行分类,再针对不同类型噪声,采用相应的滤波器。该方法是本文的核心内容,详细流程见3.4节。

3.1抖动噪声分类

从摄像机的运动轨迹来看,因拍摄平台不稳定而造成的视频抖动噪声大致可以分为以下两种情况:其一,抖动噪声相对较均匀地分布在摄像机有意运动轨迹的两侧,未在局部形成较明显的偏离;其二,某个位置包含的抖动噪声在摄像机有意运动轨迹的一侧产生跃变,在局部形成了明显的偏离。需要指出,上面所说的摄像机有意运动轨迹是指理想状态下只包含有意运动,而不包含抖动噪声的摄像机运动轨迹,其中的“有意运动”和“抖动噪声”都按一般意义上的理解来进行判断。

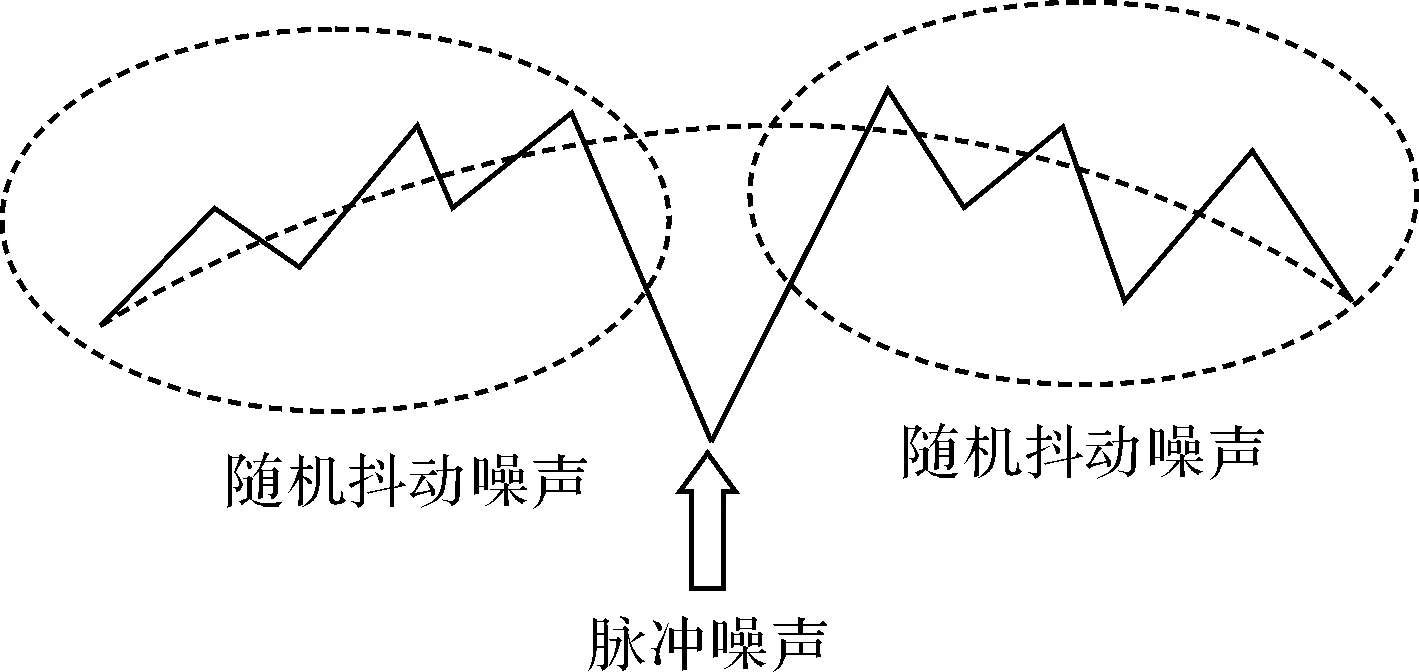
图1　随机抖动噪声与脉冲抖动噪声

抖动噪声表现出的这种特征与文献[10]中所描述的图像噪声的情况类似,将上面描述的第一种抖动噪声称为随机噪声,第二种则称为脉冲噪声。如图1所示,其中,虚线表示摄像机有意运动轨迹,实线表示摄像机的实际运动轨迹;虚线框内的点只包含随机噪声,箭头所指的点则包含了脉冲噪声。由于本文的运动估计基于2D仿射模型,摄像机的运动轨迹也采用2D模型来描述,只考虑摄像机投影到像平面上的运动。

3.2抖动噪声的判别

从上述随机噪声和脉冲噪声的描述可以看出,二者的差异主要体现在摄像机运动轨迹的局部特征上。文献[10～11]根据极值来判别图像中的脉冲噪声,本文借鉴这种思路,结合抖动噪声的特点,根据摄像机位置坐标的局部偏离程度来判别脉冲噪声。

将摄像机看成质点,像平面中心点的坐标则代表了该时刻下摄像机的位置坐标。以视频首帧的图像坐标系作为参考系,首帧图像中心点的像素坐标C0=(x0,y0)则为摄像机的起始位置坐标,根据帧间像素点的坐标变换矩阵,可以得出后续各帧的摄像机位置坐标。第t帧摄像机的位置坐标(以下简称位置坐标)为

(2)

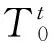
在摄像机的运动轨迹中,以当前帧序号t为中心,取半径为r(r为大于1的整数)的邻域,则帧序号落在该邻域内且与第t帧相邻的所有点的位置坐标构成的集合为

Nt={(x,y)|(x,y)∈Ci,i∈[t-r,t+r]}

(3)

第i帧位置坐标的局部偏离程度可以通过分析Nt中各坐标点到它们中心位置的欧氏距离来考察。Nt中所有点的中心位置坐标为

(4)

当第t帧位置坐标离中心位置的欧氏距离D(Ct,Mt)大于某一阈值DThreshold时,则认为该点在局部的偏离较大,判别为脉冲噪声点,用gt=1来标记;否则,判别为随机噪声点,置gt=0,即:

(5)

式(5)中的DThreshold可根据Nt中各点到中心位置的欧氏距离的均值μD和标准差σD进行动态设定,如式(6):

DThreshold=μD+λσD

(6)

其中,λ为松弛变量,影响脉冲噪声判别的敏感程度,参数设置情况详见3.3.3节。

3.3条件滤波

为了更有效地滤除抖动噪声,并尽可能地保留摄像机的有意运动,本文提出了一种条件滤波的方法,在脉冲噪声和随机噪声这两种不同的抖动噪声条件下,分别采用改进的加权均值滤波器和高斯滤波器进行滤除,以达到理想效果。

3.3.1改进的加权均值滤波

图像中的脉冲噪声可采用中值滤波[12]或其相关改进方法[10～11,13]来滤除。本文根据运动平滑和抖动噪声自身的特点,提出了一种改进的加权均值滤波方法来滤除抖动噪声中的脉冲噪声。在脉冲噪声的影响下,该时刻摄像机的位置坐标相对于摄像机有意运动轨迹来说产生了较大的偏离,需要对其进行重新定位,以还原摄像机的有意运动。

假定第t帧判别为脉冲噪声点,以第t帧为中心取半径为k的滤波窗口,窗口内的所有帧构成的集合记为Ut。去除第t帧,则Ut中的剩余帧所构成的集合为

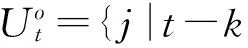
(7)

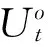
(8)

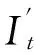
(9)

式(8)中的权重Wi由第i帧与第t帧之间相隔帧数的倒数经过归一化来确定,如式(10):

(10)

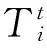
3.3.2高斯滤波

对于抖动噪声中的随机噪声,本文采用文献[1]中提出的高斯滤波来进行滤除,补偿矩阵计算方法如式(11):

(11)

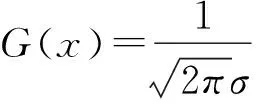
高斯滤波能够很好地保留摄像机有意运动,对于随机噪声这中在局部范围内分布相对较均匀且未产生较大偏离的抖动噪声的滤除,能够取得良好的效果。

3.3.3参数设置

本文需要设置的参数主要有:抖动噪声判别中所用到的邻域半径r、松弛变量λ以及滤波窗口半径k。其中,邻域半径r和滤波窗口半径k都用于控制“局部”的尺度,r影响脉冲噪声判别的敏感程度,k则决定了滤波结果的平滑程度。一般情况下,r值越大,脉冲噪声判别的敏感程度越低;而k值越大,滤波结果的平滑程度越高。在方法的实现时,r和k通常可以取相同的值。松弛变量λ是影响脉冲噪声判别敏感程度的另一个参数,λ值越大,敏感程度就越低,其取值应该参考k的大小。

结合文献[1]中给出的k取值的相关建议,经过大量实验发现,当r和k都取6,λ取[0.5,2]时,对大多数视频能获得较理想的效果。本文实验统一将以上参数分别设置为r=k=6和λ=0.5。

3.4方法详细流程

综上所述,本文提出的基于条件滤波的运动平滑方法详细流程如图2所示。

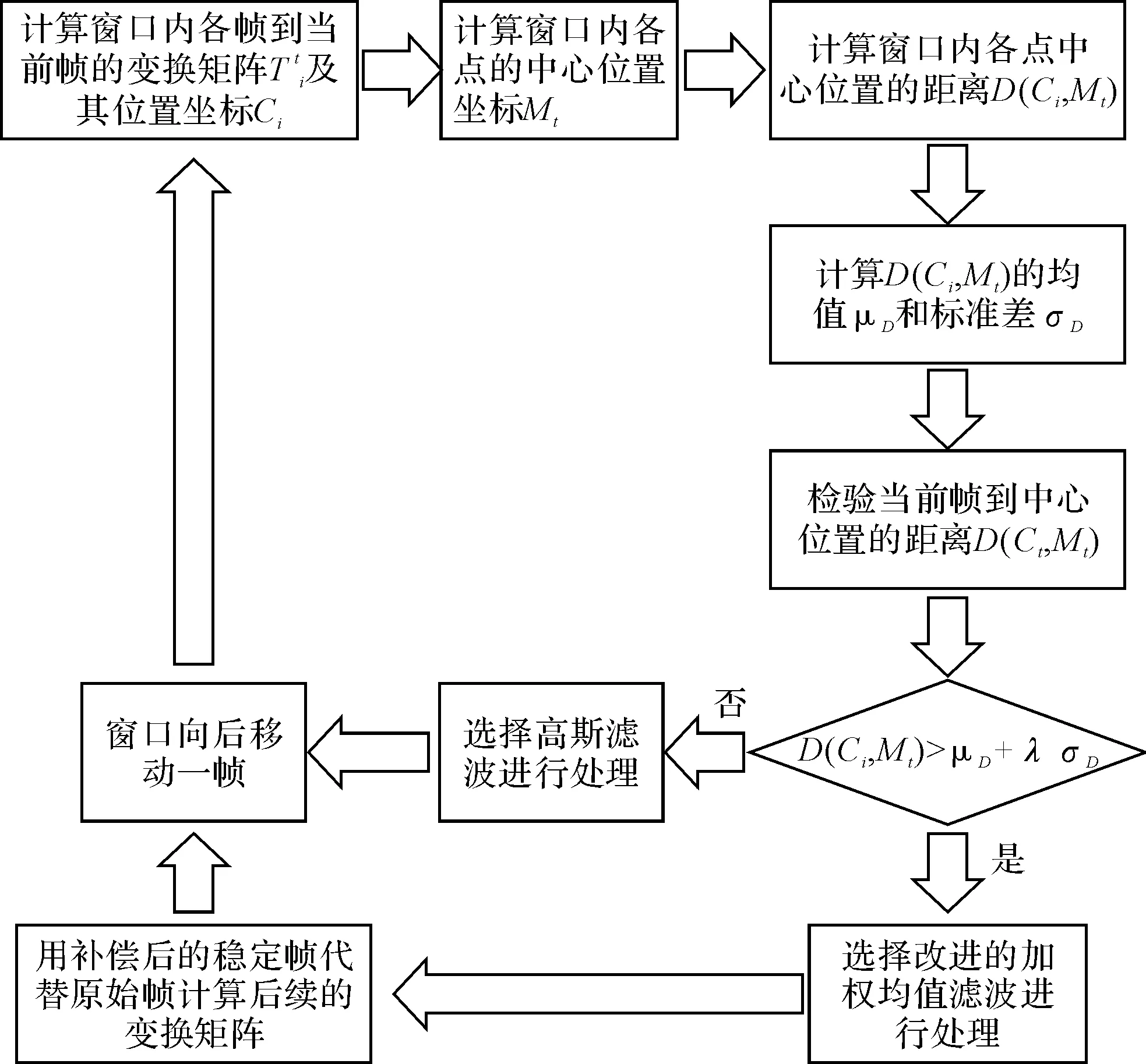
图2　本文方法详细流程图

需要指出,如文献[10]中所述,消除两种噪声通常要进行两次滤波处理。而本文在使用改进加权均值滤波消除了脉冲噪声后,采用稳定帧代替原始帧计算后续的变换矩阵,能够取得与两次滤波处理基本一致的结果,同时还避免了因滤波器切换而造成的图像跳变现象。

4实验分析

为了验证算法的有效性,本文选取了文献[7]中的三段测试视频和一段自摄视频来进行实验,将它们统一编号为V1、V2、V3和V4。以上所有视频均由普通相机或手机拍摄,其中,V1和V2的分辨率为640*360,V3和V4分别为1280*720和856*480,如图3所示。

图3　测试视频

实验程序用C++编写,开发平台为opencv 2.4.10+Visual Studio 2010,硬件环境为Intel i3 2.13GHz+4G内存,分别与高斯滤波[1]、改进高斯滤波[5]以及混合低通滤波[6]这三种方法进行对比,观察各方法处理前后的摄像机运动轨迹,并比较处理结果的帧间相似程度。

需要指出,关于混合低通滤波方法中参数Var(D)的设定,文献[6]中给出的参考取值为7,但由于本文测试视频的分辨率都远大于文献[6]中的320*240,Var(D)的值必须做一定的调整,才能获得好的效果。因此,本文的实验中将Var(D)的值设置为25、25、40和30,分别对应V1,V2,V3和V4。

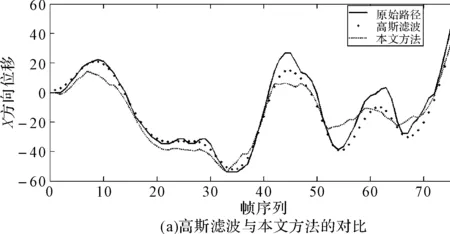
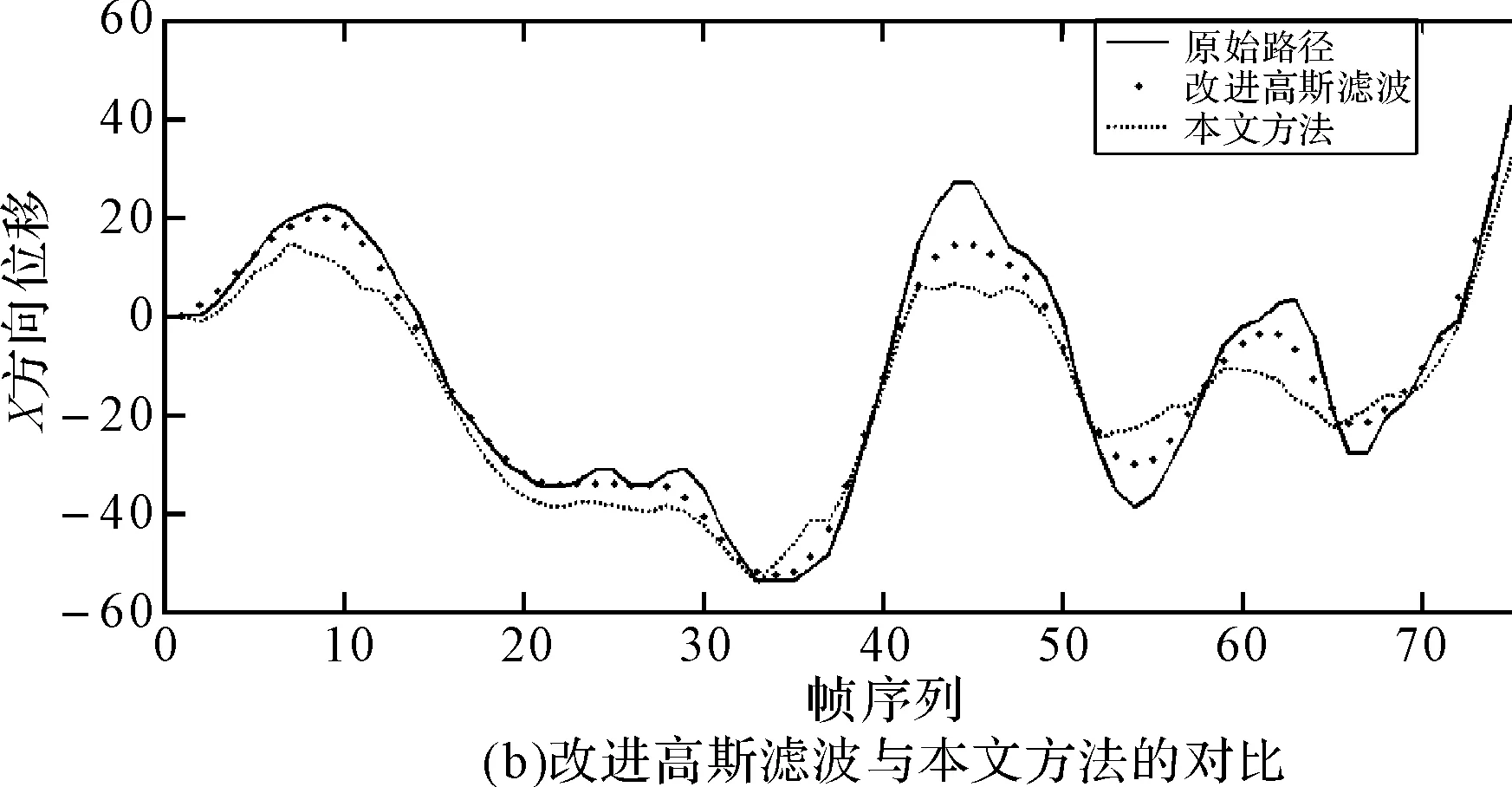
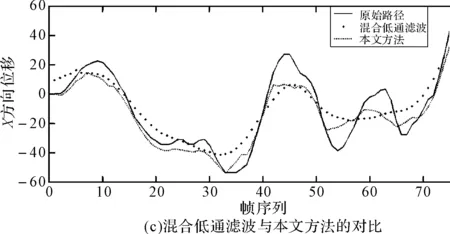
图4　基于视频V1,各方法与本文算法的位移对比图

以V1和V4中摄像机X方向的位移为例,各方法处理前后的摄像机路径如图4、图5所示。从图中可以看出,高斯滤波和改进高斯滤波的处理结果差别不大,摄像机有意运动保留得较为完整,但对抖动噪声的滤除不够;混合低通滤波得到了较为平滑的路径,但处理后的路径偏离原始路径较多,误差较大,并且在实验过程中发现该方法在两种滤波器进行切换时会发生明显的跳变现象;本文的方法则在保留了摄像机有意运动的同时,有效地滤除了大部分的抖动噪声,特别是脉冲噪声,如V1视频中的40～70帧,V4视频中的30～40帧、60～70帧。与前三种方法相比,效果更加理想。

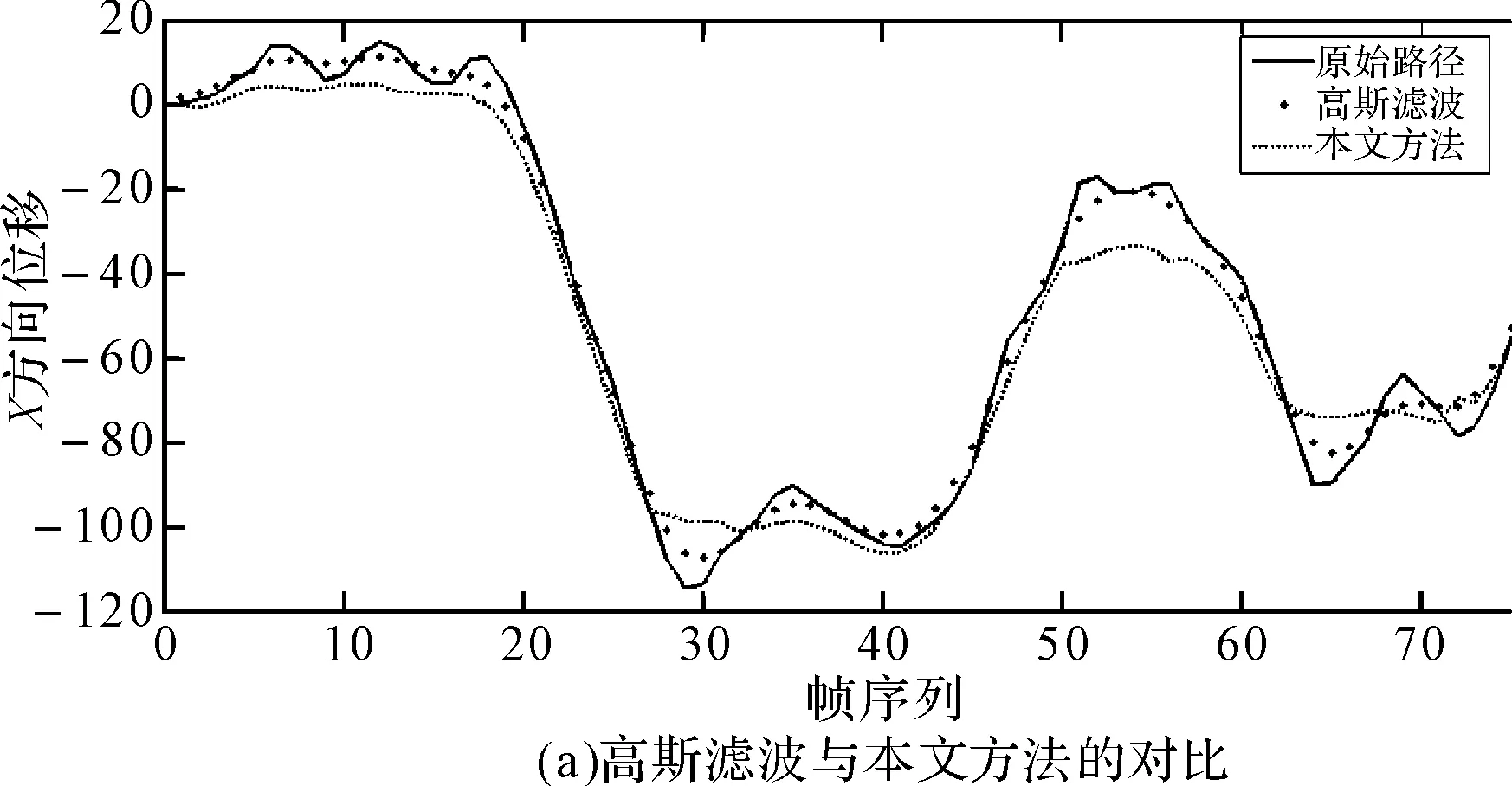
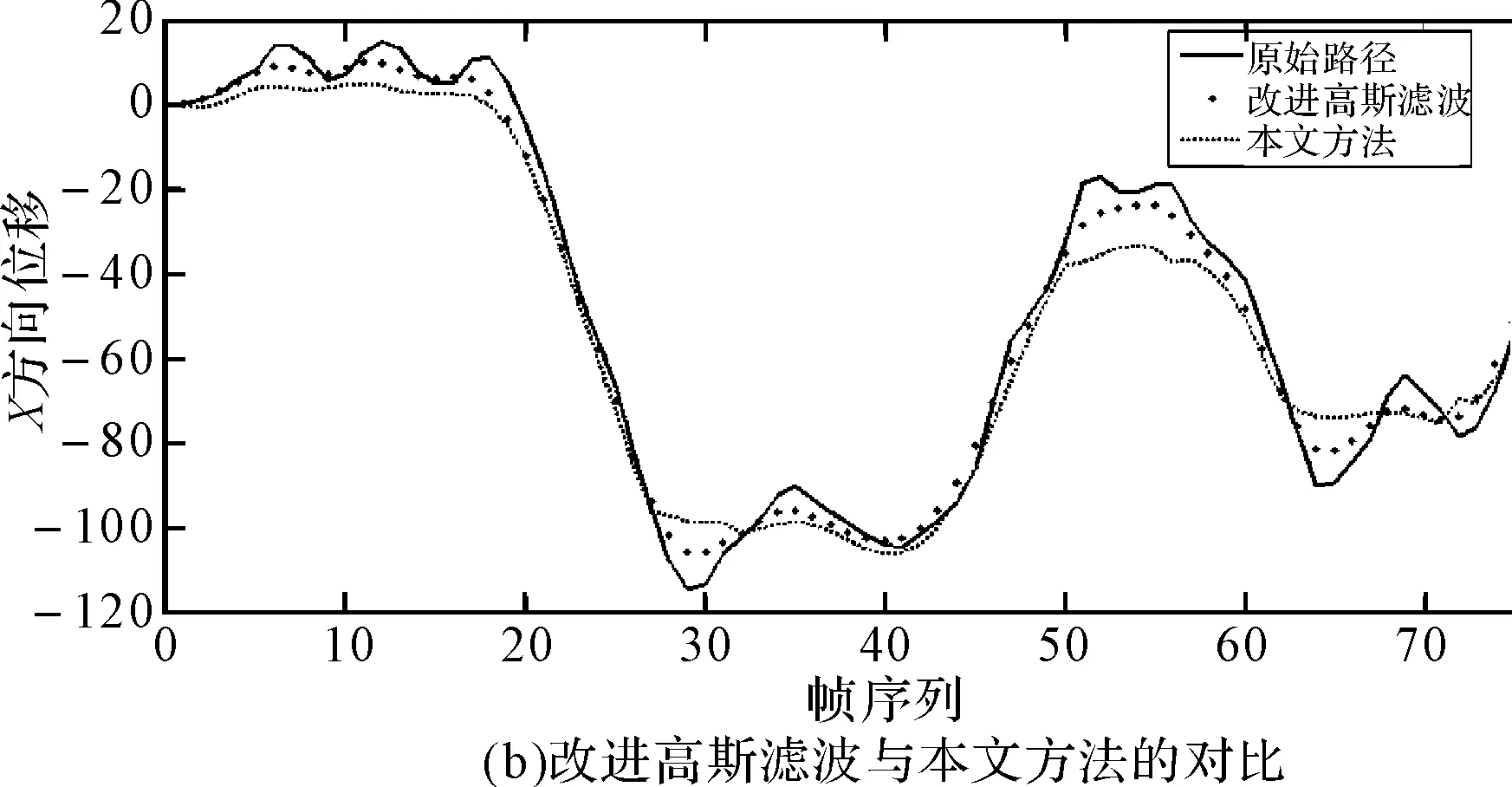
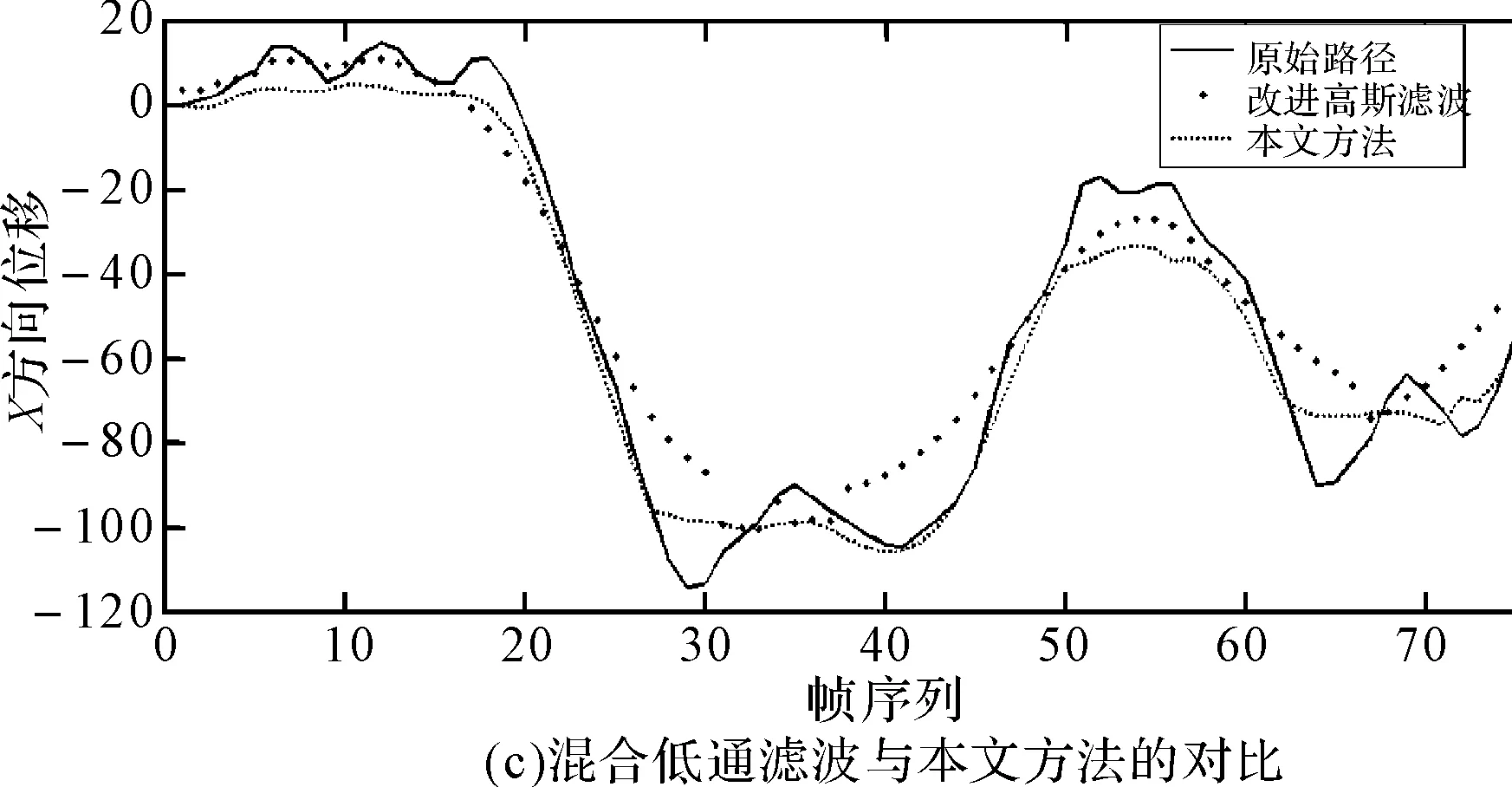
图5　基于视频V4,各方法与本文算法的位移对比图

帧间变换保真度(Inter-frame Transformation Fidelity,ITF)[14]可以用来测量视频中相邻帧之间的相似程度,能在一定程度上检验稳像的效果。ITF越大,帧间相似度越高,则说明视频越稳定。ITF计算公式如下

(12)其中,PSNR(k)为第k帧与k+1帧的峰值信噪比。

表1列出了各方法对所有测试视频处理结果的ITF值。从测试视频的处理结果来看,本文方法的ITF值基本上优于其他方法,只在对视频V1的处理结果上略低于混合低通滤波。然而,混合低通滤波的ITF值不太稳定,对V1和V3的处理结果表现得较高,对V2和V4则较低,这是滤波器切换时的跳变现象造成的。由于本文方法在滤除脉冲噪声之后采用了稳定帧代替原始帧来计算后续的变换矩阵,因此不存在上述跳变现象,运行结果更为稳定。

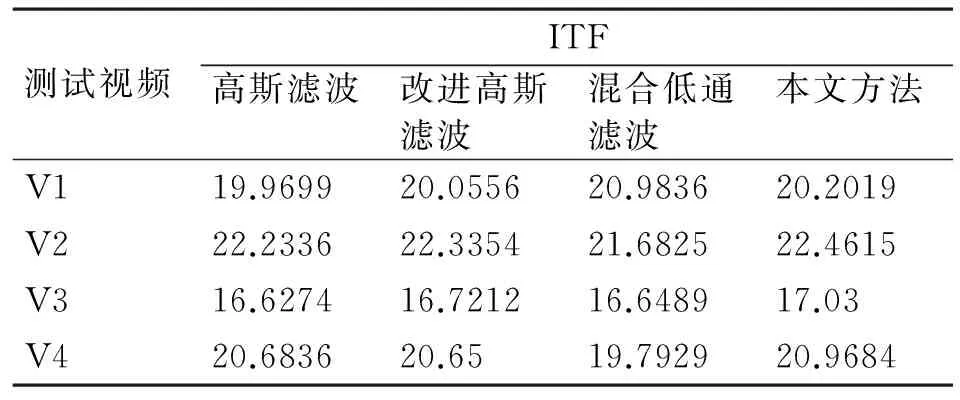
表1　各方法的ITF对比

5结语

本文提出了一种基于条件滤波的运动平滑方法,利用不同滤波器各自的优势,根据不同类型的抖动噪声,选取相应合适的滤波器,从而有效地进行运动平滑,在滤除抖动噪声的同时,尽可能地保留摄像机的有意运动。同时,在多滤波器运动平滑方法中,解决了因滤波器切换造成的图像跳变问题。通过实验表明,相对于现有方法而言,该方法具有更好的效果和稳定性。

考虑到该方法中的噪声分类方法主要考虑摄像机平移运动,而对于摄像机的旋转和缩放运动,具有一定的局限性,有待于进一步的研究。

参 考 文 献

[1] Matsushita Y, Ofek E, Ge W, et al. Full-frame video stabilization with motion inpainting[J]. IEEE Transaction on Pattern Analysis and Machine Intelligence,2006,28(7):1150-1163.

[2] 王志民,徐晓刚.电子稳像技术综述[J].中国图象图形学报,2010,15(3):470-480.

WANG Zhiming, XU Xiaogang. A Survey on Electronic Image Stabilization[J]. Journal of Image and Graphics,2010,15(3):470-480.

[3] Litvin A, Konrad J, Karl W. Probabilistic video stabilization using Kalman filtering and mosaicking[C]//Image and Video Communication and Processing 2003. Bellingham: Spie-Int Soc Optical Engineering,2003:663-674.

[4] Yang J, Schonfeld D, Mohamed M. Robust video stabilization based on particle filter tracking of projected camera motion[J]. IEEE Transaction on Circuits and Systems for Video Technology,2009,19(7):945-945.

[5] Xu J, Chang H W, Yang S, et al. Fast feature-based video stabilization without accumulative global motion estimation[J]. IEEE Transactions on Consumer Electronics,2012,58(3):993-999.

[6] 许杰,杨硕,王明辉.基于抖动帧检测和低通滤波的数字视频稳像算法[J].四川大学学报(自然科学版),2013,50(6):1235-1240.

XU Jie, YANG Shuo, WANG Minghui. Digital video stabilization based on jittery frame checking and low-pass filtering[J]. Journal of Sichuan University(Natural Science Edition),2013,50(6):1235-1240.

[7] Liu F, Gleicher M L, Jin H, et al. Content-preserving warps for 3D video stabilization[J]. ACM Transactions on Graphics,2009,28(3):341-352.

[8] Gleicher M L, Liu F. Re-cinematography: improving the camerawork of casual video[J]. ACM Transactions on Multimedia Computing Communications and Applications,2008,5(1):427-438.

[9] Rublee E, Rabaud V, Konolige K, et al. ORB: an efficient alternative to SIFT or SURF[C]//ICCV2011: 2011 IEEE International Conference on Computer Vision. New York: IEEE,2011:2564-2571.

[10] 张旭明,徐滨士,董世运,等.自适应中值-加权均值混合滤波器[J].光学技术,2004,30(6):652-655,659.

ZHANG Xuming, XU Binshi, DONG Shiyun, et al. Adaptive median-weighted mean hybrid filter[J]. Optical Technique,2004,30(6):652-655,659.

[11] 邢臧菊,王守觉,邓浩江,等.一种基于极值中值的新型滤波算法[J].中国图象图形学报,2001,6(6):533-536.

XING Cangju, WANG Shoujue, DENG Haojiang, et al. A New Filtering Algorithm Based on Extremum and Median Value[J]. Journal of Image and Graphics,2001,6(6):533-536.

[12] Gallagher N C, Wise G L. A theoretical-analysis of the properties of median filters[J]. IEEE Transactions on Acoustics Speech and Signal Processing,1981,29(6):1136-1141.

[13] Nodes T A, Gallagher N C. Median filters: some modifications and their properties[J]. IEEE Transactions on Acoustics Speech and Signal Processing,1982,30(5):739-746.

[14] Shen Y, Guturu P, Damarla T, et al. Video stabilization using principal component analysis and scale invariant feature transform in particle filter frame work[J]. IEEE Transactions on Consumer Electronics,2009,55(3):1714-1721.

收稿日期:2016年1月18日,修回日期:2016年2月20日

基金项目:中国民航总局应用开发科技项目(编号:MHRD20140212);中国民用航空飞行学院面上基金项目(编号:J2012-40);四川省教育厅科研项目(编号:16ZB0032)资助。

作者简介:潘磊,男,讲师,研究方向:图像处理、模式识别。

中图分类号TP301.6

DOI:10.3969/j.issn.1672-9722.2016.07.003

Digital Video Stabilization Based on Conditional Filter

PAN Lei

(College of Computer Science and Technology, Civil Aviation Flight University of China, Guanghan618307)

AbstractIn the process of motion smoothing for digital video stabilization, since one kind of filter is poor of adaptability and multi-filter is lack of stability, a conditional filter method which uses the corresponding filter in accordance with different type of jitter noise is proposed in this paper. At first, according to the characteristics of global motion of camera, jitter noise is classified as two types, including impulsive noise and random noise. Then, by analyzing the changing trend of coordinate of reference points in the filter window, sufficient conditions for these two types of noise are given. At last, two different motion smoothing methods, namely, improved weighted mean filter and Gaussian filter are employed for the two types of noise respectively. Meanwhile, image jitter has been solved in multi-filter. Experiments show that, compared with the method of single Gaussian filter, improved Gaussian filter and mixed low-pass filter, the proposed method is more effective to filter jitter noise and preserve the desirable motion.

Key Wordsdigital video stabilization, motion smoothing, conditional filter, weighted mean filter, Gaussian filter