基于GARCH模型的股指期货套利策略研究

汪雅倩，朱家明

基于GARCH模型的股指期货套利策略研究

汪雅倩，朱家明

从股指期货上市后的活跃度看，该市场有很大的发展空间。从量化投资角度研究股指期货的套利策略和风险管理。在对股指期货进行分析后，得到股票指数的计算方法和期货的定价方式。根据指数时间序列建立GARCH模型，来对股指期货进行跨期套利分析，并给出相应的套利策略。从时间序列角度对上证指数作预测，了解上证指数的走势。根据历史数据对行情进行分析，在建立模型后，用时间序列的曲线估计进行收益率预测，通过分析时间序列的变化，建立GARCH模型，评估股指策略的收益情况，并进行跨期套利。

统计套利；协整；股指期货套利；GARCH模型

股指期货SPIF在石油危机后应运成为一种可有效避免风险，实现资产保值的金融工具。股指期货指的是买方和卖方以股价指数为标的物，按照商榷的条件在将来某天进行交割的标准化期货合约，一般通过现金结算差价。其在规避风险的同时也可为以后适时推出外汇期货等金融衍生品提供经验。股指期货一般具有股票特性、期货特性：相比于商品期货，股指期货的买卖双方应深入了解经济走势、行业变动和权重较大的成分股动态；相比于商品期货的实物即时交割，股指期货惯用现金交割，未平仓的结算价格一般为末交易日收盘前一段时间现货价格加权。在我国目前的经济条件下，开展股指期货并通过量化有效地控制其风险，对我国证劵市场的规范和发展具有重要意义。

在统计套利的基础上，结合了GARCH模型，基于模型的套利方式使用于异方差性金融序列上，可以制定出更加灵活、精确和持重的交易策略。

一、相关文献综述

在国外，对统计套利及股指期货的实证分析一直是金融研究的热点。G.Vidyamurthy基于统计套利是基于相对价值开展起来的观点，首次将其和协整策略联合，用协整系数表示配对股票间的价格关系［1］。N.S.Thomaidis结合GARCH模型与BP神经网络分析价差数据动态性，以搜寻可能存在的组合套利机会［2］。L.Cui等人提出使用创新的T-GARCH模型以分析期货间短期价格协整关系及不对称价格方差的传递，得到该模型给予更平稳确切的交易门槛而获得更高收益的结论［3］。

国内学者对股指期货套利的理论框架和套利策略的研究也作出了较多贡献。仇中群等人基于实证结果，分析相较于其余跟踪误差法，运用协整存在更大套利空间，并易于削弱风险［4］。陈之远使用统计套利方法，基于仿真数据研究，实证结果表明国内股市不成熟，股价波动大，短期有较大套利空间［5］。李世伟使用沪深300股指期货数据，利用改进的协整理论进行套利操作，认为改良的协整套利策略能获较佳套利结果［6］。陈姚祥基于实证分析得知GARCH模型跨期套利收益较佳，并表示价差数据方差扩展倍数越大，存在的套利空间越小，同时风险也有所减小［7］。

二、股指的计算及期货的低价

（一）指数的计算

股价均值是某时点上市股价绝对数，经差异时点对比，可分析股价的动态趋向。在股价平均数基本分类中，权重股是按照每期样股相对重要程度进行赋权，权重按数量为买卖股量、股票发布数等；按时间分类成t日权数和T日权数。目前惯用的派许指数是以T日买卖股数（或发布数）为权数。

T+t日时指数计算公式为：

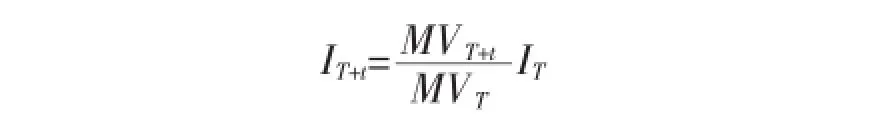
式中：I表示指数；MV表示调整总市值。

（二）股指期货的定价

基于现货-远期平价理论建立理想条件下股指期货远期定价模型：

式中：t为基期；S为基期的标的物价格；f为远期（期货）多头在基期的价值；T为报告期；ST为报告期的标的物价格（基期时未知该值）；r为报告期时按持续复利得出的基期年利率；k为远期（期货）合同的交割价格。

用F表示收益率已知的标的物远期价格，则F的计算公式为：

这就是理想条件下股指期货远期合约定价公式，若不满足式（3）中的关系，就存在套利机会。

如果F＞Se（r-q）（T-t），投资者能通过购进股指的成分股，同时卖出指数期货合约以赚取无风险套利利润；相反，如果F＜Se（r-q）（T-t），投资者能通过卖空股指的成分股，并购进该远期合约以赚取无风险套利。

三、股指期货跨期套利模型的建立

由股指期货套利原理可知，期货市场中，股价受众多因素影响而随时间波动，股价波动不确定性给予了套利策略实施的空间。股指期货跨期套利的交易所、标的类型相同，但交割时间有异。其在不同时间价格有异，若价差远离理想状态，则有无风险跨期套利的可能。统计套利方法是经过分析不同时间交割价差的变化，得到有据的变化区间，在现实价差偏离时，则进行套利。具体做法是：在以往价差水平基础上剖析价差平稳度及指标间长期均衡性，并策划比较合理的套利模式，不必就形式作出预测及估算，而且可以分析出最优套利的可能性。

（一）历史移动法预测长期趋势

假设末期的观测值为xT，可通过收集历史数据，根据历史移动平均法公式来预测当天的收盘价。公式如下：

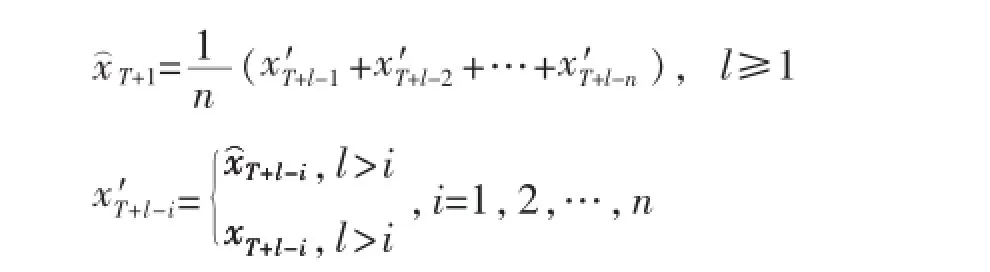
（二）基于GARCH模型的跨期套利

1.协整检验

假设某经济变量与其他经济系统相联系，则长期看来这些变量需存在均衡性，这是模型构造检验的根基。短期内，随机干扰使其远离平均数：若偏离是临时的，则长期仍能恢复平衡；若偏离无法改变，则不认为该些变量有均衡性。理论上，时间序列分析时的序列需稳定，也就是无随机性或确定性，不然可能出现“伪回归”。但金融数据通常非平稳，需在差分后将其平稳化，但此举会丢失总量的长期信息，而该信息对问题的分析是不可或缺的，则可用协整 （co-integration）来解决现有的矛盾。

对于随机向量Xt=（x1t，x2t，…，xnt），若已知Xt～I（d），存在一个N×1阶矩阵β（β≠0），有βTXt～I（d-b），可知指标x1t，x2t，…，xnt有（d，b）阶的协整性，用Xt～I（d，b）表示，β为协整矩阵。

2.GARCH模型的建立

GARCH模型是广义ARCH模型。一般而言，GARCH（0，p）模型，等同ARCH（p）模型。

ARCH（p）可以写为：

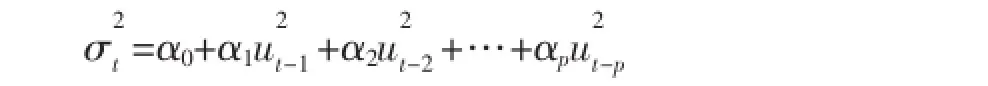
若干扰项标准差不存在自相关，则

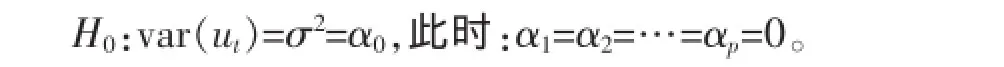
OLS残差：yt=γ0+γ1x1t+…+γkxkt+ut。

标准化CARCH（0，p）模型中：

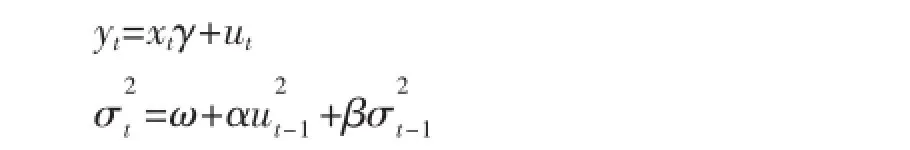
式中：xt为1×（k+1）阶外生变量矩阵；γ为（k+1）×1阶系数矩阵。

（三）实例分析

本次研究选择上证指数（00001）2015年3月27日到2016年3月25日的收盘价，共241个数据作为时间序列，利用Eviews软件对序列建立GARCH模型，并研究收益波动率给出套利方案。

现对数据进行对数处理，上证时间序列均值为0.000 222，标准差为0.024 815，p值为0。然后对序列做ADF检验，得到t统计量为-13.185 85，p值为0，表明序列平稳。

序列自相关及偏自相关系数都进入了2倍标准差预计值里，同时Q统计量的概率P＞5%，故序列在α=0.05时无明显相关关系。

将x去均值化，得到w，并建立CARCH（1，1）模型。CARCH（1，1）系数都通过t检验，建模效果较好，对T-GARCH模型和E-GARCH模型结果分析知E-GARCH效果最好，所以选择EGARCH模型，并对模型进行ARCH-M检验。由检验结果可知系数不显著（用Variance时系数一样不显著），说明不存在ARCH-M过程。

因此，可以得到模型：

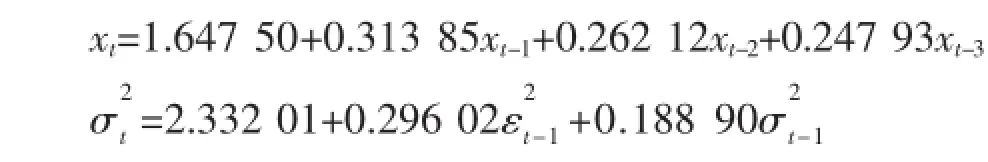
对均值式的残差项εt做LM检验，结果显示，不存在ARCH效应。

通过分析，可以得到所采取的交易策略是：第一，x3＜-1，则做牛市跨期套利；第二，x3＞1，则做熊市跨期套利；第三，建立套利头寸后，当x3回落至区间［-1，1］时，进行反向操作，了解套利头寸；第四，当近期合约到期后，无论价差是否回落，反向对冲了结套利头寸，不进行展期操作。

基于GARCH模型的跨期套利统计结果见表1。

表1　基于GARCH模型的跨期套利结果

四、结论

一般而言，统计套利是种借助不同到期日价差远离长久均衡区间的程度，对冲套利头寸而获利的交易方式。其不同于单纯分析不同到期日期货走向而投机，而是股指期货套利的创新。该模型套利效果较佳，投资者可依据历史价差动态性、风险偏好、期望值收益对模型做调整，以得理想收益。

利用统计套利的跨期套利在实行中有待考究。首先，使用以往数据建模，变动趋势不能真实表示指标间新关系，从而模型需频繁纳入新数据以确保准确性；其次，对于协整抑或CARCH，阈值设定的差异会引致交易活动的差异，进而带来不同利润；最后，风险偏好和投资方式有异的投资者在同种阈值设定下收益也不同。在此强调，跨期套利并非无风险，价差风险、保证金风险不可忽视，市场不稳时，投资者应有足量流动资金维持保证金水平。同时，止盈止损阈值的设置对投资者较为必要。

［1］VIDYAMURTHY G.Pairs Trading：Quantitative Methods and Analysis［J］.New Jersey，2004（13）.

［2］THOMAIDIS N S.Efficient Statistical Analysis of Financial Time-Series Using Neural Networks and GARCH Model［C］. Social Science Electronic Publishing，2006.

［3］CUI L，HUANG K，CAI H J.Application of a TGARCHWavelet Neural Network to Arbitrage Trading in the Metal Futures Market in China［J］.Quantitative Finance，2013（2）.

［4］仇中群，程希俊.基于协整的股指期货跨期套利策略模型［J］.系统工程，2008（12）.

［5］陈之远.行为统计套利模型在中国股票市场中的应用研究［D］.南京：南京财经大学，2011.

［6］李世伟.基于协整理论的沪深300股指期货跨期套利研究［J］.中国计量学院学报，2011（2）.

［7］陈姚祥.股指期货跨期套利研究：基于GARCH模型［J］.中国企业家，2013（12）.

（编辑：唐龙）

F830.93

A

1673-1999（2016）06-0038-03

汪雅倩（1995-），女，安徽财经大学（安徽蚌埠 233030）金融学院2013级在读本科生，研究方向为金融学；朱家明（1973-），男，硕士，安徽财经大学统计与应用数学学院副教授，研究方向为应用数学与数学建模。

2016-03-28

国家自然科学基金项目“随机动力系统的非一致指数二分性及其数值模拟”（11301001）；安徽财经大学教研项目“数学建模竞赛引领大学生科研创新的研究”（acjyzd201429）。