基于虚拟同步发电机控制的VSC类同调等值方法

李承昱　许建中　赵成勇　刘　炜（新能源电力系统国家重点实验室（华北电力大学） 北京　102206）



基于虚拟同步发电机控制的VSC类同调等值方法

李承昱许建中赵成勇刘炜
（新能源电力系统国家重点实验室（华北电力大学） 北京102206）

针对含有采用虚拟同步发电机控制（VSG）策略的电压源型换流器（VSC）的电网，开展其局部的电磁暂态仿真等值方法研究。分析了VSC具有同步发电机特性后的功角特性在电网等值中的可行性。类比交流同调性判别的方法，设计了适合于VSC的类同调判据，提出了基于虚拟同步发电机控制的VSC参数聚合方法。在PSCAD/EMTDC仿真环境下搭建了基于虚拟同步发电机控制的VSC并联运行模型，划分了内部区域和外部区域。基于系统在单相接地故障扰动下各VSC的虚拟功角曲线，判断了其类同调性，划分了不同的类同调VSC群，并分别进行了参数聚合。最后对比了等值前、后的外部区域对内部区域的输出有功、无功曲线，误差分析结果表明等值前、后VSC群的潮流基本不变，从而验证了所提基于虚拟同步控制的VSC群类同调等值方法的正确性和有效性。

虚拟同步发电机VSC等值同调等值参数聚合

0　引言

随着化石燃料的逐渐枯竭，太阳能、风能等新能源的开发和利用越来越受到关注。一方面，新能源接逆变器并网，使得电网电力电子化，从而导致系统的惯量越来越小，而且这些新能源具有分散性和波动性，实现分布式能源平滑并网对逆变器控制提出了要求［1-3］。另一方面，随着大量逆变器接入电网，系统变得复杂，单纯依靠换流器提速模型［4］，不能应对超大规模含有逆变器电网的电磁暂态仿真需求。进行局部电网的VSC等值研究具有重要的理论和实际价值。

虚拟同步发电机（Virtual Synchronous Generator，VSG）控制是基于同步发电思想的新型的电压源型换流器（Voltage Source Converter，VSC）控制方法，具有很多传统VSC控制不具有的优势，应用场景广泛。它的提出使新能源并网逆变器具有了类似发电机外特性的性质，解决了传统VSC逆变器运行时输出阻抗小、阻尼小、无惯性等问题，提高了系统的稳定性［5］。文献［6］将这种能够模拟同步发电机的逆变器称为同步逆变器（synchronverter），该逆变器既可以并网工作，也可以单独工作，或者在没有外部通信的情况下并行工作。文献［7，8］优化了VSG控制的惯性参数和阻尼参数，并分析了VSG作为微电网中的微电源并网逆变器的优势。同步逆变器不仅能够用于太阳能［9］、风能等分布式发电［10-11］，还可以用于高压直流输电［12］、不间断电源并行运行等领域。另外，由于同步逆变器对电网可体现同步发电机特性，因此，一些用于同步发电机的经典控制策略也可以结合到同步逆变器控制中，以求可以达到更好的控制效果，一些经典的传统电网的分析方法便可用来分析这些含新能源并网的电力系统。由于VSG在新能源并网的诸多优势，可以预见其将成为新能源并网逆变器的主要控制方式之一［13，14］。

为了研究复杂系统安全稳定性和设计控制与保护方案，仿真分析必不可少。提高电磁暂态仿真效率，减小计算机计算负担，需要对复杂系统进行局部的等值简化。传统交流大电网系统中，同步发电机的动态等值研究已有很多，基于同调性的发电机动态等值与参数聚合得到了较广泛的应用［15-20］。随着电网中VSC逆变器的增多，VSC也将面临需要等值的问题。由于电网中VSC电磁暂态过程迅速，同调VSC判别困难，现有对VSC等值的研究几乎没有。仅有文献［21］通过微分几何理论，将功角同调的理论进行了拓展，提出了基于VSC的广义同调理论的概念。但文献［21］中所述的同调判断物理意义不直观，并且未对VSC参数聚合方法详细说明。

本文针对基于虚拟同步发电机控制的VSC，研究了电磁暂态仿真中逆变VSC的等值方法。介绍了虚拟同步发电机基本控制方式，结合交流系统中同步发电机的同调判别方法，提出了适合基于VSG控制的VSC类同调判据，基于同步发电机的转子运动方程机械特性，提出了类同调VSC控制参数和电路参数聚合方法。在PSCAD/EMTDC仿真环境下搭建了多台并联运行的基于VSG控制的VSC，观察了其同步发电机特性，并按照本文所提出的等值方法对其进行了类同调判别与参数聚合，对比了等值VSC群与原VSC群的运行效果与仿真效率。验证了所提等值方法的可靠性。

1　基于VSG控制的VSC结构和控制系统

1.1VSC与同步发电机机电模型的对应结构

典型的新能源并网逆变器拓扑结构如图1所示，逆变VSC经过LC滤波器之后与电网相联。图中虚线箭头也展示了虚拟发电机转矩与VSC拓扑结构的联系。VSG控制是利用同步发电机调节方式控制逆变器，使逆变VSC对外表现出同步发电机的特性。为了更好地说明本文研究的VSC等值方法的重点，下面将简单阐述虚拟同步发电机控制的基本原理［6］。

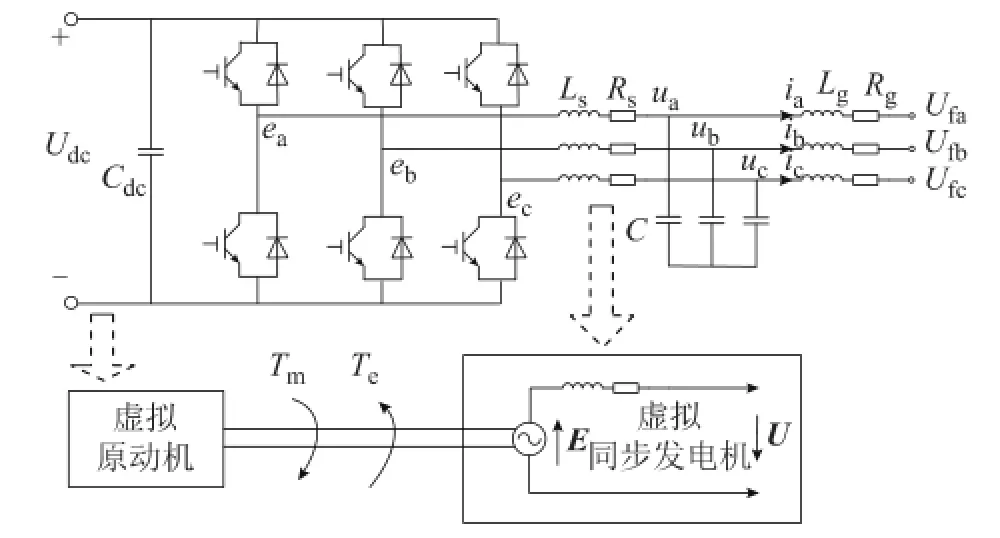
图1　VSC一般拓扑Fig.1　General VSC topology

1.2电磁部分模型

为了既满足电力系统分析的需要又不至于使控制器设计复杂，需要对同步发电机模型进行简化。假设采用的同步发电机模型转子为圆形，如图2所示。该同步发电机模型无阻尼绕组，每相有1对磁极，铁心没有饱和效应。定子三相绕组结构为相同的集中线圈，旋转对称，空间相隔120°电角度，其自感系数为L，互感系数为M，线圈阻抗为Rs。

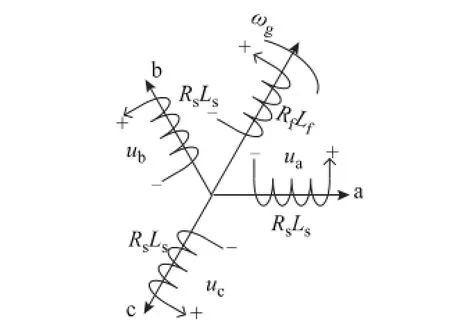
图2　理想三相隐极同步发电机结构Fig.2　Structure of an idealized three-phase round-rotor SG

令Ls=L+M，则同步发电机机端电压v= ［vavbvc］T，可表示为

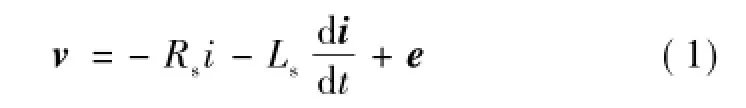
式中，e为同步发电机的三相感应电动势矢量，e= ［eaebec］T；i为发电机定子相电流矢量，i= ［iaibic］T。假设发电机励磁电流恒定，可以得到发电机感应电动势为

式中，Mf为定子绕组与转子绕组间的互感系数；if为励磁电流；ω为发电机转速。

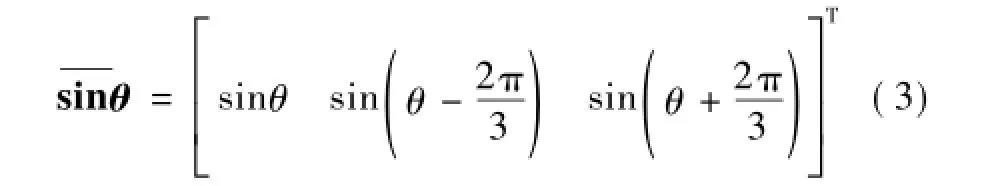
式（1）是发电机机端的表达式，联系图1的VSC结构，当改变式中各参数的定义，使得同步发电机的同步电感Ls与并网VSC的输出滤波电感Ls对应，同步发电机的同步电阻Rs与滤波电感和功率器件的等效电阻Rs对应，同步发电机的感应电动势e与VSC出口处电压输出电压e对应。可以发现它又与VSC输出的电压v表达式相同。这样就建立了VSC与同步发电机输出电压之间的联系。

1.3机械部分模型

同步发电机转矩方程可表示为

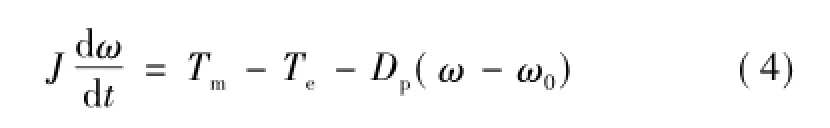
式中，J为转子转动惯量；Tm为机械转矩；Te为电磁转矩；ω为发电机机械角速度；ω0为同步角速度；本文中虚拟发电机为1对极，故机械角速度等于电角速度；Dp为阻尼系数。电磁转矩Te可表示为

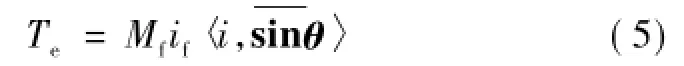
逆变VSC的直流侧电源为VSC提供能量，将其看作是虚拟原动机，并为VSC提供机械能。机械转矩结合1.2节所提的电磁部分，构成了一台虚拟同步发电机模型。为了使VSC具有发电机的机械转矩，对外表现出同步发电机转动的惯性与阻尼特性，需要在控制系统中进行改进来实现。

1.4VSG控制系统模型

虚拟同步发电机控制系统框图如图3所示。图3中，Pref为VSC的有功整定值；ωn为同步发电机的额定转速；Dp为阻尼系数；Dq为无功/电压下垂系数；i为abc三相相电流的反馈值；um为PCC点相电压峰值；ur为输出电压参考值。控制得到的结果由式（2）计算出VSC输出电压参考波，经过PWM调制驱动IGBT的开断。

图3　虚拟同步发电机控制系统框图Fig.3　Control strategy of the VSG

借鉴传统同步发电机通过对机械转矩的调节来调节发电机有功输出的原理，通过对虚拟同步发电机虚拟机械转矩Tm的调节来实现并网VSC有功指令的调节。

VSC无功控制加入了无功/电压Dq下垂系数，使得虚拟同步发电机无功调节与传统并网逆变器的无功控制策略不同，其在保证无功功率跟踪的同时，还能参与电网电压调节，根据电压的偏差为其接入的电网提供必要的无功支撑，具有了同步发电机的无功/电压下垂特性。

虚拟同步发电机控制在VSC中植入了同步发电机的机械转矩，使得并网VSC具有了同步发电机的特征，对外具有了功角特性。

2　基于VSG的VSC类同调等值

未来电网中新能源逆变并网数量增多，大量的电力电子元器件使得电网的分析控制表现出高阶非线性等特点。基于VSG控制的VSC具有同步发电机特性，是未来电网逆变器控制的发展趋势。可以借鉴交流系统中同步发电机的同调判别，对含有VSC的电网进行局部等值，化简网络结构，提高系统仿真效率，简化系统控制分析。

交流系统的同调等值分为5个步骤［15］:①划分研究系统区域和外部系统区域，等值过程保留研究系统区域，等值简化外部系统；②判断外部区域中同调发电机群；③对发电机母线化简合并；④网络化简；⑤发电机动态聚合，得到等值机参数。

本文阐述的VSC同调等值，步骤①、③、④与同步发电机的同调等值基本相同，在本文中不再赘述。重点将解决以上述步骤②和步骤⑤。虽然虚拟同步发电机具有了发电机的特性，在外部系统受到扰动后，VSC也具有了可观察的功角。但是VSC和同步发电机本质上存在差异，所以同调的判别依据需要做一定的修正，故在此称为类同调判别。

2.1VSC类同调判别

所谓同调就是当电力系统受到扰动以后，如果两台发电机功角差在给定时段内基本维持恒定，则认为这些发电机是同调的。实际系统中，功角差维持恒定很难满足，所以在实际应用中引入了同调机群的实用判据。用两台发电机相对于各自功角初值的Δδi、Δδj之差在给定时段t内的最大值来反映其同调程度，当其小于指定门槛值ε时，则称发电机是同调的，即满足［15］

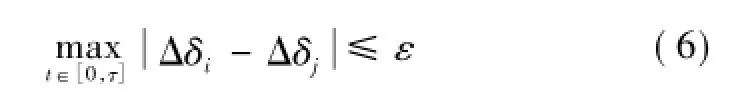
一般取τ=1～3 s，ε=5°～10°。VSC与同步发电机本质存在差异，直接套用该判据会导致同调VSC判别错误，从而影响等值效果。但是基于VSG控制的VSC被植入了同步发电机的转矩方程，在选取同调判据时，一定程度上又可以借鉴同步发电机与之对应的关系。

如图1所示，VSC直流侧所连接的电容是储能元件，这使得采用VSG控制技术的VSC中的电容储能Edc模拟了虚拟同步发电机转子转动所储存的机械能Ek，也使得VSC具有了惯性特征［22］。因此，可以得到二者的关系为

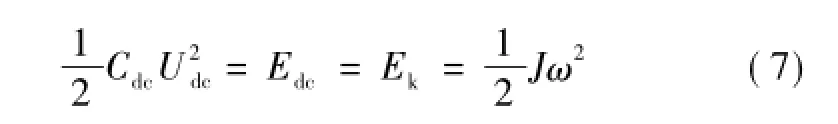
式中，Cdc为VSC直流侧电容；Udc为VSC直流电压。由式（7）可得出VSC的虚拟转动惯量JVSC与VSC参数的关系

由式（8）可知J在配电网或微网中的取值范围约为0.1～1 kg·m2。

交流系统同调等值判据中的τ，反映了在经历扰动后同步发电机功角变化时间，是同步发电机惯性时间常数的体现。同步发电机惯性时间常数 TSG表示为［23］

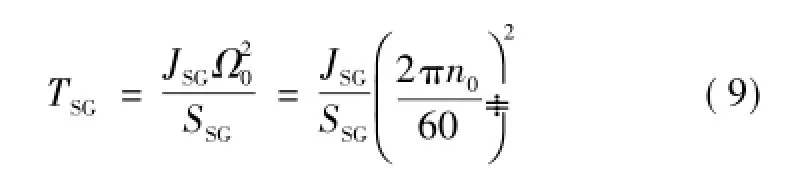
式中，JSG为同步发电机转动惯量，t·m2；SSG为同步发电机容量，kV·A；n0为同步发电机额定转速，取n0=3 000 r/min。水电机组的惯性时间常数一般为1～3 s，而火电机组的惯性时间常数为7～8 s［7］。

虚拟同步发电机有功控制环模拟了发电机的机械方程。文献［6］中根据虚拟同步发电机控制系统给出了其虚拟转动惯量时间常数为

在虚拟同步发电机控制中，为了使VSC体现同步发电机的调频功能，Dp选取也结合同步发电机频率/有功下垂特性，即

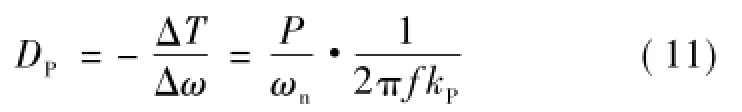
式中，kP为有功/频率下垂系数，其表征100%功率变化对应kP倍的频率变化。由式（11）可判断DP在配电网或微网中的取值约为1～10。用系数a表示同步发电机与基于VSG控制的VSC的惯性时间常数比值，即

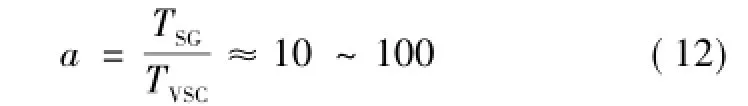
a值的大小体现了VSG控制的VSC与实际同步发电机时间常数的差异大小，参照这个差异，可以调整同调判据中时间的取值。根据对a值的估算，可以选取τ=0.1～0.6 s作为类同调的判断时间。从原理上看，基于VSG控制的VSC虽然具有同步发电机特性，但是暂态过程更快，在小干扰后更快进入稳态。相对同步发电机同调判据里选取较小的τ值使得类同调的VSC的判别更加迅速，减少了初始判断同调仿真的时间和计算量。考虑到选取的时间太短容易造成VSC类同调性误判的情况，本文选取τ值为0.4 s。

由式（8）可知，微电网中VSC的虚拟转动惯量较之同步发电机要小很多，J的取值范围也较小，故在门槛值ε选取时较同步发电机严苛。经过大量仿真，对于VSC类同调ε的选取范围为1°～5°。本文选取2°作为门槛值ε。在电磁暂态仿真中，每台VSC的Δδ可以精确测量，选取较小的ε使得类同调判别更加严苛，有利于减小等值误差。改写式（6）为

式中，t0为扰动加入时刻。若在所加扰动后，不同的基于虚拟同步发电机控制的VSC同时满足式（13），则称其为类同调VSC群。需要注意的是，虽然式（13）与式（6）形式一样，但是同调性判据门槛值的约束条件已经改变。

2.2类同调VSC参数聚合

对于类同调VSC的聚合，作如下假设:①类同调VSC具有相同的虚拟转速且都已转移到同一等值母线上；②聚合前、后，VSC输出的有功、无功保持不变；③类同调VSC群的控制参数和电路参数可以分别聚合。

因此，可以将类同调VSC参数聚合分为两个环节:类同调VSC群控制参数聚合和类同调VSC群电路参数聚合。

1）类同调VSC群控制参数聚合

VSC本身是不存在机械运动的，VSG控制赋予了VSC同步发电机的转子运动方程，从而对外显现出同步发电机的转子运动特性。第i台类同调VSC虚拟转子运动方程为

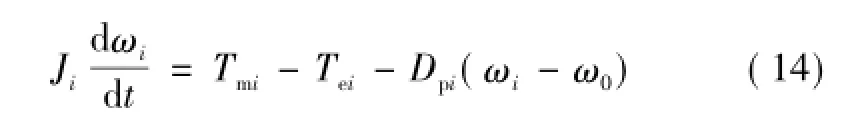
交流系统同步发电机等值时，转子运动方程的聚合是参数叠加，在转速ω相等时如式（15）所示。

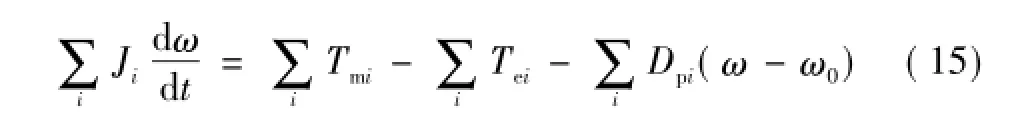
类同调的VSC控制器参数是虚拟转子运动方程的直接体现，所以类同调VSC控制参数聚合正好对应着传统同步发电机的转子运动方程聚合。在做转子运动方程的参数聚合时，为了保持其原来的虚拟转子运动特性，需要对控制系统中表征运动方程的部分控制参数进行叠加聚合。控制器各参数分步聚合方法如式（16）～式（19）所示。

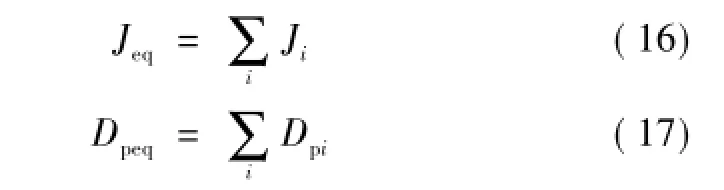
转矩的聚合约束条件为等值前、后输出的有功功率和无功功率不变，在控制其中体现为有功、无功的整定值的聚合，如式（18）、式（19）所示。

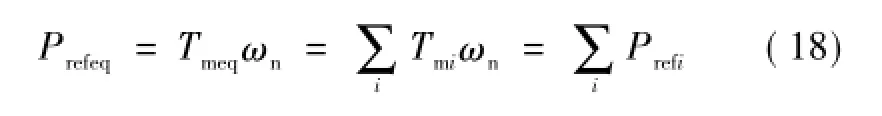
而控制器剩余的参数需要满足

结合电磁转矩表达式（式（5）），将剩余的控制参数聚合，可得

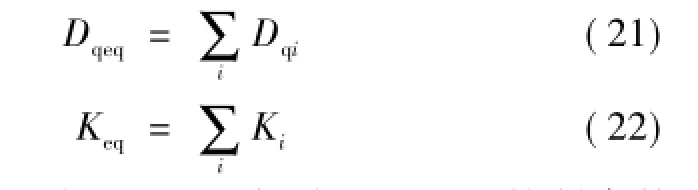
由上述过程可看出，对于类同调VSC的控制参数聚合是利用了虚拟同步发电机控制与同步发电机机械转矩的内在联系，最终体现为控制参数有名值叠加的过程。

2）类同调VSC群电路参数聚合

n台类同调VSC接在同一母线上电路结构如图4所示。需要将VSC的LCL滤波电路进行参数聚合。本文结合同步发电机电磁回路聚合方法来聚合VSC电路参数。

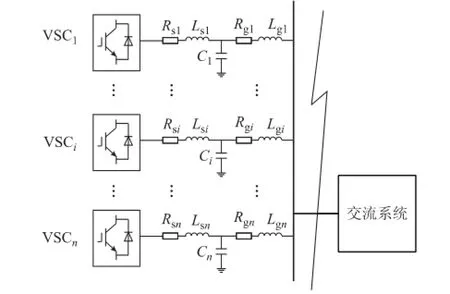
图4　并联VSC电路参数Fig.4　Circuit of parallel VSCs

其等值聚合过程可看作电路中各元件的并联等效，如式（23）～式（25）所示。

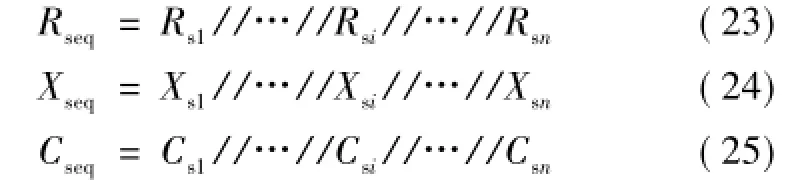
n台类同调VSC等值后的电路形式与单台VSC形式保持一致，电路参数即为所求的等值参数。本文运用的聚合方法简单且易实行，非常适合含大规模虚拟同步发电机并网等值聚合的情况。

3　仿真验证

为了验证本文所提的基于虚拟同步发电机的VSC类同调等值方法的正确性，在PSCAD中搭建5台参数不同的基于虚拟同步发电机控制的VSC，并联在同一交流母线A上运行。为了研究需要，假设母线A作为内部区域和外部区域的分界线。母线A的交流系统侧为内部系统，VSC侧为外部区域。在保证内部系统关键电气量仿真精度的前提下，简化网络拓扑，提高电磁暂态仿真效率，同时突出研究重点，需要对外部区域进行等值处理，如图5所示。

图5　仿真系统结构Fig.5　The simulation system structure

3.1原始系统参数

系统参数和各台VSC参数见表1、表2。参数选取了微网级别的换流器参数，符合目前微电网中大量分布式电源并网的应用场景。本文所提出的VSC类同调等值方法与交流系统的同调等值类似，该方法应用场合与电压等级、容量无关，虽然是在低压微网系统中进行验证，但也适用于微网或高压输电网中容量相差不大的VSC之间的等值，并可推广到以后大电网中大规模新能源并网等值的情况。

表1　系统参数Tab.1　Parameters of grid

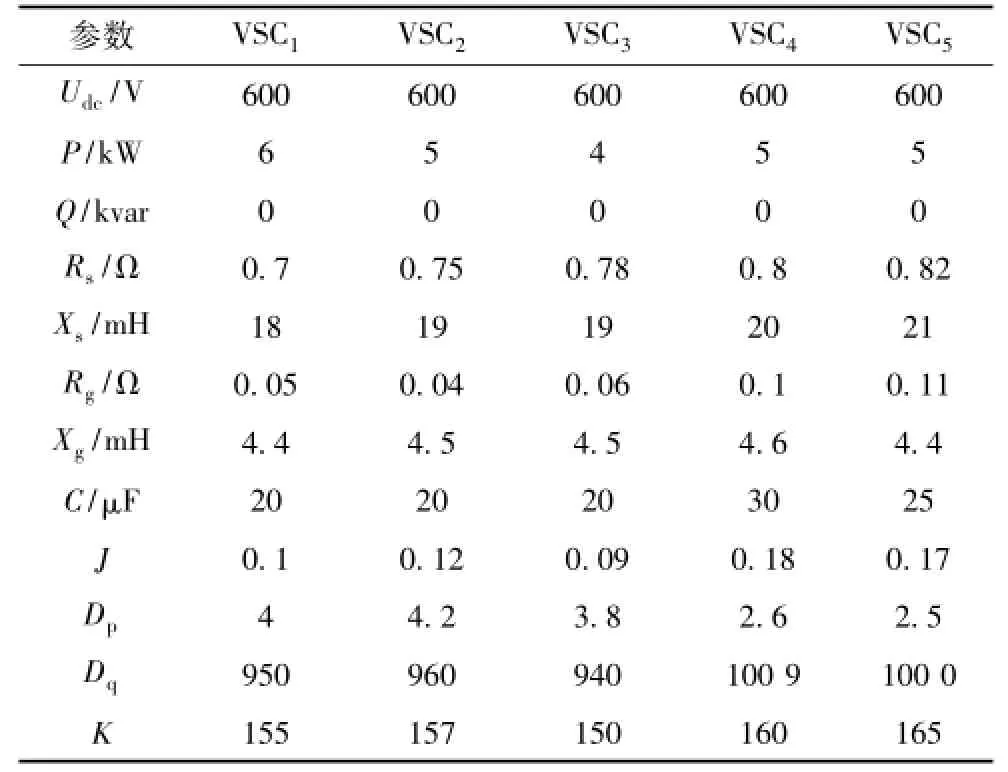
表2　基于虚拟同步发电机控制的VSC参数Tab.2　Parameters of VSG-based VSCs

表2中各VSC的电路参数、控制参数名称分别与图1和图3对应。

3.2VSC类同调判别及参数聚合

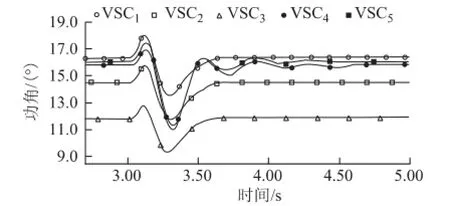
图6　扰动后各VSC虚拟功角曲线Fig.6　Virtual power angle curve of each VSC

在仿真中，起始时刻至3.0 s，5个VSC站都达到稳定运行状态。3 s时在图5中的F点处设置A相单相接地短路故障，接地电阻为0.1 mΩ。0.05 s后故障消除。在此过程中，由于状态发生了改变，因此造成了系统的一个小扰动。通过仿真可以得到VSC1～VSC5的功角曲线如图6所示。需要指出的是，基于虚拟同步发电机控制的VSC功角是VSC出口电压相角减去端口电压相角。相角的求取采用的是PLL锁相环，而PLL得到的相角会在相角达到360°后跳变到0°，这使得相角做差时，当超前的相角发生周期性跳变时，功角结果将出现尖峰。为了获得准确的功角特性曲线，本文对此周期性跳变进行了数据处理。

由图6可以看出，VSC1、VSC2和VSC3虚拟功角曲线变化规律一致，VSC4和VSC5虚拟功角曲线变化规律一致。提取数据进行相对虚拟功角计算，结果见表3。该表格中下三角数据与上三角数据对称，在此只列出上三角的数据。

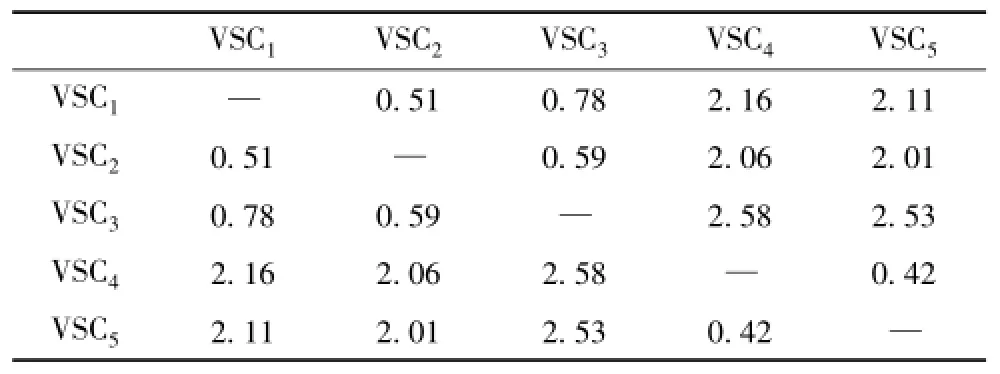
表3　相对虚拟功角Tab.3　Relation of virtual power angle（单位:°）

VSC1、VSC2和VSC3之间相互满足式（13）的VSC类同调判据，VSC4和VSC5之间满足类同调判据。可以将这5台VSC分为两个类同调群，分别进行等值工作。按照本文第 2.2节提出的参数聚合方法，将VSC1、VSC2和VSC3等值为一台VSC，命名为VSC_A，将VSC4和VSC5等值为一台VSC，命名为VSC_B，如图5所示。等值和参数聚合后VSC_A和VSC_B的参数见表4。

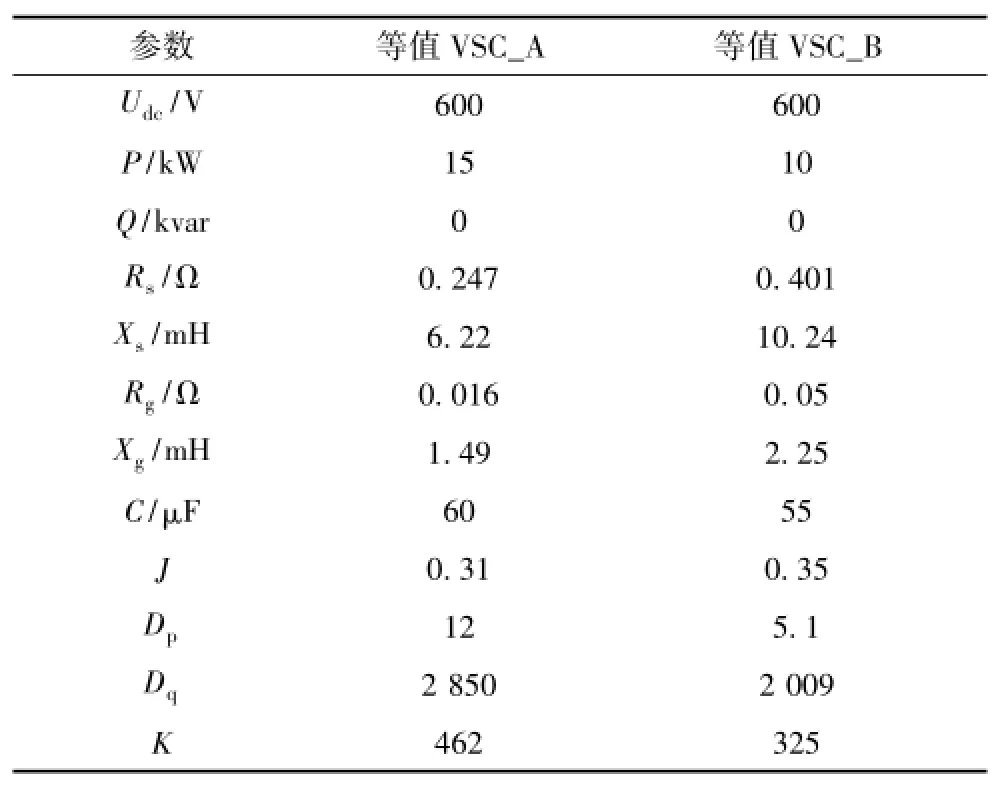
表4等值VSC参数Tab.4　Parameters of equivalent VSC

3.3等值VSC仿真验证

1）算例1:两台类同调VSC等值

为了排除等值后VSC_A和VSC_B之间的互相影响引起的等值误差，本文将首先单独验证 VSC4和VSC5等值为VSC_B的情况。仿真系统仍然如图5所示，只是删除了1、2和3号VSC。设置了3.1节所述相同的故障扰动，对比等值前后内部区域和外部区域分界线处E的有功、无功功率，结果如图7和图8所示。同时观察VSC4、VSC5和VSC_B在相同扰动下的虚拟功角曲线，其结果如图9所示。

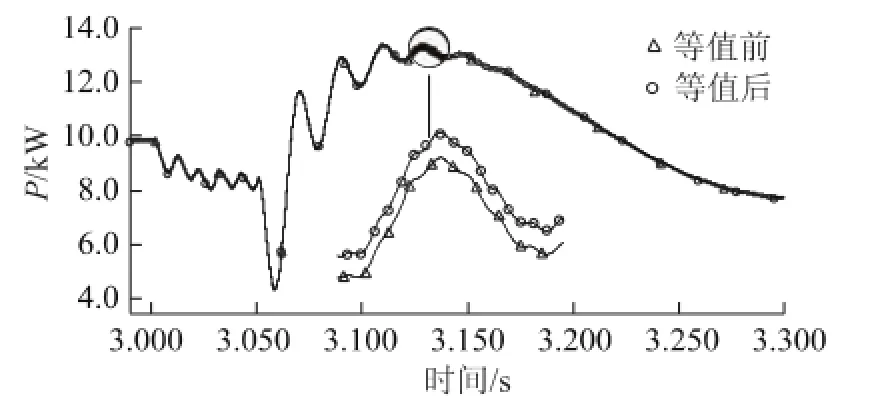
图7　原VSC与等值VSC有功功率对比Fig.7　Comparison of active power between detailed VSCs and equivalent VSC

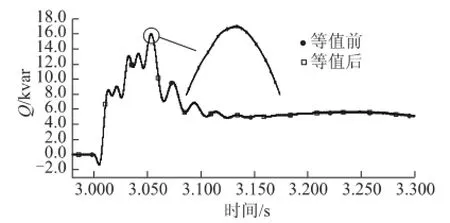
图8　原VSC与等值VSC无功功率对比Fig.8　Comparison of reactive power between detailed VSCs and equivalent VSC

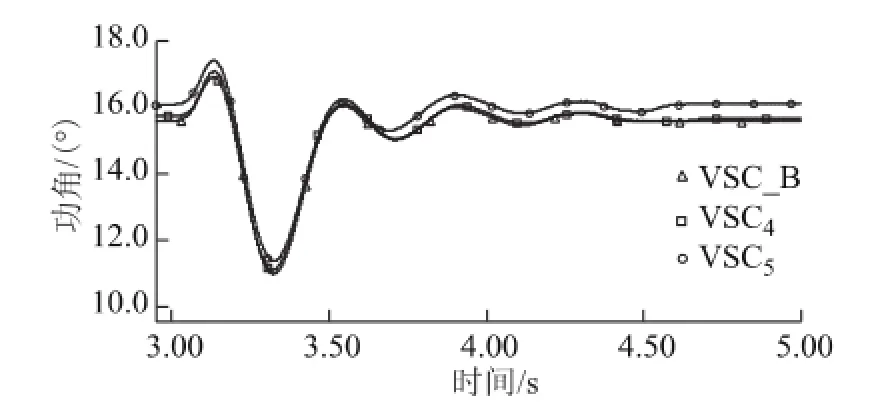
图9　VSC4、VSC5与VSC_B虚拟功角对比Fig.9　Comparison of virtual power angle between VSC4VSC5and VSC_B

由图7和图8可以看出，在VSC出口发生单相接地故障后，输出有功功率跌落，由于VSG控制的惯性作用，跌落得较缓慢。由于母线A电压的跌落，VSG控制中的无功/电压下垂控制发生作用，向系统输出无功功率提供交流电压支撑。等值前后，有功功率曲线和无功功率相似度很高。提取数据分析可得有功功率暂态过程平均误差为0.5%，最大误差为1.3%。无功功率暂态过程平均误差为0.2%，最大误差为0.9%。等值之后有功、无功的误差很小，该仿真误差在电网分析可接受的误差范围之内。

由图9可知，等值后的VSC_B的虚拟功角曲线和VSC4、VSC5的虚拟功角曲线变化趋势一致，其相对虚拟功角值计算结果满足式（18）。说明 VSC_B与VSC4、VSC5属于类同调VSC。该结果说明了等值后VSC_B较好地保留了外部区域VSC4和VSC5的动态特性，说明将两台类同调VSC并联运行等值成一台等效VSC是可行的，同时也初步验证了本文所提出的类同调等值方法的有效性。

2）算例2:两个类同调VSC群同时等值

接下来验证5台VSC分为两个类同调群等值为两台等值VSC运行的情况。同样设置了3.1节所述的相同故障扰动，对比等值前后图5中内部区域和外部区域分界线E处的有功、无功功率，同时观察VSC_A和VSC_B在相同扰动下的虚拟功角曲线，其结果如图10～图12所示。

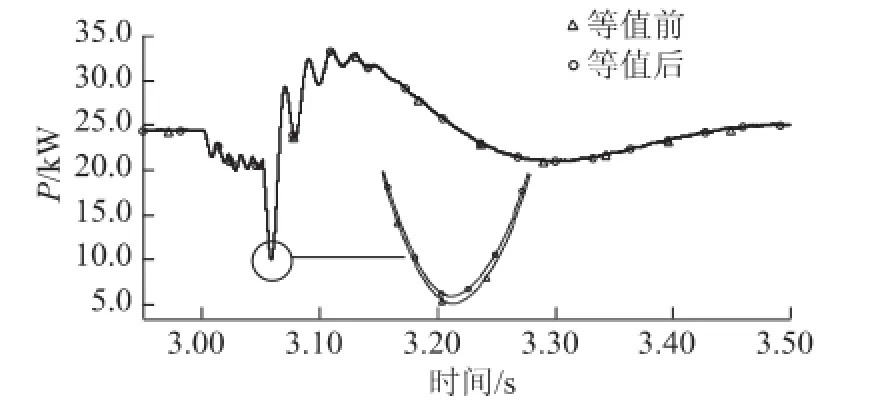
图10　原VSC与等值VSC有功功率对比Fig.10　Comparison of active power between detailed VSCs and equivalent VSC

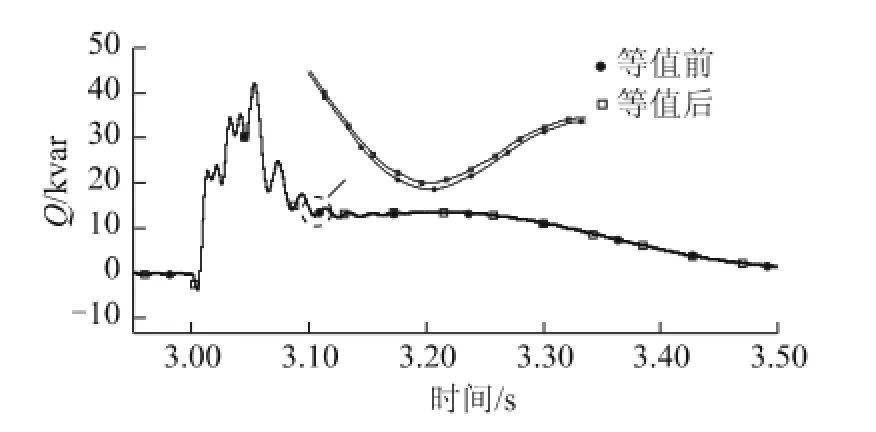
图11　原VSC与等值VSC无功功率对比Fig.11　Comparison of reactive power between detailed VSCs and equivalent VSC

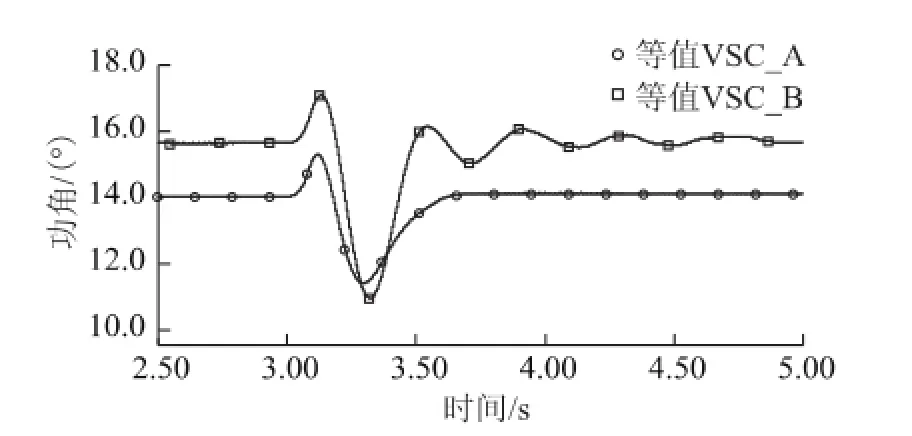
图12　VSC_A与VSC_B虚拟功角对比Fig.12　Comparison of virtual power angle between VSC_A and VSC_B

提取图10和图11中的数据进行分析，可以得到有功功率暂态过程平均误差为0.16%，误差最大值为0.44%。无功功率暂态过程平均误差为0.2%，误差最大值为0.72%。等值后的系统对外潮流没有变化，且等值前后暂态过程有功、无功数据非常接近。5台VSC分为两个类同调群等值为两台VSC后，较之两台类同调VSC等值一台VSC的情况，功率误差百分比并没有放大，说明了本文提出的等值方法在多个类同调群等值中的正确性。

从图12可以看出，等值后VSC_A的虚拟功角曲线与原VSC1、VSC2和VSC3在相同扰动下变化趋势一致，VSC_B的虚拟功角曲线与原VSC4、VSC5变化趋势一致，没有畸变的动态特性。按式（13）计算得到VSC_A和VSC_B的相对相角差为2.4°。等值前不同调的VSC组成各自的类同调群后进行等值，对应等值后不同的单台VSC仍然不符合类同调判据，保留了原有的动态特性，因此等值后的系统可以无误地进行后续的稳定性分析等研究。

4　结论

本文针对基于同步发电机控制的VSC开展了等值方法研究。类比交流同调判别方法设计了VSC类同调判据，提出了基于虚拟同步发电机控制的VSC参数聚合方法，得到如下结论:

1）本文提出的较小的同调判别值使得类同调的VSC的判别更加迅速，加法聚合的方法聚合了类同调VSC群的控制器参数。结合同步发电机电磁回路聚合方法，聚合了类同调VSC组的电路参数。所采用的聚合方法简单易实行，适合于含大规模虚拟同步发电机逆变器并网等值聚合的场景。

2）在PSCAD中搭建了含五台具有虚拟同步发电机特性VSC并联运行的系统，依据提出的VSC类同调判据，分别将其等值为两个类同调VSC群并进行了参数聚合。电磁暂态仿真结果表明等值误差在2%以内，验证了本文所提出等值方法的正确性。

3）针对具有很强可控性且本身不具备功角特性的VSC，本文提出了基于虚拟同步发电机控制的VSC类同调等值方法，为新能源经VSC并网的系统提供了等值思路。为了使该方法具有更广泛的应用前景，研究VSC群与传统机组的混合同调等值，以及将VSC等值推广到模块化多电平换流器的等值，具有重要的实际意义。

［1］刘杨华，吴政球，涂有庆，等.分布式发电及其并网技术综述［J］.电网技术，2008，32（15）:71-76.

Liu Yanghua，Wu Zhengqiu，Tu Youqing，et al.A survey on distributed generation and its networking technology［J］.Power System Technology，2008，32 （15）:71-76.

［2］孟建辉，石新春，王毅，等.改善微电网频率稳定性的分布式逆变电源控制策略［J］.电工技术学报，2015，30（4）:70-79.

Meng Jianhui，Shi Xinchun，Wang Yi，et al.Control strategy of DER inverter for improving frequency stability of microgrid［J］.Transactions of China Electrotechnical Society，2015，30（4）:70-79.

［3］朱旋，陈得宝，方振国，等.平均成本下垂控制策略在分布式发电中的应用［J］.电力系统保护与控制，2015，43（10）:14-20.

Zhu Xuan，Chen Debao，Fang Zhenguo，et al.Mean cost-based droop scheme in the application of distributed generators［J］.Power System Protection and Control，2015，43（10）:14-20.

［4］Xu J，Gole A M，Zhao C.The use of averaged-value model of modular multilevel converter in DC grid［J］. IEEE Transactions on Power Delivery，2015，30（2）: 519-528.

［5］张玉治，张辉，贺大为，等.具有同步发电机特性的微电网逆变器控制［J］.电工技术学报，2014，29 （7）:261-268.

Zhang Yuzhi，Zhang Hui，He Dawei，et al.Control strategyofmicrogridconverterswithsynchronous generatorcharacteristic［J］.TransactionsofChina Electrotechnical Society，2014，29（7）:261-268.

［6］Zhong Q C，Weiss G.Synchronverters:inverters that mimic synchronous generators［J］.IEEE Transactions on Industrial Electronics，2011，58（4）:1259-1267.

［7］吕志鹏，盛万兴，钟庆昌，等.虚拟同步发电机及其在微电网中的应用［J］.中国电机工程学报，2014，34（16）:2591-2603.

Lü Zhipeng，Sheng Wanxing，Zhong Qingchang，et al. Virtual synchronous generator and its applications in micro-grid［J］.Proceedings of the CSEE，2014，34 （16）:2591-2603.

［8］孟建辉，王毅，石新春，等.基于虚拟同步发电机的分布式逆变电源控制策略及参数分析［J］.电工技术学报，2014，29（12）:1-10.

Meng Jianhui，Wang Yi，Shi Xinchun，et al.Control strategy and parameter analysis of distributed inverters based on VSG［J］.Transactions of China Electrotechnical Society，2014，29（12）:1-10.

［9］MingWL，ZhongQC.Synchronverter-based transformerless PV inverters［C］//40 th Annual Conference of the IEEE on Industrial Electronics Society，Dallas，2014:4396-4401.

［10］Sakimoto K I，Sugimoto K，Shindo Y.Low voltage ride through capability of a grid connected inverter based on the virtual synchronous generator［C］//10 th International Conference on IEEE Power Electronics and Drive Systems，Kitakyushu，Japan，2013:1066-1071.

［11］王思耕，葛宝明，毕大强.基于虚拟同步发电机的风电场并网控制研究［J］.电力系统保护与控制，2011，39（21）:49-54.

WangSigeng，GeBaoming，BiDaqiang.Control strategies of grid-connected wind farm based on virtual synchronous generator［J］.Power System Protection and Control，2011，39（21）:49-54.

［12］AouiniR，MarinescuB，BenKK，etal. Synchronverter-based emulation and control of HVDC transmission［J］.IEEE Transactions on Power Systems，2015，31（1）:1-9.

［13］吴轩钦，谭国俊，何凤有，等.变频驱动系统电网接口虚拟同步发电机［J］.电工技术学报，2015，30 （23）:83-92.

Wu Xuanqin，Tan Guojun，He Fengyou，et al.Virtual synchronous generator control scheme of grid interface for variable frequency drive systems［J］.Transactions of China Electrotechnical Society，2015，30（23）:83-92.

［14］ 张武其，吕洋.向弱电网供电的VSC-HVDC系统的模拟惯量控制策略研究［J］.电力系统保护与控制，2016，44（6）:104-110.

Zhang Wuqi，Lü Yang.Emulation inertia control strategy for VSC-HVDC supplying weak network［J］.Power System Protection and Control，2016，44（6）:104-110.

［15］ 倪以信，陈寿孙，张宝霖.动态电力系统的理论和分析［M］.北京:清华大学出版社，2002.

［16］ 杨靖萍.大规模互联电力系统动态等值方法研究［D］.杭州:浙江大学，2007.

［17］Kim S，Overbye T J.Enhanced measurement-based dynamicequivalenceusingcoherencyidentification ［C］//IEEE Power and Energy Conference，Illinois，2013:200-205.

［18］ 李光辉.面向实时仿真的大规模交直流混联电网动态等值研究［D］.上海:上海交通大学，2013.

［19］Zhang Baozhen，Zhang Yao，Liao Mingyang，et al. Study on dynamic equivalent coherency-based of Hainan power grid［C］//2012 Asia-Pacific Power and Energy Engineering Conference，Shanghai，2012:1-4.

［20］ 张元，郝丽丽，戴嘉祺.风电场等值建模研究综述［J］.电 力 系 统保 护 与 控 制，2015，43（6）: 138-146.

Zhang Yuan，Hao Lili，Dai Jiaqi.Overview of the equivalent model research for wind farms［J］.Power SystemProtectionandControl， 2015，43（6）: 138-146.

［21］ 查晓明，张扬，成燕，等.用于简化微电网结构的微分几何广义同调方法［J］.电工技术学报，2012，27（1）:24-31.

Zha Xiaoming，Zhang Yang，Cheng Yan，et al.New method of extended coherency for micro-grid based on homology in differential geometry［J］.Transactions of China Electrotechnical Society，2012，27（1）:24-31.

［22］Remon D，Cantarellas A M，Rakhshani E，et al.An activepowersynchronizationcontrolloopforgridconnected converters［C］//IEEEPowerandEnergy Society General Meeting，Washington，2014:1-5.

［23］ 常鲜戎，赵书强.电力系统暂态过程［M］.北京:机械工业出版社，2010.

李承昱男，1991年生，博士研究生，研究方向为柔性直流输电。

E-mail:lichengyu0216@foxmail.com（通信作者）

许建中男，1987年生，博士，讲师，研究方向为柔性直流输电。

E-mail:xujianzhong@ncepu.edu.cn

Coherency Equivalence Method for Voltage Source Converter Based on Virtual Synchronous Generator

Li ChengyuXu JianzhongZhao ChengyongLiu Wei
（State Key Laboratory of Alternate Electrical Power System With Renewable Energy Sources North China Electric Power UniversityBeijing102206China）

This research is focusing on conducting partial equivalence method for the power grid which operates with voltage source converter（VSC）based on the virtual synchronous generator（VSG）control strategy.The feasibility of applying power grid equivalence method in VSC with synchronous generator power-angle characteristic features has been analyzed.Then，on the analogy of AC coherency-based method，a VSC type coherency criterion has been designed and a VSC parameter aggregation method based on virtual synchronous generator control has been put forward.Under PSCAD/EMTDC simulated environment，VSCs parallel operation model is built based on virtual synchronous generator control.This system is divided into internal area and external area.Based on the virtual power-angle curve after single-phase ground fault disturbance，the VSCs coherency is judged and divided them into different coherent groups.Each group is proceeded parameter aggregation respectively.Finally，the output curve of active and reactive power from external area to internal area is chosen as object.Based on comparing the output curve before and after equivalence，the error analysis result indicates that the power flow is invariant during the equivalence.This validates the correctness and effectiveness of the referred coherency equivalence method.

Virtual synchronous generator，VSC equivalence，coherency equivalent，parameter aggregation

TM74

国家自然科学基金（51177042）、国家高技术研究发展（863）计划（2013AA050105）和中央高校基本科研业务专项资金（2015XS08）资助项目。

2015-06-23改稿日期 2015-11-05