数学模型与数学分析
——怎样解答“盈亏问题”
2016-08-10邓忠洪
邓忠洪
(四川省资阳市雁江区第七小学)
数学模型与数学分析
——怎样解答“盈亏问题”
邓忠洪
(四川省资阳市雁江区第七小学)
平时学生不会做数学题时,我们有的老师总认为学生没读懂题,让学生反复读题。殊不知,你让学生按语文的读题方法去读,哪怕他读上一千遍一万遍,他做不来还是做不来。数学的建模与分析非常重要,有了规范的数学模型,就能正确地进行数学分析。只有明确了题目中各种信息及问题间的数量关系,才能正确迅速地解决较难的数学问题。笔者以“盈亏问题”的解题方法为例,谈谈怎样建立数学模型和进行数学分析。
一、他人的经验及方法
把一定数量的物品平均分给一定数量的人,每人少分,则物品有余(盈);每人多分,则物品不足(亏)。已知所盈和所亏的数量及两次每人所分的数量,求人数的应用题叫盈亏问题。
盈亏问题的基本解法是:份数=(盈+亏)÷两次分配数的差;
物品总数=每份个数×份数±盈亏数。
解答盈亏问题的关键是要求出总差额和两次分配的数量差,然后利用基本公式求出分配人数,进而求出物品的数量。
趣味数学之《木长几何》——《孙子算经》里有这样一道题:今有木,不知长短。引绳度之,余绳四尺五,屈绳量之,不足一尺。木长几何?(屈绳的意思是把绳子对折,度是量的意思,四尺五是4.5尺)
分析:用绳量木,绳子多出4.5尺,把绳对折再量,绳子又短1尺,可推出单股绳子比对折起来长5.5尺,多出的5.5尺正好是绳子的一半(如图)。
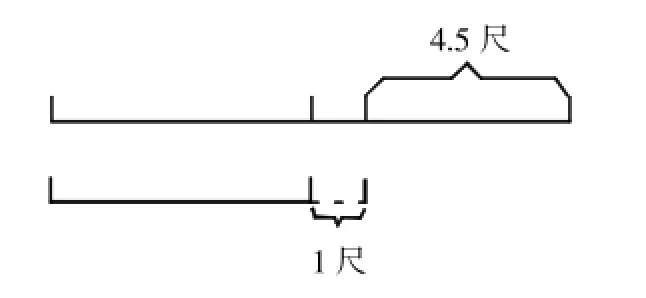
解答:绳子的长度:(4.5+1)×2=11(尺)
木料的长度:11-4.5=6.5(尺)
答:(略)
分析中,“用绳量木,绳子多出4.5尺,把绳对折再量,绳子又短1尺,可推出单股绳子比对折起来长5.5尺。”这里用到了一点点“盈亏问题”。为什么这样说呢?遇到类似问题还能用这种方法解答吗?请关注下面的内容。
二、建立数学模型
他人的方法及经验看似简单易行,可事实并非如此。学生机械地套用公式,并不完全理解解题思路,题目稍加变化,他们又束手无策了。
笔者引导学生先分析并找出“盈亏问题”的特点——它就是两种有余数的除法,再根据有余数除法各部分间的关系,建立“盈亏问题”总的数学模型:
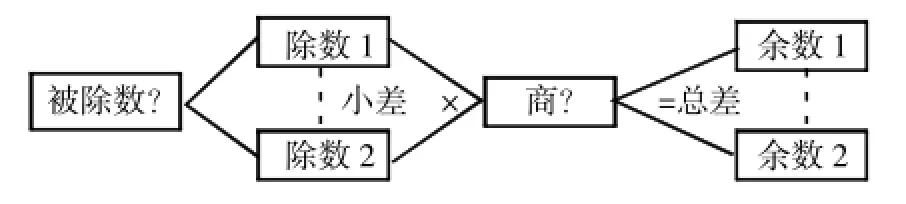
“盈亏问题”总的数学模型中两次被平均分的总数——被除数是一定(不变)的;平均分的标准不同,我们归纳为两种,即除数1和除数2;分得的结果中的份数——商也是一定(不变)的,分得的结果中的余数——盈亏数则不同,我们把它们分别定义为余数1和余数2。当被除数和商不变时,除数变大,余数则会变小,反之。
两次分得的余数之间的差,我们把它定义为“总差”,两次平均分的标准之间的差,我们把它定义为“小差”。正因为有分得的结果之一“商”那么多个“小差”才汇成最后结果之二“余数”间的“总差”,即“小差×商=总差”。于是,关键问题“商”就得到解决:商=总差÷小差。
如“幼儿园买来一些玩具,如果每班分7个玩具,则多出2个玩具;如果每班分10个玩具,则差13个玩具,幼儿园有几个班?这批玩具有多少个?”的数学模型:

三、进行数学分析
根据建好的数学模型,我们进行“盈亏问题”的数学分析:
第二种分法的总个数比第一种分法的总个数多(2+13)个为“总差”,第二种分法比第一种分法每班多分(10-7)个为“小差”,每班多分的“小差”乘班数就等于最后的“总差”。由此可以求出幼儿园共几班这个关键问题。
这个幼儿园有(2+13)÷(10-7)=5(班)
求出了模型中的商,再根据有余数的除法中“被除数=商×除数+余数”就可求出这批玩具共有多少个了。
这批玩具有7×5+2=37(个)或10×5-13=37(个)
答:(略)
四、适时推广应用
我们通过建立数学模型和进行数学分析,掌握了“盈亏问题”的解题方法,适当增加难度,加以推广应用。
1.用一根长绳测量井的深度,如果绳子两折时,多5米,如果绳子三折时,差1米。求绳子长度和井深。(提示:绳子两折即把绳子平均分成两份,三折即三股。)
社区教育传承与创新非物质文化遗产的活动主体多为各级政府部门、驻社区机构、公共服务机构、企事业单位、社区居民、学校及其他教育机构等,但各部门的责任分工还不够细化明确。尽管一些院校开展了非物质文化遗产的教育工作,设置了相关课程,但仍存在不专业现象。比如艺术院校将原本的设计艺术学专业设置为“传统工艺美术”,将原本的戏曲文学专业设置为“传统戏曲”等,但这些课程所涉及的内容往往学科化有余,传统性传承性不足,而且,非物质遗产的中、高等教育有待健全[7]。此外,企业组织机构及其他社会力量的参与度并不够,也在很大程度上限制了活动的灵活性和影响力,达不到应有的社会效应。
很明显,该题不能用“他人的经验及方法”之《木长几何》的方法来进行解答。而《木长几何》题目却能用“盈亏问题”的模型来进行分析和解答。
2.小宏从家到校上学,出发时他看看表,发现如果每分钟步行80米,他将迟到5分钟;如果先步行10分钟后,再改成骑车每分钟行200米,他就可以提前1分钟到校。问小宏从家出发时离上学时间有几分钟?
观察分析,这两题都属“盈亏问题”,只是题中的“盈亏(余数)”不是现成的,需要首先求出。
第1题的数学模型及数学分析:

井深:(5×2+1×3)÷(3-2)=13(米)
绳长:2×13+5×2=36(米)或(13+5)×2=36(米)答:(略)
《木长几何》数学模型及数学分析:
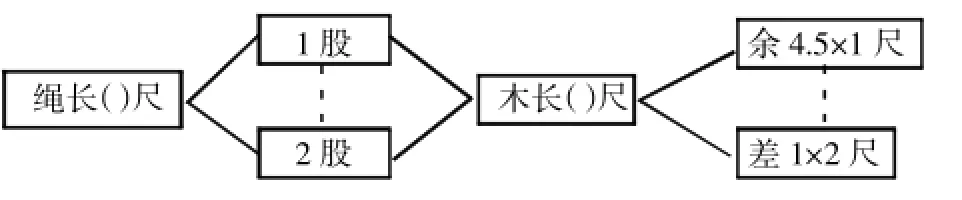
木长:(4.5×1+1×2)÷(2-1)=6.5(尺)
绳长:6.5+4.5=11(尺)或(6.5-1)×2=11(尺)
答:(略)
通过比较《木长几何》的两种方法,我们发现,他人的经验及方法具有局限性,只能用于特例;而我们的“盈亏问题”模型具有通用性,只要是“盈亏问题”都能用它来解答。
第2题的数学模型及数学分析——
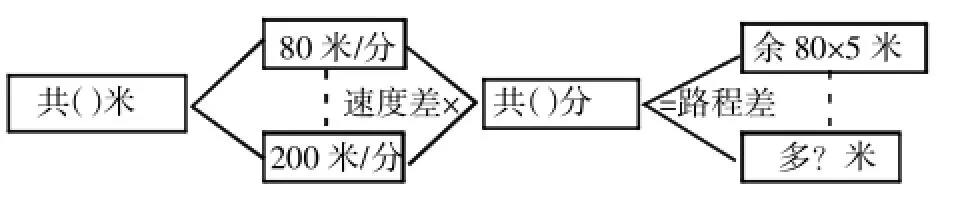
“余数1”:80×5=400(米)
求“余数2”步骤多一些。
①10分钟的步行改成骑车要提前:10-80×10÷200=6(分)
②假如他骑车一直骑到上学时间到时会多行:200×(6+1)= 1400(米)
“余数2”也可:(200-80)×10+200×1=1400(米)
小宏从家出发时离上学有:(400+1400)÷(200-80)=15(分)
答:(略)
我相信,只要坚持让学生按数学模型来读题、抄题,数学分析就更加容易和明了,他们就会更好地解决各种数学难题。
何升根.也谈“一类盈亏问题的解法”[J].小学教学参考:教学版,2006(35):45.
·编辑段丽君
