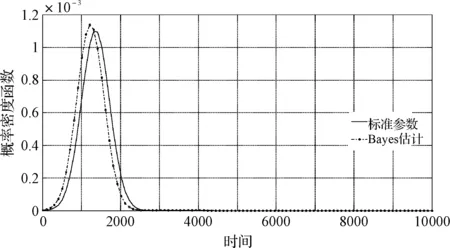
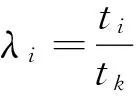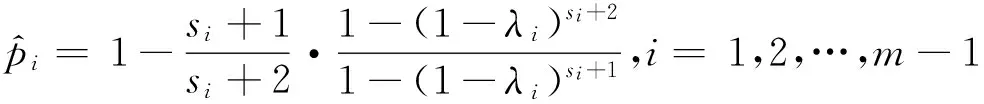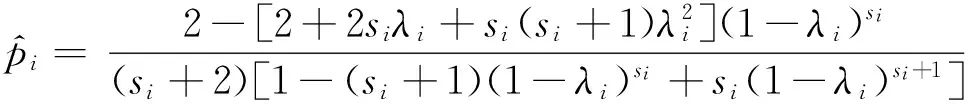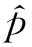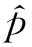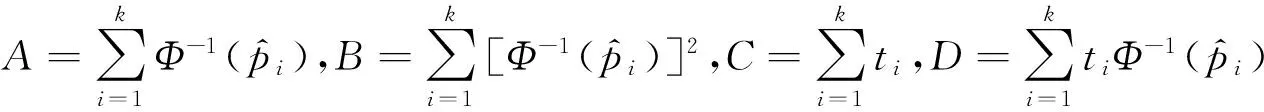正态型部件的参数估计方法研究*

陆洪武　邵松世

(1.海军装备部信息系统局　北京　100000)(2.海军工程大学科研部　武汉　430033)



正态型部件的参数估计方法研究*

陆洪武1邵松世2

(1.海军装备部信息系统局北京100000)(2.海军工程大学科研部武汉430033)

摘要针对正态型部件的参数估计问题，在极大似然估计和Bayes估计的一般计算方法基础上，结合装备使用数据给出了正态分布两种参数估计方法的计算流程，重点分析了只有一个失效数据情况下Bayes估计方法计算的准确性和先验信息对计算结果的影响，并研究了多个失效数据情况下的处理方法。通过算例分析，说明了Bayes估计对正态型部件参数估计的准确性和适用性。

关键词正态型部件; 极大似然估计; Bayes估计; 先验信息; 参数估计

Class Number

1引言

正态型部件作为一种常见的寿命分布类型，广泛存在于舰船机械类装备中[1～2]。对该类型寿命分布参数估计的准确与否将直接影响部件的可靠性分析、备件供应规划决策等后续保障性工作[3～5]。因此，准确估计这些参数值显得尤为重要。

极大似然估计是一种经典估计方法，其优点是具有较好的大样本性质，并符合人们的直观印象，缺点是小样本情况无法准确的估计出参数的真值;贝叶斯估计与极大似然估计的不同之处在于利用了先验信息，即历史信息，其优点是在样本信息较少的情况下能够较准确的给出未知参数的估计值，其缺点是先验信息较难获得。针对这两种参数估计方法，相关专家学者进行了深入的研究，如文献[6]给出了不同寿命分布型产品的极大似然估计方法;文献[7]介绍了当产品寿命分布为指数分布，且样本数据为分组型时参数的Bayes 估计方法;文献[8]给出了当寿命分布为正态分布时，产品失效概率的Bayes估计方法;文献[9]给出了当产品寿命分布为正态分布时，在均值未知，方差已知情况下的均值Bayes估计问题，但是在实际计算中，正态分布的方差值也是很难获得的。

总的来说，极大似然估计和Bayes估计是进行寿命分布参数估计比较常用的方法，相关专家学者对这两类方法进行了深入的研究，但是将这两种方法结合装备保障的现场数据进行运用的研究较少。另一方面，两种参数估计方法各有优缺点，在分析装备的实际使用数据时，选择何种方法进行寿命分布类型部件的参数估计也是一个问题。本文从这两个问题出发，针对正态型部件，首先介绍极大似然估计和Bayes估计的总体思路，进一步分析在已知寿命分布类型情况下，对寿命分布参数进行估计的具体方法。在此基础上，重点分析Bayes估计在装备使用数据下的应用。

2极大似然估计

设产品寿命服从正态分布，则其概率密度函数为[10]

其中，μ为均值，σ为方差。正态分布概率密度函数的似然函数表达式可写为

(1)

转换为负对数似然函数为

(2)

使L取最大值或最小值的参数满足下式：

得

(3)

(4)

分别解式(3)、(4)得μ、σ2的极大似然估计值为

(5)

(6)

其中，ti为失效前工作时间。

使用极大似然估计进行计算前提是计算数据均为完全无删失数据，在装备实际使用过程，采集的数据大部分为定时截尾或定数截尾数据，采集完全无删失数据基本不可能，所以此方法的适用性受到很大限制。

3Bayes估计

对于非指数型部件来说，利用Bayes估计方法进行参数估计较为复杂。对于新列装的装备或高可靠性部件来说，故障信息为小子样信息，通过观察装备的实际使用数据，很多部件的故障只发生一次，即失效数据只有一个(简记为DOOF数据[8])。因此，利用DOOF数据研究正态型、威布尔型等非指数型部件的参数估计，有较大的实际意义和应用范围。在对μ,σ2进行参数估计时，由于两个参数均为未知参数，直接对两参数进行Bayes估计涉及多参数模型，模型复杂，且先验分布及超参数难以获得。为简化计算，首先对失效率进行Bayes估计，再利用最小二乘法得到μ,σ2的参数估计。

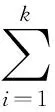
(tl,sl,rl),l=1,2,…,k,

(7)

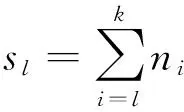
根据式(7)提供的信息有：

1)t=0时，失效概率p0=0;

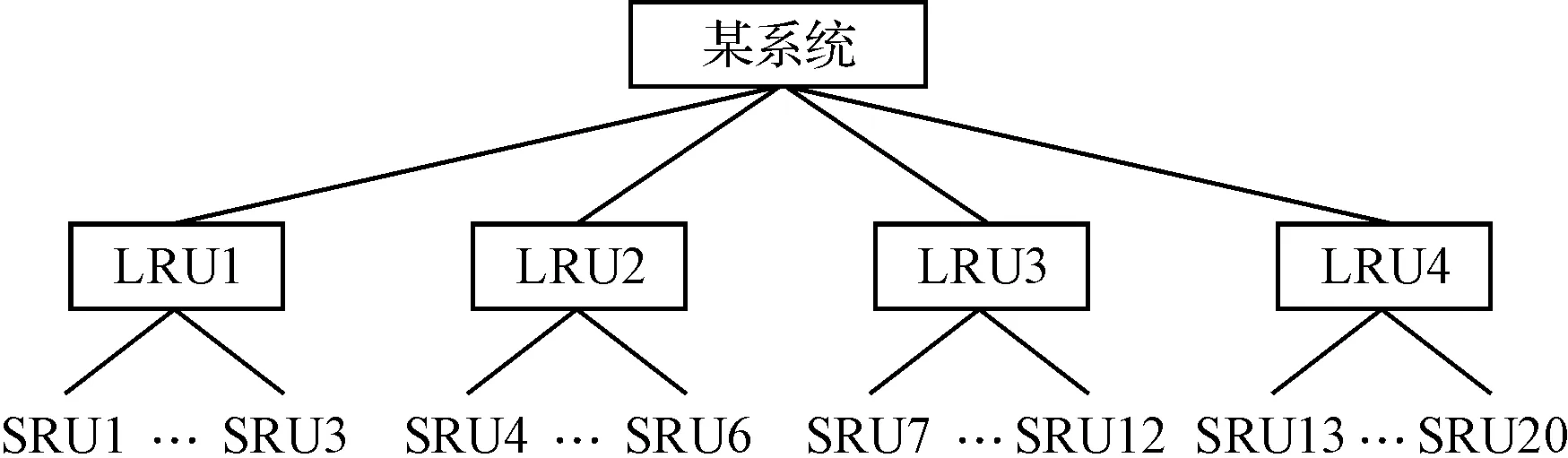
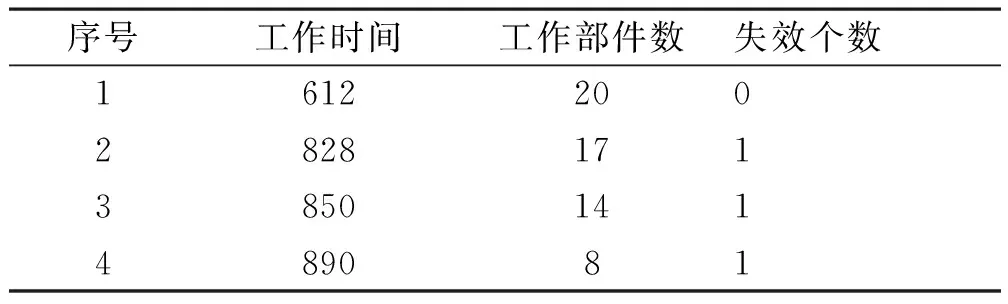
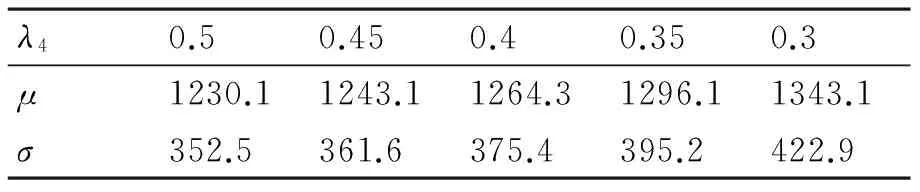
2) 由于t1≤t2≤…≤tk，记失效概率pi=P(T

p1

(8)

当sk较大时，pi(i=1,2，…,k)均较小。

由于在部件整个工作过程中只有一次失效，所以部件的失效率pi不会很大，当sk较大时，pi很小甚至接近于零。因此，部件在时刻tk前，可以认为失效率pk<0.5。通常pk的值可以通过专家经验给出比较精确的上界λk。此时pk的取值范围为(0,λk)，并且λk≤0.5[8]。

已知部件寿命T服从正态分布N(μ,σ2)，且

(9)

当t<μ时，上式大于零，即部件的正态分布函数F(t)是t的凹函数。则根据凹函数的性质有：

(10)

其中，t0

(11)

根据文献[8]可知，pi的Bayes估计分为如下两种情况：

(12)

i=m,m+1,…,k

(13)

由于已知部件寿命T服从正态分布N(μ,σ2)，则该部件在ti时刻的失效概率pi为

(14)

其中，Φ(∘)为标准正态分布函数。若Φ-1(·)表示为Φ(∘)的反函数，则上式可变化为

ti=μ+Φ-1(pi)σ,i=1,2,…,k

(15)

(16)

(17)

4算例分析

已知某部件寿命分布服从正态分布，且t～N(1385.7,3602)，在某系统中共有该部件20件，分别属于4型装备，其系统组成如图1所示。

图1　某系统结构组成图

通过查看该部件的使用情况记录，发现在该部件工作至828小时时有一个失效，各装备的工作情况如表1所示。

表1　各装备工作情况表

现对该部件的使用数据进行处理，运用Bayes估计方法对正态分布参数进行估计，并将估计值与真值进行比对，以验证该方法的可行性与准确性。

首先必须确定失效概率p4的上界λ4， 不妨取λ4=0.5，则计算得到正态分布参数的估计值为μ=1230.1,σ=352.5。其密度函数图如图2所示。从计算结果及密度函数图可以看出，Bayes估计计算得到的均值μ和方差σ均相当接近真值。

图2　Bayes估计计算所得参数值的密度函数图(正态分布)

1) 先验信息对计算结果的影响

通过改变λ4值来观察λ4取值对参数估计的影响，分别取0.45,0.4,0.35,0.3,0.2，计算得到的参数值如表2所示。

从表2可以看出，随着λ4值的变化，均值μ和方差σ的估计值变化不大，说明在λ4的取值较小时，其对均值μ和方差σ的估计值影响不大，即专家经验等先验信息的准确程度不会对Bayes估计的计算结果产生较大影响，也说明此方法计算得到的估计值是稳健、实用的。

表2　参数估计值

2) 失效部件数大于1时的处理方法

在分析装备的实际使用数据时，部件的失效个数可能不止一个，运用该Bayes估计方法只需要使用第一个失效部件发生的时间，并应将第二个失效部件发生的时间设定为任务结束时间，这样该方法就适应于失效部件数大于1的情况。在上例中，第二次故障发生时间为894.1小时，将任务结束时间t4取890小时，上例的计算结果即能证明该处理方法可行。

5结论

本文在极大似然估计和Bayes估计的一般计算方法基础上，结合装备使用数据给出了正态分布两种参数估计方法的计算流程，分别在一个失效数据和多个失效数据情况下，对Bayes估计方法的准确性进行了验证，说明了Bayes估计对正态分布部件参数估计的适用性。

参 考 文 献

[1] 刘天华.舰船装备备件需求确定与配置优化方法研究[D].武汉：海军工程大学，2012.

[2] 阮旻智.多级维修供应模式下舰船装备备件的配置优化方法研究[D].武汉：海军工程大学，2012.

[3] 单志伟.装备综合保障工程[M].北京：国防工业出版社，2008.

[4] 王自力.可靠性维修性保障性要求论证[M].北京：国防工业出版社，2011.

[5] 甘茂智，康建设，高崎.军用装备维修工程学(第2版)[M].北京：国防工业出版社，2010.

[6] 张志华.可靠性理论及工程应用[M].武汉：科学出版社，2012.

[7] Sanku D，Biswabrata P.Generalized inverted exponential distribution under hybrid censoring[J].Statistical Methodology，2014(18)：101-114.

[8] 张志华.正态分布场合下只有一个失效数据的统计分析[J].应用概率统计，1998，14(2)：185-190.

[9] 桂香，陈燕燕.正态分布在不同先验下的Bayes估计及风险比较[J].数学理论与应用，2007，27(2)：80-82.

[10] 茆诗松，程依明，濮晓龙.概率论与数理统计教程[M].北京：高等教育出版社，2011.

收稿日期：2016年1月7日,修回日期：2016年2月16日

作者简介：陆洪武，男，高级工程师，研究方向：装备综合保障。邵松世，男，博士研究生，工程师，研究方向：装备综合保障。

中图分类号

DOI：10.3969/j.issn.1672-9730.2016.07.035

Parameter Estimation Method for Normal Type Components

LU Hongwu1SHAO Songshi2

(1.Information System Agency of Department of Naval Equipment, Beijing100000)(2.Office of Research & Development, Naval University of Engineering, Wuhan430033)

AbstractFor the problem of the parameter estimation for normal type components, the calculation process of methods of maximum likelihood estimation and Bayes estimation is proposed according to the equipment data based on the general method of two parameter estimation. The accuracy of Bayes estimation and the influence of priori information on calculation results is analyzed with only one failure data, and the processing method is also researched with the multiple failure data. The accuracy and applicability of the Bayes estimation for the parameter estimation of normal components are illustrated by an example analysis.

Key Wordsnormal type components, maximum likelihood estimation, Bayes estimation, priori information, parameter estimation