基于二维Renyi熵与自适应人工鱼群算法的红外图像分割*

李晓峰　方　龙

(装甲兵学院　蚌埠　233050)



基于二维Renyi熵与自适应人工鱼群算法的红外图像分割*

李晓峰方龙

(装甲兵学院蚌埠233050)

摘要针对基于分解的二维renyi熵阈值分割算法中参数α的取值问题，根据均匀性测度评价指标，利用自适应人工鱼群搜索方法，提出一种α参数自适应选取方法。实验结果表明，本文所提出算法，针对不同红外图像均可以获得理想的图像分割效果，具有良好的通用性。同时还可以将算法计算复杂度由O(L6)降为O(L2)。

关键词红外图像; 分割; Renyi灰度熵; 自适应人工鱼群算法

Class NumberTP18

1引言

由于红外系统成像波长较长，目前又受限于制作工艺，导致产生的红外图像具有对比度低、非均匀性大、分辨率差、噪声大等缺陷。针对以上缺陷很多学者都进行了有针对性的研究：针对红外图像信噪比和对比度低的问题进行了图像增强研究；针对图像非均匀性问题进行了非均匀性校正研究；针对分辨率差进行了边缘检测研究。但以上方法对于复杂和多目标红外图像，存在着运算量大、处理效果不明显等缺陷，而采用图像分割可以较好地解决以上问题：它是将图像中感兴趣的目标提取出来的技术和过程，其作为图像分析、目标识别和图像理解的基础，可简化或改变图像表达形式，使图像更易被分析和理解。

本文针对红外图像对比度低、噪声大等特性，鉴于二维Renyi熵阈值分割法良好的分割效果和人工鱼群算法的全局搜索能力，提出一种基于自适应人工鱼群算法与二维Renyi熵相结合的红外图像分割算法，利用人工鱼群算法自适应地选取二维Renyi熵最佳阈值对应的参数α，并有效地将计算复杂度由O(L6)降至O(L2)。实验结果表明，针对红外图像特性，该算法在不增加运算时间的基础上，显示了良好的分割效果和抗噪性。

2二维Renyi熵阈值选取与参数优劣评估

2.1二维Renyi熵阈值选取

设图像具有L级灰度，则图像像素灰度集合Gx={0,1,…,L-1}，设窗口宽度为k，图像像素在k×k邻域内的平均灰度值也在L级内，图像的邻域平均灰度集合Gy={0,1,…,L-1}。对应一幅大小为M×N图像，f(x,y)表示图像中点(x,y)像素的灰度值，g(x,y)表示点(x,y)像素的邻域平均灰度值，则g(x,y)定义如下：

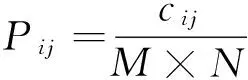
下面以标准图库中Lena图为例，如图1所示。图像所有像素中，目标区域和背景区域所占比例最大，且分布均匀。高峰主要出现在对角线附近，远离对角线区域峰值很小。

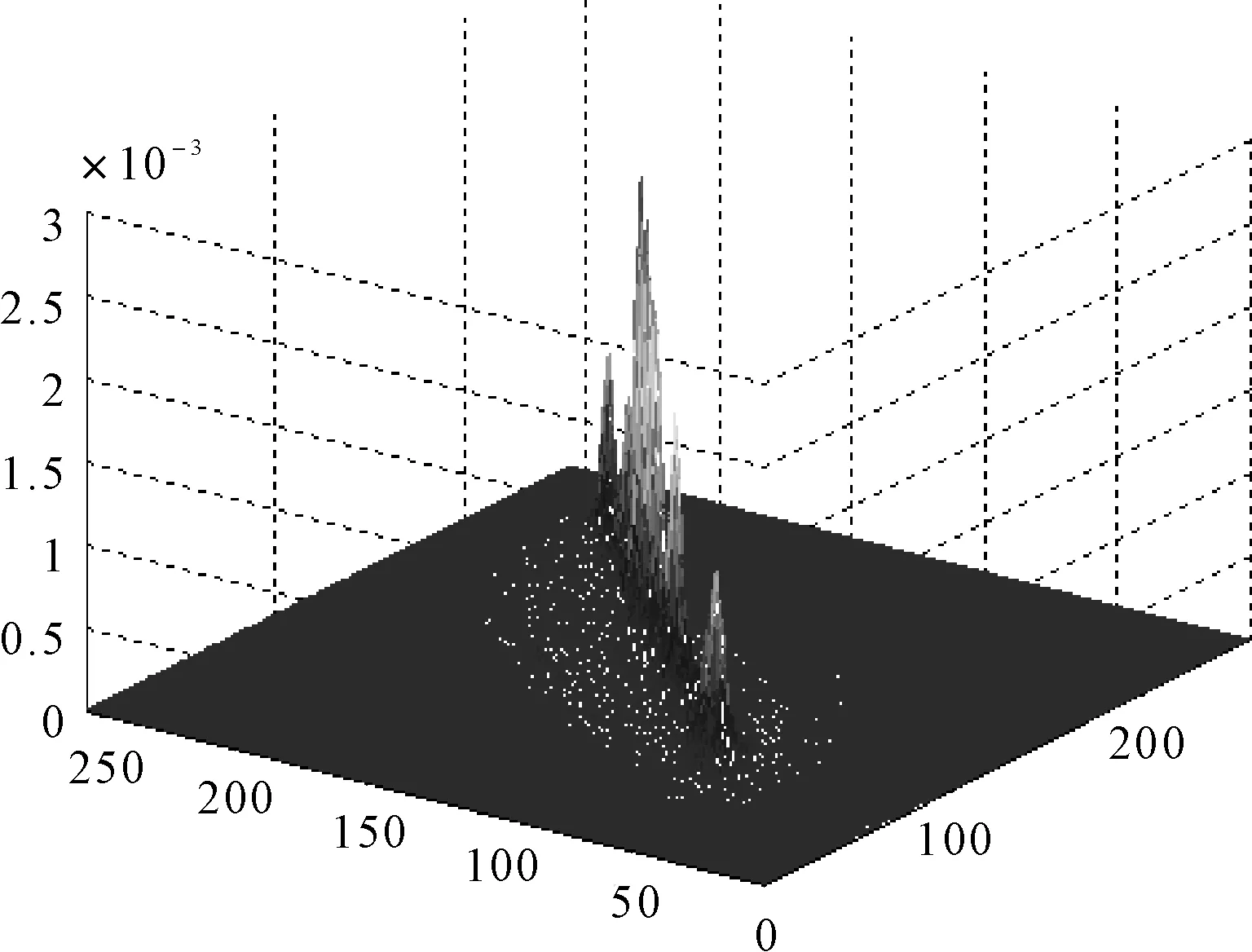
图1　Lena二维直方图

这时可设阈值元组(s,t)将二维直方图分割为四个区域，其中1区对应目标域，2区对应背景域，3区和4区分别对应边缘和噪声。根据Sahoo等提出的二维Renyi熵定义[1]，图像的总体二维Renyi熵为

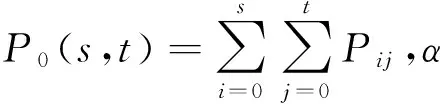
根据最大熵分割原理，当Hα(s,t)取得最大值的二元组(s,t)就是所求最佳阈值，这时最佳阈值向量(s*,t*)为

2.2均匀度测试参数评估

为了确定较优的参数值，本文采取基于图像分割评价准则的方法来自适应地获取较好的参数值，均匀性测度是用来评价分割方法性能的一个指标。对于一个区域，区域内的均匀性越好，其灰度分布越集中。假设在阈值(T，S)处对图像进行阈值分割，其均匀性测度可以按以下公式[2]表示：

式中i=1,2,Ri表示分割后的第i个区域，F(x,y)表示图像上坐标为(x,y)的像素点的灰度值，Ai表示区域Ri中的像素总个数，C是归一化参数。

则参数α的最优解可以表示为

α*=argmax{UM(α)},α>0

3自适应的人工鱼群算法

3.1基本人工鱼群算法

人工鱼群算法(Artificial Fish-Swarm Algorithm,AFSA)是一种模拟鱼群来寻求全局最优的新思路。它研究模拟鱼群的觅食、聚群和追尾等行为，通过每条人工鱼的局部寻优达到全局寻优[3]。作为一种新型寻优策略，该算法具有鲁棒性强、全局收敛性好、对初值敏感度小等优势。人工鱼群算法描述如下：

1) 觅食行为：指鱼循食物多的方向游动的一种行为，设人工鱼的当前状态为Ya，在其视野范围内随机选择一个状态Yb，数学表达式为

Yb=Ya+Visual.Rand()

其中函数Rand()产生0到1之间的随机数，Visual为视野范围。当食物浓度Xa>Xb时，向该方向前进一步，数学表达式为

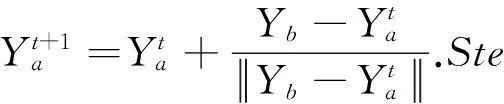
其中，Step为移动步长，如不满足前进条件，在其视野范围内再重新选择状态Yb，试探一定次数后，如仍不满足前进条件，则随机移动一步使得Ya到达一个新的状态。

2) 聚群行为：指每条鱼在游动过程中尽量向邻近鱼的中心移动以避免过分拥挤的一种寻优行为[4]。设人工鱼的当前状态为Ya，其邻域的伙伴数目nf，如果nf/N<δ，(0<δ<1)，表明伙伴中心有较多食物且不拥挤，则向中心位置Yc前进一步，这时Xa>Xc，数学表达式为

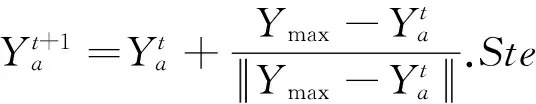
否则，执行其它行为。

3) 追尾行为：指鱼向其可视范围内的最优方向游动的一种行为。设人工鱼当前状态为Yi，探测其邻域内状态最优的邻居Ymax，如果Xa>Xmax，并且Ymax的邻域内伙伴数量nf满足nf/N<δ，(0<δ<1)，则表明Ymax附近有较多食物且不拥挤，则向Ymax方向前进一步，数学表达式为

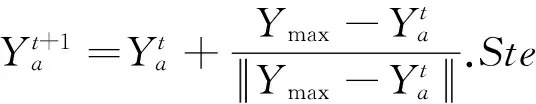
否则，执行觅食行为。

3.2改进的人工鱼群算法

通过对该算法深入分析后发现：虽然人工鱼群算法对初值要求不高、全局收敛性好、简单实现、在优化初期具有较快的收敛性等优点[5]，但其最大移动步长对该算法的收敛速度和求解精度会产生关键影响，随着步长的增大、移动速度的加快，算法初期收敛速度也随之加快，但当个体逐渐靠近最优点时，该算法存在着寻优精度变低、后期收敛速度变慢且不易跳出局部极值等不足；当步长变小时，虽然求解精度提高，但算法收敛也变得极其缓慢。

为解决以上问题，提出自适应的人工鱼群算法(Adaptive Artificial Fish-Swarm Algorithm，AAFSA)，主要是增加守候行为和重生机制以提高全体的协调性；伴随寻优从而动态地、自适应地调整鱼群参数和求解域。通过以上策略提高全局搜索能力、收敛速度和全局极值求解精度的目标。

4基于自适应的人工鱼群算法求解二维Renyi熵

为提高人工鱼群算法的收敛速度和求解精度，提出一种自适应人工鱼群算法AAFSA。具体作法：在算法初期，赋予每条人工鱼较大的步长，加快寻优速度，随着算法的进行，自适应地减小人工鱼的步长，从而加大算法的收敛速度，本文引入迭代函数Stepk+1=r*Stepk来自适应地减小人工鱼的步长。其中，k为当前迭代的代数，r∈(0,1)为衰减因子。

将自适应人工鱼群算法和基于分割的二维Renyi熵图像分割算法结合，自适应选取较优的参数值α。将图像经二维Renyi熵分割后的UM均匀度测试值作为目标函数。

具体算法步骤：

1) 初始化人工鱼群算法参数：初始化人工鱼群条数N，人工鱼群的初始位置，感知范围Visual，初始步长Step，拥挤度因子&，衰减因子r，最大尝试次数tryNumber，最大迭代次数T等参数[8]。

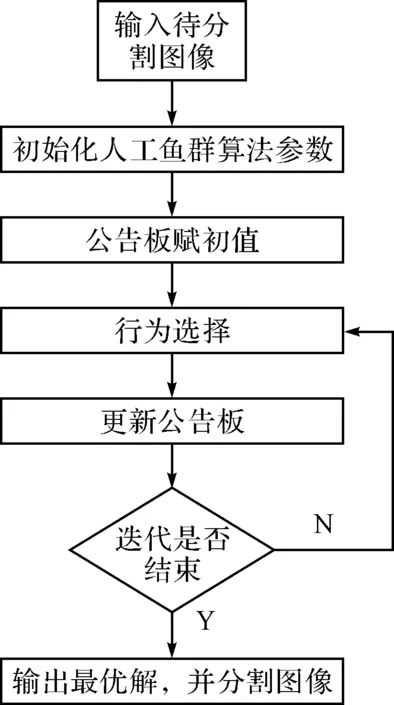
图2　算法流程图

2) 公告板赋初值：计算初始鱼群各条人工鱼的目标函数值并比较大小，取最优的人工鱼状态及其值赋给公告板。

3) 行为选择：各个人工鱼分别模拟追尾和聚群行为，通过比较目标函数值选择最佳行为来执行，缺省行为为觅食行为。

4) 更新公告板：每条人工鱼对自身的函数值和公告板的值进行比较，如优于公告板的值则取代之，否则公告板的值不变。

5) 判断迭代是否结束[9]：判断是否达到最大迭代次数T，达到则转至6),否则重复步骤3)～5)。

6) 输出最优解[10]。计算最优解α对应的图像I最佳划分阈值(s,t)max，并根据对应(s,t)max对图像I进行分割，得到分割后图像I′。

实验结果与分析：

经过多次实验，将人工鱼群算法的参数设计如下：人工鱼群条数N=20，人工鱼感知范围Visual=2.5，初始步长为Step=0.1, 衰减因子为r=0.95。拥挤度因子&=0.618，最大尝试次数tryNumber=6。

5仿真实验与结果分析

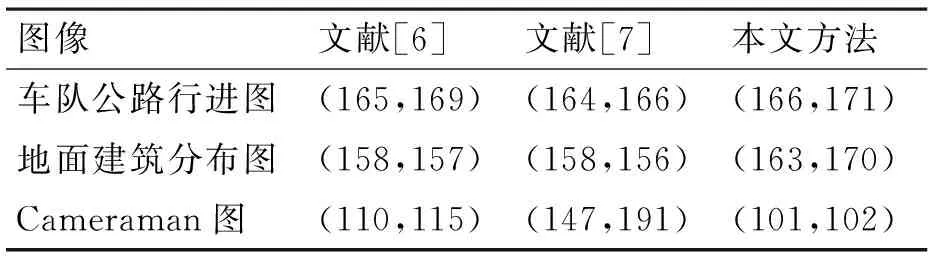
本文实验在系统配置：CPU 主频为i7-4770 3.4GHz，内存为4GB，Matlab 7.1下进行。为充分验证算法的有效性和鲁棒性，本文选取大量具有不同灰度分布的红外图像进行实验。实验包括：本文算法、基于分解的二维Renyi灰度熵[6](由文献[7]知，Renyi熵参数α的经验值为0.7，故实验中取α=0.7)、二维Renyi熵自适应阈值分割[7]的图像阈值分割在分割效果及时间上的比较。表1为阈值比较结果。

图3　车队公路行进图的分割效果

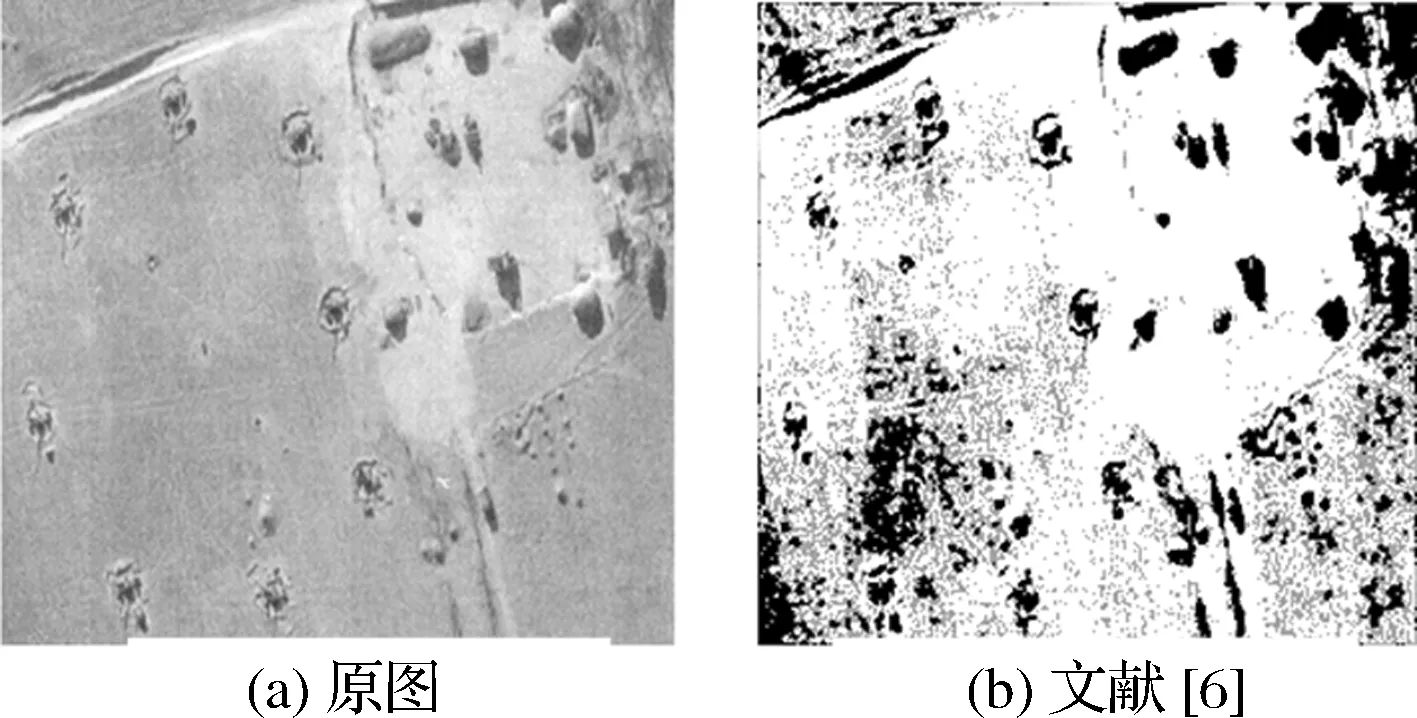
图4　地面建筑分布图的分割效果

图5　Camera图的分割效果

图像文献[6]文献[7]本文方法车队公路行进图(165,169)(164,166)(166,171)地面建筑分布图(158,157)(158,156)(163,170)Cameraman图(110,115)(147,191)(101,102)

表2　各算法运行时间比较(单位:s)

6结语

由仿真实验结果可以看出，不管是背景简单还是相对复杂的红外图像，本文所提方法都可以取得较好的分割效果，分割后的图像轮廓形状清晰明确、内部分布均匀。由于参数α的取值对Renyi熵阈值分割效果至关重要[11]，这时可由实验结果看出，文献[6]提出的基于分解的二维Renyi熵的分割方法，是把参数α取为0.7时对某些图像有较好的风格效果，但对其它图像还需要大量的实验才能找到合适的参数值；文献[7]提出的二维renyi熵中参数自适应选取的方法，虽然可以解决文献[6]中α需提前选取的问题，但运算时间长，且从实验结果看，分割效果不如文献[6]的分割方法；本文算法不仅解决了文献[6]中参数选择的问题，而且相比文献[7]，运算时间大幅缩短，分割效果也优于以上两种方法。

参 考 文 献

[1] Prasann Sahoo, Gurdial Arora. A Thresholding Method Based on Two-dinmensional Renyi’s Entropy [J]. Pattern Recognition,2004,37:1149-1160.

[2] LUXBURG U V. A tutorial on spectral clustering [J]. Statistics and Computing,2007,17(4):395-416.

[3] 李晓磊.一种新型的智能优化方法—人工鱼群算法[D].杭州：浙江大学,2003:20-53.

[4] NG A Y, JORDAN M I, WEISS Y. On spectral clustering: analysis and an algorithm[C]//Proceedings of the 14th Advances in Neural Information Processing Systems (NIPS 2001),Vancouver, British Columbia, Canada,2002:849-856.

[5] CRISTIANINI N, SHAWE-TAYLOR J, KANDOLA J. Spectral kernel methods for clustering[C]//Proceedings of the 13th Advances in Neural Information Processing Systems (NIPS 2001), Vancouver, British Columbia, Canada,2001:649-655.

[6] 龚劬,王菲菲.基于分解的二维Renyi灰度熵的图像值分割[J].计算机工程与应用,2013,49(1):181-185.

[7] 雷博，范九伦.二维Renyi熵阈值分割方法中参数的自适应选取[J].计算机工程与应用,2010,46(22):16-19.

[8] 曲良东.基于自我调整高斯变异的人工鱼群算法[J].计算机工程,2009,35(15):182-189.

[9] 范玉军.改进的人工鱼群算法[J].重庆师范大学学报:自然科学版,2007,24(3):23-26.

[10] 曲良东.混合变异算子的人工鱼群算法[J].计算机工程与应用,2008,44(35):50-52.

[11] 段其昌.粒子群优化鱼群算法仿真分析[J].控制与决策,2013,28(9):1436-1440.

收稿日期：2016年1月12日,修回日期：2016年2月22日

作者简介：李晓峰,男,硕士,助教,研究方向：军事情报学。方龙,男,硕士,副教授,研究方向：计算机工程。

中图分类号TP18

DOI：10.3969/j.issn.1672-9730.2016.07.027

Infrared Image Segmentation Based on AAFSA and 2D-Renyi Entropy Threshold Selection

LI XiaofengFANG Long

(Armored Force Institute, Bengbu233050)

AbstractTo select optimal parameter a in decomposed 2D-renyi entropy image threshold segmentation method, a new adaptive method according to the uniformity measure which is an image segmentation evaluation criteria is proposed based on adaptive artificial fish-swarm algorithm. Experiment results show that the method can get desired segmentation result for each image. The algorithm is of universality and can also reduce the computational complexity from O(L6) to O(L2).

Key Wordsimage segmentation, decomposition, Renyi entropy, adaptive artificial fish-warm algorithm